Возможности различных методов автоматического распознавания стадий сна
Автор: Антипов О.И., Захаров А.В., Повереннова И.Е., Неганов В.А., Ерофеев А.Е.
Журнал: Саратовский научно-медицинский журнал @ssmj
Рубрика: История медицины, юбилейные даты
Статья в выпуске: 2 т.8, 2012 года.
Бесплатный доступ
Цель: рассмотреть информативность применения различных фрактальных методов детерминированного хаоса к автоматизированному распознанию фаз сна по компьютерным электроэнцефалограммам (ЭЭГ). Методы. Использован метод нормированного размаха Хёрста, метод расчета корреляционного интеграла Грассбер-гера — Прокаччиа и метод аппроксимационной энтропии. Результаты. Показано, что, используя данные методы, при соответствующем подборе параметров самих методов, с помощью необходимой нормировки исходных данных и усреднения результатов можно получить гипнограмму, имеющую полное совпадение определяемых фаз сна для половины эпох, регистрируемых на ЭЭГ. Заключение. Современные методики автоматического распознавания стадий сна на основе детерминированного хаоса позволяют значительно сократить время интерпретации полисомнографической записи и уменьшить количество каналов, по которым производится регистрация параметров сна.
Детерминированный хаос, полисомнография, электроэнцефалография
Короткий адрес: https://sciup.org/14917535
IDR: 14917535
Текст научной статьи Возможности различных методов автоматического распознавания стадий сна
1Введение. Состояние сна является неотъемлемой частью человеческого существования, и его расстройства отражаются на всех сферах деятельности человека — социальной и физической активности, познавательной деятельности и др. [1]. Сон занимает более трети времени человеческой жизни. Физиологически сон неоднороден и имеет характерную структуру [2]. Он включает в себя различные функциональные состояния — фазы и стадии, чередующиеся в определенной последовательности и образующие циклы сна. Нарушение естественных циклов сна является признаком расстройств сна, которые, в свою очередь, могут иметь серьезные негативные последствия для организма, такие, как сниженная работоспособность, утомляемость, нарушения деятельности сердечно-сосудистой и центральной нервной систем. Своевременное диагностирование расстройств сна может выявить и предупредить развитие многих серьезных заболеваний. Во время сна могут зарождаться или, наоборот, облегчаться многие патологические процессы, поэтому в последние годы значительное развитие получила медицина сна, изучающая особенности патогенеза, клиники и лечения патологических состояний, возникающих в период сна и оказывающих значительное влияние на функционирование организма в дневное время.
Такая патология, как инсомния, является самым распространенным нарушением сна. В популяции инсомния встречается в 13-65%, а для 12-22% людей является клинической проблемой. Для объективного изучения сна и его нарушений используется полисомнография — метод, включающий параллельную регистрацию электрофизиологических сигналов, таких, как электроэнцефалограмма (ЭЭГ), электрооку-лограмма (ЭОГ) и электромиограмма (ЭМГ).
Общепринятая система классификации стадий сна была разработана Рехчаффеном и Кейлсом в 1968 г. Согласно данному методу, эксперт вручную анализирует записи электрофизиологических параметров, длительность которых в среднем составляет 8 часов. Для каждого тридцатисекундного отрезка записи последовательно рассчитываются характеристики, на основании которых принимается решение об отнесении рассматриваемого участка к той или иной стадии сна. Метод построения гипнограмм по правилам Рехчаффена и Кейлса является до сих пор наиболее распространенным и общепринятым, однако он имеет ряд существенных ограничений, а именно: высокая трудоемкость и субъективность оценки, что приводит порой к значительным расхождениям показателей одной и той же гипнограммы при расшифровке двумя разными специалистами. Допустимый предел расхождения на данный момент принято считать не более 20% в 8-часовой записи. Поэтому в настоящее время существует необходимость в разработке объективных автоматизированных методов распознавания стадий сна, которые в совокупности с прибором для регистрации электрофизиологических сигналов образуют систему для доступной диагностики расстройств сна.
Данная задача решалась отдельными авторами [3, 4], однако фрактальные меры детерминированного хаоса использовались ими только лишь для сегментации ЭЭГ на стационарные участки по методу расчета фрактальной размерности Хигучи [5, 6, 7]. Сама же задача распознания стадий сна решалась с помощью исследования фаз сна по ЭЭГ человека на основе скрытых моделей Маркова [5, 8].
Цель: определение стадий сна по фрактальному анализу биоэлектрической активности, регистрируемой по ЭЭГ-каналу.
Методы. Метод нормированного размаха Хёрста и его применение к расчету временной выборки ЭЭГ-сигнала. На первом этапе расчета показателя Хёрста находится среднее значение напряжения U N за N временных отсчетов:
N
< U > N = м £ U ( n > N n = 1
Тогда накопившееся отклонение и ( n ) от его среднего значения U N определяется суммой:
n
X ( n , N ) = £ { U ( p ) - U N }.
p = 1
Размах отклонений определятся как
R ( N ) = max X ( n , N ) - min X ( n, N ). 1 < n < N 1 < n < N
Стандартное отклонение можно вычислить по формуле квадратного корня из дисперсии:
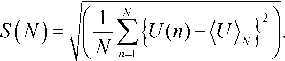
Адрес: 443095, г. Самара, ул. Ташкентская, 220, кв. 141.
Тел.: +79171620301.
Как показано в работах Хёрста, для большинства временных рядов наблюдаемый нормированный размах RS описывается эмпирическим соотношением [9]:
RIS = (aN)H, где H — показатель Хёрста, α — произвольная постоянная. Cледует отметить, что размах называется нормированным, поскольку он должен быть разделен на квадратный корень из дисперсии.
Метод восстановления фазового пространства и теорема Такенса. Данный метод восстановления фазового пространства системы был предложен Такен-сом. Идея метода состоит в следующем. Любая динамическая система должна через некоторое конечное время принимать положениея, сколь угодно близкое к исходному, о чем говорит известная теорема Пуанкаре [11]. Среднее время возврата т , или цикл Пуанкаре, определяется формулой, предложенной Смолуховским:
да да
Т = t T kP. T Pk k=1 / k=1 ’ где Pk — вероятность возврата системы в исходную область за время kt.
Известно, что величина цикла Пуанкаре для систем из большого числа частиц огромна. Однако стохастическое поведение может возникать и в системе, состоящей всего из нескольких степеней свободы; в этом случае время возврата доступно для наблюдения и оценки.
Наличие в системе некоего цикла позволяет при исследовании поступить так же, как и в радиотехнике при обработке узкополосного сигнала, — сдвинуть измеренную последовательность относительно себя на «половину периода». «Периодом» в данном случае является оцененное значение среднего времени возврата т .
По теореме Такенса (10) можно вычислить корреляционный интеграл (о котором речь пойдет далее) и фрактальную размерность по измерениям временной последовательности лишь одной составляющей. Следуя Такенсу, необходимо сконструировать пространство вложения (или псевдофазовое пространство) с m -мерным вектором по значениям одной физической переменной, взятым со сдвигом т :
X i = X ( t) = { x ( t i ),x ( t -т ),..., x ( t - (m - 1) т ) } .
Метод Грассбергера — Прокаччиа для вычисления корреляционного интеграла. С помощью описанного метода задержек сформируем из исследуемого ряда аттракторы в m -мерных псевдофазовых пространствах для m =1, 2, 3, … Далее, для каждого аттрактора в пространстве m рассчитаем корреляционный интеграл по формуле:
-
1 N N
Ce(e,N) = Nm NN^TT6(e -|x -xj), i * j , где N — количество точек аттрактора, |xi–xj| — абсолютное расстояние между i-ой и j-ой точками аттрактора в m — мерном пространстве, f — размер разрешающей ячейки, i(∙) — функция Хевисайда. По сути говоря, Ce(f,N) — зависимость количества точек аттрактора в m-мерном пространстве, расстояние между которыми Г d 1g Ce (e, N) DC = lim lim —-—---- e^o N ^да ^ d ig e . Данный алгоритм вычисления Dc связан с тем, что при сравнительно малых значениях f должен соблюдаться степенной закон: Ce(e, N) - eDC , где Dc — корреляционная размерность. Поскольку корреляционная размерность идет под индексом q=2 в спектре Реньи, то она является нижней оценкой размерности Хаусдорфа — Безиковича (которая идет под индексом q=0), так как спектр Реньи является ниспадающим с ростом индекса q. На полученном графике ищут точку, когда зависимость Dc (m) достигнет насыщения. Значение m точки насыщения будет соответствовать независимой оценке размерности пространства вложения, а значение Dc будет соответствовать корреляционной размерности исследуемого псевдофазового аттрактора восстановленного из исследуемого ряда. Согласно теореме Такенса, эти характеристики отражают соответствующие значения динамической системы, породившей исследуемый ряд. Теоретически точка насыщения является таковой, если полученное значение корреляционной размерности Dc не будет меняться вплоть до m=int [2Dc] +1 (здесь операция int [∙] подразумевает округление в большую сторону). Соблюдение данного условия гарантирует надежность полученного результата. Аппроксимационная энтропия. Аппроксимационная энтропия является мерой детерминированного хаоса и предназначена для получения информации о сложности процессов, происходящих в системе на основании коротких временных рядов X= [x (1), x (2), …, x (N), где N — длина исследуемого ряда и составляет примерно от 75 до 5000 отсчетов. Значение аппроксимационной энтропии зависит от размерности псевдофазового пространства m, которое строится по методу Такенса, «фактора фильтрации» r и длины исследуемого ряда N, и определяется из выражения: ApEn (m, r, N) = Ф m (r) - Ф m+1 (r). Здесь Фm (r) и Фm+1(r) определяются из выражений: N - m фm (r)=-ТГ T in (Cm (r)), N - m 11 v ' N - m фm+1( r) =, T in (Cm+1( r)). N - m ■‘"7 Как и для корреляционного интеграла, с,”(r) и C,m+l(r) определяются суммами: N-m+1 C” (r) = IT"" 2 *(r - X-) - x(j)) N - m +1 ’ N - m C-+1(r) = Tv----2 ^(r - Xi) - x(j)|) N - m j1 . В результате определение аппроксимационной энтропии может быть сведено к получению значения ApEn с помощью общего выражения [14]: ApEn (m, r, N) = N - m N - m 2 in i=1 ( C” (r))' I Cm+1(r) j с соответствующим вычислением значений C”(r) и с,”+l(r) для каждого -. Результаты и их обсуждение. Для реализации вычислений на компьютере была разработана программа с использованием среды Borland C++ Builder. В результате применения всех перечисленных методов было установлено, что при анализе только лишь одного канала ЭЭГ выявить парадоксальную стадию сна нельзя. Это связано с тем, что значения всех без исключения фрактальных мер, используемых в работе, для фазы с быстрыми движениями глаз (БДГ) совпадают со значениями для поверхностного сна и для фазы расслабленного бодрствования (РБ), причем между собой I и II стадии сна, а также фаза РБ хорошо дифференцируются. Поэтому, поскольку в данной работе для автоматизированного распознания фаз сна ставилась цель анализировать только один канал ЭЭГ, было решено проигнорировать наличие фазы с БДГ. Это привело к тому, что на результирующей гипнограмме фаза с БДГ распознавалась программой либо как фаза РБ, либо как I или II стадия сна. В данной работе также не производилось распознавание фаз времени движения (ВД), вызванных двигательными артефактами. Гипнограммы, полученные с помощью всех трех используемых в данной работе методов, представлены на рис. 1 в виде пунктирных линий. Гипнограмма, сформированная «вручную» специалистами по ЭЭГ, показана на этом же рисунке в виде сплошной линии. По оси абсцисс отложены номера эпох со времени начала регистрации ЭЭГ. По оси ординат отложены следующие фазы: ВД — время движения (нераспознаваемая фаза, связанная с наличием двигательных артефактов, длительность которых составляет минимум 25% времени эпохи), РБ — расслабленное бодрствование, БДГ — фаза с быстрым движением глаз (фаза парадоксального сна), I, II, II, IV — 1, 2, 3 и 4-я фазы сна соответственно. Как видно из полученных результатов, использование всех трех методов позволило оценить общую картину сна, поскольку четко дифференцированы фазы глубокого дельта-сна и выход в фазу РБ. Распознание поверхностных стадий сна, как видно из рисунка, осложнено только лишь отсутствием выделения фазы парадоксального сна. Количественные в) Рис. 1. Гипнограммы, полученные специалистами по ЭЭГ (сплошная линия) и гипнограммамы, полученные с помощью следующих фрактальных методов детерминированного хаоса (пунктирные линии): а — методом нормированного размаха Хёрста; б — методом Грассбергера — Прокаччиа; в — методом аппроксимационной энтропии характеристики совпадения гипнограмм, полученных с помощью различных методов, используемых в программе и гипнограммы, составленной специалистами вручную, представлены в таблице. Количественная оценка совпадения гипнограмм, полученных различными фрактальными методами, с гипнограммой, полученной специалистами Используемый метод Количество эпох, имеющих полное совпадение фаз сна, % Нормированный размах Хёрста 52,2 Корреляционный интеграл Грассбергера — Прокаччиа 47,8 Аппроксимационная энтропия 48,5 Если сравнивать затраченное время вычисления, то использование метода нормированного размаха Хёрста позволило получить результаты на два порядка быстрее, чем использование метода аппроксимационной энтропии, и на три порядка раз быстрее, чем вычисление методом Грассбергера– Прокаччиа. Заключение. В результате проведенного исследования показано, что путем использования фрактальных мер детерминированного хаоса без дополнительного выявления парадоксальной стадии сна, анализируя только лишь один сигнал ЭЭГ, можно получить гипнограмму, имеющую полное совпадение определяемых фаз сна для половины регистрируемых эпох. При этом фаза с БДГ распознавалась программой либо как фаза РБ, либо как одна из фаз поверхностного сна (I и II стадии). Данный результат был получен для всех используемых в работе методов, причем без отсеивания фаз, содержащих двигательные артефакты. Самая высокая скорость вычислений достигалась с помощью метода нормированного размаха Хёрста, имеющего максимальное совпадение фаз сна при сравнении автоматического и ручного обсчета гипнограмм. Важно, что результаты вычислений данными методами наиболее точно совпали с результатами, полученными «вручную» специалистами по ЭЭГ. Данный метод достаточно эффективно показал себя при интерпретации гипнограмм пациентов, страдающих хронической инсомнией, заболеванием, при котором наблюдается наиболее выраженная депривация медленного сна при относительной сохранности быстрого сна. Методика позволяет эффективно и с наименьшими затратами проводить оценку выраженности объективных показателей инсомнии, а также оценивать эффективность назначаемой при данном заболевании терапии.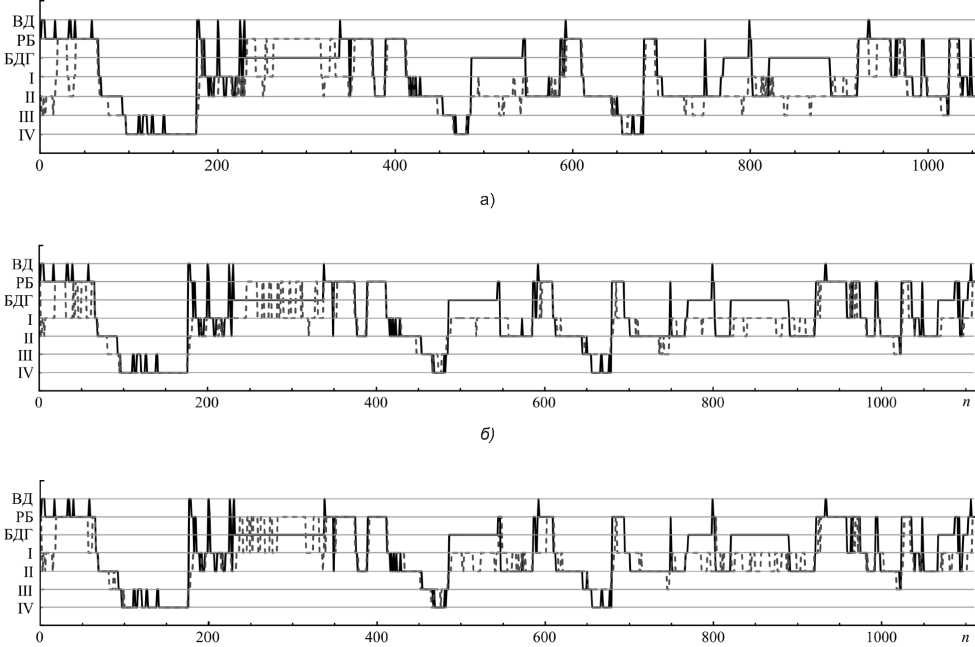
Список литературы Возможности различных методов автоматического распознавания стадий сна
- Левин Я. И. Сомнология: сон, его cтруктура и функции инсомния//Рос. мед. журн. 2007. Т. 15, № 15. С. 11 -30
- Неврология: нац. рук-во/Е. И. Гусев, А. Н. Коновалов, В. И. Скворцова, А. Б. Гехт, М.: ГЭОТАР-Медиа, 2009. 1035 c.
- Дорошенков Л. Г. Методы и алгоритмы обработки электрофизиологических сигналов для автоматического распознавания стадий сна: автореф. дис. … канд. техн. наук. М., 2009
- Хакен Г. Принципы работы головного мозга: синерге-тичнский подход к активности мозга, поведению и когнитив-ности деятельности. М.: ПЕР СЭ, 2001. 351 с.
- Дорошенков Л. Г., Гендель И. Г. Сегментация ЭЭГ на стационарные участки по методу расчета фрактальной размерности Хигучи//XV Всероссийская межвузовская НТК студентов и аспирантов «Микроэлектроника и информатика -2008»: тез. док. М.: МИЭТ, 2008. С. 259
- Дорошенков Л. Г., Конышев В. А., Селищев C. B. Исследование фаз сна по ЭЭГ человека на основе скрытых моделей Маркова//Медицинская техника. -2007. № 1. С. 24 -28
- Рюэль Д., Такенс Ф. Странные аттракторы. М., 1981. С. 117 -151
- Брур Х. В., Дюмортье Ф., Стрин С. ван, Такенс Ф. Структуры в динамике: конечномерные динамические системы/пер. с англ. под ред. Л. М. Лермана. М., 2003
- Федер Е. Фракталы/пер. с англ. М.: Мир, 1991. 254 с.
- Takens F. Detecting Strange Attractors in Turbulence//Dynamical Systems and Turbulence: Lecture Notes in Mathematics. Berlin., 1981. Vol. 898. P. 366 -381.


