Возможности теории графа в электрических системах

Составление уравнений состояния для сложных электрических систем является весьма трудоемкой процедурой, поэтому решение данной задачи целесообразно возложитъ на компьютер. Для этого требуется иметъ формализованный подход к составлению уравнений, который был бы одинаков для схем любой сложности и конфигурации. Такой подход можетъ бытъ разработан на основе аналитического представления конфигурации схемы замещения с помощью элементов теории графов и алгебры матриц.

Конфигурацию схемы замещения электрической системы можно отобразить в виде графа. Граф представляет собой множество вершин (узлов) и ребер (ветвей), соединяющих некоторые (а может быть и все) пары вершин. При изображении схем в виде графов нет надобности в специальных обозначениях сопротивлений и ЭДС. Ветви графически изображаются (прямой или кривой) с указанием их направлений. Таким образом, направление ветви от начального узла к конечному узлу одновременно является положительным направлением и для всех участвующих величин - ЭДС, тока и падения напряжения. Любая из этих величин может получиться положительной или отрицательной по отношению к принятому направлению.

Для иллюстрации вышесказанного рассмотрим следующую электрическую схему:

D рис.1

На рис 2. данная схема показана в виде связанного направленного графа на которой выбраны направления ветвей, а также указаны номера ветвей и узлов.

рис.2

Для     направленного

показанного

графа, Выбрав узел d в качестве балансирующего, получим матрицу рис. 2, матрица M имет вид:

M из M путем исклю-чения

+ 1

- 1

Mz

-

+ 1

- 1

+ 1

- 1

0 a

последней строки:

0    + 1

+ 1 b

+ 1

- 1

- 1

+ 1

— 1

c

0 d

M = 0  0

— 1   0

0   0

— 1   0

+ 1

— 1

узлы

1    2   3   4   5    6

ветви

Известно, что одной и той же электрической цепи в общем случае соответствует несколько различных систем независимых контуров, или, иными словами, одной и той же матрице M - можно поставить в соответствие несколько матриц N. Однозначность в выделении системы независимых контуров, позволяющая получить матрицу N по матрице M , может быть достигнута при использовании таких понятий теории графов, как дерево и хорды. Деревом называется наименьший связанной подграф, содержещий все вершины графа. Иными словами, дерево – это разомкнутая часть замкнутой схемы, которая соединяет все ее узлы. Ветви, не вошедшие в дерево схемы, называются хордами. Одна и та же схема может быть разделена на дерево и хорды по-разному. На рис.3 показаны некоторые варианты возможные случаи разделения графа, изображенного на рис.2, соответственно на дерево и хорды.

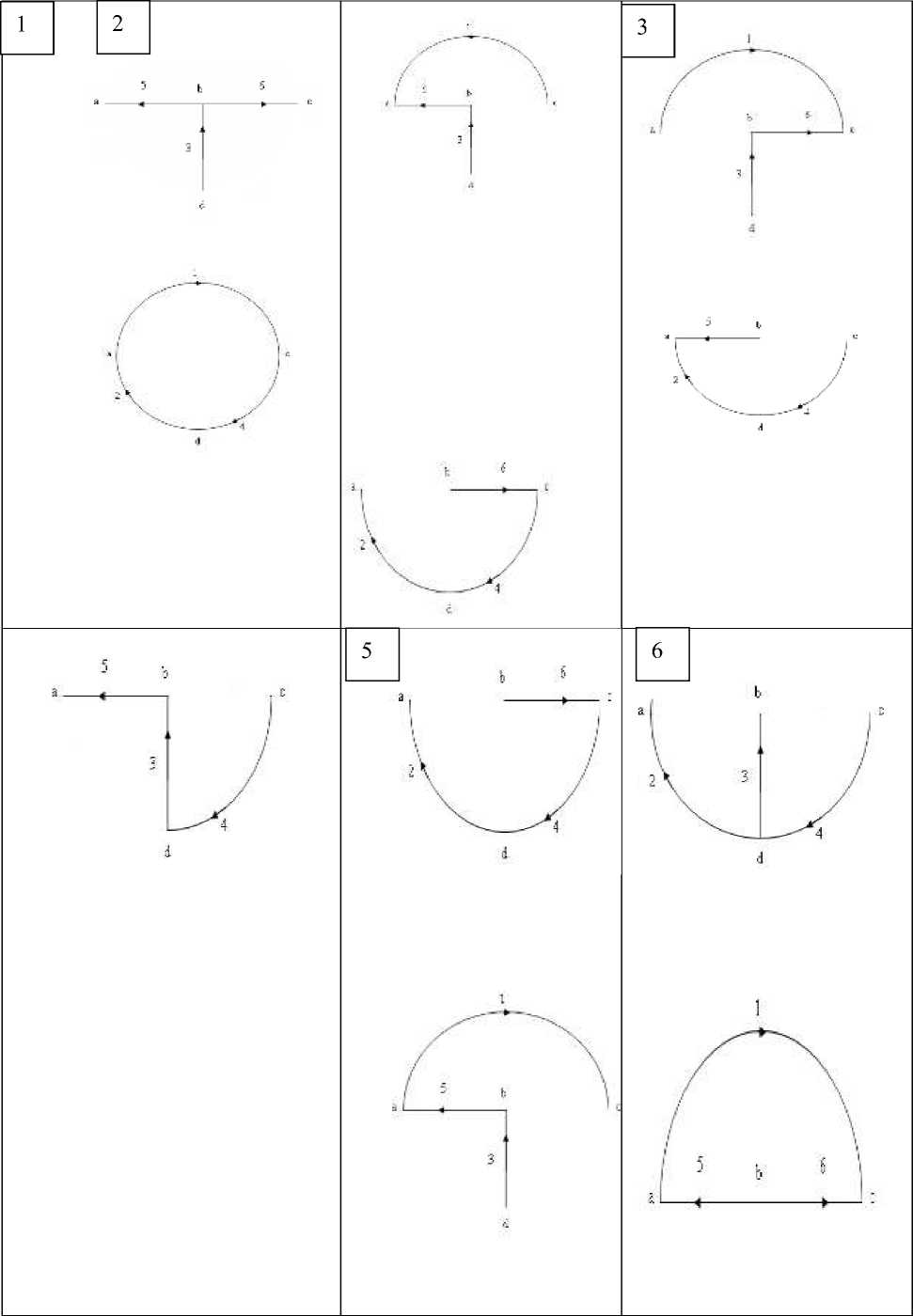
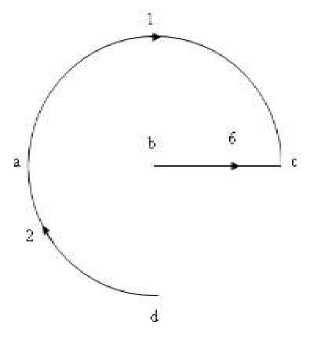
В итоге матрице M , записанная первоначального при произвольной нумерации ветвей, путем перестановки столбцов преобразуется к виду.

M = [ M _a M e ]

где M - подматрица (блок), относящаяся к дереву схемы, M - подматрица, характери-зующая подграф, состоящий из хорд.

Разделив матрица M на блоки, соответстующие дереву и хордам графа, однозначно определим матрица N для системы базисных контуров, отвечающих данному дереву.

N = [ N . N_P ],     N a =- M TT " MT;  N e = 1

Матрица M и N (матрица соединений ветвей в узлах (первая матрица инциденций) и матрица соеденинений ветвей в независимые контуры (вторая матрица инциденций)) дают возможность записать уравнения состояния электрической цепи (узловых или контурных уравнений) в матричной форме [1].

Преобразуя уравнения состояния электрической цепи (узловых или контурных уравнений) в матричной форме, при вычислении электрических схем, операции над матрицами (Вид ^ Панели инструментов ^ Матрицы) и решения СЛАУ возложим на МathCAD.

Пакетные программы, с помощью которых появилась возможность решения математических задач (в том числе и других задач науки, описывающее такими же математическими моделями) без составления компьютерных программ [2]. В учебном процессе (иногда и в научных учреждениях) с помощью использования таких систем как MathCAD, Maple, Matlab, Mathematika и.т.д занятия становятся интереснее, осмысление содержания занятия более быстрое и глубокое а также на укрепление излагаемых понятий и на решение задач остаётся достаточно много времени. Из выше указанных систем, MathCAD - более проще чем остальные и она предназначена для технических вузов, а остальные, можно сказать, для профессиональных математиков. Именно в MathCAD задача формулируется в наиболее естественном математическом виде, а в других математических системах шаги алгоритма решения задачи записываются с помощью команд системы.