Возможностно-темпоральной модели данных PTDM по сравнению с другими моделями хранения и обработки нечеткой темпоральной информации

Применение компьютерного инструментария предсказательной аналитики является важнейшим фактором развития и конкурентного преимущества предприятий в условиях рыночных отношений и коммерциализации информации. Формирование новых аналитических запросов, основанных на решении задач обработки сложно-структурированных данных, выявления динамики их изменения и сегментации с учетом временной неопределенности привели к появлению математических моделей и алгоритмов обработки нечетких темпоральных данных. С развитием технологий построения предсказательной аналитики системы стали предъявлять требования к унификации применения вычислительных алгоритмов через создание специализированных программных библиотек и веб-сервисов. В настоящее время не существует завершенных или стандартизованных программных алгоритмов, выполняющих обработку нечетко-темпоральных данных. Наличие таких алгоритмов позволит системам обрабатывать сложно-интерпретированные запросы, направленные на повышение эффективности при аналитике результатов обработки нечетких временных данных. Ввиду этого была поставлена задача проведения анализа существующих моделей хранения и обработки нечеткой темпоральной информации и выявления отличительных характеристик разработанной возможностно-темпоральной модели данных PTDM. Для этого требуется представить различные направления реализации темпоральных моделей хранения данных, определить основные понятия темпоральных элементов, привести примеры их использования, провести анализ подходов, использующих теорию нечетких множеств в описании темпоральных структур данных.

Интервальная алгебра Аллена

Выделим одну из наиболее распространенных моделей интервальных отношений – темпоральную алгебру Дж. Ф. Аллена [1], которая включает в себя 13 отношений, существующих между двумя временными интервалами (таблица 1).

Интервальная алгебра Аллена рассматривает только классические темпоральные отношения временных показателей без возможности определения нечетко-темпоральной структуры, а также без поддержки алгоритмов обработки нечеткотемпоральных данных. Также темпоральная алгебра Аллена не рассматривает отношения точек между собой, а также отношения интервалов и точек.

Модель FTRM

Модель FTRM (fuzzy termporal relational model) [2] расширяет реляционную модель путем моделирования времени и нечеткости в данных. Можно определить различные виды неточностей: неточности в степени принадлежности самой

Таблица 1. Темпоральная алгебра Дж. Ф. Аллена

Наименование отношения Интервалы I и J Визуализация Перед (Before) I перед J Ei< S 1                      J -►t После (After) I после J Si> E J                      1 -►t Равен (Equal) I равен J Si= j Ei= E J -►t Встречает (Meets) I встречает J Ei= S -L- j -►t Встречен (Met by) I встречен J Si= E, —i -►t Пересекает (Overlaps) I пересекает J Si< j Ei< Ej Л Ei> Sj -L- j -► Пересечен (Overlapped by) I пересечен J Si> S' Ei> Ej л Si< Ej —i -►t В течение (During) I в течение J Si> S. Ei< Ej -►t Содержит (Contains) I содержит J Si< SJЛ Ei> Ej J                 i -►t Начинает (Starts) I начинает J Si= SJЛ Ei< Ej I ______________________J -►t Начат (Started by) I начат J Si= SJЛ Ei> Ej J -►t Завершает (Finishes) I завершает J Si> SJЛ Ei= Ej -►t Завершен (Finished by) I завершен J Si< SJЛ Ei= Ej J 1________________________________________________________________ -►t сущности, неточность в сущности базового типа и ее сущностях подтипа, неточность в кортежах отношения, неточность на уровне атрибута и неточность значений, связанных с типом атрибута.

Структура множества Время определена как T , < > , где T - некоторое исчисляемое множество и «<» – линейный порядок на множестве T , т. е. для любых 1 1 и 1 2 применимо 1 1 = 1 2 , 1 1 <  t 2 или 1 1 >  1 2 . В данной модели время рассматривается как дискретное и изоморфное к естественным числам, поскольку любая предметная область, которая может быть определена для атрибутов времени предлагаемой модели, может иметь бесконечное множество наименований для временных моментов или временных интервалов. Для определения темпоральной модели принят подход, определяющий время для каждого кортежа.

Предлагаемая модель данных состоит из трех основных конструкций: сущности (темпоральной или нетемпоральной), атрибутов (изменяющихся, не изменяющихся во времени и частично изменяющихся во времени) и нечетких атрибутов. Ограничения, обеспечивающие консистенцию данной схемы:

• •    Использование дат начала и завершения активации вместо времени действительности, ввиду наличия во второй большого количества типов, что создает сложность при определении сущности.

• •    Представление временных фактов как в моментах времени, так и на интервалах.

• •    Введено время обновления вместо времени транзакции. Обновление относится к изменению данных (кортежа) любого вида (insert, delete или изменение).

• •    Время активации может быть представлено в различной гранулярности: год, месяц, неделя, день, час, минута, секунда и т. д. Преобразование из одной гранулярности в другую осуществляется функцией конвертации.

  Таблица 2. Нечеткое темпоральное отношение с состояниями объектов

  ID	Дата начала	Дата завершения	Время обновления	Состояние
  1	01-12-2021	03-12-2021	01-12-2021	Очень высокое
  2	31-11-2021	03-12-2021	31-11-2021	Высокое
  3	12-12-2021	По текущее время	12-12-2021	Среднее
  4	12-12-2021	По текущее время	12-12-2021	Низкое

  
  

  Таблица 3. Матрица рангов нечетких термов состояния объекта

  	Очень высокое	Высокое	Среднее	Низкое
  Очень высокое	1	0,7	0,4	0
  Высокое	–	1	0,8	0,3
  Среднее	–	–	1	0,6
  Низкое	–	–	–	1

  
  

• •    Сущность классифицируется как темпоральная или нетемпоральная.

• •    Темпоральная сущность может содержать нечеткий атрибут.

• •    Нечеткое значение атрибута зависит от темпорального значения атрибута.

• •    Темпоральный тип сущности должен иметь комбинированный первичный ключ, состоящий из атрибутов, изменяющихся и не изменяющихся во времени. Время начала активации является частью ключа.

Например, нечеткое темпоральное отношение (таблица 2) описывает данные о состоянии объектов, которое является нечетким атрибутом и которое может принимать разное значение (например, очень высокое, высокое, среднее, низкое). Состояние объекта меняется с течением времени, поэтому нечеткое значение, связанное с этим атрибутом, может изменяться при изменении времени. Рассчитанная матрица рангов нечетких термов состояния объекта показана в таблице 3.

Практическое применение отражено в виде запросов к базе данных с темпоральной поддержкой, к примеру, «выборка объектов с состоянием «Высокое» с 10 октября по 15 декабря».

Модель FuzzyEER

Модель FuzzyEER [3] представляет собой дополнение усовершенствованной модели сущность-связь (Enhanced Entity-Relationship model, EER) для создания концептуальных схем с помощью нечеткой семантики. Это расширение является эклектическим синтезом между различными моделями и предоставляет такие определения, как нечеткие атрибуты, нечеткие сущности, нечеткие отношения, нечеткие специализации и т. д. В данной модели определены нечетные значения, нечеткие атрибуты и нечеткие степени. Для каждого нечеткого типа атрибута определены два аспекта:

Таблица 4. Значения атрибута FuzzyType

Тип значения	Атрибуты
Неизвестен	null	null	null	null
Не определен	null	null	null	null
null	null	null	null	null
Точный	d	null	null	null
Метка	Fuzzy ID	null	null	null
Интервал	n	null	null	m
Приблизительное значение	d	d – m	d + m	m
Трапециевидный	α	β	γ	δ
Приблизительное значение d + m	d	d – m	d + m	m
Распределение возможностей с двумя значениями	p 1	d 1	p 2	d 2
Распределение возможностей с четырьмя значениями	d 1	d 2	d 3	d 4

• 1.    Способ представления значений (какие атрибуты хранить).

• 2.    Какая информация должна храниться в базе нечетких метазнаний для ее обработки и как эта информация должна быть организована.

Нечеткие атрибуты, которые позволяют хранить неточную информацию в упорядоченных базовых доменах:

• 1.    FuzzyType: атрибут хранит тип значения, соответствующий данным, которые планируется хранить. Определены 10 типов (таблица 4).

• 2.    FuzzyType 1–4 – имена этих атрибутов формируются путем добавления чисел 1, 2, 3 и 4 к имени атрибута. Они хранят описание параметров, определяющих данные и зависящих от типа значения (атрибута FuzzyType).

Для каждого возможного типа значения атрибута FuzzyType определены значения (таблица 4).

Таблица 5. Пример хранения FVP

ID	Имя	FVP
1	Наименование 1	[15.05.2021, 17.05.2021, 18.05.2017, 21.05.2021]
2	Наименование 2	[02.04.2021, 09.04.2021, 13.04.2017, 20.04.2021]
3	Наименование 3	[22.05.2021, 28.05.2021, 02.06.2017, 09.06.2021]

Таблица 6. Типы данных плохо-известной временной точки

ID	Значение	Представление
1	Момент времени	1 / x, x е t
2	Распределение возможностей в целочисленном домене	Нечеткое число или нечеткий интервал
3	Неизвестное значение	UNKNOWN = { 1 / t , V t е T }
4	Неопределенное значение	UNDEFINED = { 1 / 1 , V t е T }
5	Значение null	NULL = { 1 / Unknown, 1 / Undefined }

Таблица 7. Пример хранения PVP

ID	Имя	PVP (гранулярность – дни)
1	Наименование 1	[15.05.2021, 3, 2]	[18.05.2021, 1, 1]
2	Наименование 2	[11.02.2021, 8, 4]	[22.04.2021, 10, 13]
3	Наименование 3	[05.06.2021, 1, 5]	[08.06.2021, 2, 4]

В работах Jose Enrique Pons и других соавторов [4–6] представлена модель представления и обработки плохо-известных ( ill-known ) временных интервалов. Предложены два подхода: первый основан на нечетком периоде действительности ; второй – на возможностном периоде действительности .

Нечеткий период действительности ( Fuzzy Validity Period, FVP ) является нечетким интервалом, определяющим период действительности данного объекта.

В таблице 5 представлен пример хранения FVP. Период представляет собой атрибут трапециевидного типа с соответствующими вершинами а , р , у и 8 .

Главной особенностью FVP является оптимизация хранения. Компактное представление является результатом сопряженной семантики. Объект действителен на протяжении всего периода от начальной до конечной точки.

Возможностный период действительности ( Possibilistic valid-time period, PVP ) – это интервал, состоящий из двух плохо-известных (ill-known) точек и определяющий период действительности данного объекта. Важно отметить, что PVP представляет собой один четкий интервал, который (частично) не определен.

Плохо-известная временная точка (ill-known time point) – это неизвестный или частично известный некоторый момент времени. Точка может принимать только одно возможностное значение, но это значение не определено. Неопределенность относительно значения плохоизвестного момента времени X определяется как распределение возможностей в соответствии с выражением (1).

П- ( X ) = пХ ( t ) -е [ 0,1 ] , t е T. (1)

Типы данных для плохо-известной временной точки определены в таблице 6.

Плохо-известный интервал – это точный временной интервал, границы которого точно не определены. Во временном домене T двумя плохо-известными временными точками являются X , Y . Плохо-известный интервал определяется как [ X, Y ] . PVP является наиболее удобным представлением времени действительности. Для хранения PVP используются две точки распределения возможностей, одна для начала, другая для завершения действия объекта. В реализации применяется только треугольная функция принадлежности.

В таблице 5 представлен пример хранения PVP. Период представляет собой совокупность двух атрибутов [ S , E ] при S = [ D s , a s , b s ] , E = = [ D e , a e , b e ] , где D - точная дата начала или окончания действия, a и b – значения погрешностей .

д

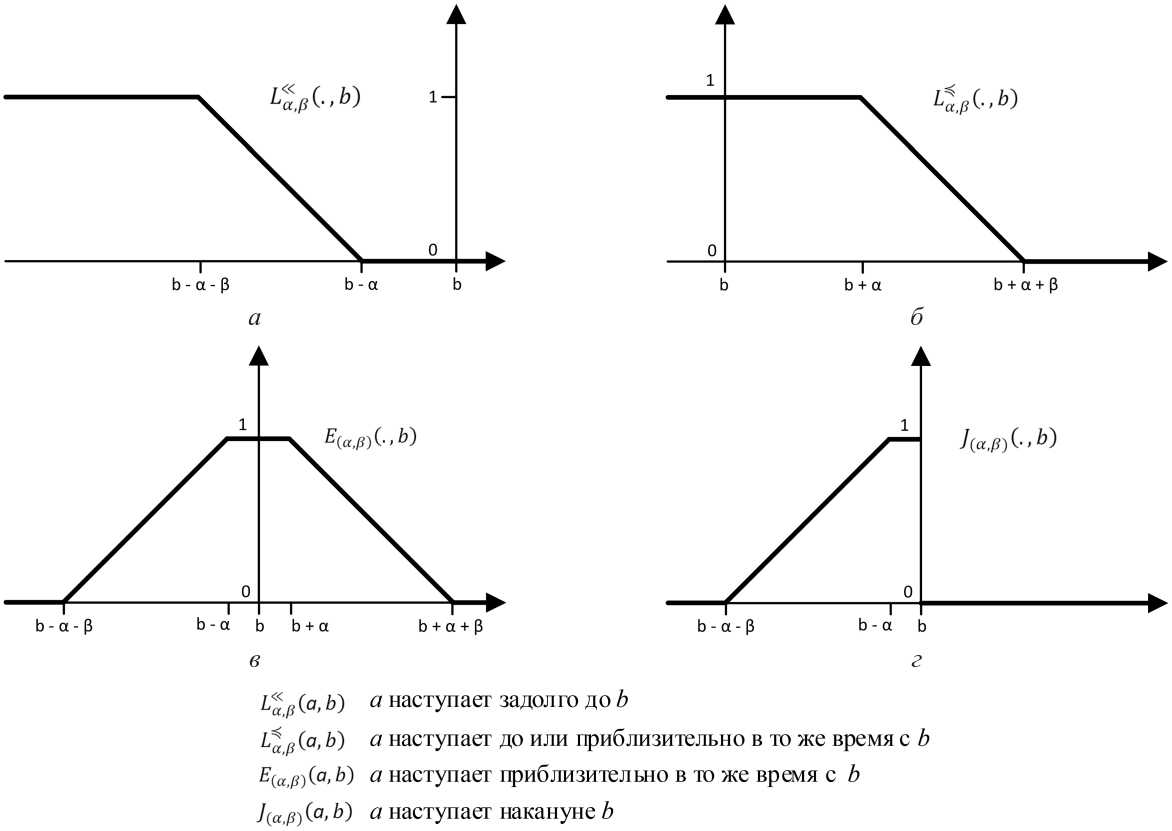
Рисунок 1. Нечеткое множество точек: а – задолго до b ; б – приблизительно в то же время с b ; в – приблизительно в то же время с b ; г – накануне b ; д – нечеткие отношения точек a и b

Нечеткие отношения временных интервалов, приведенные в работе Стивена Шокарта по фаз-зификации интервалов Аллена [7], основаны на порядках между временными точками интервалов. Целое число интерпретируется, к примеру, как число миллисекунд с 1-го января 1970 года или число лет с 1900 года. Примерами таких отношений являются a задолго до b, a накануне b, a и b приблизительно в одно и то же время.

Пусть ае R и в^Е [ 0, + х ] , то степень, в которой а задолго до b (в отношении ( а , в )) может быть выражена с использованием нечеткого отношения L 0 , в в R для всех а и b в R в соответствии с выражением (2).

1,

L:,(а. b )=К

b - а-а b - а > а + в b - а < а иначе

Параметры а ив определяют, как следует интерпретировать понятие «задолго до». Для временной точки, которая должна быть задолго до b со степенью 1, временной промежуток до b дол- жен быть как минимум а + в. Если промежуток времени до b меньше чем a, то временная точка задолго до b со степенью 0. Между точками при-сутсвует постепенный переход. На рисунке 1 изображены построенные нечеткие отношения.

Предположим, что временная точка соответствует количеству лет, начиная с января 1900 года. Используя значения а = 2 и в = 8, получим:

L ^ ( 20,23 ) = 0,125; L * 8 ( 20,23 ) = 1;

E2,8 (20,23) = 0,875; J2,8 (20,23) = 0,875, выражая, что 20 происходит задолго до 23 с низкой степенью, 20, но накануне 23 с высокой степенью и т. д. С другой стороны:

L 28 ( 23,20 ) = 0; L ^8 ( 23,20 ) = 0,875;

E 2,8 ( 23,20 ) = 0,875; J 2,8 ( 23,20 ) = 0.

Другими словами, 23 не происходит задолго или накануне 20, но происходит до или приблизительно в то же время, что и 20 с высокой степенью.

Неопределенный интервал времени (uncertain time interval, UTI) [8] представляет собой пару ( п ₅ , п e ), где п ₅ и п e - два распределения воз-

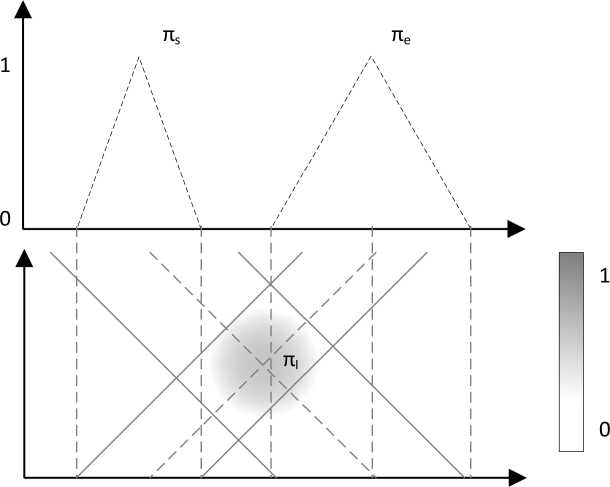
Рисунок 2. Построение UIZ в соответствии с UTI πI

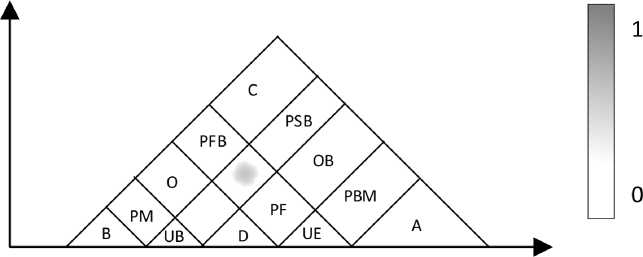
Рисунок 3. Неопределенные зоны отношений URZ

можностей выпуклой формы, отражающих знания о начальной и конечной точках интервала UTI. В случае определенности распределение возможностей характеризуется одноэлементным нечетким множеством с единственной точкой пространства решений, содержащей четкую дату. В случае неопределенности распределение возможностей характеризуется нормализован- ным нечетким множеством, содержащим все возможные значения дат и связанные с ними степени возможности. В совокупности оба распределения возможностей отражают имеющиеся знания о начале и конце интервала UTI, которые они моделируют. Это означает, что пs и пe вместе представляют собой еще одно распределение возможностей п1, состоящее из всех возможных временных интервалов, которые могут быть построены из пs и пe. Для каждого интервала времени [ts, te ] его связанная степень возможности в п1 вычисляется формулой (3).

^п 1

( [V . ] ) -

, min(п, (t, ).пe (te )), 0, иначе t

^. (3)

Для каждого UTI п1, характеризующегося двумя распределениями возможностей пs и пe, может быть построена соответствующая неопределенная зона интервала (uncertain interval zone, UIZ), как показано на рисунке 2.

Распределение возможностей пs определяет интервал |t", t, |. в котором находится начальная точка UTI, тогда как п_e определяет интервал [ te, te~\, в котором находится конечная точка UTI. Следовательно, все возможные интервалы времени для UTI содержатся в отрезке Гt,, te I (или в течение) и содержат интервал I t,, te I. С использованием т. н. зоны отношений (crist relation zones CRZ), соответствующим отношениям Аллена «в течение» и «содержит», получается, что UTI должен быть расположен в четырехугольной зоне из двух прямых, которые соответственно проходят через t, и t, под углом а, и две прямые линии, которые соответственно проходят через te и te под углом а. Построены пятнадцать зон отношений URZ (неопределенные зоны отношений CRZ), которые изображены на рисунке 3. Множество отношений обозначается как:

RU = {B, O, C, D, OB, A, PM, PS, PFB, PE, PSB, PF, PMB, UB, UE},

Рисунок 4. Пример использования подхода нечеткой визуализации

где каждое значение определяет классическое отношение Аллена (два дополнительных UB – «неточно перед» и UE – «неточно равен»).

Эти зоны предназначены для получения информации о неточности отношений интервалов UTI.

Пусть дано упорядоченное множество моментов времени T, точный интервал времени I = [1, 3] и интервал времени J, чей начальный момент времени определяется треугольным распределением возможности на T с центром {5} и поддержкой [2,7] конечным моментом времени, который определяется треугольным распределениемвозможности на T с центром {12} и поддержкой [9,15]. Визуализация примера изображена на рисунке 4. Интервальная точка для I лежит в зоне URZ «PM». Степень возможности находится выше нуля для отношений «встречает», «перед», «перекрывает» между отношениями I и J. Так как зона в отношении «пересекает» очень светлая, зона в отношении «встречает» также светлая и зона в отношении «перед» очень темная, можно предположить, что I пересекает J с низкой степенью возможности, I встречает J с такой же низкой степенью возможности, но степень возможности I перед J равна 1.

Возможностно-темпоральная модель данных PTDM (Possibility Temporal Data Model) (рисунок 5) позволяет формализовать способы представления и хранения данных путем определения нечетких типов, атрибутов и их значений в базе нечетких метазнаний, а также формализовать способы взаимодействия нечетко-темпораль- ных данных на основе алгебры возможностно-темпоральных отношений между точками и/или интервалами.

В модели PTDM были расширены определения временной точки и интервала [9].

Возможностная временная точка pt – предполагаемая временная отметка или момент времени на временной оси, значение которой неизвестно либо определено неточно.

Возможностный интервал {pts, pty} - промежуток времени между двумя возможностными временными точками.

Введены следующие типы возможностных временных точек:

• 1.    Точное значение точки.

• 2.    Определяет точное значение временной точки для возможностного типа.

• 3.    Значение определено с возможным отклонением. Предполагаемое значение временной точки принимает степень возможности PExtent, значения возможностного отклонения от времени наступления находятся в диапазоне [0, PExtent]. Вид: pt - a, pt, pt + Р, PExtent, где pt е T -возможностная временная точка, предполагаемый момент времени на временном отрезке T; а и р - значения возможностного отклонения от наступлени).

• 4.    Значение в диапазоне не определено. Значения в диапазоне имеют одинаковую степень возможности наступления = PExtent.

• 5.    Значение не определено. Любые значения имеют одинаковую степень возможности наступления = 0.

Вид: |^{pts, pty}, PExtentJ, где {pts, pty }е T -диапазон значений возможностных временных точек предполагаемого момента времени на вре-

Рисунок 5. Возможностно-темпоральная модель PTDM

менном отрезке T. pt_s и pt_y могут принимать пустое значение. В таком случае предполагается диапазон значений в виде: [{pt_s, х},PExtentJv |{х, pty }, PExtent J.

Вид: [undefined, 0].

Алгебра отношений

На основании темпоральных отношений точек и/или интервалов, а также введенных типов возможностных временных точек разработана алгебра возможностно-темпоральных отношений точек и/или интервалов модели PTDM.

Отношения основываются на сравнении точек (в случае интервалов – точек начала или окончания действия). Основными отношениями между точками являются отношения «Перед», «После» и «Равен». Рассмотрим расширенную версию отношения «Перед»: «Накануне» (PosJustBefore PJB) – точное значение точки a и возможностная точка b с периодами возможного отклонения наступления а и р в соответствии с выражением (4).

0,  (а - a > b - а) v (b< a);

(b - а) - (а - a)

PJB = <

b-а

(а - a< b - а) л (a< а);

• 1,  a = а;

  
  

  b-a Ib-а^,

  
  

  а < a< b.

  
  

Библиотека алгоритмов PTL (Possibility Temporal Library) включает в себя PL/SQL пакет функций и процедур возможностно-темпораль-ной алгебры для реляционных баз данных, а также SOAP веб-сервис для выполнения отношений возможностно-темпоральной алгебры.

Функции PL/SQL пакета представляют собой алгебру возможностных отношений точек и интервалов и предназначены для сравнения как точных, так и возможностных дат и периодов. Например, функция PosJustBefore «накануне» возвращает логический результат сравнения или степень, с которой одна точка/интервал находится «накануне» другой точки/интервала.

Приведем пример вызова функции PosJustBefore:

DECLARE

• a possibledate;

• b possibledate;

0.27                                  /              \

extent_result NUMBER(3,2);

BEGIN a := possibledate (‘1’, TO_DATE (‘202107-25   09:12:00’, ‘yyyy-mm-dd hh24:mi:ss’),

NULL,NULL,NULL);

b := possibledate (‘3’, NULL, NULL, range_fuz_ def (TO_DATE (‘2021-07-25 10:00:00’, ‘yyyy-mm-dd hh24:mi:ss’), TO_DATE(‘2021-07-25 11:00:00’, ‘yyyy-mm-dd hh24:mi:ss’), 0.8), NULL);

dbms_output.put_line (‘PosJustBefore extent = ‘ || FUZ_UTIL.POSJUSTBEFORE (a,b));

dbms_output.put_line (‘PosJustBefore result = ‘ ||

⁰                  а* а Б        Р ^

Результат функции PosJustBefore

PosJustBefore (a, b) = 0.27

PosJustBefore (a, b, 0.4) = false

Рисунок 6. Визуализация результата выполнения функции PosJustBefore

CASE FUZ_UTIL.POSJUSTBEFORE (a, b, 0.4, extent_result);

WHEN true THEN ‘True’

ELSE ‘False’

END || ‘ where resulted extent = ‘ || extent_result);

END;

/

Визуально результат вызова функции может выглядеть, как изображено на рисунке 6.

Веб-сервис библиотеки PTL представляет собой интерфейс, вызываемый другими системами для выполнения отношений возможностно-темпоральной алгебры. Приложение клиентской стороны подключается к SOAP веб-сервису с использованием определенной XML структуры (wsdl) и вызывает необходимые методы.

Пример возвращаемого ответа на вызов метода «Накануне» для двух возможностно-темпо-ральных точек представлен ниже. Сформирован SOAP запрос, включающий в себя две сравниваемые временные точки с TYPEID = 1 и 2. Запрос направляется на сервер, который в свою очередь выполняет операцию сравнения в соответствии с реализованной алгеброй. Степень возможности как результат сравнения возвращается в SOAP ответе в соответствии со структурой xml.

/soap/envelope/”xmlns:xsd=”http://www. ” xmlns:xsi=”http://www. ”>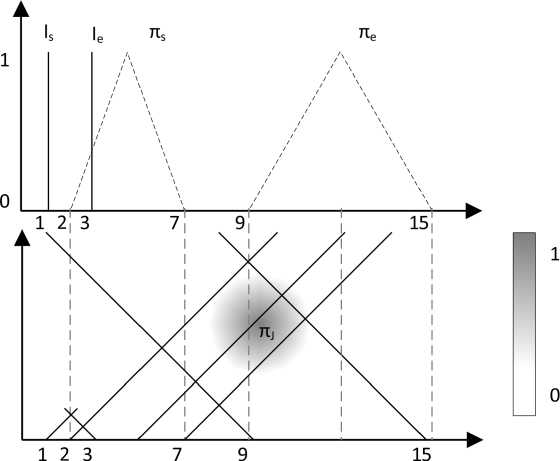

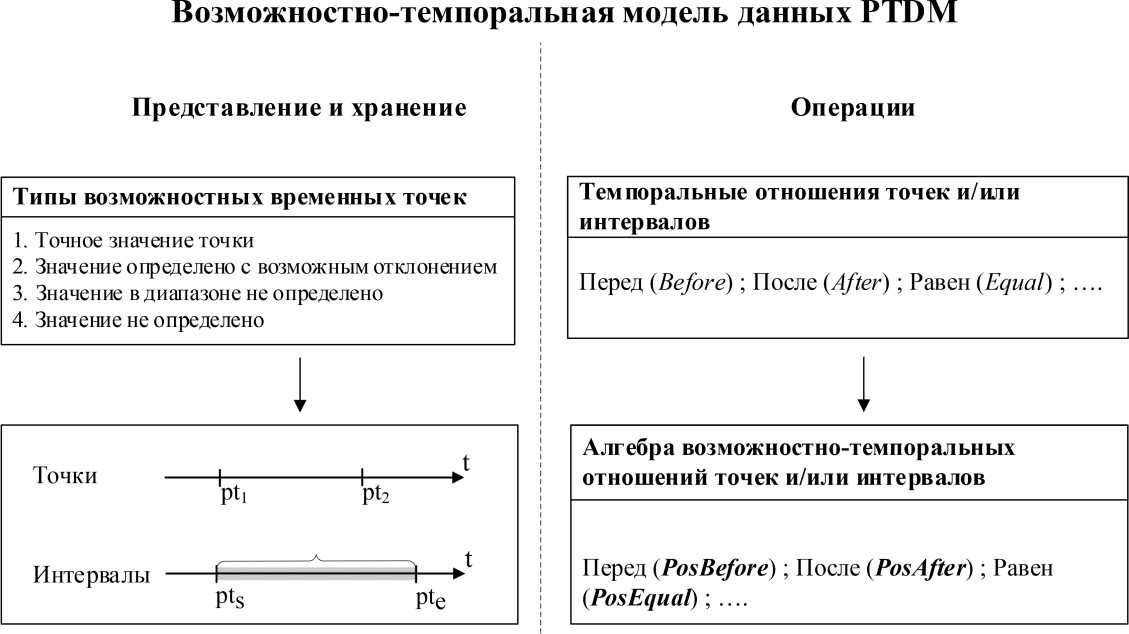
0.47 posJustBeforeReturn>

Таблица 8. Отношения, используемые в процессе формирования отчета

#	Описание
Перед	PosBefore (a {POSSIBLEDATE с подтипом RANGE_FUZ_DEF}, b {POSSIBLEDATE с подтипом DATE_FUZ})
После	PosAfter (a {POSSIBLEDATE с подтипом RANGE_FUZ_DEF}, b {POSSIBLEDATE с подтипом DATE_FUZ})
Равен	PosEqual (a {POSSIBLEDATE с подтипом DATE_FUZ}, b {POSSIBLEDATE с подтипом DATE_FUZ})

Рассмотрим пример интеграции библиотеки PTL с аналитической системой предприятия. Система аналитики использует механизмы фиксации предполагаемых дат платежей на основании показателей прошлых периодов и позволяет визуализировать результаты в статистическом виде по запрашиваемым периодам. В логике формирования фигурируют две возможностные точки – дата предполагаемого платежа и сравниваемая возмож-ностная дата выбираемого периода. Платежи фиксируются в базе данных с типом данных атрибута «Дата платежа» как «возможностная дата». Пользователь выбирает необходимые критерии, после чего система аналитики инициирует процесс формирования отчета по заданным условиям. Используемые отношения представлены в таблице 8.

Система анализирует выбранные пользователем критерии и выполняет выборку показателей в соответствии с запросом.

В модели FuzzyEER (используемой в дальнейшем в моделях FVP и PVP) определены 11 типов данных нечетких темпоральных атрибутов объ-

Таблица 9. Точная точка со степенью возможности

Дата начала Дата завершения 2021-01-10 10:00:00 [00:00:00, 2021-01-15 09:30:00, 00:00:00, 0.65] екта. При этом важно отметить, что в моделях для темпоральных данных применяются только два из них: трапециевидный и треугольный. Это означает, что внешняя система или пользователь ограничены только двумя типами хранения дат, для которых применимы нечеткие отношения.

В PTDM модели определены 4 основных типа, предоставляющих возможность создавать различные комбинации точек или интервалов:

• 1.    Можно определить интервал, в котором одна точка является точной, а другая возмож-ностной. Можно определить две точные или две возможностные даты.

• 2.    Возможностную точку можно определить одной из 4х типов.

• 3.    Точный интервал или точку можно определить со степенью возможности, к примеру (таблица 9):

Интервал начинается с точной даты, а заканчивается со степенью возможности (рисунок 7).

Такой подход предоставляет бо́льшую гибкость в формировании возможностно-темпораль-ных точек или интервалов.

Классическая темпоральная алгебра Аллена определяет отношения между интервалами.

PTDM основывается на отношении точек, т. е. двух точек между собой или точек интервалов. В библиотеке PTL темпоральная алгебра Аллена расширена посредством разбиения отношений интервалов до отношений между точками, а также точками и интервалами (таблица 10).

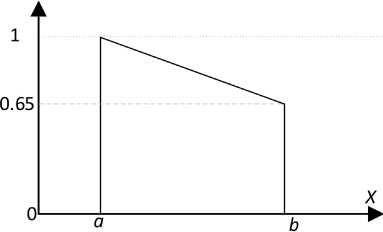
Рисунок 7. Визуализация интервала с точной точкой начала и возможностной точкой завершения действия

UTI основана на интервалах, поэтому нечеткие отношения определяются только для интервалов. UTI не позволяет производить сравнение возможностных точек. При этом отношения не учитывают грани интервалов (начало, середина, конец), к примеру, интервалы могут пересекаться гранями, но отношение «Перед» всегда вернет степень «1», т. е. один интервал точно находится перед вторым.

Возможностно-темпоральная модель PTDM, в свою очередь, позволяет производить отношение между:

• 1)    возможностно-темпоральными точками;

• 2)    возможностно-темпоральными интервалами;

• 3)    возможностно-темпоральными точками и интервалами;

• 4)    точными точками/интервалами и возмож-ностно-темпоральными точками/интервалами.

Также в обязательном порядке учитываются грани точек и интервалов. В случае пересечения точек библиотека алгоритмов производит расчет в соответствии с запрашиваемым отношением.

Нечеткие отношения Стивена Шокарта не учитывают классические отношения Аллена,

Таблица 10. Введенные отношения временных точек и интервалов

Наименование отношения	Точки A, B и интервал J		Визуализация
Перед (Before)	A перед J A перед B	A < S At < Bt	A J     В ------------------►t
После (After)	A после J A после B	A > E At > B:	В J     A ------------------kt
Равен (Equal)	A равен B	At = Bt	A. ________15______>t
Содержит (Contains)	J содержит A	S < At < '	A. J ------------------kt
Начинает (Starts)	A начинает J	S=At < E	A.__________J_ ------------------kt
Завершает (Finishes)	A завершает J	S < At = 1	J_______A. ------------------kt

Таблица 11. Темпоральная структура данных с нечеткими состояниями объекта

ID	Дата начала	Дата завершения	Состояние
1	10-01-2021 10:15	11-01-2021 06:00	Низкое
2	11-01-2021 06:00	11-01-2021 06:01	Высокое
3	11-01-2021 06:01	13-01-2021 15:00	Среднее
4	13-01-2021 15:00	По текущее время	Нормальное

Таблица 12. Возможностно-темпоральная структура данных с нечеткими состояниями объекта

ID	Дата начала	Дата завершения	Состояние
1	[10-01-2021 10:15, 1.0]	[10-01-2021 22:00, 1.0]	Низкое
2	[10-01-2021 22:00, 1.0]	[08:00:00, 11-01-2021 06:01:00, 00:00:00, 1.0]	Высокое
3	[11-01-2021 06:01, 1.0]	[13-01-2021 15:00, 1.0]	Среднее
4	[13-01-2021 15:00, 1.0]	По текущее время	Нормальное

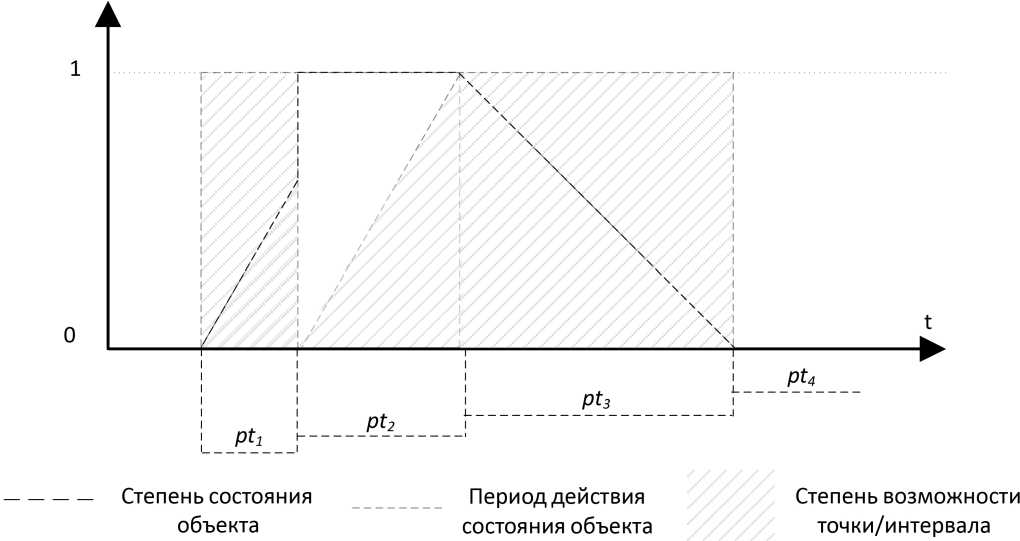
Рисунок 8. Визуализация периода действия состояний объекта

а используют нечеткие семантические дополнения этих отношений. При этом отношения сравнивают только точные точки и интервалы. Нечетким является только результат их сравнения. Данная модель не предоставляет возможность сравнивать неточные точки и интервалы, а также не существует возможности использовать нечеткую интерпретацию отношений Аллена.

PTDM предоставляет возможность сравнивать как точные, так и неточные точки, интервалы. Помимо этого, библиотека включает в себя дополнительные отношения (накануне / задолго до / начало / середина / конец).

Подход нечеткости и темпоральности

Модель FTRM описывает подход темпоральной нечеткости, т. е. подразумевается, что нечеткими данными в этой модели являются только состояния объектов, а не время их действительности. В данной модели применяется классиче- ская темпоральная структура с точными датами начала и завершения действия состояния объекта.

Возможностно-темпоральная модель PTDM, в свою очередь, включает в себя два подхода: нечеткой темпоральности и темпоральной нечеткости, то есть помимо нечетких состояний объекта можно фиксировать нечеткий период их действия. Например, с использованием классической темпоральной структуры можно зафиксировать нечеткие состояния объекта в следующем виде (таблица 11).

В данном примере состояния объекта являются нечеткими атрибутами. С использованием воз-можностно-темпоральной модели PTDM можно более подробно зафиксировать период действия состояний (таблица 12).

Визуально период действия состояний можно изобразить следующим образом (рисунок 8):

Поддержка двух описанных подходов позволяет возможностно-темпоральной модели PTDM

Таблица 13. Таблица платежей за один расчетный период

ID	Тип услуги	ID услуги	ID периода	Дата платежа	Сумма платежа
13758920	Mobile	030739898	40617053	24-01-2021 19:07:15	1275.12
13918711	Mobile	0013123648	40617073	29-01-2021 19:03:00	17.93
12089807	Mobile	02079783315	40617113	01-01-2021 16:13:21	869.92
11687154	Mobile	1005440023	40617133	09-01-2021 14:50:26	0.09

предоставлять расширенный набор инструментов для работы с нечеткими и нечетко-темпоральными данными.

Интеграция

Библиотека алгоритмов PTL модели PTDM построена, во-первых, как пакет для баз данных, который может использоваться непосредственно в БД при написании процедур, функций или триггеров для хранения или сравнения точек/ интервалов; или же может вызываться по интерфейсам ODBC/JDBC внешними приложениями. Во-вторых, как веб-сервис, выполняющий роль стандартизированного общепринятого SOAP-интерфейса для внешних систем (даже из других сетей), предназначенный для выполнения расчетов методов сравнения возможностных точек/ интервалов. И в-третьих, как аналитический инструмент отчетности, визуализирующий результаты возможностно-темпоральных отношений в человеческом виде посредством взаимодейстия с базой данных для выполнения функций отношений.

Модели FVP и PVP, в свою очередь, построены только с использованием Hibernate фреймворка, т. е. пользователи, использующие данные модели, обязательно должны знать язык программирования Java; системы должны «уметь» интегрироваться с соответствующим интерфейсом. При этом не предоставляются готовых инструментов визуализации данных.

Набор инструментария библиотеки алгоритмов PTL предоставляет возможность для развертывания и интеграции библиотеки в любой БД и для использования системами, написанными на любых языках.

Показатели производительности

Оценка показателей производительности выполнения операций библиотеки алгоритмов PTL модели PTDM проводилась в СУБД Oracle с разными объемами данных [10]. Показателем производительности являлось время выполнения классических SQL операторов сравнения Oracle и отношений возможностно-темпоральной модели. Анализ проводился для всех возможностно-темпоральных отношений. Использованное аппаратное и программное обеспечение: Intel Core i7-3520M CPU 2.9 GHz, 8 GB RAM, SSD 250GB, OS Linux version 2.6.18-404.el5 CentOS release 5.11, Oracle Database 12.1.0.2.0.

Была использована таблица c платежами за один расчетный период. Пример содержимого таблицы (таблица 13).

Таблица наполнялась данными инкрементально после каждого шага тестирования. Время отработки запросов рассчитывалось как среднее значение нескольких выполняемых запросов подряд. Тестирование разделялось на два этапа:

• 1.    Сравнение показателей выполнения отношений между точными точками с использованием классического оператора сравнения SQL и с использованием возможностно-темпорального отношения.

• 2.    Сравнение показателей выполнения воз-можностно-темпоральных отношений двух типов: «значение определено с возможным отклонением» и «значение в диапазоне не определено».

Результаты тестирования показали, что производительность отношений двух точных точек с использованием возможностно-темпорального отношения отличается от результатов классического оператора SQL приблизительно на 5–6 %. Это то значение времени, которое отношение использует для расчета результирующей степени возможности, а также для его сравнения со значением, поступившим для удовлетворения условия. При этом важно учитывать, что с увеличением объема данных рост значения процента не наблюдается. Сравнение отношений между возможностными точками проводилось для двух типов возможностно-темпоральной модели. Результаты показали примерно одинаковые значения производительности независимо от объема тестируемых данных. Пример результатов тестирования точного SQL оператора сравнения и отношения возможностно-темпоральной модели изображены в таблице 14.

Важно отметить, что результаты показателей отношений между возможностными точками не сравнивались с показателями точных точек ввиду различных областей применения данных подходов, поскольку классические операторы для работы с точными данными не позволяют рассчитывать результирующие возможностные степени,

Таблица 14. Результат тестирования производительности

	10000	20000	30000	40000	50000	60000	70000	80000	90000	10000
a < b	98 мс	205 мс	305 мс	402 мс	525 мс	630 мс	781 мс	871 мс	981 мс	1154 мс
PosBefore (a,b)	105 мс	220 мс	330 мс	428 мс	570 мс	666 мс	845 мс	920 мс	1020 мс	1199 мс

которые являются обязательными для нечеткой модели.

Представленный в данной статье сравнительный анализ моделей обработки нечетких темпоральных данных демонстрирует наличие отличительных характеристик возможностно-темпоральной модели данных PTDM и библиотеки алгоритмов PTL в ряде факторов. Рассмотренные модели имеют существенные ограничения и специфические сложности, которые были учтены при разработке модели PTDM. Часть таких ограничений приведена ниже.

• 1.    Существующие коммерческие СУБД позволяют оперировать только точными темпоральными данными без возможности определения нечетко-темпоральной структуры, а также без поддержки алгоритмов обработки нечетко-темпоральных данных.

• 2.    Систематизируются нечеткие интервалы без поддержки и алгоритмизации обработки нечетких точек с ограниченно выделенными нечетко-темпоральными отношениями между возмож-ностными точками и/или интервалами.

• 3.    Ограниченно учитывается погрешность в нечетких диапазонах интервалов без анализа гранулярности в диапазонах нечеткости событий или интервалов.

Эффективность возможностно-темпоральной модели данных PTDM отражается в наличии расширенных функциональных характеристик данной модели, в частности, при определении типов данных для точек и/или интервалов, при выполнении отношений между точками и/или интервалами, при использовании расширенного набора возможностно-темпоральных отношений, при интеграции модели с другими системами или сервисами, а также при анализе полученных показателей производительности. Полученные результаты демонстрируют готовность модели применяться в прикладных областях и технологиях обработки данных.

Исследование выполнено при финансовой поддержке РНФ в рамках научного проекта

№ 22-49-02023 «Разработка и исследование методов повышения надежности привязных высотных беспилотных телекоммуникационных платформ нового поколения».