Возможные направления развития экономики при кризисе и росте в взаимосвязи с населением страны

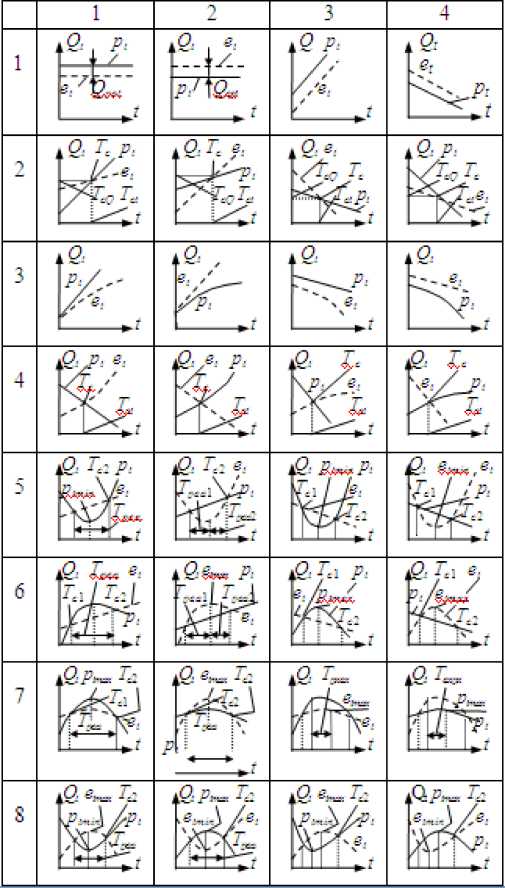
На рост или спад экономики влияет большое количество факторов, одним из которых является рост или уменьшение, по объективным причинам, населения. Для того чтобы выявить взаимосвязь между теоретическим ростом или спадом экономики e t , и соответственно, теоретическим ростом или уменьшением численности населения p t была разработана таблица, в которой представлены возможные варианты взаимосвязи рассматриваемых переменных e t и p t . В данном случае под словом экономика будем понимать ВВП или ВВП на душу населения в рассматриваемой стране. Поэтому в зависимости от контекста будет использоваться либо любое ВВП, либо слово экономика. На графиках в таблице была изображена одна ось абсцисс Q t вместо двух Q et и Q pt с разными масштабами и значениями, где Q_et и Q_pt представляются в процентном отношении. То есть, если взять любую точку на временной оси ординат t , например, 24 марта 1950 года или 11 сентября 1990 года, то принимается, что в ней ВВП - Q_et = 100% и численность населения Q_pt = 100%. Эти точки и будет началом отсчета и в дальнейшем строятся изменения Q_et = f(t ) и Q_pt = f(t ) относительно данных точек с требуемым шагом. Здесь и далее во всех графиках в таблице пунктирной линией изображен параметр e t , а сплошной линией параметр p_t. Ряд возможных вариантов развития переменных e t и p t представлены ниже в таблице.

В первом варианте экономика e_t и население p t являются величинами постоянными и не изменяются во времени, т.е. e_t = const и p_t = const (см. 1 строку). Здесь и далее первая цифра указывает номер строки, а вторая - столбца. Изменения p_t и e_t описываются линейным уравнением вида y et = Q et и У р, = Q pt .

В ячейке 11 представлен вариант, когда количество населения Q pt преобладает над экономическими показателями Q_et , т.е. Q_pt > Q_et . Чтобы охарактеризовать такое состояние экономики и населения введем переменную Q pet , которая характеризует теоретическую разницу между переменными Q pt и Q et и рассчитывается по следующей формуле (1)

Q pet = Q pt ~ Q et .

В этом случае, чем больше величина Q pet , тем ниже жизненный уровень населения, т.к. потребление на душу населения уменьшается. Для простоты рассуждений, будем считать, что как элита с олигархами, так средний класс и малообеспеченные потребляют одинаковое количество товаров, продуктов и сервисных услуг. Если же этого не учесть, то с увеличением величины Q pet класс элиты и олигархов, как минимум, не захочет ухудшать своё благосостояние, поэтому, жизненный уровень среднего класса и малообеспеченных будет уменьшаться.

Следовательно, здесь могут возникнуть следующие различные варианты или их комбинации развития ситуации, ряд из которых представлен ниже:

• 1.    население будет безропотно сносить ухудшение своего положения;

• 2.    население, при любой возможности, будет легально и нелегально иммигрировать в более развитые экономические страны и, в первую очередь, в те страны, где рождаемость населения падает и где не хватает рабочих рук, что и наблюдается в настоящее время;

• 3.    правительство страны, чтобы отвлечь население от демократических преобразований, начнет войну с соседним более слабым государством, что и было сделано Ираком в 1990-1991 гг.;

• 4.    население путем демократических выборов сместит существующее правительство, и возможно правящий класс, как это было сделано в Чили, Венесуэле и т.д.;

• 5.    население подымится на революцию и сместит существующий строй, как это произошло недавно в Румынии.

В ячейке 12 показаны зависимости, когда экономические показатели преобладают над населением, т.е. Q et >  Q pt . При этом варианте уровень жизни населения будет тем выше, чем больше величина Q ept , рассчитываемая по формуле (2), что, естественно, приводит к увеличению благосостояния всего населения.

Q ept = Q et ~ Q pt . (2)

Зависимости e_t и p_t изменяющиеся по линейному закону можно охарактеризовать углом наклона а конкретной прямой к оси ординат. В рассматриваемом варианте во всех случаях ос = 0°. Теоретически же угол наклона oc t может лежать в следующих пределах -90° < oc t < +90°. Таким образом, знак угла ос показывает рост (если +) или спад (если ) рассматриваемых переменных (ячейки 13 и 14).

Угол t , для всех рассматриваемых случаев, может иметь следующие пределы:

для страны с небольшим населением -90° = oc _pt < +90°, т.е. население небольшой островной страны и её экономика может моментально либо погибнуть, либо произойдет существенный спад, например, или при землетрясениях в Турции в 1994 г.[3] и в Гаити в 2010 г. и др. [1, 2];

для страны с большим количеством населения или для населения Земли -90° <  a_pt < +90°. Здесь даже при падении на Землю большого метеорита или астероида население Земли и экономика отдельных стран будет существовать, как минимум, какой-то период времени. Например, при цунами как это случилось в Индонезии в 2004 г. [4].

Таблица 1 - Варианты взаимосвязи изменения теоретической экономики еt и теоретической численности населения p_t

На основе формул 1 и 2 можно ввести следующие параметры, характеризующие экономику и население:

Q_etmin ~ минимальное теоретическое состояние экономики e t , ниже которого начнется либо вымирание населения из-за голода, холода и т.п., либо населе-

Возможные направления развития экономики при кризисе и росте в взаимосвязи с населением страны ние свыкнется со своим положением и будет влачить такую жизнь, либо население подымится на революцию и сместит существующее правительство и изменит строй. В этом случае население может терпеть невзгоды только при условии, что они связаны с защитой отечества от врага или при каких-либо катастрофах планетарного характера и т.п. (ВВП, руб., доллар, евро и т.п.), ед.;

Q_etmax ~ максимальное теоретическое состояние экономики e t , выше которого население физически не сможет воспользоваться производимыми товарами и услугами, при условии, конечно, что численность населения не растет и остается постоянным. Эта точка также становится начальной точкой стабилизации или спада роста экономики e t , либо излишки надо будет экспортировать (ВВП, руб., доллар, евро и т.п.), ед.;

Q_ptmin ~ минимальная теоретическая численность населения страны (Земли) p t , ниже которой произойдет вымирание нации ввиду невозможности естественного воспроизводства, чел.;

Q_ptmax ~ максимальная теоретическая численность страны (Земли) p t , выше которой население физически не сможет себя прокормить, производить соответствующее количество товаров, услуг и т.д. по тем или иным причинам. Эта точка также становится точкой начальной стабилизации или спада рождаемости населения. Такое состояние может привести к радикальным решениям, таким как военные действия, либо природа сама начнет регулировать количество населения за счет катаклизмов, болезней и т.д., чел.

В строке 2 показаны варианты изменения экономики e t и численности населения p t по линейному закону, когда построенные зависимости пересекаются в точке T c , которая имеет значения T ct и T_cQ на соответствующих осях координат t и Q t .

В рассматриваемом случае возможны следующие четыре варианта развития:

• •    население p_t растет более высокими темпами, чем экономика e t , ячейка 21. В этом случае целесообразно, чтобы значение T_ct было максимальным, что по-

• зволит отодвинуть обнищание населения страны;

• •    экономика e_t растет более высокими темпами, чем население p t , ячейка 22. В этом случае целесообразно, чтобы значение T_ct было минимальными. Это позволит повысить благосостояние населения за короткий промежуток времени;

• •    экономика e_t падает более быстрыми темпами, чем население p t , ячейка 23. В этом случае целесообразно, чтобы величина T_ct была максимальным. Это не допустит обнищание населения быстрыми темпами и позволит принять экстренные меры как по увеличению численности населения страны, так и поднятия экономики в целом;

• •    население p t уменьшается более высокими темпами, чем экономика e_t, ячейка 24. В этом случае целесообразно, чтобы величина T_ct была как можно меньше. Это позволит повысить благосостояние населения за минимальное время.

Далее в строках 3 и 4 показаны варианты развития переменных e t и p t , когда одна из них изменяется по линейному закону, а другая по более сложному, причем в 4 строке переменные также пересекаются в точке T_ct. Для этих двух строк приемлемы выводы, сделанные для строки 2.

В следующих двух строках показаны более сложные варианты развития переменных e_t и p_t, где одна из зависимостей имеет максимум или минимум и две точки пересечения с другой зависимостью, которая изменяется по линейному закону. Для этих вариантов были введены следующие параметры: T_pea - разница между координатами точек пересечения T_{pe 2} и T_pe 1 любой кривой p_t ( e_t ) с прямой или другой кривой e t (p t ), ед.; T peai - разница между координатами точек пересечения T pe 1 части кривой p t ( e t ) с прямой или кривой e t (p_t ) и минимальным (максимальным) значением T pmin , T pmax ( T emin , T e-max ) кривой p t ( e t ), ед.; T pea 2 - разница между координатами точек пересечения T_{pe 2} части кривой p t ( e t ) с прямой или кривой e t ( p t ) и минимальным (максимальным) значением T pmin , T pmax ( T emin , T emax ) кривой p t ( e t ), ед. и ряд других.

Здесь должны быть следующие значения рассматриваемых параметров:

Для параметров A e t и Рр( (см. ниже рис. 1 и описание к нему):

• •    ячейки 51,53:

до минимальной точки: - A p_f -> max ;

после    минимальной    точки:

ррt —> min ;

• •    ячейки 52, 54:

до      минимальной      точки:

• — A e_t —> min ;

после    минимальной    точки:

A e_t —> max .

Для параметров T_pea:

• •ячейка51:

T pea  ^ ^max , T pea l -^ max , ^T pea 2 ~> maX ;

• •    Ячейка ^{52: T} _pea -^ mln , T pea i -^ min , T pea 2 -> min ^;

• • ячейка53:

Tpea ^ max , ^T pea1 -^^max , T pea 2 “► max ;

• • ячейка54:

^Tpea “> min , T peal ^ min , T pea 2 ^ min .

В этом варианте при выборе максимальных или минимальных значений рассматриваемых параметров появилась двойственность их трактовки. Так, например, если в ячейке 54 параметр Tct 1 будет максимальным, то экономическое благосостояние населения будет долго снижаться, а потом быстро возрастет.

Если же значение параметра T_ct 1 будет минимальным, то экономическое благосостояние населения быстро упадет, но зато и быстро возрастет. В данном случае, по мнению автора, целесообразно конечно выбрать второй вариант развития, где T ept 1 —> min .

Для расчета новых параметров можно воспользоваться формулой (3) T pea = T pea 1 ⁺ T pea 2 = T ct 2 ^_ T ct 1 = ⁽ T ptmin ^—

T ct 1 ) + ( T ct 2 - T ptmin ),

где: Tca 1, Tptmin и др. координаты соответ- ствующих точек на оси t.

Описанные выше варианты с наклонной прямой приемлемы и для случая, когда одна из переменные et или pt представляет собой прямую параллельную оси t. Тогда эта прямая будет иметь следующие параметры: ccet = 0°,apt = 0°, ±Aet = 0 и ±Apt = 0. Где ±Aet - прирост или рецессия экономики в рассматриваемый промежуток времени Ate, ед. (рис. 1 a); ±Аpt - прирост или убыль населения в рассматриваемый промежуток времени tp, чел. (рис. 1b). То есть нам необходимо знать, на сколько увеличатся или уменьшатся переменные et и pt за промежуток времени Ate или Atp. В данном случае значения Ate и Atp следует принять равными между собой, т.е. Ate = Atp.

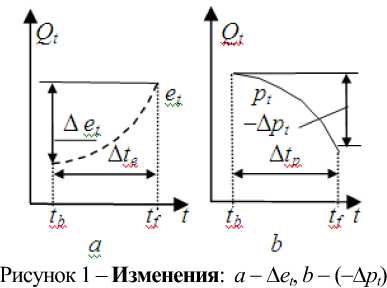
На практике значения A t e и A t_p целесообразно принять единице, т.е. одному часу, дню, неделе, месяцу или году, в зависимости от конкретных условий и возможности оперативно получить достоверную информацию об произошедших изменениях в экономике или с населением. Таким образом, для переменных e t и p t изменяющихся по сложному закону можно записать следующее шесть выражений:

• 1 . pp_t - |-A et | = 0;

• 2 . pp_t - |-A et | > 0;

• 3 . A p t - |-A e t | < 0.

• 4 . A e t - |-A p t | = 0;

• 5 . A e t - |-A p t | > 0;

• 6 . ee_t - |-A p t | < 0.

Вариант представленный в строке 6 аналогичный вышеописанному варианту только здесь кривая имеет максимум. При этом кривая сначала увеличивается до своего максимума T emax ( T pmax ), а потом уменьшается и дважды пересекает прямую. В ячейках 61 и 62 рассматриваемые прямые возрастают, а в ячейках 63 и 64 уменьшаются.

Здесь должны быть следующие значения рассматриваемых параметров:

Для параметров A e t и A p t :

• •    ячейки 61,63:

до      максимальной      точки:

pp_t —> min ;

после    максимальной

-Иф_t -» max .

• •    ячейки 62,64:

до     максимальной

A e_t -^max ;

после    максимальной

- Aet —> min.

точки:

точки:

точки:

Для параметров T_pea:

ячейка 61: т -pea -^ min , Tpea1 "^ min, т   - pea2 > min ; ячейка 62: т -pea max ,   peal ' max , Tpea2 " -> max; ячейка 63: т -pea -> min , Tpea1 - > min , Tpea2 ^ min; ячейка 64: т - pea -> max , Tpea1 - > max , Tpea2 - -^ max. Для расчета введенных парамет- ров можно воспользоваться формулой (4)

T pea = T pea 1 + T pea 2 = ^T ct 2 ^{_ T}ct 1 =

( Tptmax   Tct 1) + ( Tct2   Tptmax), где: Tpea 1, Tptmax и др. координаты соответствующих точек на ось t.

В строке 7 представлены варианты изменения переменные et и pt, в виде двух кривых, имеющих максимумы и пересекающиеся в двух точках. Здесь в ячейках 71 и 72 их максимумы расположены на одной прямой, а в ячейках 73 и 74 смещены относительно друг друга на величину Tpxex (ячейка 73) или на Tepx (ячейка 74). В данном варианте должны быть следующие значения рассматриваемых параметров.

Для параметров A e t и A p t :

• •    ячейки 71, 72, 73 и 74: до точек T_ep и T_bp: ete_t —> max , Ap_t —> min ; после точек T_ep и T bp : - A e t -> min - pp_t —> max .

Для параметров T epx и T pex :

• •    ячейки 71 и 73: T_x —» min ; ячейки pex

72 и 74: Г   —> max .

epx

Для параметров T expx и T pxex :

• •    ячейка 73:   при    T bet    >T b _pt ,

T pxex ~+ ^max ; при T bet <  T bpt , T expx -> min •

• •    ячейка 74:  при   T bet   >   T bpt ,

T pxex -^ min ; при T bet <  T bpt , T expx -^ max .

Для параметров Q expx и Q pxex :

населением страны

• •    ячейки 71 и 73: Q  -> min ;

• •    ячейки 72 и 74: Q  -> max .

В строке 8 показаны варианты изме- нения переменные et и pt, которые представляют собой две кривые, имеющие мак- симумы и минимумы и пересекающиеся в двух точках. При этом в ячейках 81 и 82 их максимумы и минимумы расположены на одной прямой, а в ячейках 83 и 84 смещены относительно друг друга на величины Tpxex и Texpx соответственно. В этом случае должны быть следующие значения рассматриваемых параметров.

Для параметров A e t и A p t :

• •    ячейки 81 и 83: до точек T ep и T_bp: e e_t —> max , - pp_t -^ max ; после точек T _ep и T_bp: — ee, —> min , i\p_t -^min .

• •    ячейки 82 и 84: до точек T ep и T_bp: — A e_t —> min , Zxp_t —> min ; после точек T_ep и T bp : A e_r —> max , - pp_t —> max .

Для параметров T epx и T pex :

• •    ячейки 81 и 83: T  m-max ;

pex ячейки 82 и 84: T  —> min .

epx

Для параметров T enpx и T pnex.

• •    ячейка 83:   при    T bet    >T bpt ,

T pnex "^ max ;            при T bet <  T bpt ,

T pnex ~> max .

• •    ячейка   84:   при    T bet    >T bpt ,

^Tenpx "^ min ; при T bet <  T bpt , T enpx ^ min .

Для параметров Q pxen и Q expn" : ячейки 81 и 83: Q mmax ; ячейки 82 и 84: expn

^Q pxen -> min .

Если теперь построить графики переменных e t и p t за определенный промежуток времени, то они могут быть четырех видов (рис. 2).

Взяв за основу рис. 2 можно все страны разбить на четыре класса:

• к ласс экономически и промышленно развитых стран (рис. 2 a );

• к ласс слаборазвитых и развивающихся стран (рис. 2 b );

класс стран с неустойчивой экономикой, когда имеются площади с отрицательным значением Septц.) и Spet1(.) (рис. 2c, d);

класс стран переходного периода, когда площади S ept и S_pet равны нулю, т.е. S ept = S pet = 0. Это графики, где переменные e_t и p t сольются. Значения S ept = S_pet = 0 представляют собой частный случай, следовательно, целесообразно принять, что к странам переходного периода будут относиться, например, такие страны, у которых значения Q_et = f_e ( t ) отличаются от значений Q_pt = f_p ( t ) на ±5%.

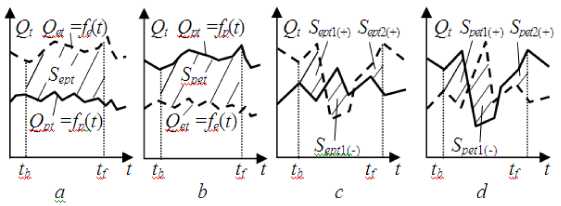
Рисунок 2 - Площади: a - страны с развитой экономикой; b страны со слаборазвитой и развивающейся экономикой; c, d - страны с неустойчивой экономикой

Кроме того, здесь следует отметить, что со временем слаборазвитые страны могут перейти в группу развитых стран. Но здесь следует сразу оговориться, что к развитым странам будем относить такие, где развита промышленность и наукоемкое производство. Но есть страны, например ряд стран Персидского залива, чье экономическое богатство высоко за счет добываемой нефти и газа, но отнести их к высокоразвитым странам нельзя.

Для стран с развитой экономикой теоретическую площадь S ept рассчитывается по формуле (5)

tf                           tf

Sept = Stet-St,, = ff. (t) dt- ff, (t )dt = ... tb                       tb tf

...= J(. f e ( t )" f, ( t )) dt , ед 2 .               (5)

tb

Для слаборазвитых и развивающихся стран при расчете площади S pet следует воспользоваться формулой (6)

tf                            tf

Spet = Sp - S„t = Vt ( t ) dt - $Л ( tW= ...

tb                         tb tf

...= R f p ( t )- f e ( t )) dt , ед² .              (6)

tb

Если же рассматриваются страны с неустойчивой экономикой, то в этом случае следует воспользоваться следующими двумя формулами (7) и (8) в зависимости от конкретных условий.

"" ^ S epti (+)   ^ ^Septj (-) , ед .

i ⁼¹                  j ⁼¹

Z S„;„- ZS„H, ед2 (8)

i =1 j =1

Основываясь на представленной выше таблице и описания вариантов была разработана классификация зависимостей переменных e t и p t , которая изображена на рис. 3. Как видно из рис. 3 переменные e_t и p_t можно разбить на три класса: класс линейных зависимостей, класс линейных и криволинейных зависимостей и класс криволинейных зависимостей. Эти классы в свою очередь подразделяются на три подкласса: увеличивающиеся, уменьшающиеся, увеличивающиеся и уменьшающиеся.

Подклассы разбиваются на пять следующих видов: сливающиеся, несли-вающиеся, расходящиеся и т.д. Эти виды сами разбиваются на пять подвидов, в зависимости от рассматриваемого вида, такие как: параллельные, непараллельные и т.п. И на последнем уровне переменные e_t и p_t разбиваются на два типа в зависимости от того закона или законам, по которым они изменяются.

Выше были рассмотрены варианты с учетом того, чтобы благосостояние населения имело максимальное значение и поэтому принимались следующие значения переменной p_t : pp_t —> min и - Рр_t -> max , что справедливо для стран с переизбытком населения, таких как Китай и Индия. Но если исходить из того, что во многих евро-

Возможные направления развития экономики при кризисе и росте в взаимосвязи с населением страны пейских, скандинавских и других стран проблемы с ростом населения, то в этом случае значения переменной pt должны быть следующими: p min и p max .

Данная классификация позволяет быстро определить конкретные рассматриваемые переменные e t и p t к их классу, подклассу и т.д. и определить возможные варианты развития, как экономики, так и населения страны в ближайший промежуток времени.

Показанную выше классификацию на рис. 3 можно представить в виде графа, изображенного на рис. 4, где вершинами графа являются линейные, криволинейные или их комбинации зависимости, которые могут увеличиваться или уменьшаться, симметричными и т.д., а ветвями их характеристики. Таким образом, чем больше мы будем знать параметры характеристик ветвей вершин, тем проще будет сделать правильные выводы при анализе экономического состояния

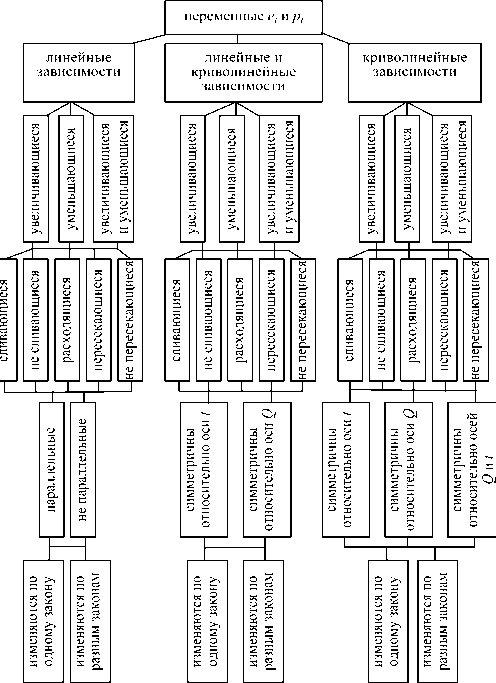
Рисунок 3 - Классификация зависимостей

государства и его населения.