Возможный подход для оценки систем молниезащит ракет-носителей на космодромах

стенок камеры. Результаты численных расчётов в 3-х мерном пространстве позволили объяснить известные экспериментальные данные о концентрации ударных волн, образующихся при мощном электрическом разряде в жидкости [6], причём они принципиально отличны от [7], трактующей процессы на основе эмпирических зависимостей. В дальнейшем эти процессы дополнительно исследовались в [8] с применением метода инверсии для полубесконечных областей (МИПО).

Для определения электромагнитных полей молнии в [2] показаны существующие основные подходы: 1) на основе численных решений точных уравнений с помощью специализированных алгоритмов; 2) численных решений уравнений Максвелла на базе, например, метода конечных разностей во временной области (finite-difference timedomain method – FDTD); 3) с использованием упрощённых уравнений. Отмечается, что если ранее FDTD использовался для анализа перенапряжений, индуцированных в линиях передач разрядом молнии, то в настоящее время применяется для анализа электромагнитных полей молнии.

В целом представленные в обзоре [2] математические модели – это в настоящее время основные модели для исследования разряда молнии и её различных физических проявлений, однако для оценки и сравнительного анализа существующих важных технических решений, например, в виде систем молниезащит ракет-носителей на космодромах [9], необходимы разработки дополнительных математических моделей.

Постановка задачи. Схема расположения типичной системы молниезащиты из 4-х молние-приёмников (рис. 1) для ракет-носителей с космическими аппаратами характерна для стран США (космодром на мысе Канаверал, Флорида), Франции, Индии и др. [9]. Для упрощения исследований представим систему молниезащиты ракеты-носителя в виде башен с металлическими стержнями на их вершинах (например, не учитываются тросы, расположенные на вершинах стержней молниезащиты по контуру, особенности этих стержней, их материал и др.). Устройство 5 (рис.

1), связанное с ракетой-носителем на старте, представляется в виде металлической фермы, например, как на стартовой площадке №40 космодрома на мысе Канаверал для ракет-носителей типа «Falcon 9» для запуска космических аппаратов SpaceX Dragon.

А1	А2 5
А3	А4

Рис. 1. Схема типичной системы молниезащиты на космодроме: 1 – 4 – башни с цилиндрическими стержнями; 5 – ферма

При математическом моделировании системы молниезащиты на стартовой площадке применяется схема, показанная на рис. 2. Для учёта влияния дистанции l ₁ от металлической фермы 5 до башни со стержнем 1 исследования проводятся в вертикальной диагональной плоскости от 1-ой до 4-ой башни. Границы области B ( x , y ) следующие: G₁ – плоскость в виде поверхности земли F ( x,y ); G₂ – нижняя граница облака V ( x, y ) в виде плоскости относительно поверхности F ( x,y ); G 3 , G 4 – границы для искусственного ограничения расчетной области путём введения в постановку задачи граничного условия типа ∂ψ/∂ n = 0, так как в этой задаче не учитывается краевой эффект от V ( x,y ).

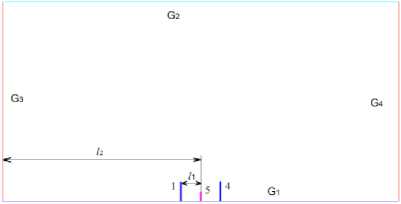
Рис. 2. Схема моделирования области B ( x , y ) системы молниезащиты на космодроме (цифровые обозначения как на рис. 1)

В [10, 11] было проведено сравнение результатов расчета внешней краевой задачи с учётом краевого эффекта от облака и заземлённого стержня на основе МИПО с данными [12] в вертикальной плоскости по распределению поля ψ. В [12] решалась задача определения поля потенциала ψ, и также были введены облако и стержень, но внешняя краевая задача была сведена к внутренней на основе условия ∂ψ/∂ n =0. Погрешность была незначительная для исследуемой части области, при этом в [11] были показаны особенности исследуемого краевого эффекта. В связи с этим исходные данные для расчёта следующие: 1) расстояние от металлической фермы 5 до границы G₃ считается l ₂

= 1000 м; 2) высота от F ( x,y ) до нижней границы V ( x, y ) принимается H ₁ = 1000 м; 3) высота башней со стержнями считается H ₂ = 100 м; 4) высота металлической фермы принимается H 3 = 50 м; 5) дистанция l 1 = var .

Для представления особенностей плоского или плоскопараллельного электростатического необходимо определить эквипотенциальные поверхности с шагом Δψ = const и поверхности электрической функции потока µ с шагом Δµ= const [13]. Как и потенциал ψ функция µ является относительной характеристикой поля, причём физический смысл имеет только разность её значений например, в точках p, d и не зависит от формы кривой и определяется в виде:

p

µ p – µ d = ∫ Endl .             (1)

d

Здесь E_n – проекция напряженности поля по нормали к кривой.

Следует заметить, что вектор напряженности поля E направлен по касательной к силовой линии (поверхности), поэтому линейный поток напряженности поля через любой отрезок силовой линии равен нулю. В связи с этим точки силовой линии характеризуются одним значением функции потока, причём каждая силовая линия в плоскопараллельном поле – это линия (поверхность) функции потока µ с уравнением вида

µ i = const .                         (2)

Приращение потенциала dψ на длине dn связано зависимостью dψ = – Ek dn.                  (3)

Здесь знак «–» означает, что падение ψ происходит в направлении силовой линии. По определению функции потока её приращение dµ на длине dl равно dµ = Ekdl.                       (4)

С учётом зависимостей (3), (4) величина E может определяется в виде

E k = – d ψ / dn и E k = d µ / dl.          (5)

Следовательно, напряженность поля равна падению потенциала на единицу длины в направлении силовой линии или увеличению функции потока на единицу длины в направлении эквипотенциальной линии. Эти соотношения необходимы при решении задачи о распределении µ. Для оценки и сравнительного анализа существующих технических решений систем молниезащит ракет-носителей на стартовых пло-щадках предлагается решение задачи в два этапа.

Первый этап. Определяется поле распределения потенциала ψ на основе решения уравнения Лапласа в виде

• □ д у /д x ² + д у /бу 2 ; ( x,у ) е B(x,у ).              (6)

Граничные условия задачи c учётом рис. 2 следующие:

• •    на границе G₁:

V(x,y)=0, (x,y) e Gi;(7)

• •    на границах башен со стержнями 1 (G₁₁), 4 (G₁₄) и на металлической ферме 5 (G₁₅) заземлённых относительно F ( xy ):

V(x,y)=0, (x,y) e Gii, G14, G15;(8)

• •    на границах G₃, G₄:

d^/5n=0, (x,y) e G3, G4;(9)

• •    на границе G₂:

V(x,y)=Vo, (x,y) e G2;(10)

где B ( x , y ) - исследуемая область, ограниченная G₁ - G 4 , G 11 , G 14 , G 15 .

Считаем, что на G₂ потенциал равен у₀ при возникновении электрических полей в атмосфере. При этом исследуется электростатическое поле при условии, что внешнее поле, прикладываемое к объектам 1-5, существенно мало, т.е. подразумевается отсутствие объёмных электрических зарядов в атмосфере исследуемой области B ( x , y ). При решении задачи определяются поле ψ и эквипотенциальные поверхности у i = const с некоторым шагом А^= const . Затем относи-тельно высоты H ₁ на основе расчётов этого этапа выделяется некоторая область D ( x , y ) до уровня Н ₄ относительно поверхности F ( x, y ) с учётом симметрии в области B ( x , y ) относительно 5.

Рис. 3. Схема моделирования области D ( x , y ) системы молниезащиты (цифровые обозначения как на рис. 1)

Особенность выбора D ( x , y ) следующая: 1) на уровне Н ₄ поверхность у k = const должна быть параллельна границе G₂, чтобы было исключено влияние системы молниезащиты на распределение напряженности поля на этом уровне; 2) H 4 должна превышать max высоту H ₂ объектов 1 - 4 системы молниезащиты.

Второй этап. Схема моделирования области D ( x , y ) системы молниезащиты на космодроме, показана на рис. 3. Границы исследуемой области D ( x , y ) следующие: G 21 - граница в виде части G 1 ; G 22 - граница на уровне H 4 в виде некоторой поверхность у k = const ; G₃₁ - граница в виде части G₃; G₄₁ - граница в виде части симметрии области B ( x , y ), проходящая через объект 5; G₁₁, G₁₅ - границы соответствующие области B ( x , y ).

Исходные данные для расчёта следующие: 1) расстояние от металлической фермы 5 до границы G31 считается 13 = 200 м; 2) высота от F(x,y) до поверхности уk=const равна H4 (будет определена после расчетов первого этапа); 3) высота башни со стержнем H2=100 м; 4) высота металлической фермы H3=50 м; 5) дистанция 11=var. Поле распределения электрической функции потока ц определяется из эллиптического уравнения аналогичному урав- нению Лапласа:

• □    дц /дx2 + дц /dy2; (x,y) e D(x,y).(11)

Граничные условия задачи c учётом рис. 3 следующие:

• •    на границе G 21 :

дц/дn=0, (x,y) e G21;(12)

• •    на границах башни со стержнем 1 (G 11 ) и на металлической ферме 5 (G₁₅):

дц/дn=0, (x,y) e Gn, G15;(13)

• •    на границе G₃₁:

ц(x,y)=ц 0, (x,y) e G31;(14)

• •    на границе G₄₁:

ц(x,y)=0, (x,y) e G41;(15)

• •    на границе G 22 :

ц(x,y)=0, (x,y) e G22;(16)

где D ( x , y ) - исследуемая область, ограниченная G₂₁, G₃₁, G₄₁, G₂₂, G₁₁, G₁₅.

Для оценки и сравнительного анализа системы молниезащиты на космодроме считаем, что появление молнии возможно, например, со стороны границы G₂₂, а именно, её левого края. Тогда на этой части границы G 22 , а именно, на границе G 23 выполняется условие:

дц/д n =0, ( x , y ) e G₂₃. (17)

Особенности дискретных математических моделей каждого этапа расчёта заключаются в том, что исходные области B(x,y) и D(x,y) представляются дискретными с регулярной прямоугольной сеткой (Ax=Ау) по аналогии, например, [10]. При расчетах не учитываются размеры в горизонтальных сечениях элементов систем молниезащит 1-4 и металлической фермы 5, так как они пренебрежимо малы по сравнению с шагом Δ сетки по координатам x, у (по поверхности F(xy) между G3 и G4 расстояние 2000 м, а H1=1000 м, при этом считаем, что в горизонтальном сечении металлическая ферма имеет размеры 4,0 х 3,0 м2).

Для каждой из областей B ( x , у ) и D ( x , у ) во внутренних узлах сетки выполняется условие сходимости итерационного метода Гаусса-Зейделя. В этих узлах дискретных областей потенциал у i,■ рассчитывается с помощью числен-ного метода, например, ускоренного метода Либмана с учётом уравнения Лапласа в конечно-разностных аппроксимациях как в [10]. На границах G i областей B ( x , у ) и D ( x , у ) потенциалы у i,■ рассчитываются с учетом конечно-раз-ностных аппроксимаций на основе условий: 1) для области B ( x , у ) используются граничные условия (7)-(10); 2) для области D ( x , у ) соответственно граничные условия (12)-(17).

Результаты численных расчетов. При исследованиях на первом этапе существующих технических решений систем молниезащит ракет-носителей на космодромах в области B ( x , у ) определяются поля распределения потенциала ψ и эквипотенциальные поверхности в виде уравнений у i = const . Расчёты ведутся в безразмерном виде, а именно, потенциалы у i =^ i /^₀; где у₀ — базовое значения потенциала в исследуемой области. Аналогично записываются безразмерные параметры и для других величин. Результаты численного расчета согласно уравнениям (6)-(10) для схемы моделирования области B ( x , у ) системы молниезащиты, показаны на рис. 4 в виде распределения эквипотенциальных поверхностей у i = const с А^ = const.

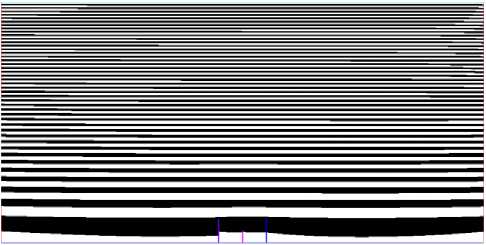
Рис. 4. Распределение эквипотенциальных поверхностей для^исследуемой области B ( x , у ) в виде у i = const с Ау = const

Последующая схема для математического моделирования области D ( x , у ) с учётом системы молниезащиты на космодроме, показана на рис. 3. На основе полученных результатов величина H ₄ выбирается равной 500 м.

А1. Для оценки и сравнительного анализа технического решения системы молниезащиты ракеты-носителя на космодроме (см. рис. 1) принимается дистанция 1 1 от металлической фермы 5 до башни со стержнем 1 равной 200 м, т.е. элемент молниезащиты находится на границе G 31 области

D ( x , у ). Для исследования предлагаемого подхода на основе 2-х этапов считаем, что появление молнии возможно, например, со стороны границы G₂₂, а именно, её левого края границы G₂₃. Результаты численного расчета согласно уравнениям (11)-(17) для схемы моделирования области D ( x , у ), показаны на рис. 5 в виде распределения поверхностей электрической функции потока р i = const с шагом Ар = const. При этом на рис. 5а показаны 30 функций потока р i ; рис. 5б соответственно 100 функций потока р i .

а)                        б)

Рис. 5. Распределение поверхности электричес-кой функции потока р i = const с шагом Ар = const при l 1 = 200 м

Из результатов, представленных на рис. 5б, следует: 1) в объект 5 входят 19 функций потока р i и одна частично в объект 5 и в поверхность F ( x,y ); 2) в поверхность F ( x,y ) входят 38 функций потока р i ; 3) в элемент молниезащиты 1 входят 41

функция потока р i и одна частично в элемент 1 и в F ( x A).

А2. Принимается дистанция l 1 от металлической фермы 5 до башни со стержнем 1 равной 100 м, т.е. элемент молниезащиты находится по средине между границей G 31 и объектом 5 области D ( x , у ). Результаты численного расчета для этой схемы моделирования области D ( x , у ) с учётом 1 1 =100 м, показаны на рис. 6 в виде распределения поверхностей электрической функции потока р i = const с шагом Ар = const. При этом на рис. 6а показаны 30 функций потока р^; рис. 6б соответственно 100 функций потока р i .

Из результатов, представленных на рис. 6б, следует: 1) в объект 5 входят 11 функций потока рi и одна частично в объект 5 и в поверхность F(x,y); 2) в поверхность F(x,y) входят 5 функций потока цi*; 3) в элемент молниезащиты 1 входят 71 функция потока цi и 2 частично в элемент 1 и в поверхность F(xy), т.е. справа и слева от элемента 1.

а)                          б)

Рис. 6. Распределение поверхности электричес-кой функции потока ц i = const с шагом Ац = const при 1 1 =100м

а)                         б)

Рис. 7. Распределение поверхности электричес-кой функции потока ц i = const с шагом Ац = const при 1 1 =50м

А3. Принимается дистанция 1 1 от металлической фермы 5 до башни со стержнем 1 равной 50 м. Результаты численного расчета для схемы моделирования области D ( x , y ) с учётом 1 1 =50 м, показаны на рис. 7 в виде распределения поверхностей электрической функции потока ц i = const с шагом Ац = const. При этом на рис. 7а показаны 30 функций потока ц i ; рис. 7б соответственно 100 функций потока ц i .

Из результатов, представленных на рис. 7б, следует: 1) в объект 5 входят 3 функций потока ц i и одна частично в объект 5, в поверхность F ( xy ) и в элемент молниезащиты 1; 2) в поверхность F ( xy ) перед объектом 5 входит одна функция потока ц i частично в объект 5, в поверхность F ( x, y ) и в элемент молниезащиты 1 и 25 после элемента молниезащиты 1; 3) в элемент молниезащиты 1 входят 69 функция потока ц i и 1 частично в элемент 1 и в поверхность F ( xy ).

Сравнительный анализ технического решения системы молниезащиты на космодроме (см. рис. 1) показывает следующее: 1) при дистанции 1 1 =200 м в объект 5 в целом входят 19 функций потока ц i и одна частично, тогда относительная величина входа функций потока ц i в объект 5 в процентах равна 20%; 2) при 1 1 =100 м в объект 5 входят 11 функций потока ц i и одна частично, тогда относительная величина входа функций потока ц i в объект 5 в процентах равна 12%; 3) при 1 1 = 50 м в объект 5 входят 3 функций потока ц i и одна частично, тогда относительная величина входа функций потока ц i в объект 5 в процентах равна 4%. В заключение отметим, что для типичной системы из 4-х элементов молниезащиты ракеты-носителя с космическим аппаратом согласно распределению электрической функции потока ц i при уменьшении дистанции 1 ₁ с 200 до 50 м относительная величина входа функций ц i в объект 5 уменьшается с 20 до 4%.

Выводы:

• 1.    Анализ полученных результатов расчёта на основе предложенного подхода показал, что имеется возможность оценивать и выявлять особенности системы из 4-х элементов молниезащиты на космодроме. Например, установлено, что согласно распределению электрической функции потока ц i при уменьшении дистанции 1 ₁ в 4 раза, относительная величина входа функций ц i  в объект 5

• 2.    Показаны особенности предложенного подхода для численного моделирования исследуемой системы молниезащиты на космодроме в два этапа. На первом этапе решения задачи определяются поле распределения потенциала у и эквипотенциальные поверхности у i = const с А^ = const . Затем относительно высоты H на основе расчётов этого этапа выделяется некоторая область D ( x , y ) до уровня Н ₄ относительно поверхности земли F ( xy ). На втором этапе определяется распределение поверхностей электрической функции потока ц i = const с шагом Ац = const при изменении,

• 3.    Представлены особенности выбора области D ( x , y ) в следующем виде: 1) на уровне H 4 выделенная поверхность ψ _k = const должна быть параллельна границе G 2 , чтобы было исключено влияние системы молниезащиты на распределение напряженности поля на этом уровне; 2) H 4 должна превышать max высоту H 2 объектов 1-4 системы мол-ниезащиты.

уменьшается в 5 раз. Полученные результаты и выводы определяются соотношениями размеров исследуемой системы молниезащиты и соответствующими допущениями при расчётах.

например, дистанции l 1 от металлической фермы 5 до башни со стержнем 1.