Возмущенная магнитосфера 7-8 ноября 2004 г. и вариации жесткости обрезания космических лучей: широтные эффекты

Геомагнитное поле разрешает или запрещает приход частиц космических лучей (КЛ) в данную точку в магнитосфере и атмосфере в зависимости от их энергии. Самая низкая широта, до которой энергичные частицы могут проникать, известна как широта обрезания. Эта широта является функцией жесткости обрезания (момент на единицу заряда). Жесткость R геомагнитного обрезания — пороговая жесткость, ниже которой поток частиц равен нулю из-за геомагнитного экранирования. Распределение по широте и долготе жесткости обрезания определяется пространственной структурой и интенсивностью магнитосферного магнитного поля, которое меняет направление движения КЛ. Свойства магнитного экрана сильно меняются во времени в зависимости от динамического взаимодействия магнитных и электрических полей солнечного ветра с внутри-магнитосферными полями и токами. Особенно значительные изменения в токах, плазме и магнитном поле магнитосферы происходят во время геомагнитной бури [Leske et al., 2001] .

Знание распределения изменений жесткостей обрезания КЛ Δ R в течение магнитной бури становится все более актуальным для учета последствий плохой космической погоды для космонавтики и бурно развивающихся в последние 15 лет высокоширотных авиаперевозок [Iucci et al., 2005; Буров и др., 2005; Kress et al., 2015] . Долготные и широтные зависимости вариаций жесткостей обрезания в спокойные периоды и во время отдельных магнитных бурь рассматривались в ряде статей [Dorman, 1963; Flueckiger et al., 1987; Antonova et al., 1990; Belov et al., 2005; Dvornikov et al., 2009; Данилова и др., 2019] . Однако широтные зависимости чувствительности жесткостей обрезания к различным параметрам магнитосферы оставались за рамками этих исследований.

В данной работе мы провели исследование широтной зависимости Δ R , а также широтных эффектов в корреляции Δ R с изменениями межпланетного магнитного поля (ММП) и геомагнитной активности для бури 7–8 ноября 2004 г. Связь вариаций жесткостей обрезания с параметрами магнитосферы на интервале всего магнитосферного возмущения 7–11 ноября 2004 г. и отдельно в период первой бури 7– 8 ноября рассматривалась в наших работах [Tyasto et al., 2013; Птицына и др., 2019]. Новым аспектом данного исследования является то, что мы остановились на анализе именно широтных эффектов, причем во время каждой из трех фаз бури: на предварительном этапе, на главной и восстановительной фазах бури 7–8 ноября.

МЕТОДЫ И ДАННЫЕ

Вариации жесткостей обрезания ΔR были вычислены при помощи наблюдательного метода спектрографической глобальной съемки, в котором жесткости обрезания Rсгс определяются по наблюдательным данным сети нейтронных мониторов, и который подробно описан в [Dvornikov et al., 2013], и модельного метода, в котором для определения жесткостей обрезания Rэф численно рассчитываются траектории частиц в модельном магнитном поле магнитосферы [Shea et al., 1965]. Мы использовали магнитосферную модель Ts01 [Tsyganenko et al., 2003] для сильных магнитных возмущений, о чем подробно писали авторы в более ранних работах (например [Tyasto et al., 2013]).

Δ R _э ф и Δ R _сгс определялись как разности между значениями геомагнитных порогов, рассчитанными для каждого часа в период бури, и значениями в спокойный период 6 ноября 2004 г. Выбор спокойного периода обусловлен тем, что в это время электромагнитная обстановка в межпланетном пространстве и геомагнитная обстановка были спокойными, а спектр галактических КЛ наименее модулирован.

Коэффициенты корреляции k между жесткостями обрезания и параметрами ММП вычислялись для следующих станций: Токио (35.75° N, 139.72° E), Алматы (43.20° N, 76.94° E), Рим (41.90° N, 12.52° E), Иркутск (52.47° N, 104.03° E), Москва (55.47° N, 37.32°E) и Хобарт (42.90° S, 147.33° E). Станции выбирались таким образом, чтобы они в спокойное время охватывали основную область пороговых жесткостей R _c, подверженных влиянию геомагнитного поля: Токио — 11.0 ГВ, Алматы — 6.18 ГВ, Рим — 6.10 ГВ, Иркутск — 3.25 ГВ, Москва — 2.12 ГВ, Хобарт — 1.76 ГВ. Пороговые жесткости станций R c рассчитывались как среднее за спокойные сутки 6 ноября 2004 г.

При вычислении наблюдательных изменений пороговых жесткостей геомагнитного обрезания использовались данные мировой сети станций КЛ [].

Коэффициенты корреляции k и стандартные ошибки получены из анализа регрессионных уравнений отдельно по выборкам наблюдений для периодов каждой из трех фаз — предварительной, главной и восстановительной.

Данные о параметрах ММП и геомагнитной активности взяты на сайте [ gov/form/].

С учетом особенностей развития бури [Ермолаев и др., 2014; T surutani et al., 2008] ее можно разбить на три фазы: предварительная, т. е. период перед бурей с 03:00 по 19:00 UT 7 ноября, главная с 20:00 UT 7 ноября по 06:00 UT 8 ноября, фаза восстановления с 07:00 по 24:00 UT 8 ноября.

РЕЗУЛЬТАТЫ

На рис. 1 показаны примеры широтного поведения вариаций геомагнитных порогов Δ R _сгс и Δ R _э ф в зависимости от пороговых жесткостей R _с используемых станций для нескольких моментов времени в течение бури. Видно, что во время предварительной фазы в момент, когда Dst = 7 нТл, жесткость R сгс (панель а ) не меняется с широтой (или жесткостью станции). Для главной и восстановительной фаз широтная кривая принимает типичную форму с максимумом падения жесткости обрезания на среднеширотных станциях [Dorman, 1963; Flueckiger et al., 1987; Dvornikov et al., 2009] . При этом максимум на главной фазе достигается при R c ≈ 3 ГВ, а на восстановительной он сдвигается к R c ≈ 6÷7 ГВ, т. е к более низким широтам.

Видно ( б ), что на предварительной фазе Δ R _э ф , так же как и Δ R _сгс, практически не меняется с широтой. На главной и восстановительной фазах широтные зави-

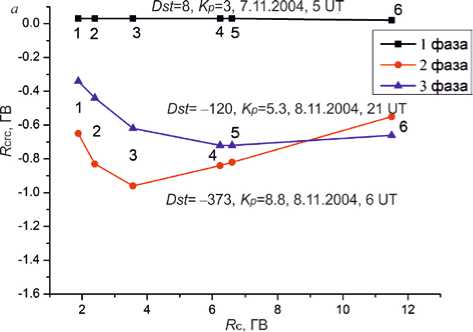
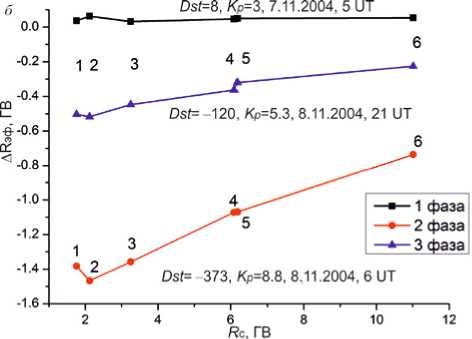
Рис. 1. Изменения ΔRсгс (а) и ΔRэф (б) в зависимости от пороговой жесткости станции Rс для различных фаз бури: 1 фаза — предварительной, 2 фаза — главной, 3 фаза — восстановительной. Станции обозначены в порядке убывания широты: 1 — Хобарт, 2 — Москва, 3 — Иркутск, 4 — Рим, 5 — Алматы, 6 — Токио симости ΔRэф отличаются от широтных зависимостей ΔRсгс главным образом тем, что не показывают характерной кривой с максимумом падения жесткостей на средних широтах. На главной и восстановительной фазах наблюдается монотонный рост ΔRэф с увеличением пороговой жесткости станции, т. е. с уменьшением широты станций, с неявным максимумом при Rc ≈ 2 ГВ. Наибольшее расхождение кривых ΔRсгс(Rс) и ΔRэф(Rс) наблюдается на восстановительной фазе. На главной фазе для Rс ≥ 3 ГВ поведение кривой ΔRсгс(Rс) аналогично поведению ΔRэф(Rс), но наблюдается значительная разница в величине ΔR. Сравнение панелей а, б показывает, что на главной фазе при достижении максимума бури (Dst = –373 нТл), максимальное падение жесткости ΔRэф= –1.5 ГВ, что в полтора раза больше, чем ΔRсгс = –0.96 ГВ. Такая значительная разница не отмечается для предварительной и восстановительной фаз. Следует отметить, что в обоих случаях видно, что падение жесткости в зависимости от широты (или Rс) усиливается с увеличением │Dst│.

С учетом этих результатов дальнейшее исследование мы провели для наблюдательных значений ΔRсгс, а также остановились только на главной и восстановительной фазах бури. Мы вычислили коэффициенты корреляции k между значениями ΔRсгс и параметрами ММП и геомагнитной активности для главной фазы и фазы восстановления на шести выбранных для исследования станциях и проследили эти взаимосвязи в зависимости от пороговой жесткости станций. Коэффициенты k и стандартная ошибка регрессии σ представлены в таблице.

На рис. 2 показаны коэффициенты k между значениями Δ R сгс и Dst , K p , B y , и B z в зависимости от станции наблюдения для главной и восстановительной фаз. Они показывают интересные особенности. Корреляция Δ R _сгс и Dst растет а Δ R _сгс и B_y падает с уменьшением пороговой жесткости станции. Таким образом, широтная зависимость k для связи Δ R сгс и Dst зеркально повторяет широтную кривую k для связи Δ R _сгс и B_{y .} Широтная зависимость k для связи с K p зеркально повторяет широтную кривую k для связи с B_z . Наиболее ярко эта картина проявляется для фазы восстановления (панель б ). Для этого периода широтная кривая k для связи Δ R _сгс и Dst практически совпадает с широтной кривой | k | для связи с B y . Аналогично широтная кривая k для связи с K _p практически совпадает с широтной кривой | k | для B_y . Кроме того, на фазе восстановления k между Δ R сгс и Dst растет с увеличением широты станции, в то время как изменения корреляции между Δ R _сгс и K _p носят более сложный характер. На главной фазе зависимость корреляции Δ R _сгс и K _p от пороговой жесткости станции представляет собой слабовыра-женную волну, которая находится в противофазе с аналогичной волной для k между Δ R _сгс и B_z .

Исходя из результатов, представленных на рис. 2, можно предположить, что во время исследуемой бури поведение Dst контролировалось в большой степени B y -компонентой ММП, а K p — B z -компонентой. Чтобы проверить это предположение, мы провели корреляционный анализ между параметрами ММП и индексами геомагнитной активности на разных фазах бури, результаты которого показаны на рис. 3.

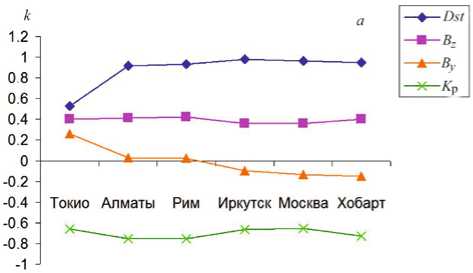
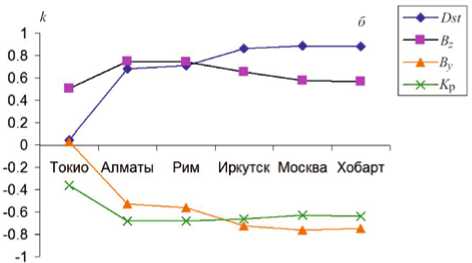
Рис. 2. Широтная зависимость коэффициентов корреляции k между ΔRсгс и параметрами ММП и геомагнитной активности для главной фазы бури (а) и фазы восстановления (б). Станции идут в порядке возрастания широты

Коэффициенты корреляции значений Δ R _сгс и Dst , K_p , B_{y ,} B_z в зависимости от станции наблюдения для главной и восстановительной фаз

	главная фаза/восстановительная фаза
	Dst	σ	B z	σ	B y	σ	K p	σ
Токио	0.53/0.05	0.14/0.14	0.40/0.50	0.15/0.12	0.26/0.03	0.16/0.14	-0.66/-0.36	0.13/0.13
Алматы	0.92/0.68	0.10/0.12	0.42/0.75	0.22/0.11	0.03/-0.53	0.24/0.14	-0.75/-0.68	0.16/0.12
Рим	0.93/0.71	0.09/0.12	0.43/0.74	0.23/0.12	0.03/-0.56	0.25/0.15	-0.75/-0.68	0.17/0.13
Иркутск	0.97/0.86	0.08/0.12	0.36/0.65	0.31/0.18	-0.10/-0.72	0.33/0.17	-0.67/-0.66	0.25/0.18
Москва	0.97/0.89	0.08/0.09	0.36/0.58	0.28/0.17	-0.13/-0.76	0.30/0.13	-0.66/-0.63	0.23/0.16
Хобарт	0.95/0.88	0.07/0.06	0.40/0.57	0.21/0.10	-0.15/-0.75	0.22/0.09	-0.73/-0.64	0.16/0.10

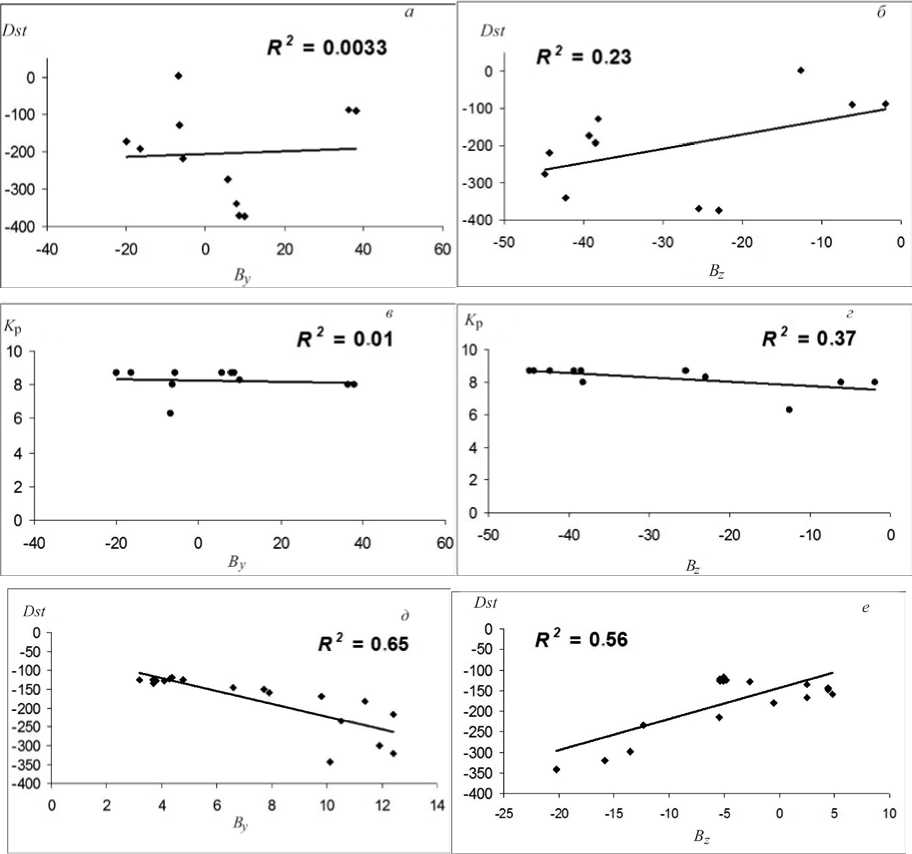
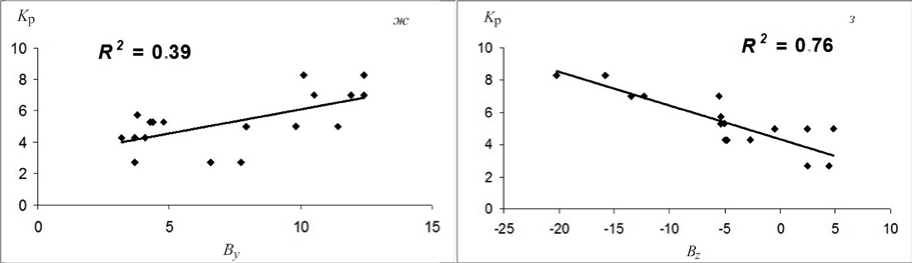
Рис. 3. Диаграммы рассеяния для главной ( а – г ) и восстановительной фаз бури ( е – з ). Линейный тренд показан прямой линией, R ² — достоверность аппроксимации

Диаграммы рассеяния для главной фазы ( а – г ) показывают, что корреляция между индексами геомагнитной активности ( Dst и K p ) и компонентами ММП ( B y , B z ) сравнительно низкая. Отметим, что, хотя видна достаточно заметная корреляция ( б ) между Dst и B_z (0.46), точки на диаграммах рассеяния для Dst ( а , б ) расположены хаотично. Лишь диаграммы рассеяния ( г ) показывают существенную зависимость K _p от B_z (-0.60). В период восстановления связь между K p и B z усиливается. Видно, что в период восстановления ( д – з ) коэффициенты корреляции как между K _p и B_z (0.87), так и между Dst и B_y (0.81) высоки. Однако корреляция между Dst и B z (0.75), а также между K p и B y (0.62) несколько меньше.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Для главной и восстановительной фаз исследуемой магнитной бури широтная кривая Δ R сгс ( R с ) принимает классическую форму с максимумом падения жесткости обрезания на среднеширотных станциях. При этом максимум падения жесткостей на главной фазе достигается при R с ≈ 3 ГВ, что в целом совпадает с обычно наблюдаемой картиной. На восстановительной фазе максимум сдвигается к R с ≈ 6÷7 ГВ, т. е. к более низким широтам. Это значение R с , при котором наблюдается максимум падения жесткостей, близко к R с ≈ 7÷8 ГВ, полученной для очень сильной бури в ноябре 2003 г. [Belov et al., 2005] . Широтные зависимости модельных Δ R эф ( R с ) отличаются от широтных зависимостей наблюдательных Δ R сгс ( R с ) по величине. Кроме того, они не представляют характерной кривой с максимумом падения жесткостей на среднеширотных станциях. В работе [Belov et al., 2005] при исследовании бури в ноябре 2003 г. найдено также, что для R с < 6 ГВ широтные зависимости, полученные с использованием модели Тs01, сильно отличаются от зависимостей, полученных с использованием данных нейтронных мониторов. Можно заключить, что модель Тs01, которая специально была разработана для возмущенных состояний магнитосферы, тем не менее не может отразить в полной мере пространственную конфигурацию возмущенной магнитосферы во время супербурь и, в частности, во время исследуемой бури.

Этот вывод согласуется с результатами работы [Kudela, Bucik, 2005] , в которой сравнивались жесткости обрезания, вычисленные траекторным методом при помощи различных магнитосферных моделей во время нескольких бурь, в том числе 7–8 ноября 2004 г., с результатами наблюдений на нейтронных мониторах и космическом аппарате CORONAS-F. Авторы этой работы утверждают, что для интенсивных бурь результаты для средних широт, полученные с использованием модели Тs01, могут значительно отличаться от наблюдений.

Наш результат, состоящий в том, что B y -компонента ММП играет важную роль в широтном распределении Δ R , а также во взаимосвязи геомагнитной активности с компонентами ММП во время исследуемой бури, особенно на ее восстановительной фазе, заслуживает более подробного рассмотрения.

Связь индексов геомагнитной активности с параметрами межпланетной среды исследовалась в многочисленных работах, в том числе и для периодов магнитных бурь [Dungey, 1961; Burton et al., 1975; Russell, 2000; Newel et al., 2007; Borovsky, 2014; Borovsky, Birn, 2014; и ссылки в них]. Было установлено, что одним из самых геоэффективных параметров ММП является его южная компонента B_z <0, рост которой вызывает пере-соединение магнитного поля солнечного ветра и поля магнитосферы. Однако в работах [Daglis et al., 1999; Gosling et al., 1985; Crooker, 2000; Park et al., 2006; Rawat et al., 2007] было найдено, что B y -компонента при определенных условиях в магнитосфере также может оказывать значительное влияние на пересоеди-нение. В частности, в работе [Rawat et al., 2007] найдено, что B y -компонента ММП играет существенную роль в развитии интенсивной бури в присутствии южной компоненты B_z . Конфигурация ММП, при которой B_y > 0 и B_z < 0, является наиболее геоэф-фективной. Для исследуемой бури отрицательные значения B_z < 0 наблюдались практически на всем протяжении главной и восстановительной фаз начиная с 21:00 UT 7 ноября, но положительная B y > 0 в течение продолжительного времени (больше 18 ч) фиксировалась лишь на восстановительной фазе.

Тот факт, что полученные широтные зависимости Δ R сгс от геомагнитных индексов Dst и K p находятся в противофазе, объясняется, по-видимому, тем, что эти зональные индексы определяются различным образом и отражают поведение различных токовых систем. Dst определяется по вариациям наземного магнитного поля на низкоширотных станциях (18°–35°) и отражает эффект экваториального кольцевого тока. Кроме того, в Dst также вносят вклад частичный кольцевой ток [Liemohn et al., 2001] , поперечные токи хвоста [DuByagin et al., 2014; Ohtani et al., 2001; Turner et al., 2000] и токи на магнитопаузе [Burton et al., 1975; Siscoe et al., 2005] . Dst не описывает динамику частиц радиационных поясов [Reeves et al., 2003] , в то время как K p , напротив, с ней тесно связан [Borovsky, Shprits, 2017] . K _p определяется по субавроральным станциям (44°–62°). Из-за зависимости этого индекса от ширины области авроральных токов (например, [Feldshtein, Starkov, 1962] ) K _p может служить мерой магнитосферной конвекции [Thomsen, 2004] . Во время сильного магнитного возмущения, когда авроральный овал смещается к югу, станции, входящие в сеть K p , начинают фиксировать эффекты магнитосферных токов, текущих в области высоких широт. Эти токи контролируются вертикальной компонентой B z [Potemra, 1987] . Таким образом, можно предположить, что на восстановительной фазе бури 7–8 ноября 2004 г. вариации жесткости обрезания Δ R _сгс регулировались распадом как кольцевого тока, так и высокоширотных токовых систем, при этом влияние последних было более значительным.

ВЫВОДЫ

Мы рассмотрели широтные особенности изменений модельных и наблюдательных геомагнитных порогов на трех фазах бури 7–8 ноября 2004 г.: предварительной, главной и восстановительной. Получены следующие результаты.

• 1.    Во время главной и восстановительной фаз широтная кривая Δ R сгс ( R с ) принимает классическую форму с максимумом падения жесткости обрезания на среднеширотных станциях ( R c ≈ 3 ГВ). На восстановительной фазе максимум двигается к R c ≈ 6÷7 ГВ, т. е. к более низким широтам. Широтное распределение модельных Δ R эф существенно отличается от распределения наблюдательных Δ R _сгс, особенно для средних и низких широт.

• 2.    Наши результаты свидетельствуют о том, что для магнитной бури 7–8 ноября 2004 г. модель магнитосферы Тs01 недостаточно адекватно отражает пространственную конфигурацию возмущенной магнитосферы, причем расхождение отличается на разных фазах бури.

• 3.    На главной и восстановительной фазах бури широтная зависимость Δ R сгс от Dst находится в антифазе с широтной зависимостью Δ R сгс от B y ; широтная зависимость Δ R _сгс от K _p меняется в антифазе с широтной зависимостью Δ R _сгс от B_z . Эти широтные эффекты наиболее четко проявляются на фазе восстановления.

• 4.    На фазе восстановления корреляция Dst с B y выше, чем с B z , а корреляция K p с B y , наоборот, ниже, чем с B z .

Наши результаты свидетельствуют о том, что во время магнитной бури 7–8 ноября 2004 г. преимущественный вклад в развитие токовых систем, определяющих эволюцию Dst на восстановительной фазе бури, вносит не B z -компонента, а B y . Индекс K p , напротив, в большей степени зависит от B_z -компоненты. Связь вариаций жесткости обрезания Δ R сгс с Dst - и K p и их связь с компонентами ММП B_y и B_z обусловлены относительным вкладом различных токовых систем. Наши результаты позволяют заключить, что во время бури, особенно на ее восстановительной фазе, наблюдательные Δ R сгс отражали эффекты как кольцевого тока, так и высокоширотных токовых систем, при этом вклад последних был более значительным.

Работа частично выполнена в рамках базового финансирования Программы фундаментальных научных исследований II.16. Использовалось оборудование Центра коллективного пользования «Ангара» [] и научной установки «Российская национальная наземная сеть станций космических лучей (Сеть СКЛ)».