Возрастная зависимость онкозаболеваемости как следствие гипотезы Конгейма и медленного случайного процесса роста опухолей

Современная теория онкогенеза основывается на гипотезе о том, что нормальная стволовая клетка (НСК), накопив k мутаций в ДНК, становится раковой стволовой клеткой (РСК). Из РСК впоследствии и развивается опухоль [14]. Со времени опубликования работы [4] эта гипотеза является преобладающей. Мутационная гипотеза опиралась на тот факт, что показатели заболеваемости X для целого ряда локализаций зависят от возраста t степенным образом ( X ~ t k^-1 ), а число накопленных мутаций k =6-7. Современные модели онкогенеза [8, 9] также основываются на мутационной гипотезе и учитывают количество мутаций в РСК, рассматриваются стадии развития опухоли, процесс роста опухоли, вероятность диагностирования опухоли.

В работе [8] признано, что зависимость X (t) отличается от степенной. Следовательно, зависимость X (t) не связана с числом мутаций и не является подтверждением мутационной гипотезы. Тогда единственным фактом в пользу мутационной гипотезы является наличие у всех раковых клеток определенных нарушений в геноме [2]. К недостаткам вышеперечисленных моделей канцерогенеза можно отнести то, что они объясняют зависимость X (t) только для нескольких нозологий рака. Для таких заболеваний, как саркома Капоши и Юинга, опухоли щитовидной и молочной желез, шейки матки и ряда других, зависимость X (t) не находит объяснения в рамках мутационной гипотезы. Кроме того, если РСК есть результат мутации НСК, то частота возникновения РСК должна быть пропорциональна числу клеток (массе) органа. Однако, например, предстательная и щитовидная железы близки по массе, а заболеваемость этих желез существенно различается. Пожизненное число заболеваний раком простаты в Австралии в 100 раз больше пожизненного числа заболеваний раком щитовидной железы. Легкие по массе в 50 раз больше предстательной железы, а, например, в Швеции пожизненное число заболеваний раком простаты приблизительно в 4 раза больше такового для рака легких.

Кайдалов О . В . – ведущий научный сотрудник, к.ф.-м.н. МРНЦ РАМН.

В данной работе представлена модель онкогенеза, основанная на гипотезе Конгейма (J.Cohnheim, 1875), впоследствии дополненной Риппертом (V.Rippert, 1911) и Роттером (W.Rotter, 1921) [6, 14]. Согласно гипотезе Конгейма, раковые опухоли происходят из эмбриональных клеток, оставшихся лишними в процессе эмбрионального развития. Роттер высказал предположение о том, что примитивные зародышевые клетки «поселяются» в других органах в процессе развития организма. Предположение Роттера подтверждается повышенной способностью эмбриональных клеток к миграции [2]. Как полагал Рипперт, измененная окружающая среда позволяет эмбриональным клеткам ускользать от контроля со стороны организма над их размножением. Результаты работ [10, 15] подтверждают это предположение.

Представляется маловероятным, чтобы на стадии эмбрионального развития оставалось несколько «лишних» эмбриональных клеток, в потенциале содержащих план или программу построения органов. Возможно, что в период раннего эмбриогенеза на каком-то этапе природа не может обойтись без образования «лишней» клетки. Поэтому дополним гипотезу Конгейма предположением, что на фазе эмбрионального развития остается одна «лишняя» эмбриональная клетка Конгейма (ЭКК). Следствие гипотезы Конгейма : в отсутствии других причин смерти у всех людей будет зарегистрирована опухоль. Это совпадает с мнением [3]: «…большинство живущих на земле должны умирать от рака, но не каждый до него доживает».

Далее, по Роттеру, ЭКК с какой-то вероятностью может оказаться в любом органе развивающегося плода. Следствие предположения Роттера : различие между популяциями в заболевании органов связано с вероятностью миграции ЭКК в данный орган.

Согласно предположению Рипперта, ЭКК, являясь «лишней», начинает неконтролируемое организмом самостоятельное существование, что приводит к развитию опухоли. Следствие предположения Рипперта : неконтролируемое развитие опухоли происходит в условиях дефицита питательных веществ и рост опухоли можно рассматривать, до определенного момента, как медленный случайный процесс.

Материалы и методы

Данные по онкозаболеваемости и их предварительный анализ. Для сопоставления результатов теоретических расчетов с фактическими данными по онкозаболеваемости использовались данные [5]. Данные по онкозаболеваемости по 30 регистрам из [5] объединены в один регистр (далее Р30, 1,34·10⁹ человеко-лет, 5,69·10⁶ случаев). В таблице 1 приведен список этих регистров с указанием суммарного числа случаев заболеваний и пожизненного числа заболеваний F С . Выбранные регистры содержат данные для 18 возрастных интервалов. Данные о заболеваемости за 5-летние возрастные интервалы при сопоставлении с теорией отнесены к возрастам t i =2,5+5·( i -1), i =1,2, …, 18.

Таблица 1

Сведения по регистрам, данные которых использовались в работе

Регистр	Случаев, тыс.	F С , % (муж.)	F С , % (жен.)
Р30	5690	55,3	40,2
UK, ENGLAND (1993-1997)	1234	57,2	43,0
CANADA (1993-1997)	602	56,0	41,6
USA, SEER: WHITE (1993-1997)	461	57,4	44,2
THE NETHERLANDS (1993-1997)	333	56,7	39,3
ITALY (1993-1997)	295	60,3	43,0
CZECH REPUBLIC (1993-1997)	262	60,9	46,3
AUSTRALIA (1993-1997)	317	58,8	41,5
SWEDEN (1993-1997)	205	50,1	38,9
DENMARK (1993-1997)	144	55,7	47,3
SPAIN (1992-1995)	139	53,4	34,5
FINLAND (1993-1997)	122	58,6	44,5
FRANCE (1993-1997)	142	57,1	37,1
NORWAY (1993-1997)	99	53,7	39,9
SLOVAKIA (1993-1997)	98	53,9	38,0
SWITZERLAND(1993-1997)	94	59,1	44,2
GERMANY, SAARLAND (1993-1997)	32	59,8	44,6
IRELAND (1994-1997)	72	65,0	51,3
ICELAND (1993-1997)	5	55,5	45,1
BELGIUM, LIMBURG (1997-1998)	8	63,5	45,2
BELGIUM, FLANDERS, (EXCL. LIMBURG)	48	53,6	37,8
AUSTRIA, TYROL (1993-1997)	14	59,5	43,1
AUSTRIA, VORARLBERG (1993-1997)	7	59,6	45,1
YUGOSLAVIA, VOJVODINA (1993-1997)	37	42,9	32,4
CROATIA (1993-1997)	79	47,9	31,6
POLAND, LOWER SILESIA (1993-1997)	48	51,3	34,9
POLAND, WARSAW CITY (1993-1997)	32	48,3	36,9
POLAND, KIELCE (1993-1996)	13	43,9	29,5
CHINA (1993-1997)	332	39,2	29,7
JAPAN (1993-1997)	294	52,6	31,9
KOREA (1993-1997)	108	49,5	28,9

По аналогии с [1], случай заболевания будем рассматривать как отказ, а заболеваемость в популяции характеризовать частотой отказов (частота заболеваний). Данные по онкозаболеваемости далее представляются, за небольшим исключением, в виде частоты заболеваний N F ⁱ (t) , где i – нозология (МКБ-10) или морфология опухоли. В предположении, что иных причин отказов кроме онкозаболеваний нет, частота заболевания связана с показателем общей заболеваемости Л⁰ известным образом:

t

- J 2 0 d т

NfW = i(t)• e0   , i = X<

где Л - показатель заболеваемости для i -й нозологии, i =0 - общая онкозаболеваемость. Кумулятивное число всех заболеваний к возрасту t есть

t

F0(t) = XJ NFd т = X FVt).

Как следствие гипотезы Конгейма, пожизненное число заболеваний F C = F 0 (^м)=1 или 100 %. Согласно Роттеру, локализация ЭКК (в последствие локализация опухоли) событие случайное, тогда

W

P i = J N ^ ( т )d т                                            (3)

есть вероятность миграции ЭКК в данный орган. Поскольку нет оснований отвергать другие причины возникновения рака [2, 14], то F С > 1.

На рисунках 1, 2 приведены зависимости n F (t) и a°(t) (мужчины, все виды рака) для каждого регистра (серый цвет) и Р30 (черный цвет). Шкала возраста дополнена шкалой года рождения заболевших. Отметим, что практически для всех регистров зависимость n F (t) близка к гауссовой. Максимум частоты заболеваний n F наблюдается при t₀ ~ 70-80 лет. Значение F С (табл. 1, Р30) составляет для мужчин 55 %, что существенно меньше 100 %. Однако из рисунка 1 видно, что если продолжить кривую частоты отказов на возраст более 90 лет, то недостающие 45 % заболеваний придутся на этот возрастной интервал.

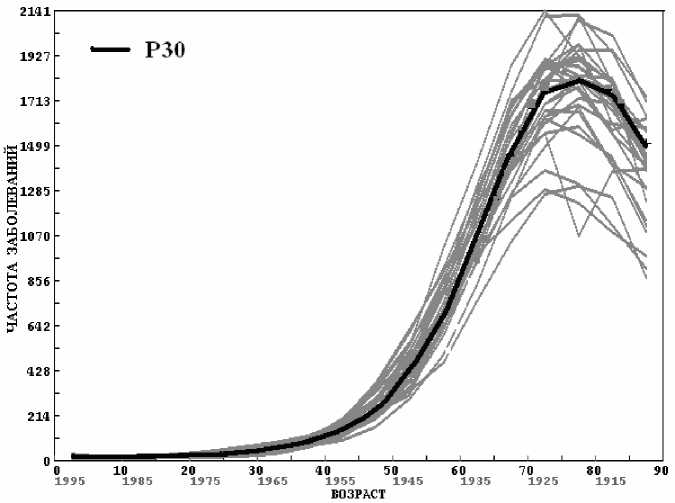
Рис. 1. Зависимость частоты заболеваний всеми видами рака (мужчины) для каждого регистра (серый цвет) и Р30 (черный цвет). Приведена шкала года рождения заболевших в данном возрасте.

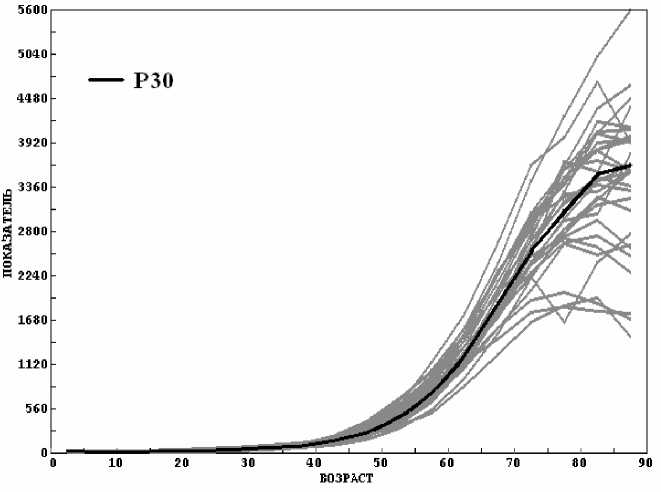
Рис. 2. Зависимость показателей заболеваемости всеми видами рака (мужчины) для каждого регистра (серый цвет) и Р30 (черный цвет).

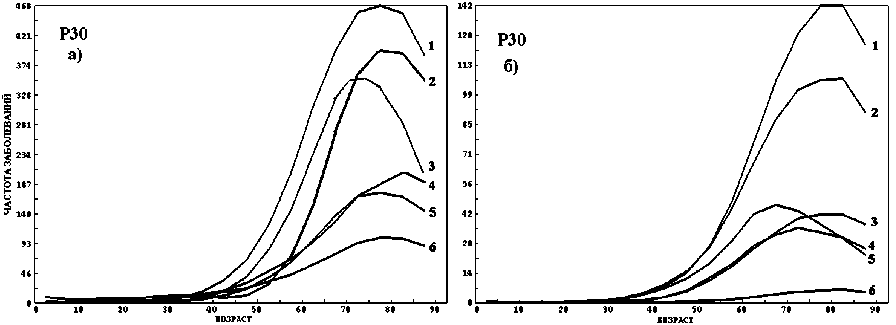
Рис. 3. Зависимость N F (t) для основных нозологий (а): 1 – органы пищеварения (С15-26), 2 – половые органы (С60-63), 3 – органы дыхания (С30-39), 4 – кожа (С43-44), 5 – мочевые пути (С64-68), 6 – лимфоидные ткани (С81-96); для нозологий органов пищеварения (б): 1 – толстый кишечник (С18), 2 – желудок (С16), 3 – поджелудочная железа (С25), 4 – пищевод (С15), 5 – печень (С22), 6 – желчный пузырь (С23).

Аналогичная зависимость N p (t) наблюдается для большинства нозологий и морфологий опухолей. На рисунке 3 представлена зависимость N p (t) (мужчины, Р30) для основных нозологий (а) и 6-ти нозологий органов пищеварения (б). Как и на рисунке 1, зависимости близки к гауссовой.

Рост опухоли как случайный процесс. Как в органах человека, так и в опухолях соотношение стволовых и обычных клеток оценивается как 10-2-10-4 [6, 14] и, следовательно, РСК строят опухоль, также как НСК строят ткань органа. Различие состоит в том, что фактор, кон- тролирующий симметричное деление РСК, в опухоли отсутствует, а асимметричное деление происходит как и в нормальном органе. НСК находится в окружении специальных клеток или нише – своего рода инкубатор для производства клеток [7, 13]. Ниша обеспечивает постоянный приток веществ, необходимых для производства новых клеток, защиту от внешних неблагоприятных воздействий и контролирует доставку сигналов НСК. (Можно предположить, что именно повреждение ниши в эксперименте Роуса (Rous Р., 1941) [14] приводило к развитию рака.) Каждая НСК содержит в потенциале огромное число клеток и, следовательно, не должна воспринимать сигналы к апоптозу [11]. Следовательно, РСК также должны обладать этим свойством. Данных о существовании ниши у РСК нет, что может быть причиной, по которой опухоль представляет «карикатуру» на орган [12]. Предположительно [7], РСК могут использовать ниши НСК при инвазии и метастазировании. Также РСК могут улавливать сигнальные молекулы, предназначенные для НСК. Этот процесс носит случайный характер (диффузия сигнальных молекул) и может ускорять рост опухоли. Не имея ниши, РСК, как и обычные клетки опухоли, находятся в условиях дефицита питательных веществ и рост опухоли можно рассматривать как медленный случайный процесс [2, раздел 17.3.7].

Основные закономерности возрастной зависимости частоты заболеваний всеми видами рака, приведенной на рисунке 1, могут быть объяснены простейшей моделью роста опухоли. Свяжем факт заболевания с возрастом t , когда количество клеток в опухоли достигнет некоторого критического значения x m , и проследим за заболеваемостью в когорте из N человек с возраста t =0 и далее. Согласно гипотезе Конгейма, у каждого человека при t =0 есть ЭКК. Если прирост клеток опухоли происходит с детерминированной скоростью v , не зависящей от индивидуальных особенностей человека, то частота заболеваний будет иметь вид:

~          V         vtNF (t) = N — 5 ( m ) xm xm

– все N человек в когорте заболевают одновременно в возрасте t₀ = x_m / v . Согласно рисунку 1, максимум частоты заболеваний наблюдается в возрасте t 0 ≈ 80 лет. Принимая x m =10⁹ клеток [2, 16] (при размере клетки 10 мкм объем опухоли составит 1 см³), находим, что скорость роста опухоли v ≈ 10⁷ клеток/год (далее кл/г). Для сравнения, за 9 месяцев плод человека достигает веса 3,5 кг и состоит примерно из 3,5·10¹² клеток. Скорость роста плода составляет 4·10¹² кл/г. Таким образом, темпы роста опухоли по предварительной оценке очень низкие.

Предположим, что скорость роста опухоли случайная величина, и представим ее в следующем виде:

v = П = V(n,t) + u(n,t),                                       (5)

где n(t) – численность клеток опухоли в момент времени t, V – детерминированная скорость, обусловленная увеличением числа РСК, а и - случайная дельта-коррелированная функция с u(n,t) = 0 (отмирание и рождение обычных клеток опухоли). Таким образом, у части людей из когорты опухоль достигает критического размера раньше, у части – позже. Различие в скоро- стях роста опухолей приведет к расплыванию дельта-функции (4) и частоту заболеваний можно приближенно записать в виде:

~

NF(t)~Cexp

I

^(xm - ^vt) 2 '

~ lnNF ~ lnC

(t 0 - t) ² B/v²

Следствием гипотезы Конгейма и предполагаемой зависимости (6) является то, что онкологическая заболеваемость не «растет» со временем, а «молодеет» – t 0 уменьшается и максимум частоты заболеваний смещается в сторону младшего возраста. Это можно объяснить увеличением скорости v (например, ухудшение экологических условий).

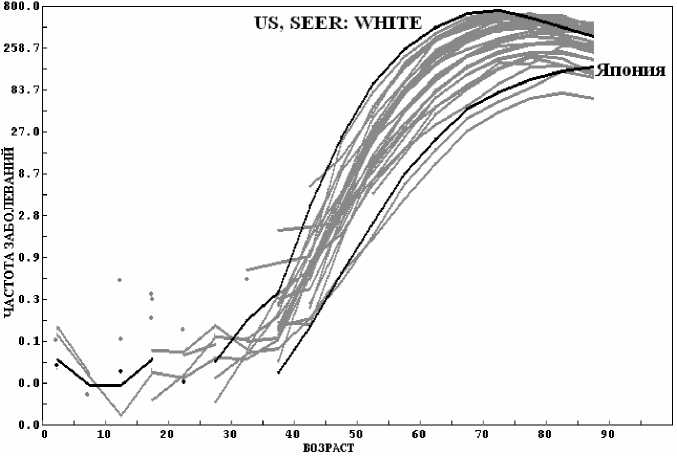
Рис. 5. Зависимости частоты заболеваний раком простаты (С61, мужчины) от возраста для 30 регистров.

Аналогичный пример, приведенный на рисунке 6, дают регистры Швеции (SWEDEN, F С =50 %) и Польши (POLAND, LOWER SILESIA, F С =51 %). В Швеции для рака легких и простаты F C34 =3,8 % и F C61 =14,6 %, разница – 10,8 %. В Польше F C34 =14,3 % и F C61 =4,3 %, соответственно, а разница – 11 %. Таких примеров, подтверждающих предположение Роттера, достаточно много.

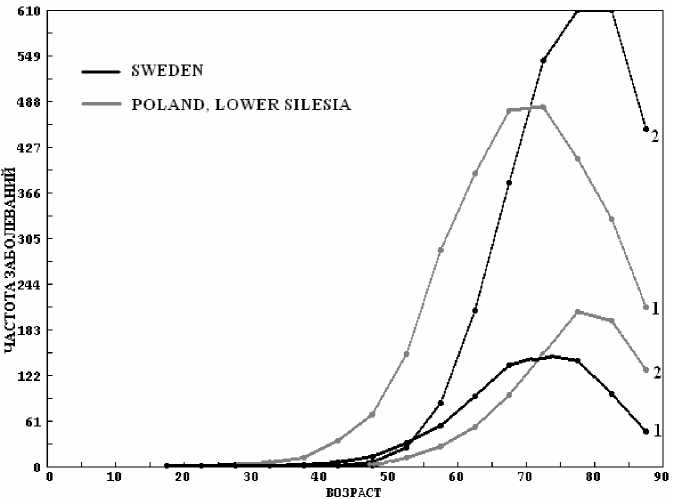
Рис. 6. Частота заболеваемости раком легких (1) и простаты (2) по данным регистров SWEDEN и POLAND, LOWER SILESIA.

Общая закономерность в частоте заболеваний. Предварительный анализ и интерпретация данных по онкозаболеваемости показывает, что гипотеза Конгейма и модель случайного роста опухоли объясняет характерные особенности зависимости N F (t) . Частота заболеваний существенно варьирует от нозологии к нозологии, от регистра к регистру. Для выявления общей закономерности в частотах заболеваний приведем N'_F(t) к одному масштабу, а именно, рассмотрим нормированную частоту:

n i (t) = -*И-.

max[NF(t)]

На рисунке 7 приведена зависимость n F (t) для восьми типов опухолей. Как видно из рисунка, все зависимости n F (t) , подобны зависимости (6), смещенной вправо или влево по оси возраста (различные параметры x_m , v и B ). Из зависимостей n F (t) для медулобластомы и ретинобластомы следует, что рост опухоли может начинаться в период внутриутробного развития и приводить к гибели плода. Что, впрочем, является известным фактом.

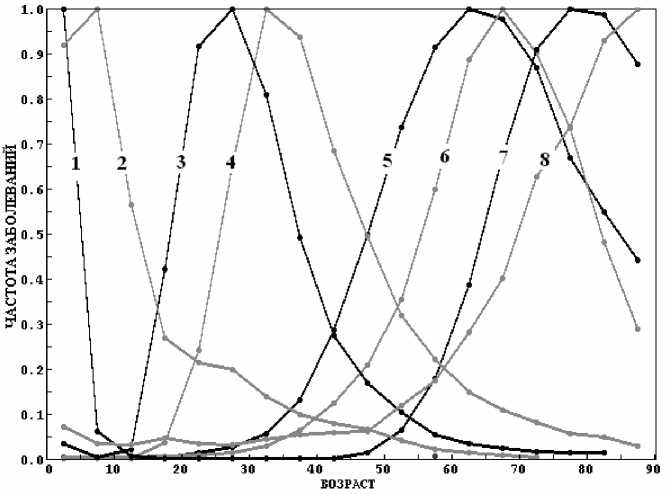
Рис. 7. Зависимость n F (t) для восьми типов опухолей: 1 - ретинобластома,

2 – медулобластома, 3 – тератома, 4 – семинома, 5 – рак языка (С01-02), 6 – гепатоцеллюлярная карцинома, 7 – рак простаты (С61), 8 – лейкемия (С95.0).

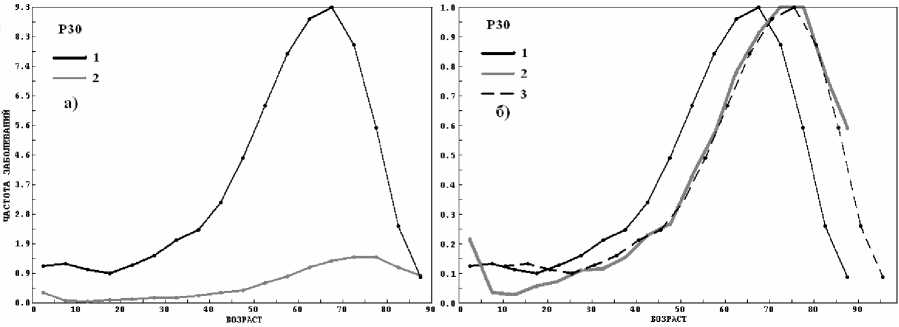
Рис. 8. Зависимость фактической N F (t) (а) и нормированной частоты заболеваний n ^ ft) (б)

для опухолей: 1 – астроцитома (С70-72), 2 – перитонеум, ретроперитонеум (С48), 3 – то же, что и 1, но смещенная вправо на 8 лет.

На рисунке 8 (а,б) показаны N'_F(t) и n_F(t) для двух морфологий опухолей. На рисунке 8а трудно найти что-либо общее в частотах заболеваний. Однако в нормированном виде (рис. 8б) зависимости n_F(t) практически совпадают, если при этом сместить зависимость n_F(t) для астроцитомы на 8 лет вправо.

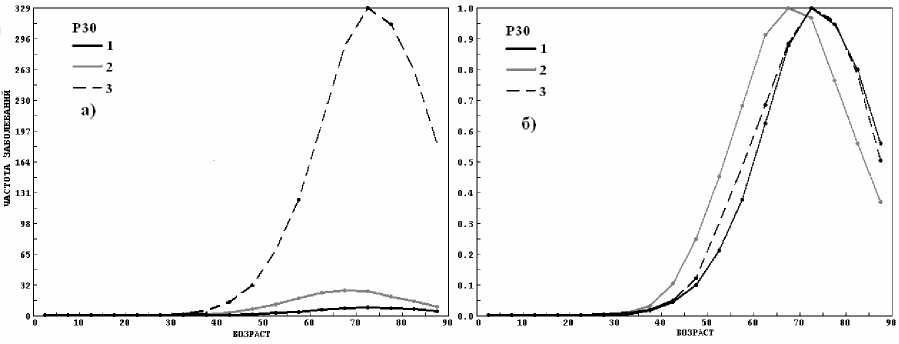
Рис. 9. Зависимость фактической N'_F(t) (а) и нормированной частоты заболеваний n_F(t) (б) для нозологий опухоли: 1 – мезотелиома (С45), 2 – гортань (С32), 3 – легкие (С34).

На рисунке 9 показано то же, что и на рисунке 8, но для других нозологий. Таким образом, в нормированном виде зависимости n_F(t) имеют большое сходство, что говорит о единой природе развития опухолей.

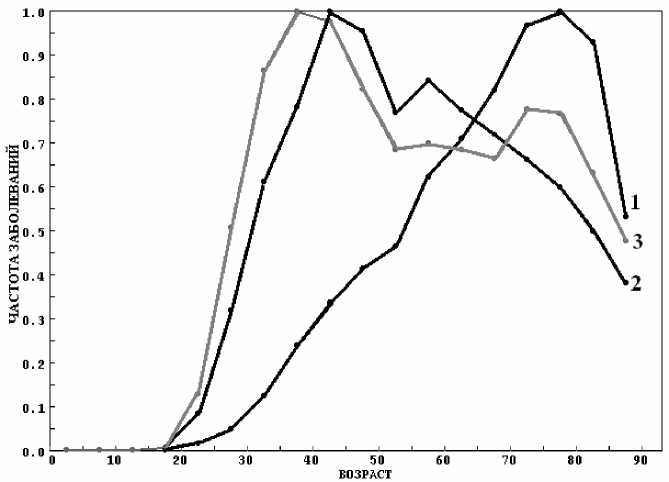
Рис. 10. Зависимость n_F ⁵³ (t) для рака шейки матки (С53) для регистров:

1 – CHINA, 2 – CZECH. REPUBLIC, 3 – UK, ENGLAND.

Анализ данных заболеваемости по некоторым локализациям позволяет сделать вывод о том, что NF(t) может быть суммой нескольких зависимостей вида (6). На рисунке 10 показаны зависимости nFi (t) для рака шейки матки (С53) для трех регистров. Эти зависимости можно интерпретировать следующим образом. Заболеваемость складывается из двух мод (6) с различными параметрами C, B и v:

г n5FF (t) ~ c1exp

I

s-v 1

B i V J

г

+C2exp

I

(tzt02)2 ) B2/v2 ,

Таким образом, часть женщин (~ с 1 ) из популяции заболевает в возрасте 20-60 лет ( t 01 ~ 35-40 лет), а часть (~ с 2 ) – в пожилом возрасте ( t 02 ~ 75-80 лет). Согласно рисунку 10, в Чехии – с 1 > с 2 , в Китае – с 1 <с 2 , в Англии – с 1 ~ с 2 .

Уравнение изменения численности когорты вследствие онкозаболеваемости. Рас- смотрим уравнение (5) для простейшего случая: V=const и v=v(t). Уравнению (5) можно сопос- тавить уравнение Фокера-Планка:

д N д t

^^^е

u

д N

д x

+ D

д 2 N д X2

со следующими начальными и граничными условиями

N(x,0) = Q(x) ,

J(0,t) = -DЦ^Х=o + и• N(0,t) = 0 , d X

N(Xm,t) = 0 ,                                                    (11)

0 < X < Xm, t > 0, где N(x,t) - плотность распределения когорты по размерам опухоли, и - детерминированная скорость роста опухолей, D - коэффициент диффузии. Начальное условие (9) - у части людей опухоль может развиваться в период внутриутробного развития, Q(x) есть плотность распреде xm

N 0 = / Q(x) • dx , где

ления когорты по размерам опухоли на момент рождения t =0, причем

N₀ - численность когорты при t =0. Условие (10) - РСК не гибнут, условие (11) - нет людей, у которых х > x_m (заболевший выбывает из когорты).

Количество человек M(t) , у которых х < x_m (здоровые) есть:

m

M(t) = / N(x,t)dx .

Интегрируя (8) от 0 до x_m , с учетом граничных условий, имеем:

d M = D д N(x,t) д t д x

Откуда частота заболеваний и показатель заболеваемости в случае общей заболеваемо- сти есть:

NF(t) =-Dд N(x,t)L_x , X(t) = NF^t)

F() dx lx= xm,        M(t) ■

Далее N_F будем называть решением уравнения (8). Для i -й локализации опухоли ( i =1,2,...) зависимость N_Fi(t) , кроме параметров x_mi , u i , D i , характеризуется еще и пожизненной вероятностью заболевания p i (вероятность, что ЭКК имеет i -ю локализацию). Общая заболеваемость ( i =0) представляется в виде суммы:

Nf0 (t) = 2 Pi • Nf (t, xmi, Ui, Di ) = 2 Nfi (t)

P0 = 2 Pit = 1

Определение A (t) (14) получено для общей заболеваемости: i =0, р 0 =1. При переходе к локализациям опухоли для определения показателя заболеваемости A , (t) необходимо знать A o (t) . Фактическое значение р , определить по данным о заболеваемости затруднительно, поскольку данные о заболеваемости в возрасте более 85 лет объединены в одну возрастную группу. Поэтому теоретически рассчитанная нормированная частота n_Fi(t) умножалась на постоянную С _; , подбираемую из условия наилучшего совпадения с фактической частотой заболевания.

Приведем уравнения к безразмерному виду путем замены:

x = ХтУ, t = -mт, u = UUd, N = N/No, где ud= D/xm - диффузионная скорость роста опухоли. В результате уравнение (8) примет вид:

∂N     ∂N ∂2N= -U +

∂τ      ∂ y ∂ y2

Решение (17) N(y, T ) , как и N F ( T ) , зависят только от одного параметра - безразмерной скорости U .

Приближенное аналитическое решение и его интерпретация. В случае U>>1 и Q(У)=23(У) - все люди на момент рождения имеют опухоль из 1 ЭКК, решение (17) на бесконеч ном интервале -^ < у < ^ имеет вид:

(y - U τ ) ²

-