Вращающиеся элегантные пучки Бесселя-Гаусса

В 1987 году Гори [1] рассмотрел пучки Бесселя-Гаусса (БГ-пучки). Комплексная амплитуда таких пучков описывается произведением Гауссовой функции на функцию Бесселя первого рода n-го порядка и на фазовую функцию, описывающую угловую гармонику. Комплексная амплитуда БГ-пучка удовлетворяет параксиальному уравнению распространения. Эти пучки имеют радиально-симметричное распределение интенсивности и обладают орбитальным угловым моментом (ОУМ). Радиальная симметрия сохраняется при распространении пучка. Но БГ-пучки не являются модами свободного пространства, так как при распространении не только масштабно изменяются, но также перераспределяется световая энергия между различными кольцами в распределении интенсивности в поперечном сечении пучка. БГ-пучки обобщались в ряде работ [2-4]. Например, в [4] рассмотрены пучки Гельмгольца-Гаусса, частным случаем которых являются пучки Бесселя-Гаусса [1]. БГ-пучки имеют конечную энергию, но известны также моды Бесселя, не обладающие конечной энергией [5]. Моды Бесселя являются решением уравнения Гельмгольца [6] и при распространении в однородном пространстве сохраняют свою интенсивность, поэтому также называются бездифракционными пучками Бесселя [5]. Линейная комбинация мод Бесселя с произвольными коэффициентами также является решением уравнения Гельмгольца. В [7] предложен алгоритм расчёта фазового оптического элемента, который формирует бездифракционные пучки Бесселя с заданным модовым составом. В [8] предложено рассматривать пучок Матье как альтернативу пучку Бесселя. В [9] показано, что линейная комбинация чётного и нечётного пучков Матье с комплексными коэффициентами обладает ОУМ. Но сами пучки Матье не обладают ОУМ. Интересно [10], что линейная комбинация двух мод Эрмита-Гаусса с комплексными коэффициентами, которые не обладают ОУМ, обладает ОУМ. Периодические функции Матье можно разложить в ряд Фурье [6]. Например, чётные функции Матье раскладываются по косинусам от полярного угла в цилиндрической системе координат, а нечётные - по синусам. Поэтому безди-фракционный пучок Матье можно представить как линейную комбинацию мод Бесселя. Такие пучки рассматривались в [11].

Интересно найти линейные комбинации БГ-пуч-ков, которые описывались бы простыми аналитическими функциями, с помощью которых можно аналитически рассчитать некоторые свойства таких пучков. В данной работе рассматривается линейная комбинация БГ-пучков, которая описывается функцией Бесселя с комплексным аргументом. По аналогии с элегантными пучками Эрмита-Гаусса и Лагерра-Гаусса, комплексная амплитуда которых пропорциональна соответственно полиномам Эрмита и Лагерра от комплексного аргумента, рассматриваемые пучки были названы элегантными пучками Бесселя-Гаусса. Пока- зано, что такой асимметричный пучок Бесселя– Гаусса (аБГ-пучок) имеет в начальной плоскости счётное число изолированных нулей интенсивности, расположенных на горизонтальной оси. Все эти нули (кроме осевого) порождают оптические вихри с единичным топологическим зарядом и противоположными знаками с разных сторон от начала координат. Нуль интенсивности на оптической оси порождает оптический вихрь с топологическим зарядом n. При распространении в свободном пространстве аБГ-пучки вращаются вокруг оптической оси. Показано, что такие пучки имеют ОУМ, который растёт с номером n, а также увеличивается с ростом параметра c асимметрии пучка. Причём ОУМ аБГ-пучков может быть как целым, так и дробным.

1. Линейная комбинация БГ-пучков

Запишем комплексную амплитуду БГ-пучка [1] в начальной плоскости z =0:

I r 2       )

E„ (r,ф,z = 0) = expl--2 + inф IJ (ar),

I ® 0       J

где α = k sin θ 0 = (2 π / λ )sin θ 0 – масштабирующий множитель, ω 0 – радиус перетяжки Гауссова пучка, k = 2π/λ – волновое число света с длиной волны λ, θ₀ – угол конической волны, формирующей пучок Бесселя. В любой другой плоскости z комплексная амплитуда (1) будет иметь вид:

I г a z I

E „ ( r , Ф , z ) = q ( z ) exp l ikz - Ix (      2 kq ( z ) J

I r x exp|--: , J inф I J ( too q (z)       J

a r

q ( z ) :

где q(z) = 1 + iz/z0, z0 = kto0/2 - длина Рэлея, Jn(x) - функция Бесселя первого рода n-го порядка. Пучки (2) не являются параксиальными модами свободного пространства, так как аргумент функции Бесселя комплексный. Рассмотрим следующую суперпозицию БГ-пучков q = q(z):

„ ₍ a -i I         i a z     r ² ।

E_n ( r , ф , z ; c ) = q exp | ikz - —---- Ix

(      2 kq   q to ₀ J

^

Z p = 0

c p exp ( in ф + ip ф )

a r

p !

n + p

.

q

Поле (3) формирует параксиальный асимметричный пучок Бесселя–Гаусса (аБГ-пучок) при любых целых n и любой комплексной постоянной с . Но для простоты в дальнейшем будем считать постоянную c вещественной положительной величиной: c ≥ 0. Хотя если рассмотреть c как комплексную величину c = | c | arg c или учесть, что она может быть отрицательной c <0, то распределение интенсивности поля (3) повернётся на угол arg c вокруг оптической оси. При c =0 в (3) отличным от нуля остаётся только одно слагаемое при p =0, и аБГ-пучок становится обычным БГ-пучком (1), (2).

Здесь рассматривается линейная комбинация БГ-пучков в виде (3) потому, что этот ряд равен функции Бесселя с комплексным аргументом. Действительно, в [12] есть справочный ряд (выражение 5.7.6.1):

^ ,k

Z ^Jk + V ( x ) = k=0 k!

= x ' ² ( x - 2 t ) ^{- V /2} J_V (V x ² - 2 tx ) .

С помощью (4) преобразуем (3) и получим:

E_n ( r , ф , z ; c ) = — exp | ikz q I

i a ² z

2 kq

r 2 . ■

--+ in ф I x q to 0        J

ar ar - 2 cq exp (i ф)

x J_n { q ¹ ^a r |^ a r - 2 cq exp ( i ф ) ] } .

Выражение (5) является замкнутой формой комплексной амплитуды трёхпараметрического мейства параксиальных скалярных аБГ-пучков.

для се-Два

непрерывных вещественных параметра аБГ-пучков управляют масштабом ( a ) и степенью асимметрии ( с ). Радиус Гауссова пучка ω₀ считается одинаковым для всего семейства аБГ-пучков. Целый параметр n вместе с непрерывным c определяют величину ОУМ. Когда знаменатель в (5) равен нулю, тогда и аргумент функции Бесселя равен нулю. Неопределённость ноль на ноль раскрывается.

Пучок (5) имеет счётное число изолированных нулей интенсивности, которые порождают оптические вихри с единичным топологическим зарядом, кроме осевого нуля, который порождает оптический вихрь с n -м топологическим зарядом. Для получения полярных координат нулей аБГ-пучка приравняем аргумент функции Бесселя в (5) корню функции Бесселя ^Y np ^{( J} n ( Y np ) ⁰⁾ :

a ² r ² - 2 a cqr exp ( i ф ) = Y 2 _pq ².

Выделим вещественную и мнимую части этого уравнения:

I a ² r ² - 2 a c|q|r cos ( ф + Т ) = Y 2 _p |q |2 cos ( 2 T ) ,

|-2ac|q|rsin(ф + Т) = Y2p |q|2 sin(2Т), где Т = arctg(z/z0) - фаза Гоу. Из (7) находятся коор- динаты точек с нулевой интенсивностью:

ф np

= — arccos

,    Y2        , , cos(2Т)-^^pprsin2 (2Т)

rnp = q VY2p cos(2Т) + 2c2 ± 24D, где D = (c2 -Y2p sin2 Т)(c2 +Y2p cos2 Т). Из обоих уравнений (8) следует: чтобы координаты нулей были вещественными, необходимо выполнение условия:

Y np ^{sin T5} c . ⁽⁹⁾

Из (9) следует, что если c >  у _np , то все нули интенсивности с номерами от q =0 до q = p при распростра-

нении не исчезают (так как для этих нулей у nq <  c и неравенство (9) выполняется для любых расстояний z ), однако остальные нули с номерами q = p + 1, p +2, ...

сти, зеркально-симметричное относительно оси x =0 по сравнению с пучком (5), имеет амплитуду вида:

( r2 ^

E_n ( r , ф , z = 0; c ) = exp I--- I x

I °0 J

(для которых c <  у nq ) пропадают на некотором расстоянии z = cz 0 /( y nq ² – c ² ) ^1/2 .

При z =0 вместо (8) запишем:

^гр +

<

r p -

= «■' (c + Vc 2 + Y2p ), фnp = 2 pn.

= “-1 (7c2 + Y2p - c). фnp = (2P +')”.

TO

xZ

p = 0

( - c ) ^p exp [ i ( n + p ) ф ]

( r2

= exPl--2

I «0

p !

ar

J « + p ^{( a r} ) =

_ a r + 2 c exp( i ф ) _

n /2

x

x J_n { J ar [ a r + 2 c exp( i ф ) ] } exp( in ф ).

Из (10) следует, что интенсивность в сечении аБГ-пучка несимметрична относительно начала координат, так как r_p+ >  r_p– . Причём, когда с >0 растёт, асимметрия аБГ-пучка увеличивается, а при c =0 изолированные нули аБГ-пучка пропадают, а появляются кольца нулевой интенсивности радиально-симметричного пучка Бесселя–Гаусса. Все нули аБГ-пучка (кроме осевого при r =0) порождают оптические вихри с единичным топологическим зарядом и противоположными знаками с разных сторон от начала координат. Для нулей интенсивности с радиальными координатами r p+ топологический заряд оптических вихрей +1, для r p- – топологический заряд –1. Чтобы сменить знаки этих оптических вихрей на противоположные, надо вместо (5) взять комплексно сопряжённое выражение. Из (8) видно, что нули интенсивности, а значит, и само распределение интенсивности в поперечной плоскости аБГ-пучка вращаются при распространении. Но вращение это достаточно сложное. Тoлько когда c >> 1, в первом уравнении в (8) можно пренебречь вторым слагаемым в квадратных скобках, и тогда картина интенсивности в поперечном сечении пучка вращается как единое целое. При этом полярный угол меняется с расстоянием z :

ф = arctg z . (11)

I z о)

Из (11) следует, что аБГ-пучок от начальной плоскости z =0 до расстояния Рэлея z = z 0 повернётся против часовой стрелки на π/4, а на остальном участке пути от z = z 0 до z = ∞ – ещё на π/4, и, таким образом, на всём протяжении пути пучок повернётся на π/2. Вращение аБГ-пучка не зависит от номера n , то есть вращаться будет и нулевой пучок при n =0.

На рис. 1 показаны распределение интенсивности и фазы аБГ-пучка (5) при разных значениях параметра асимметрии с. При моделировании были использованы следующие значения параметров: длина волны X = 532 нм, радиус перетяжки Гауссова пучка W0 =10X, масштабирующий множитель a = 1/(10X), границы расчётной области -40X 0 интенсивность из кольцевой становится похожей на полумесяц, выпуклый в правую сторону. Можно записать выражение для аБГ-пучка, имеющего вид полумесяца, выпуклого в левую сторону. аБГ-пучок, имеющий распределение интенсивно- а)

в)

д)

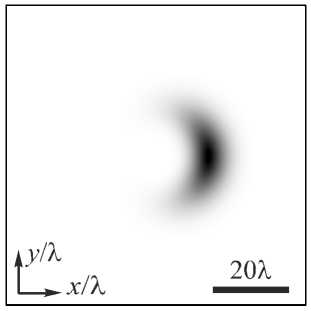
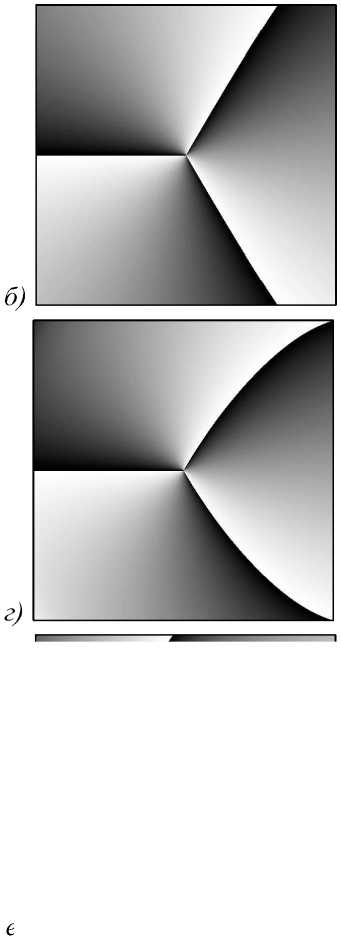
Рис. 1. Распределение интенсивности(негатив) (а, в, д) и фазы (б, г, е) светового пучка (5) третьего порядка (n = 3) в начальной плоскости при z = 0 для разных значений параметра асимметрии с: 0,1 (а, б); 1 (в, г); 10 (д, е)

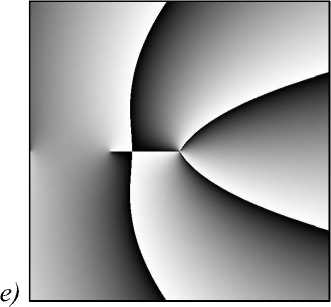
Также на рис. 1 видно, что нули интенсивности, лежащие на оси x <0, с ростом с приближаются к центру координат: на рис. 1 б , г их ещё не видно, а на рис. 1 е появился один ноль. Такое поведение нулей следует из второго уравнения (10) при больших с >> 1. В центре рис. 1 б , г , е расположен нуль интенсивности третьего порядка ( n =3).

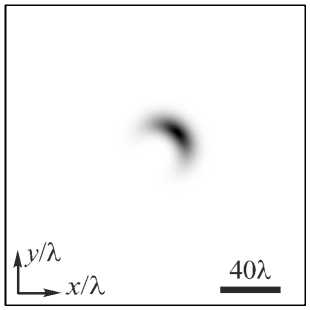
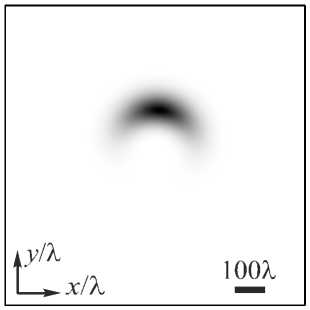
На рис. 2 показаны распределения интенсивности и фазы аБГ-пучка третьего порядка (n = 3) при относительно большом значении параметра с = 10 на разных расстояниях вдоль оптической оси в плоскостях z =0 (а, б), z = z0 (в, г), z = 10z0 (д, е). На рис. 2 видно, что пучок вращается вокруг оптической оси. На расстоянии Рэлея z0 картина интенсивности повернулась против часовой стрелки на 45 градусов (рис. 2в), а на расстоянии 10z0 картина интенсивности повернулась почти на 90 градусов (рис. 2д).

а)

в)

д)

^{г )}

б)

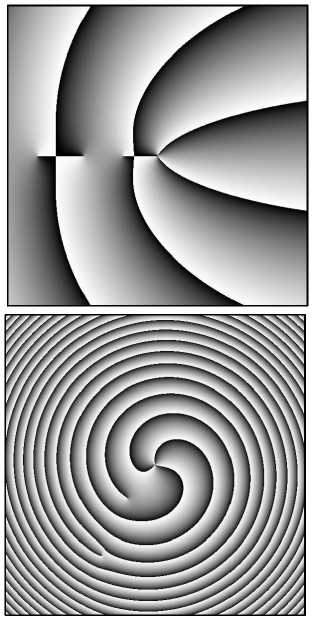
масштабирующий множитель α = 1/(10 λ ), границы расчётной области –300 λ ≤ x , y ≤ 300 λ (рис. 3 а , б ) и – 1000 λ ≤ x , y ≤ 1000 λ (рис. 3 в , г ). При этих параметрах вращение аБГ-пучка уже не описывается простой формулой (11), так как параметр асимметрии c небольшой. На рис. 3 видно, что картина интенсивности поворачивается на расстоянии z = z 0 почти на 90 градусов против часовой стрелки. А изолированные нули интенсивности, которые лежат на оси x и видны на рис. 3 б , при распространении пучка «пропадают»: на рис. 3 г при z = z 0 не видно нулей интенсивности, кроме центрального.

е)

Рис. 2. Распределение интенсивности (негатив)(а, в, д) и фазы (б, г, е) светового пучка (5) третьего порядка (n = 3) на разных расстояниях: z = 0 (а, б), z = z₀ (в, г), z = 10z 0 (д, е)

Размер картинок на рис. 2 разный: –80 λ ≤ x , y ≤ 80 λ ( а , б ); –100 λ ≤ x , y ≤ 100 λ ( в , г ) и –500 λ ≤ x , y ≤ 500 λ ( д , е ). Остальные параметры те же, что и для рис. 1. На рис. 2 также видно, что нули интенсивности, лежащие на оси x при z =0, тоже начинают вращаться против часовой стрелки c увеличением z . На рис. 2 б видны три изолированных нуля интенсивности на оси x слева от центрального нуля 3-го порядка. На рис. 2 г видно, что при z = z ₀ осталось только два нуля, которые повернулись на 45 градусов, а на рис. 2 е ( z = 10 z 0 ) эти два нуля объединились в один ноль 2-го порядка и повернулись почти на 90 градусов.

Из неравенства (9) следует, что, так как γ _{n 1} > 1 для всех целых n , при c ≤ 1 все изолированные нули интенсивности, лежащие на оси x (кроме центрального нуля), будут «пропадать» по мере распространения пучка, начиная с самых дальних нулей (γ p >>1). Последним «пропадёт» первый ноль интенсивности γ₁ при z , равном :

,                 • I c I z = z0 tg arcsin I — I .

I Yi J

Нули интенсивности «пропадают» в том смысле, что значения их координат, согласно (8) и при условии (9), становятся комплексными, а не действительными.

На рис. 3 показаны распределения интенсивности и фазы аБГ-пучка при небольшом параметре асимметрии c = 1. Остальные параметры расчёта: длина волны λ =532 нм, радиус перетяжки Гауссова пучка ω ₀= 100 λ ,

б)

г)

Рис. 3. Распределение интенсивности (негатив) (а, в) и фазы (б, г) аБГ-пучка третьего порядка (n = 3) при с = 1 на разных расстояниях z: 0 (а, б) и z0 (в, г)

На рис. 4 показаны интенсивность и фаза аБГ-пучка

нулевого порядка при следующих параметрах: длина волны λ =532 нм, радиус перетяжки Гауссова пучка ω 0 = 10 λ , масштабирующий множитель α = 1/(10 λ ), параметр асимметрии с = 10, границы расчётной области – 40 λ ≤ x , y ≤ 40 λ .

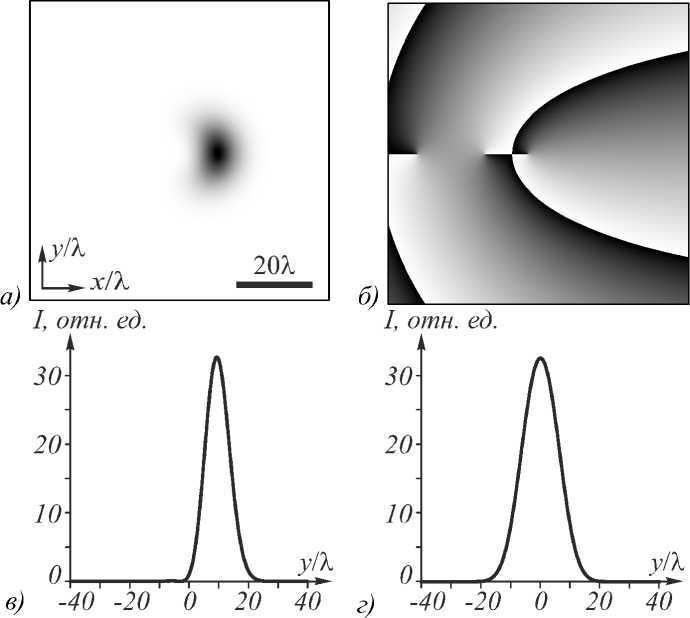
Рис. 4. Интенсивность (негатив) (а) и фаза (б) светового пучка (5) нулевого порядка (n = 0) в начальной плоскости, а также сечения интенсивности при z = y = 0 (в) и z = 0, x = xmax (xmax – координата максимума) (г)

В случае нулевого порядка аБГ-пучок (рис. 4) обладает интересным свойством: имеет максимум интенсивности вблизи оптической оси и ОУМ, отличный от нуля. Это свойство можно использовать при манипулировании диэлектрическими микрочастицами. Частица, которая по размерам в несколько раз больше основного максимума интенсивности пучка на рис. 4, может удерживаться этим максимумом интенсивности и одновременно вращаться вокруг своей оси.

J = Im j ff E * —r d r а _Ф1 , [ 2 Эф J

I = j| E * E r d r d ^ .

Подставив в (18), (19) комплексную амплитуду (3) при z =0, получим орбитальный угловой момент и

2. Фурье-спектр аБГ-пучка

Угловой спектр обычного БГ-пучка известен [4]:

An (p, Ф) = (-i)n exp

xIn r k^p^^) exp (inф), V 2 f J

k P®o |

J

x

где I n ( x ) – модифицированная функция Бесселя n -го порядка, ρ – радиальная координата в Фурье-плоскости, f – фокусное расстояние сферической линзы, формирующей пространственный спектр БГ-пучка. Рассмотрим линейную комбинацию, аналогичную (3), но состоящую из функций (14), получим угловой спектр аБГ-пучка:

An (P, Ф) = exp

k p® ₀ 2 f

x

г x Z p = 0

(-ic)p exp [i (n + p )Ф]i

p !

, ( kap®0 p V 2 f

.

Используя справочное соотношение [12]: г k

Z т!++v (x )=

= 0 ^k !

= x^v* ² ( x + 2 t ) ^{v /2} I_v ( V x ² + 2 tx ) ,

получим окончательное выражение для Фурье-спектра аБГ-пучка:

An (P, ф) = exp

x

k p®0

2 f

+ in ф x

^^^^^^

r

V ^+ 2 ce ^{( Ф-п /2)}

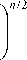
xIp {^[^ + 2c e-(Ф-п/2) ]},

где ^ = а k pw 2 /( 2 f ) . Угловой спектр (17) асиммет-

ричный: при φ = π/2 и на кольце фиксированного радиуса ρ = ρ₀ модуль амплитуды (17) имеет максимум, а при φ = – π/2 – минимум. Вид углового спектра (17) похож на вид амплитуды аБГ-пучка (5) (с точностью до замены функции Бесселя модифицированной функцией Бесселя), но повёрнут на 90 градусов. Поэтому асимметрия спектра (17) будет похожа на асимметрию аБГ-пучка (5).

3. Орбитальный угловой момент аБГ-пучка

Орбитальный угловой момент J_z (проекция ОУМ на оптическую ось) и суммарная интенсивность I светового пучка в плоскости, поперечной оптической оси, определяются по формулам [6]:

суммарную интенсивность аБГ-пучка:

J= 2„£   n x p=0 (P!)

г     r 2 r ² )

^x exp I-- T I ^J n + p ( ^{a r} ) ^{r d r},

0    V ®0 J

_т - c ^{2 p} г r 2 r ² )

1 = 2nZ TEE J exp I -    I Jn+p (ar)r dr.

p = 0 ( p ! ) 0      V ® 0 J

Интегралы в этих выражениях описаны в [12]:

г

J x exp (-px2) Jv (bx) Jv (cx) dx =

= ( 2 p ) ^- 1 exp

b2 + c211 Г bc |

4 p J v V 2 p J

Используя интеграл (22) и разделив (20) на (21), получим выражение для орбитального углового момента, нормированного на интенсивность:

J z = n ₊ y ^{c 2} p pIn + p ⁽ y )

I ^Z   ( p ! ) 2

У c² p I n + p ⁽ У ) p ^Z   ( p ! ) ²

- 1

где y = a ² ® 0 /4 . Выражение (23) дальше упростить не удаётся. Из (23) следует, что ОУМ аБГ-пучков больше n , так как все слагаемые рядов в (23) положительные. То есть с ростом параметра с растёт асимметрия аБГ-пучка и почти линейно растёт его ОУМ, как видно из рис. 5. Так как параметры а и c являются действительными положительными числами, то второе слагаемое в (23) может быть как целым, так и дробным положительным числом. Поэтому из (23) также следует, что аБГ-пучок нулевого порядка ( n =0) может иметь любой ОУМ. Заметим также, что в (23) масштабные параметры пучка Бесселя а и Гауссова пучка ω 0 входят в виде произведения, поэтому у разных аБГ-пучков, у которых а ю₀ = const, ОУМ будет одинаковым (при равных n и c ).

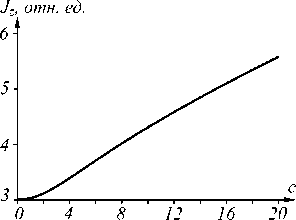
Рис. 5. Зависимость ОУМ от параметра асимметрии c при n = 3, to o = 10 Е а = 1/(10 А )

4. Взаимная неортогональность функций, описывающих семейство аБГ-пучков

Подобно тому, как был вычислен орбитальный угловой момент, можно вычислить скалярное произведение комплексных амплитуд двух ЭБ-пучков –

пучка n -го порядка с параметрами а и с и пучка m -го порядка с параметрами в и d :

ЛГО2_ ( d_

( E n а c , E m e d )     2 I c

n - m

X

X exp

-^ (а2 +₽2)

X

p ₊ n — m

. у (cd*)   2 x        [ m2 ав)

¹                    ------- p + max ( m,n ) I д I ,

p=0 p!(p + n - m\)!      v \ 4 )

модуляторе (без добавленной фазы линзы), и распределения интенсивности, зарегистрированные ПЗС-матрицей на расстоянии 850 мм ( б ), 900 мм ( в ) и 950 мм ( г ) от модулятора. Размерность модулятора составляет 1920×1080 пикселов , размер одного чувствительного элемента – 8 мкм. Фаза, представленная на рис . 7, имела размерность 1024×1024 пикселов и формировалась в центре модулятора. Таким образом, точный размер сформированного фазового распределения составлял 8,2 мм.

где I _v ( x ) - модифицированная функция Бесселя. Из выражения (24) видно, что в отличие от мод Бесселя [5] aБГ-пучки не ортогональны ни по масштабирующему множителю, ни по порядку функции Бесселя, ни по параметру асимметрии. В (24) параметры асимметрии c и d считались комплексными, а «*» – комплексное сопряжение.

Заметим, что аБГ-пучки при стремлении радиуса Гауссова пучка к бесконечности to o ^^ переходят в бездифракционные асимметричные элегантные моды Бесселя [13, 14].

5. Эксперимент

Схема экспериментальной установки представлена на рис. 6. В эксперименте был использован фазовый пространственный модулятор PLUTO VIS. Свет твердотельного лазера с длиной волны 532 нм расширяется коллиматором, ограничивается диафрагмой диаметром 8 мм. В результате получается равномерное распределение интенсивности, которое можно считать плоской волной. Далее свет проходит через светоделительный кубик и попадает на пространственный модулятор света, отражается от него и отклоняется светоделительным кубиком на ПЗС-камеру. На полутоновой модулятор с компьютера передаётся фаза для формирования аБГ-пучка в комбинации с фазой параболической линзы с фокусным расстоянием 960 мм.

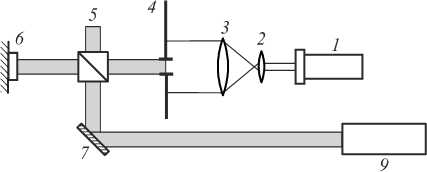
Рис. 6. Схема экспериментальной установки.

1 – твердотельный лазер с длиной волны 532 нм,

2, 3 – коллиматор, 4 – диафрагма, 5 – светоделительный кубик, 6 – модулятор PLUTO VIS, 7 – зеркало, 9 – ПЗС-камера

ПЗС-камера перемещается на небольшом отрезке в непосредственной близости от фокуса. На рис . 7 показаны фазовое распределение ( а ), сформированное на

в)

г)

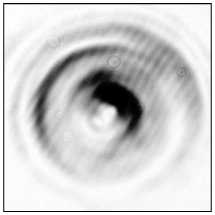
Рис. 7. Распределение фазы, сформированной на модуляторе PLUTO VIS (а), и распределения интенсивности (негативы), зарегистрированные на расстояниях от модулятора:

850 мм (б), 900 мм (в) и 950 мм (г)

На рис. 7 видно, что сформированное модулятором распределение интенсивности в форме полумесяца не только вращается в сходящемся лазерном пучке (за 100 мм пути пучок повернулся почти на 90 градусов против часовой стрелки), но и искажается. Это искажением связано с тем, что фазовое распределение (рис. 7 а ) только частично учитывает амплитудное распределение аБГ-пучка (5).

Заключение

Таким образом, в работе получены следующие результаты:

– получено новое решение параксиального уравнения Гельмгольца, описывающее трёхпараметрическое семейство асимметричных пучков Бесселя– Гаусса (аБГ-пучков), обладающих конечной энергией и описываемых функциями Бесселя первого рода целого порядка с комплексным аргументом ; при с =0 аБГ-пучки совпадают с обычными пучками Бесселя–Гаусса [1];

– распределение интенсивности аБГ-пучков имеет счётное число изолированных нулей, лежащих на горизонтальной прямой в начальной плоскости ( z = y =0); в местах этих нулей расположены оптические вихри, имеющие единичные топологические заряды и разные знаки с разных сторон от оптической оси (от центра координат); осевой ноль интенсивности имеет топологический заряд, равный порядку функции Бесселя;

• –    аБГ-пучки при больших параметрах асимметрии c >> 1 вращаются как единое целое при распространении в свободном пространстве: на расстоянии длины Рэлея они поворачиваются на 45° и ещё на 45° – за весь остальной путь; при небольших c пучки вращаются более сложным образом: на определённом расстоянии от начальной плоскости оптические вихри (изолированные нули интенсивности), которые присутствовали в сечении пучка, пропадают (кроме центрального нуля интенсивности) и на расстоянии длины Рэлея пучок может повернуться почти на 90°;

• –    аБГ-пучки имеют асимметричный угловой спектр, выражающийся через произведение Гауссовой функции на модифицированную функцию Бесселя с комплексным аргументом; вид этого спектра имеет асимметрию, аналогичную асимметрии аБГ-пучка, но повёрнутую на 90°;

• –    аБГ-пучки могут иметь целый и дробный ОУМ, который растёт с ростом номера n и почти линейно с ростом параметра c ; пучок нулевого порядка имеет максимум интенсивности, смещённый с оптической оси на величину с/ α , изолированные нули интенсивности и может обладать любым ОУМ в зависимости от выбора параметра асимметрии с ;

• –    аБГ-пучки не ортогональны ни по одному из параметров n , α , c ;

• –    экспериментально с помощью жидкокристаллического модулятора света сформирован сходящийся лазерный пучок, похожий на аБГ-пучок с распределением интенсивности в виде полумесяца, который повернулся почти на 90° против часовой стрелки.

Работа выполнена при поддержке грантов Президента РФ поддержки ведущих научных школ (НШ-3970.2014.9) и молодого доктора наук (МД-1929.2013.2), а также грантов РФФИ 13-07-97008 и 14-07-31092.