Вращение двухлепесткового лазерного пучка в ближнем поле вихревого микроаксикона

Вращающиеся световые поля, у которых при распространении в свободном пространстве вращается вокруг оптической оси распределение интенсивности в поперечном сечении, нашли применение в микроскопии при измерении локализации и ориентации отдельных молекул [1], при зондировании атмосферы и в беспроводных системах связи [2], в передаче информации под водой [3], а также в датчиках магнитного поля [4].

Впервые вращающиеся оптические вихри – когерентные световые поля с сингулярной фазой, которые вращаются при распространении в свободном пространстве, рассмотрены в [5]. В [5] было получено условие для номеров линейной комбинации мод Ла-герра – Гаусса (ЛГ), интенсивность которой как целое вращается при распространении. В [6] с помощью цифровой голограммы был сформирован вращающийся вихревой пучок, состоящий из суммы двух мод ЛГ с номерами (0, 0) и (4, 2) и имеющий распределение интенсивности в виде двух лепестков. В [6] экспериментально измерена угловая скорость вращения двухлепесткого пучка (ДЛП), которая оказалась непостоянной и на линейном участке была равна 0,008°/мкм. В [7] c помощью фазового дифракционного элемента были сформированы вращающиеся лазерные пучки, состоящие из двух мод Бесселя с топологическими зарядами –1 и –3. Скорость вращения ДЛП составила 0,006°/мкм. В [7] скорость вращения ДЛП, в отличие от [6], была постоянная. В [8] c помощью ДЛП точно (ошибка 1,6%) измерена глубина резкости изображения. В [9] предложено с помощью пространственного модулятора света формировать функцию рассеяния точки в виде двух лепестков, которые вращаются вокруг оптической оси при распространении в пространстве. С помощью оптимизационной процедуры был рассчитан фазовый элемент, эффективность которого при формировании ДЛП была равна 57%, хотя в эксперименте была достигнута эффективность только 37%. Сформированный ДЛП состоял из линейной комбинации многих мод ЛГ и формировался сферической линзой с числовой апертурой NA=0,71. При этом скорость вращения ДЛП вблизи фокуса в диапазоне от –1,5 мкм до 1,5 мкм составляла 50°/мкм. В [10] ДЛП, состоящий из двух пучков Бесселя, был сформирован с помощью жидкокристаллического модулятора. Скорость вращения была постоянная и равна 0,003°/мкм. В [11] предлагается методика формирования пучков, интенсивность которых вращается вокруг оптической оси с ускорением. В частности, с помощью модулятора сформирован ДЛП, состоящий из двух мод Бесселя с номерами 1 и 3, вращающийся со средней скоростью 0,0005°/мкм. В [12] теоретически исследуются ДЛП с неоднородной поляризацией. В [13] c помощью многомодового оптического волокна сформированы ДЛП с различным состоянием поляризации. В [14, 15] с помощью жидкокристаллического модулятора света сформированы ДЛП, состоящие из нескольких мод ЛГ. Скорость вращения ДЛП нелинейная, но на линейном участке длиной около 10 мм она была равна 0,15°/мкм. В этой работе исследуется, как аберрации фокусирующей линзы влияют на вращение ДЛП. В [16] исследуется вращение однолепесткового поля вблизи вихревого аксикона.

В работах [1–4] ДЛП применяются для решения конкретных практически важных задач. Так, в [1] предложена схема флуоресцентного микроскопа (глубина фокуса 2 мкм) с поперечным и продольным разрешением 250 нм и 500 нм соответственно и функцией рассеяния точки в виде двух вращающихся лепестков (скорость вращения около 50°/мкм). Предложенная схема позволила определить положение и ориентацию отдельной молекулы с точностью 34 нм. В [2] показано относительно стабильное распространение ДЛП (длина волны 809 нм) на расстоянии 1,6 км в Ерлангене (Германия). Параметр Фрида турбулентности атмосферы был равен 20 мм. В [3] исследуется распространение оптического вихря (длина волны 450 нм) с несколькими лепестками в канале с турбулентной водой (коэффициент затухания cz = 13). Коэффициент коррреляции пучка на выходе r = 0,98. В [4] вращающийся ДЛП пропускали через магнитооптический кристалл Bi4Ge3O12, сам кристалл помещали в магнитное поле, которое приводило к изменению угла поворота ДЛП. Чувствительность этого метода определения магнитного поля равна 28°/тесла.

Почти во всех перечисленных выше статьях ДЛП формируются с помощью пространственных модуляторов света. Но если не требуется изменять параметры пучка, то для формирования ДЛП более эффективно использовать дифракционный оптический микроэлемент. В данной работе с помощью простого спирального микроаксикона с топологическим зарядом m =2 и числовой апертурой NA = 0,60 сформирован ДЛП (длина волны 532 нм), интенсивность которого вращается в ближней зоне на расстоянии от 1 мкм до 4 мкм со скоростью 55°/мкм. Это скорость вращения ДЛП больше, чем во всех приведённых выше работах.

Теоретические основания

В [17] показано, что вращающиеся лазерные пучки можно сформировать с помощью любого известного в оптике вихревого модового базиса (моды Ла-герра – Гаусса, Бесселя, гипергеометрические моды, моды Бесселя – Гаусса и т.д.). Лазерный пучок будет вращаться, если он состоит из линейной комбинации специально подобранных мод. Причём скорость вращения для разных мод будет разная. Для вращающегося пучка, состоящего из линейной комбинации мод ЛГ, скорость вращения равна [17]:

Ф = - B arctg ( z / z 0 ) ,                               (1)

где

2( n - n ') + I m l - I m 'I

B =---------•—■—•—- = const, m - m'

Ф - полярный угол в поперечной плоскости пучка, z -продольная координата, направленная вдоль оптической оси, z ₀ = kw 2 /2 - длина Рэлея, к - волновое число света, w – радиус перетяжки Гауссова пучка, ( n, m ) – номера моды ЛГ, которые определяют порядок многочлена Лагерра L ^| _n ^{m |}( x ). В линейную комбинацию могут входить моды ЛГ, у которых номера ( n, m ) удовлетворяют условию (2). Из (1) видно, что на расстоянии z=z о пучок повернется на угол B п /4, и при больших z пучок повернется на B п /2. Кроме того, из (1) видно, что скорость вращения пучка не равномерная, а уменьшается с ростом z .

Аналогично можно сформировать параксиальный вращающийся световой пучок, состоящий из мод Бесселя. Комплексная амплитуда такого пучка будет равна:

E ( r , Ф , z ) =

= Е ^Cnm^Jm ^{(к -} n z ) exP ( - i ^{k -} n z / ^{2 +} im Ф ) ’ n , m

где С nm – произвольные комплексные коэффициенты, J_m ( x ) - функция Бесселя m -го порядка, a _n - коэффициент, определяющий масштаб функции Бесселя. Скорость вращения пучка с комплексной амплитудой (3) линейно зависит от z и равна:

Ф = kB , z /2, (4)

где

B , = -n----ⁿ- = const.

m - m '

Из сравнения (2) и (5) видно, что изменять скорость вращения пучка, состоящего из линейной комбинации мод ЛГ, можно дискретным способом, изменяя номера мод ( n , m ). Если вращающийся пучок состоит из суперпозиции мод Бесселя (3), то скорость вращения (4) можно менять непрерывно, изменяя масштабный коэффициент - _n . Другое преимущество мод Бесселя в том, что угол поворота пучка линейно зависит от пройденного расстояния z . Поэтому измерительное устройство на основе мод Бесселя легче калибровать.

В [1] предложена схема определения продольных координат объекта с разрешением большим, чем дифракционный предел, с помощью изображающей оптический системы с вращающейся двухлепестковой функцией импульсного отклика. Идея заключается в следующем: если объектная точка смещается вдоль оптической оси, то её изображение в виде двухлепестковой интенсивности будет вращаться вокруг оптической оси. Так как продольное разрешение идеальной оптической системы, определённое по полуспаду интенсивности, равно [18] (DOF, depth of focus )

DOF =

к

2 ( NA ) 2

а поперечное разрешение (FWHM, full width at half maximum ) равно

FWHM = — ,                     (7)

2 (NA)

где к - длина волны света, то измерять смещение двух лепестков интенсивности по окружности в поперечной плоскости можно с меньшим шагом (с большим разрешением), чем измерять смещение интенсивности в изображении вдоль оптической оси, в число раз:

DOF/FWHM = 1/NA .                  (8)

На практике точность метода ограничивается также шумом фотоприёмника [1] и аберрациями оптической системы [14]. Из (8) видно, что преодоление предела разрешения при измерении угла поворота

ДЛП тем больше, чем меньше числовая апертура изображающей оптической системы. Для микроскопов с высокой числовой апертурой (NA= 1) данный метод не позволяет преодолеть продольный дифракционный предел.

В данной работе мы с помощью дифракционного оптического изображающего микроэлемента (спирального аксикона [19] c топологическим зарядом m =2), изготовленного по технологии электронной литографии и ионного травления в стекле с показателем преломления, близким к 1,5, сформировали ДЛП, который поворачивается на угол 240 градусов на расстоянии от нуля до 4,5 мкм от микроэлемента. Средняя скорость вращения ДЛП – 55 °/мкм.

Моделирование

Винтовой (или вихревой) аксикон c топологическим зарядом m = 1 был рассмотрен в [16, 19]. Для формирования ДЛП потребуется вихревой аксикон (ВА) с топологическим зарядом m =2. На рис. 1 показан бинарный шаблон для изготовления такого дифракционного ВА. Период кольцевой решётки (рис. 1) равен T0=0,9 мкм, радиус ВА R = 15 мкм. Микроаксикон имеет 15 периодов. Параметры моде- лирования: показатель преломления материала акси-кона и подложки n = 1,5, длина волны λ =532 нм. Числовая апертура ВА NA= λ /Т = 0,56. Падающая на ак-сикон волна плоская с круговой поляризацией. Высота рельефа H = 0,47 мкм. Область моделирования – 15×15×5,1 мкм, шаг сетки – λ /30. Поперечные рас- пределения интенсивности рассчитывались за акси-коном на расстоянии до 4 мкм. Расчёт прохождения света через ВА и далее проводился с помощью известного метода FDTD, реализованного в коммерческой программе Fullwave (фирмы RSoft).

Рис. 1. Шаблон изготовляемого ВА с топологическим зарядом m = 2

На рис. 2 показаны поперечные распределения интенсивности на некоторых плоскостях.

Расстояние между лепестками приблизительно 0,8 мкм. Размеры каждого из лепестков на расстоянии 4 мкм (рис. 2г) по полуспаду интенсивности равны: минимальный FWHM=0,438 мкм (0,824λ) и максимальный FWHMy = 0,57 мкм (1,07λ). Рассматриваемый аксикон работоспособен до расстояния 9 мкм. Это видно из рис. 3, на котором показана зависимость интенсивности вдоль оптической оси аналогичного акси-кона, только с топологическим зарядом m =0. Заметим, что длина, на которой аксикон проявляет свойство «бездифракционности», не зависит от m, а определяется только радиусом аксикона R и его числовой апертурой NA. Глубина фокусного пятна на рис . 3 составила DOF=5,96 мкм по полуспаду интенсивности.

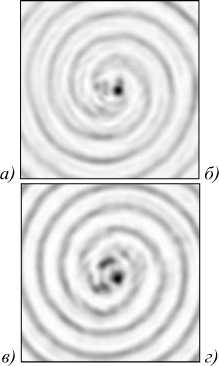
Рис. 2. Распределения интенсивности, рассчитанные на расстояниях от поверхности ВА: 1 мкм (а), 1,5 мкм (б), 2 мкм (в) и 4 мкм (г) (негативные изображения).

Размеры кадров – 8×8 мкм

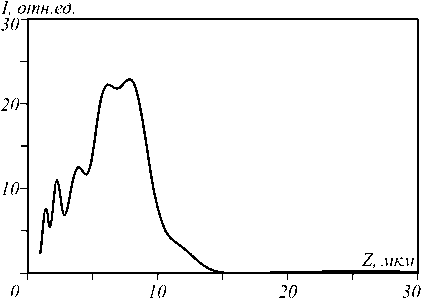
Рис. 3. Зависимость интенсивности на оси от расстояния z для аксикона с m = 0

На рис. 4 приведена зависимость угла поворота лепестков на рис. 2 от расстояния по оcи z .

Из графика на рис . 4 видно, что максимальное отклонение одной точки данных от усредненной линии составляет не более δ = 10°. Средняя скорость вращения максимумов ДЛП равна 55,43°/мкм. Теоретическая скорость вращения, полученная на основе (4), равна:

ϕ k α ² z 2 m .

Для аксикона параметр α =sin θ =( λ / T ). В моделировании и эксперименте следующие параметры: λ =532 нм, m =2, Т = 0,95 мкм. Поэтому скорость вращения согласно (9) равна 53°/мкм. Это значение хорошо согласуется со скоростью (55,43°/мкм), полученной при строгом моделировании векторной дифракции лазерного пучка на ВА.

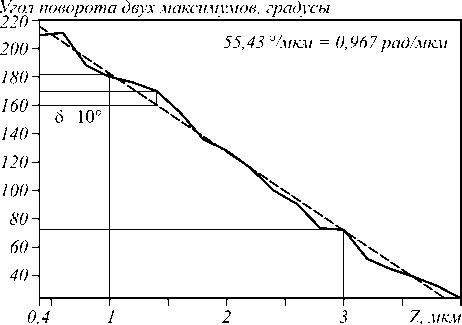
Рис. 4. Скорость вращения ДЛП в диапазоне z от 0,4 мкм до 4 мкм: сплошная прямая – результаты расчёта с шагом по оси z = 0,2 мкм, а пунктирная прямая получена путём усреднения наклона линейных участков ломаной сплошной кривой

Изготовление вихревого аксикона

С помощью шаблона (рис. 1) микроаксикон изготавливался по технологии электронной литографии и ионного травления.

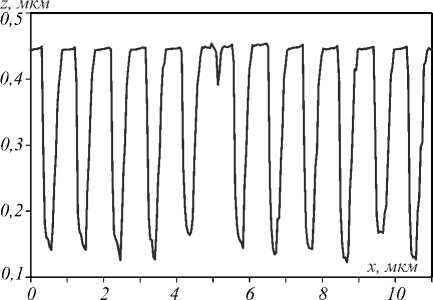
На рис. 5 показан рельеф центральной части ВА, измеренный на атомно-силовом микроскопе. Из рис. 5б видно, что период аксикона равен Т = 0,95 мкм, высота рельефа H =470 нм. Далее с помощью скани- рующего ближнепольного микроскопа измерялось прохождение света с круговой поляризацией и длиной волны λ =532 нм через ВА с топологическим зарядом m =2. Круговая поляризация получалась из линейной после прохождения четвертьволновой пластинки. Поворотом четвертьволновой пластинки обеспечивалась смена направления поляризации с левой на правую. На рис. 6 приведены поперечные распределения интенсивности, измеренные с помощью сканирующего оптического ближнепольного микроскопа на расстояниях от вихревого аксикона 1 мкм (а), 1,5 мкм (б) и 2 мкм (в).

Из рис. 6 видно, что за 1 мкм пучок повернулся почти на 76 градусов. Отличия в распределении интенсивности ДЛП с правой и левой круговой поляризацией незначительное. На рис. 7 показаны сечения интенсивности ДЛП на одном и том же расстоянии от поверхности ВА.

По данным измерения интенсивности ДЛП на разных расстояниях получен график зависимости угла поворота ДЛП от расстояния z (рис. 8). Моделирование методом FDTD показывает линейный рост угла поворота, в то время как эксперимент демонстрирует нелинейное изменение. Из рис. 8 видно, что скорость вращения не совсем линейная и хорошо совпадает с расчетом (55°/мкм) только в диапазоне расстояний z от 1,5 мкм до 3 мкм.

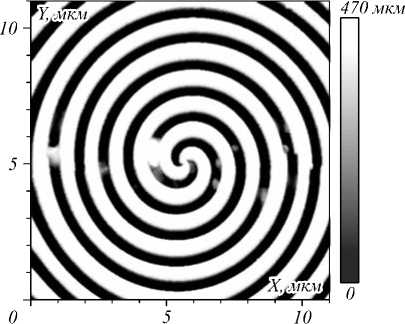
Рис. 5. Рельеф изготовленного ВА с m = 2 (а) и его сечение вдоль оси y (б), измеренные на атомно-силовом микроскопе

а)

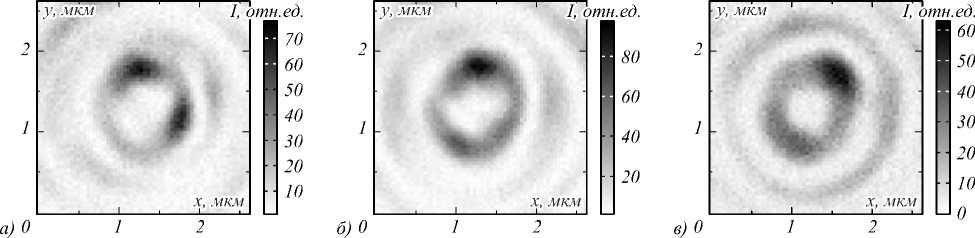
Рис. 6. Распределение интенсивности на расстоянии до поверхности ВА 1 мкм (а), 1,5 мкм (б) и 2 мкм (в) для пучка с правой круговой поляризацией

До расстояния z = 1,5 мкм скорость вращения (66 °/мкм) больше, чем рассчитанная (рис. 4), а после расстояния z = 3 мкм скорость вращения меньше (34 °/мкм), чем рассчитанная. Заметим, что на рис. 8 приведены данные двух экспериментов, проведённые с двумя аксиконами, которые отличались друг от друга только глубиной рельефа (на 10 %).

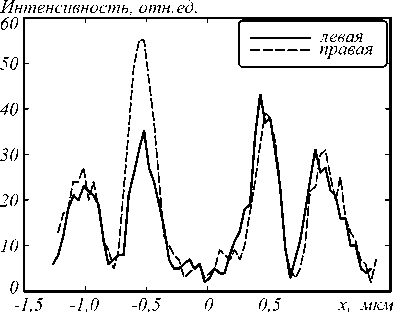
Рис. 7. Сечение интенсивности вдоль оси x для левой

(сплошная кривая) и правой (пунктирная кривая) круговой поляризации на расстоянии 1 мкм от ВА

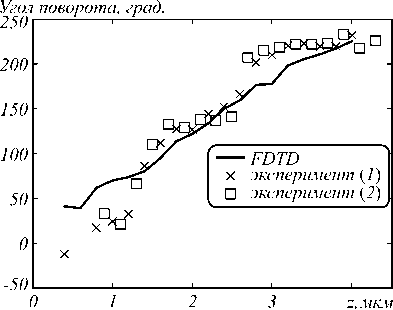
Рис. 8. Зависимость угла поворота максимумов ДЛП от расстояния до поверхности ВА.

Кривая – моделирование методом FDTD, маркеры – измерения для двух разных образцов вихревых аксиконов

Заключение

В работе теоретически, численно и экспериментально показана возможность с помощью простого и хорошо известного компонента микрооптики (вихревого аксикона) с невысокой числовой апертурой (0,6) формировать вращающиеся двухлепестковые лазерные пучки (55°/мкм) на некотором расстоянии (от 0,5 мкм до 4,5 мкм) вблизи аксикона. По измерению поворотов лепестков интенсивности в поперечной плоскости можно определить продольное смещение исследуемого объекта с преодолением продольного дифракционного предела. И чем меньше числовая апертура оптического элемента, формирующего двухлепестковой вращающийся пучок, тем эффективнее применение данного метода. Изготовленный вихревой аксикон может быть использован в микроскопии при измерении локализации и ориентации отдельных молекул, при зондировании атмосферы и в беспроводных системах связи, в передаче информации под водой, а также в датчиках магнитного поля.

Работа выполнена при поддержке Российского научного фонда (грант 18-19-00595) в части «Изготовление вихревого аксикона», Федерального агентства на- учных организаций (соглашение № 007-ГЗ/Ч3363/26) в части «Теоретическое основание» и Российского фонда фундаментальных исследований (грант 16-47630483) в части «Моделирование».