Вращение эллипсоидальной диэлектрической частицы в фокусе гауссова пучка с круговой поляризацией

Изучение силы, действующей со стороны света на микро- и нанообъекты, до сих пор вызывает интерес исследователей [1–9], который проявляется как для двумерного случая [10], так и для трёхмерного [11, 12, 13]. Для оценки силы, действующей на частицу, размер которой значительно превышает длину волны, расчёты можно проводить в приближении геометрической оптики. Такие расчёты, как правило, используют метод трассировки лучей Монте-Карло: лучи от источника исходят случайным образом, формируя в целом заданное распределение потока света [1,3]. Однако, если объекты соизмеримы с длиной волны или меньше её, расчёт силы основывается на строгих методах, например, на использовании тензора напряжения электромагнитного поля Максвелла [3]. Рэлеевские частицы, размер которых имеет порядок 1/20 длины волны света, почти не изменяют распределение поля, и расчёт сил для таких частиц можно проводить на основе дипольного приближения [15, 16]. Для объектов с простой формой (шар) в известных полях существуют и аналитические решения [17, 18].

Знание силы действия света на частицу лежит в основе создания оптических пинцетов [19,20]. Чаще всего оптические пинцеты используются для манипуляций биологическими объектами, захвата и удержания клеток, изучения их механических свойств, раз- деления клеток и т.д. Например, в [11] авторы исследовали создание оптических ловушек на основе лазера с фокусным пятном в виде эллипса для кровяных клеток. В [21] исследователи провели эксперименты по захвату как микрочастиц из кремния диаметром 2,58, 5,06, 9,63 мкм, так и яйцеклеток китайского хомяка диаметром 15 мкм в двухлучевую оптическую ловушку. В [22] авторы с помощью оптического пинцета предложили измерять такие характеристики кровяных клеток, как вязкость мембраны, адгезию клеток, zeta-потенциал и размер зарядов, сформированных вокруг клеток в электролите. Однако интерес также представляют и небиологические микро- и нанообъекты. Например, в [23] были рассмотрены силы, действующие на пару золотых нанопроводов.

Кроме силы, действующей на частицу в световом поле, интерес представляет также момент этой силы [24]. Например, авторы в [13, 25, 26] изучали момент, действующий на эллиптическую частицу в трёхмерном случае, однако их расчёты справедливы только для рэлеевских частиц. Авторы в [27] использовали геометрооптическое приближение для расчёта момента силы на металлизированные частицы. В [28] численно и экспериментально была изучена подвижность похожих на стержни частиц, возникающая из-за момента силы, действующего со стороны света. Однако расчёты проводились в дипольном приближении [29]. Но для более сложных частиц, имеющих размер порядка длины волны и более, дипольное приближе- ние не является точным. В целом из приведённых статей видно, что расчёт момента силы строгим методом на основе поля дифракции для частиц с размером более длины волны не проводился. Такой метод требует точного расчёта поля и является вычислительно трудоёмким. Кроме того, не был исследован момент силы в фокусе поля с круговой поляризацией, однако данное поле является одним из самых простых способов передачи момента частице в оптической ловушке.

В данной работе рассмотрено поведение эллипсоидальных диэлектрических частиц в области острого фокуса волны с круговой поляризацией. Расчёты проведены на основе поля дифракции, полученного методом FDTD (пакет Rsoft FullWAVE), далее сила и момент силы рассчитывались с использованием тензора напряжений Максвелла. Данный подход позволяет рассчитать силу и момент силы, действующие на частицу произвольной формы в любых когерентных световых полях. Показано, что в фокусе сферической волны с круговой поляризацией на эллипсоид относительно его центра действует момент силы, который будет стремиться вращать его вокруг оптической оси. Это справедливо, когда его наибольший диаметр лежит в поперечной к оптической оси плоскости. При смещении эллипсоида с оптической оси возникает сила со стороны света, препятствующая этому смещению, то есть на оптической оси частица будет находиться в оптической ловушке.

M = ^ [rx(°-n)]dS,

S

где r – радиус-вектор от точки A ( x , y , z ) до точки интегрирования на поверхности S , n – внешний вектор нормали к поверхности S , A – точка, относительно которой вычисляется момент M , о - тензор напряжений электромагнитного поля Максвелла, компоненты которого в системе СГС имеют вид [14]:

о = ± f E- . H4п

V

5 k

)

- EE - H i H k

J

где E i , H i – компоненты электрического и магнитного полей, 5 _ik - символ Кронекера ( 5 i = _k =1, 5 i ^ _k =0).

Далее рассмотрим вычисление момента силы более подробно. Произведение тензора напряжений Максвелла на нормаль можно записать в виде:

( о	- n )=	[ о ii ^i	о ij о jj	° ,. ° j.	f n.' n y	=
		о ki	о kj	о kk _	V n z J
[	о ii n x	+ о ij	П у +о	k n	T x
=	O ji n x	+о ^	П у +о	jk n z	= T у

о kin + о чПу + о kkn ]  V tz J

Тогда подынтегральное выражение в (2) примет вид:

Теоретическое основание

	" i	j	k
r х ( о- n ) =	r x	r y	r z
	_T x	T у	T z

На рис. 1 представлена схема расчёта момента силы на произвольную микрочастицу, находящуюся в световом поле.

= i (Гу T z - r T y) + j (r T y - rx T z) + k (Гх T у - r T x).

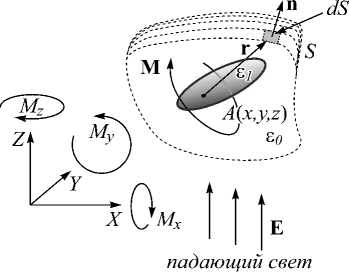
Рис. 1. Схема рассматриваемой задачи

Пусть на произвольную микрочастицу с диэлектрической проницаемостью £ 1 в среде с диэлектрической проницаемостью £ 0 (будем считать её равной 1) падает когерентное световое поле произвольным образом. Тогда сила действия света F и момент M , действующий со стороны света на микрочастицу относительно произвольной точки A , будут равны [30, 31, 32]:

F = -ф(о-n)dS,

S

Таким образом, проекции момента M вокруг осей координат можно записать в виде:

Mx = <£ (Гу Tz - rz T у) dS,

S

M y = ф ( r_z T у - r y T z ) d S ,                            (6)

S

M z = ^lf ( r x T у - Г у t x ) d S .

S

Для электромагнитных полей, колеблющихся с оптической частотой, имеет смысл только усредненное по времени значение момента (2) за период колебания:

(M) = (<^ [ r x ( о - n ) ] d s\ .                         (7)

S

При усреднении по времени за период T 2 л / to тензора о учтём, что:

E ( x , t ) = Re { E ( x ) e ™ * } ,

H ( x , t ) = Re { H ( x ) e ™ * } ,

( Re ( E ( x , у , z ) e ™ t ) Re ( E j ( x , у , z ) ё ™ t )) =            ⁽⁸⁾

= ]2 Re ^[ E ( ^x , у , z ) E * ( x , у , z ) ] .

Подставляя (4) в (6) и учитывая (8), окончательно получим для проекции момента M_x :

M_x = — (6 (Re (e₀ EE * + HH *) r - Re (e₀ E_ZE * + HH *) r )d S_x - x 8 ^ s         0 y x y x) *        \ 0 * x * x) y) x

- —4 Re(e₀ E_ZE * + HH *) r + r * (e E 8 n S V V ⁰ * ^y * ^y) ^y 2 01 ^x l

-

^e o | E y | ^{+ e} o

|E * |² +| H, |² -| H y\ ² +| H_z |²)jd S y +

+--8n

j)[ Re (eo EyE* + HyH*) r + rr s V                           2

(eo Ex I2 +Eo |Ey(

-

e o

|E *\ ² +| H x |² +| H y |² -| H *\ ²)jd S * .

Аналогично находятся проекции вектора момента относительно остальных двух осей M y , M z .

Расчёт момента силы в фокусе поля с линейной поляризацией

На рис. 2 показана зависимость момента силы M y , действующей со стороны света на трёхмерную наночастицу, имеющую форму эллипсоида. Эллипсоид задавался двумя радиусами – R min и R max как функциями от относительного радиуса R ref :

R ref

R min     ^/3 ,

R max

Показатель преломления эллиптической частицы был равен n = 1,5, показатель преломления среды n 0 = 1. Падающее поле – линейно-поляризованный сфокусированный Гауссов пучок с диаметром перетяжки ® o = % =633 нм:

E x = E o exp

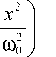
поле в фокусе Z =2,25 мкм = 3,55 % .

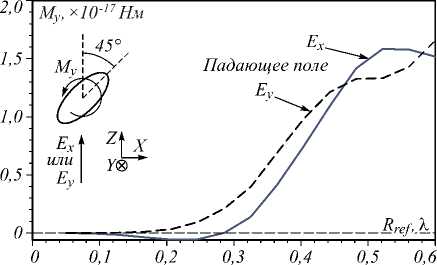
Рис. 2. Зависимость момента силы, действующей на эллипсоид с показателем преломления n=1,5 со стороны Гауссова пучка от относительного радиуса R_re f . Эллипсоид расположен в центре перетяжки Гауссова пучка с наклоном 45°

В начальной плоскости падающий пучок имел ширину по полуспаду интенсивности

FWHM_source= 1,5 мкм = 2,36 % .

Мощность падающего пучка была равна 100 мВт. Моделирование проводилось с помощью FDTD- метода в программном пакете FullWAVE, шаг сетки был взят равным %/5o по всем трём осям.

Из рис. 2 видно, что при расположении вектора падающего электрического поля и наклона частицы в одной плоскости (XZ) частица малых размеров стремится занять положение, когда её наибольший радиус R max перпендикулярен оптической оси. Это согласуется с выводами в работах [26,30], где было исследовано вращение относительно центра рэлеевских частиц в сфокусированных пучках. Величина этого момента силы имеет порядок io^-17 Н - м, что также согласуется с порядком момента силы в [30] с учётом того, что там приводятся данные для двумерного случая: тогда момент силы имеет размерность (Н /м) - м на погонный метр длины для бесконечного цилиндрического объекта. При этом для размеров частицы порядка 1 мкм величина момента получается больше в 10⁶ раз, так как интегрирование проводится по двумерному контуру. А в [26] авторы рассматривали момент силы, действующий на частицу с размером приблизительно 0,1 % и находящуюся в точке равновесия, что показало аналогичное поведение наночастицы при идентичной поляризации падающего пучка: эллиптическая частица стремится также расположиться или вдоль пучка, или поперёк него в зависимости от поляризации падающего света. В случае с падающей волной E y рэлеевская эллиптическая частица стремится занять положение вдоль оптической оси, что также согласуется с [30]. Но при этом следует отметить, что в трёхмерном случае характер поведения момента силы несколько другой: с увеличением относительного радиуса R ref более 0,4 % подобного сильного (как получили авторы в [30]) падения момента M y не происходит, хотя в случае падающего поля E y на графике момента M y и наблюдается некоторый провал начиная с радиуса R_re f >o,45 % , а при падающем поле E_x - начиная c R ref >o,52 % .

Расчёт силы и момента силы в фокусе поля с круговой поляризацией

Отдельный интерес представляет собой поведение микро- и наночастиц в сфокусированном поле с круговой поляризацией. Ранее была показана спин-орбитальная конверсия в фокусе пучка с круговой поляризацией [33], из которой следует, что диэлектрическая (без поглощения) частица, попавшая в фокус плоской волны с круговой поляризацией, будет вращаться вокруг оптической оси, если её центр расположен на оптической оси. На рис. 3 показана зависимость момента Mz вокруг оптической оси для эллипсоидальной частицы в фокусе такого поля от размеров частицы, диаметры которой удовлетворяют соотношению:

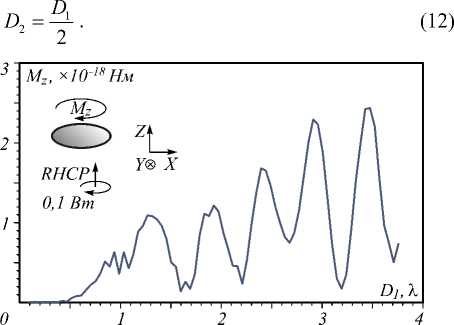
Рис. 3. Зависимость проекции момента Mz от наибольшего диаметра D1 эллипсоидальной частицы в фокусе сходящейся сферической волны с диаметром 8 мкм с правой круговой поляризацией

На частицу падала сферическая волна ( r = 6,06 мкм) с правой круговой поляризацией:

(■ (      п Il

• E, = exp i - kr + - to t , x

ll 2 JJ                  (13)

Ey = exp (i (-kr -tot)), то есть при круглой апертуре диаметром d = 8 мкм фокусное расстояние составляло f =4,55 мкм (NA=0,65), частица располагалась в фокусе пучка. Длина волны равна % = 532 нм, частица с показателем преломления n = 1,5 находилась в воздухе (n0= 1), шаг сетки при моделировании был взят %/50 по всем трём осям. Из рис. 3 видно, что при увеличении диаметра на каждую половину длины волны возникает максимум момента Mz, при этом в минимумах значения момента Mz примерно на порядок меньше, чем в максимуме. При этом момент направлен в ту же сторону, куда направлено вращение вектора электрического поля в падающем пучке, что также согласуется с экспериментальным результатом в [33].

На рис. 4 показана зависимость проекций моментов M_z , M_y и проекций сил F_x , F_y , F_z от смещения частицы в поперечной плоскости вдоль осей X и Y .

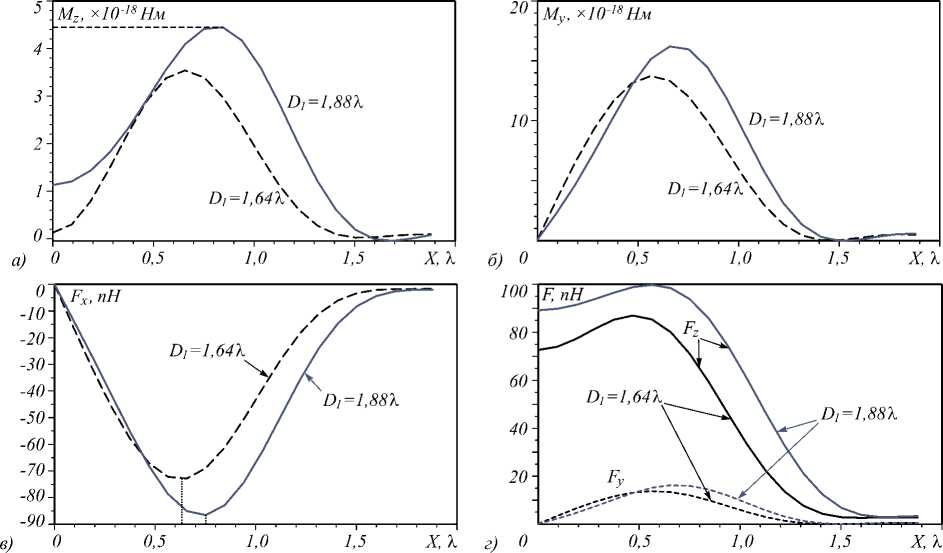
Рис. 4. Зависимость проекций моментов Mz (a), My (б) и проекций сил Fx (в), Fy, Fz (г) от смещения частицы вдоль оси X

Моделирование проводилось для частиц двух размеров D 1 = 1,64% и D 1 = 1,88%, попадающих на рис. 3 в минимум и максимум момента Mz. Из рис. 4 видно, что при смещении частицы вдоль оси X момент вокруг оптической оси Mz продолжает действовать на частицу с тем же знаком, что и в центре, причём до расстояния X = 0,7...0,8% он растёт, далее по мере выхода частицы из пучка он уменьшается. Кроме того, при смещении частицы вдоль оси X относительно её центра возникает момент My. Момент Mx равен нулю, так как эллипсоид симметричен вокруг наибольшего диаметра. При смещении частицы появляется поперечная проекция силы Fx, которая стремится переместить частицу назад, в максимум интенсивности пучка. Для частиц диаметром D 1 = 1,64% и D 1 = 1,88% максимального по модулю отрицательного значения проек- ция Fx достигает в двух точках приблизительно X = 0,63λ и X = 0,75λ. Разность между ними соответствует половине разности в диаметрах D1 частиц. Еще при смещении частицы возникает проекция силы Fy, которую, поскольку пучок осесимметричен, можно рассматривать как азимутальную силу. Она направлена в положительную сторону оси Y. Наличие положительной проекции силы Fz объясняется тем, что расчёт производился в центре перетяжки пучка вдоль оси Z, а не в точке равновесия.

На рис. 5 показан момент, действующий на частицу с диаметром D ₁ = 1, 88λ = 1 мкм ( λ =532 нм) в координатах (0,75 λ ;0). Видно, что момент не является постоянным и не зависит от угла поворота, как в центре координат. Частица имеет две точки равновесия, неустойчивое ( M_z =0 при ϕ = 89,53°) и устойчивое равновесие при угле ϕ = 173°.

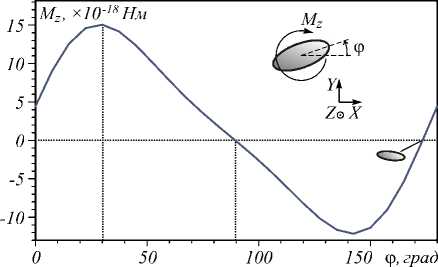
Рис. 5. Зависимость момента от угла поворота эллиптической частицы, расположенной в координатах X=0,75λ, Y=0

То есть до попадания в центр координат частица может повернуться до положения равновесия, но вращаться на полный оборот не сможет.

Таким образом видно, что, если расположить эллиптическую частицу близ фокуса пучка с правой круговой поляризацией, она будет поворачиваться до положения устойчивого равновесия и перемещаться в поперечной плоскости в центр фокусного пятна по спирали, закрученной к центру влево (если смотреть с положительной стороны оси Z ). После того, как частица окажется в центре фокусного пятна, она будет испытывать момент | M z | в поперечной плоскости меньше в несколько раз, чем момент | M z |, возникающий ещё до попадания в центр фокусного пятна (рис. 4 а ). Но этот момент перестанет зависеть от угла ϕ , то есть частица сможет вращаться на полный оборот. Для сравнения – сила тяжести такой эллиптической частицы из оргстекла (плотность ρ = 1190 кг/м³) имеет порядок F g = 1,22 ⋅ 10 ^–14 Н. То есть сила со стороны света на частицу при рассматриваемой мощности пучка на 2–3 порядка больше (рис. 4 в , г ).

Все расчёты выше приведены для случая диэлектрической частицы без мнимой части показателя преломления. Если частица будет иметь коэффициент затухания, момент относительно оптической оси Mz бу- дет больше. На рис. 6 показана зависимость момента Mz от мнимой части показателя преломления n. Здесь эллипсоидальная частица также расположена на оптической оси с наибольшим диаметром вдоль оси X.

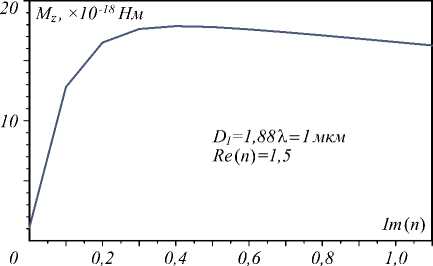
Рис. 6. Зависимость момента Mz от мнимой части показателя преломления частицы. Частица расположена на оптической оси

Все параметры на рис. 6 те же, что и для рис. 3, в том числе и действительная часть показателя преломления. Наибольший диаметр частицы был постоянным и равен D 1 = 1,88 λ . Видно, что в случае добавления поглощения момент растёт приблизительно до значения Im( n )=0,4, далее постепенно спадает.

Заключение

В работе рассмотрены силы и моменты сил, действующие в фокусе сферической волны с линейной и круговой поляризациями на эллипсоидальную диэлектрическую частицу. В фокусе сферической волны с круговой поляризацией на эллипсоид относительно его центра действует момент силы, который будет стремиться вращать его вокруг оптической оси. Пока эллипсоид смещён от оптической оси, проекция момента силы на оптическую ось принимает разный знак при вращении частицы на 360°, то есть частица имеет положение устойчивого равновесия. При расположении эллипсоида на оптической оси проекция момента силы на оптическую ось принимает один знак, что при отсутствии сопротивления движению из-за других факторов (трение, вязкость и т.д.) приведёт к непрерывному вращению вокруг своего центра, находящегося на оптической оси.

Работа выполнена при поддержке Российского научного фонда в частях «Теоретическое основание», «Расчёт момента силы в безвихревом поле» (грант 1819-00595), Российского фонда фундаментальных исследований (грант 18-29-20003) в части «Расчёт силы и момента силы в вихревом поле», а также Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в частях «Введение» и «Заключение».