Вращение лазерных пучков, не обладающих орбитальным угловым моментом

E ⁽ x , У ) = E C ⁽ n , m ^)T - ⁽ x , У ), ⁽¹⁾ n , m

2( n - n') + |m| - |m '| B =-------------

m - m'

= const,

где ( n,m ) и ( n’,m’ ) номера двух любых мод из линейной комбинации (1). Постоянная величина B /4 равна числу оборотов, которое совершает многомодовый пучок ЛГ от z= 0 до z=∞ . Причем половину этих оборотов пучок совершит на расстоянии от z= 0

k tog                               Z П до z=z0, где z0 = -0^- - расстояние Рэлея, k=2n/k -

волновое число света. В [11] получено уравнение для проекции на ось z линейной плотности орбитального углового момента линейно поляризованно-

го лазерного пучка на единицу мощности, состоящего из суперпозиции мод ГЛ (1):

^ m\C (n, m )|2 n,m wJ , =----------- sIC(n,m )

где C ( n,m ) – комплексные коэффициенты с номерами n и m , причем m – азимутальный индекс,

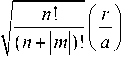
m

X r2

--- + im m 2 a ²

V nm ⁽ x , У ) = a ^{- 1}

x L m n

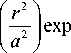
to

где a = —0=, to o - радиус перетяжки Гауссового пуч-2

ка, ( r , φ) – полярные координаты, L^m_n ( x ) – присоединенные многочлены Лагерра. В [7] приведено условие на номера мод в уравнении (1), при которых интенсивность в поперечном сечении многомодового пучка ЛГ будет вращаться при его распространении вдоль оси z :

где w – циклическая частота света. Из уравнений (1)-(4) следует:

• 1)    фазы коэффициентов C ( n,m ) не влияют на значения B и J z , но влияют на вид интенсивности светового поля из уравнения (1) I ( x, y, z ) = | E ( x, y, z )|²;

• 2)    число оборотов согласно уравнению (3) при вращении пучка (1) зависит только от комбинации номеров мод ( n, m ) и не зависит от выбора значений коэффициентов C ( n, m );

• 3)    ОУМ (4) определяется только азимутальными номерами m мод ЛГ и значениями модулей коэффициентов C ( n , m ) и не зависит от выбора номеров n . Поэтому с помощью подходящего выбора комбинации номеров ( n, m ) и модулей коэффициентов C ( n , m ) можно реализовать различные варианты сочетаний значений B и J z .

На рис. 1 приведены численные примеры. В первой строке показаны распределения интенсивности 4-хмодового пучка ЛГ с коэффициентами C (12,0)=1, C (11,2)=1, C (10,-4)= i , C (9,6)=1. Такой пучок не вращается ( B =0), но имеет положительный ОУМ ( wJ z =1).

Во второй строке рис. 1 показаны распределения интенсивности 5-ти модового пучка ЛГ с коэффици-

ентами C (2,2)= i , C (3,1)=1, C (4,0)=-1, C (4,-2)=1, C (4,-4)=1. Такой пучок вращается влево ( B =-1) и имеет отрицательный ОУМ ( wJ_z =-3/5).

В третьей строке рис. 1 показаны сечения интенсивности 3-х модового пучка ГЛ с коэффициентами C (10,-2)=1, C (8,0)=1, C (4,2)=1. Этот пучок вращается влево ( B =-3), но не обладает ОУМ ( wJ z =0).

И в четвертой строке рис.1 показан 2-х модовый пучок ЛГ с коэффициентами C (1,-1)=1, C (9,1)=1. Этот пучок вращается вправо ( B =8) и также не обладает ОУМ ( wJ z =0). Параметры моделирования: длина волны света X=633 нм; радиус перетяжки фундаментальной моды ЛГ ю₀ =0,1 мм; размер каждой картинки на рис. 1 - 1ммх1мм; расстояние, на котором рассчитывались интенсивности на рис. 1 (слева направо) z =30 мм, z =40 мм, z =50 мм.

Рис. 1. Распределения интенсивности (негатив) в поперечном сечении многомодовых пучков ЛГ, рассчитанных на расстояниях z=30 мм (1 столбец), z=40 мм (2 столбец), z=50 мм (3 столбец) для: 4-х модового (1 строка), 5-ти модового (2-строка), 3-х модового (3 строка) и 2-х модового (4 строка)

Для суперпозиции мод Бесселя (1) вместо выражения (2) запишем:

^ nm ⁽ x , У ) = [7™ RJ m ⁽ Y n ) ] X х J m ( k a n r )exp( im ф ),

Y„

где a = cos 9 = — , 0„ - угол наклона к оси z кони-nnkR ческой волны, Jm(x), J’m(x) - функция Бесселя и ее производная, уn — корень функции Бесселя. Моды Бесселя (5) нормированы на единицу в круге радиуса R. Лазерный пучок (1), состоящий из мод Бесселя будет вращаться [12] на конечном расстоянии от исходной плоскости (z=0) при условии, что номера мод (n,m), входящих в суперпозицию (1) будут удовлетворять условию:

Число B 1 /2 равно числу оборотов, которые совершает интенсивность в сечении пучка на расстоянии равном одной длине волны X. Проекция на ось z линейной плотности орбитального углового момента лазерного пучка на единицу мощности, состоящего из суперпозиции мод Бесселя рассчитывается с помощью уравнения (4). Из уравнений (4) и (6) следует, что подбором номеров ( n, m ) можно сформировать пучки Бесселя, обладающие вращением интенсивности в поперечном сечении ( B 1 ^ 0), но имеющие нулевой орбитальный момент ( J_z = 0). На рис. 2 показаны распределения интенсивности 2-модового пучка Бесселя с коэффициентами C ( a ₅,3)=1 и C ( a ₁₀,-3)=1. Такой пучок вращается влево ( B 1 = - 12,5x10 '8 ) и не обладает орбитальным моментом ( J_z= 0). Параметры расчета: X=633 нм, a ₅ = 5x10^-4 , a ₁₀ = 10x10^-4 , размер картин дифракции на рис.2 - 5x5 мм.

а                 б                 в

Рис. 2. Распределения интенсивности в сечении 2модового пучка Бесселя, рассчитанные на разных расстояниях z от начальной плоскости:

1 м (а), 2 м (б) и 3 м (в)

В [13] приведен ортогональный базис функций, удовлетворяющих параксиальному уравнению распространения. Эти функции можно рассматривать как еще один тип параксиальных световых мод свободного пространства. Мы называем их гипергеометрические (ГГ) моды, так как они описываются через гипергеометрические функции. Как и моды Бесселя ГГ-моды обладают бесконечной энергией, и поэтому на практике их можно сформировать с помощью амплитудно-фазового фильтра или цифровой голограммы с кольцевой апертурой. Поэтому ГГ-моды будут сохранять свои модовые свойства только на конечном расстоянии вдоль оптической оси.

Для суперпозиции ГГ-мод (1) вместо (2) и (5) запишем ( R » 1 ) :

- у

^ nm ^{( Х} , У ) = ( ^{2 П} r ^{2 1П R} ) ^{2 X}

( п n)

х exp I i In r + im ф| , n = 0, ± 1, ± 2,...

I In R)

Эти моды будут ортонормированны в кольце с радиусами R и R ¹:

R

J ^ nm (r, Ф^'Л r, ф) r dr dф = 8 „,8„.,

R - 1

где 8nn. - символ Кронекера. В зоне дифракции a2 - a2, B1 =--------= const.

m - m '

kr1 _

Френеля мода (7) имеет вид ( R ^« , x =     ):

2 z

^ nm ⁽ r , Ф , z ) =

2n |m|

i Y- 1

( 2 z ) ² x

! I k J

in

x exp —(- |m| + iy-1) + ix + im^

хГ

i n

^ |m| + iY +1) l^-J1F1

' |m| + i Y +1

I 2

m

x2 x

, |m| +1; -ix

nn где Y =     , lnR

₁ F₁ ( a , b ; x ) - конфлюэнтная гипергео-

том ( J_z= 0). Параметры расчета: Х=633 нм, Y o = 0 , Y 3 = 13,597, размер картин дифракции на рис. 3 -4×4 мм.

Заметим, что в [14] исследован частный случай ГГ-мод при y = - i , которые формируются с помощью спиральной фазовой пластинки с пропусканием exp( im ф ). Эти моды обладают одинаковыми фазовыми скоростями, и поэтому их линейная комбинация (1) не может вращаться при распространении. Это также следует из условия вращения (10) при n = n ' = const ( B ₂ = 0).

метрическая функция, Г( x ) – гамма-функция.

Условие вращения для многомодового ГГ-пучка имеет вид:

n — n'

B ₂ =------= const,                        (10)

m - m '

где B 2 /4 – число оборотов, которые совершит пучок (1) с модами (7) в промежутке от z =1 до z = R . Заметим, что в промежутке от z = R ^{- 1} до z =1 ГГ-пучок совершит B ₂/4 оборотов в обратную сторону.

Проекция на ось z линейной плотности орбитального углового момента лазерного пучка (1) с модами (7) на единицу мощности описывается по-прежнему выражением (4). Поэтому, используя условие вращения (10) и выражение для орбитального углового момента (4), можно сформировать лазерный пучок, у которого, например, будет вращаться поперечное распределение интенсивности и будет нулевой орбитальный момент. На рис. 3 показаны распределения интенсивности двухмодового ГГ-пучка с коэффициентами C (0,2) = 1 и C (3,-2) = 1. Такой пучок вращается влево ( B₂= - 0,75) и не обладает орбитальным момен

а                 б                в

Рис. 3. Распределения интенсивности в сечении двухмодового ГГ-пучка, рассчитанные на разных расстояниях z от начальной плоскости:

1,5 м (а), 2 м (б) и 2,5 м (в)

В заключении приведем некоторые экспериментальные данные. При проведении экспериментов использовался бинарный жидко-кристаллический микродисплей CRL Opto SXGA H1 с разрешением 1280 x 1024. На рис. 4 показана бинарная фаза, предназначенная для формирования двухмодового пучка Бесселя формирования светового поля, представляющего собой суперпозицию двух мод Бесселя c номерами C( a ₁, 3)=C( a ₂, -3)=1 ( а ₁=1,4 х 10⁴, а ₂=7 х 10³). Размер сформированной фазы составил 7 x 7 мм.

Рис. 4. Бинарная фазовая картина, сформированная на микродисплее

а                      б                  в

г                          д                       е

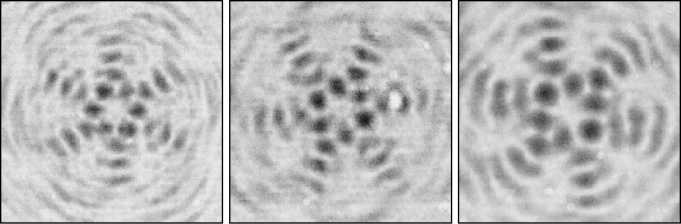
Рис . 5. Картина дифракции вращающегося двухмодового пучка Бесселя на разных расстояниях от микродисплея (а, б, в – эксперимент, г, д, е – теория): z=720 мм (а, г); z=735 мм (б,д); z=765 мм (в, е)

Распределения интенсивности в сечении одного из двух сформированных пучков, измеренные на разных расстояниях от микродисплея с помощью CCD-камеры, показаны на рис. 5.

Работа выполнена при частичной финансовой поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUXO-014-SA-06), а также гранта РФФИ 05-08-50298 и 07-07-97600, и при поддержке «Фонда содействия отечественной науке».