Временное «сжатие» фемтосекундного импульса в фокусе усечённого микроэллипсоида

Ввиду достаточно широкого применения ультракоротких импульсов в различных областях науки и техники множество работ посвящено способам их пространственно-временного преобразования и фокусировки [1, 2]. Так, в работе [3] нами было проведено моделирование FDTD-методом фокусировки двух фемтосекундных лазерных импульсов разной длительности с помощью четырёх микролинз (сфера, полусфера, параболоид, эллипсоид) с эквивалентными параметрами и с учётом частотной дисперсии вещества с помощью классической модели Селлмейера. В ходе работы было показано, что микросфера лучше фокусирует излучение: ширина фокусного пятна по полуспаду интенсивности в плоскости, перпендикулярной плоскости поляризации, составила (0,42 ± 0,04) λ , в плоскости, параллельной плоскости поляризации, – (0,52 ± 0,04) λ [1]. Сфокусированное ею излучение имеет более высокий коэффициент фокусировки и наименьший коэффициент временного уширения. Также было показано, что, несмотря на слабую зависимость дисперсионной кривой для кварца от длины волны в области видимого спектра, результаты фокусировки коротких импульсов микросферой могут приводить к относительной ошибке в 15–28 %, если не учитывать частотную дисперсию вещества.

Из результатов экспериментального анализа оптических свойств кварцевого стекла следует, что общепринятая (трёхпараметрическая) модель Селлмейера применима в диапазоне от 0,21 до 7 мкм [4]. При анализе процессов распространения ультракоротких импульсов длительностью менее 3,5 фс необходимо использовать модель, учитывающую все особенности диэлектрической проницаемости кварцевого стекла. В работе [5] нами были найдены параметры (резонансные длины волн, амплитуды и коэффициенты демпфирования) модели Селлмейера для более точного согласования (среднеквадратическое отклонение 6 %) модельных кривых показателей преломления и поглощения с облаком экспериментальных значений дисперсионных кривых кварцевого стекла.

В данной работе проводится расчёт в рамках лучевой оптики оптического элемента из кварцевого стекла для фокусировки фемтосекундного импульса. С помощью FDTD-метода с учётом дисперсии материала производится моделирование процесса фокусировки ультракороткого импульса с помощью рассчитанного элемента и микросферы. Для учёта дисперсии используются две модели: классическая модель дисперсии Сел-лмейера (КМД) [4] и уточнённая модель дисперсии (УМД) [5]. По результатам моделирования производится сравнение коэффициентов фокусировки и временного уширения световых импульсов.

1. Лучевой расчёт оптического элемента

Рассчитаем поверхность оптического элемента (ДОЭ), фокусирующего параллельный пучок в точку на поверхности. На рис. 1 показан ход лучей. Поверхность имеет вращательную симметрию относительно оси z .

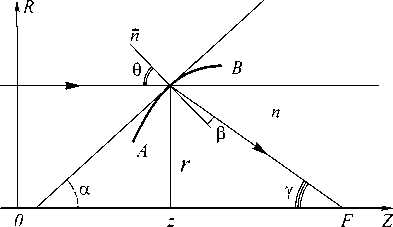
Рис. 1. Схема преломления света поверхностью

Пусть луч, параллельный оси z и отстоящий от неё на расстояние r, падает на преломляющую поверхность AB , преломляется, входит в среду с показателем n и пересекает ось z в точке F (фокус). Из рис. 1 следуют уравнения:

sinθ= nsinβ ,(1)

d r

=tgα,(2)

d z

r

= tgγ , z′= F-z ,(3)

z e = Y+P,

Уравнение (8) можно записать в форме эллипсоида:

п е = -а,

n ² r ² + ( n ² - 1 ) I z' -

z 0 I

n + 1 J

где е, в, а, у - углы падения, преломления, наклона касательной и фокусировки.

Из уравнений (1)–(5) можно получить уравнение для любого параллельного падающего луча, преломляющегося в фокус:

= , 2 ( ^{n -} 1 ) ⁿ n z ⁰ n + 1

.

d r = ( ^ r 2 ^{+ z}'^{2 - nz} ') d z'          nr

Из (6) видно, что при r = 0 производная d r /d z '^^ , т. е. угол а = 90° (вершина оптического элемента). Если лучи на рис. 1 заменить на обратные, то уравнение (6) будет уравнением поверхности r = r ( z' ) или z' = z' ( r ) для коллиматора, т. е. уравнение (6) описывает элемент, который все лучи, исходящие из точки F на оси, преобразует в параллельный пучок лучей вдоль оси z . Чтобы этот элемент работал наоборот, т. е. собирал все параллельные лучи в фокус в точку F на задней поверхности, надо к уравнению (6) добавить условие синфазности всех приходящих в фокус лучей. На рис. 2 показана схема для вывода условия, что все лучи приходят в фокус с одинаковой фазой.

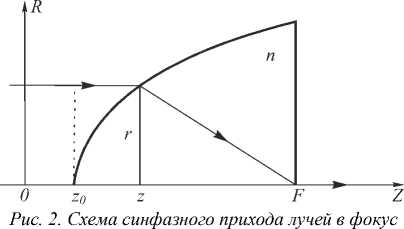
Условие синфазности:

n/r ² + z ^/2 +( Z 0 - z ') = nz 0 , z 0 = F - z ₀,        (7)

где z 0 – начальная координата расположения вершины оптического элемента. Из (7) получим уравнение поверхности:

7 ( n ^- 1 )( z 0 ^- z ) r = ------------- X

n x 7 [(n+1) z+(n- 1) z 0 ]

0 <  z' <  z 0 .

Поверхность (8) обеспечивает синфазность (или одновременность) прихода всех лучей, параллельных оптической оси, в точку фокуса F . Но надо убедиться, что эта поверхность так преломляет лучи, что они действительно приходят в точку F . Можно показать, что решение (8) удовлетворяет уравнению (6), то есть поверхность (8) обеспечивает также нужное преломление падающих на неё лучей, параллельных оптической оси. С помощью замены переменных ^ = r / z' можно решить уравнение (6) при условии, что r ( z 0 ) = 0. При этом получим решение в виде (8).

Вернёмся к уравнению (6), из которого видно, что при условии r = z'4n1 -1                                   (10)

касательная к поверхности (8) будет параллельна к оптической оси. Из условия (10) можно найти координату z' , при которой расстояние r от оптической оси до поверхности (8) максимально:

^z = ^z 0

1 + V2 n ² - 1 2( n + 1)

Из уравнений (10) и (11) можно найти синус «крайнего» луча, приходящего в фокус F , то есть найти числовую апертуру эллипсоида (9):

NA = n sin Y_max = У n ² - 1 .                      (12)

max

Из (12) следует, что дифракционный предел (минимальное значение), который может достигнуть величина диаметра фокального пятна (по полуспаду интенсивности), сформированного эллипсоидом (9) в среде с показателем преломления n = 1,5, равен

FWHM = 0,51 — = 0,46 % .               (13)

NA

На рис. 3 представлен оптический элемент, рассчитанный по формуле (9) при n = 1,4967 и

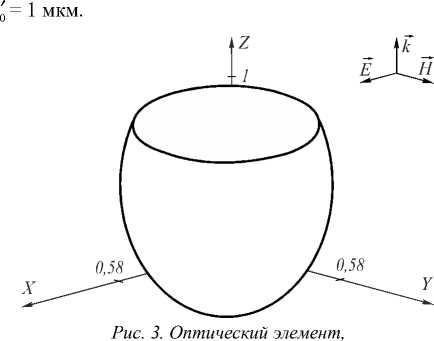
рассчитанный по формуле (9)

2. Моделирование фокусировки

С учётом того, что микросфера показала лучший результат по фокусировке фемтосекундного излучения [3], проведём сравнение рассчитанного элемента с соответствующей ему микросферой радиусом 0,58 мкм. Материалом линз будем считать кварцевое стекло. С помощью FDTD-метода с учётом дисперсии проведём моделирование распространения ультракороткого Гауссова импульса длительностью по полу-

спаду интенсивности 1,24 фс [3] через рассчитанный элемент (рис. 3):

( x )   .( y )

ψ ( x , y , z = 0, τ ) = rect     rect ×

( a J    ( b J

[ (T-0,5 • c• t Y1 . Г 2n )              (14)

x exp < -1I ^ sin I — t I, И    td    J I ^ J где a = b = 1,6 мкм – размер стороны квадрата, ограничивающего плоскую волну в начальной плоскости;

τ = сt, мкм; с – скорость света, мкм/с; t – время, с; ts – длительность импульса, с; td – ширина импульса, мкм. Несущая длина волны импульса равна 0,532 мкм. Плоскость поляризации импульса совпадает с плоскостью XZ (отлична от нуля только компонента Ex).

В ходе моделирования воспользуемся сначала классической моделью Селлмейера для описания дисперсии кварцевого стекла [4] (табл. 1), а потом уточнённой моделью [5] (табл. 2):

^t(^)--+ :? i?^^^^ ■

где ε ∞ – диэлектрическая проницаемость на высоких частотах; λ – длина волны, мкм; λ m – резонансная длина волны, мкм; A m – величина резонанса; δ Sm – коэффициент демпфирования, мкм.

Табл. 1. Параметры классической модели Селлмейера для кварцевого стекла

m	A m	λ m	δ Sm
1	0,69616630	0,068404300	0
2	0,40794260	0,11624140	0
3	0,89747940	9,8961610	0
ε∞ =1

Табл. 2. Параметры уточнённой модели Селлмейера для кварцевого стекла

m	Δε m, мкм	λ m, мкм	η m, мкм
1	0,60616630	0,067404300	0,028
2	0,16	0,0983	0,017
3	0,440794260	0,11624140	0,01
4	0,59747940	9,04616108	0,35
5	0,00520045	12,6739082	0,05
6	0,75	22,1243678	1,8
ε ∞ =1

Моделирование производилось при следующих расстояниях между узлами сетки отсчётов: h_x = 0,02 мкм, h_y = 0,02 мкм, h_z = 0,015 мкм , h _τ = 0,005 мкм. На рис. 4 показано временное распределение интенсивности падающего импульса и соответствующий ему спектр.

На рис. 5 представлены распределения интенсивности импульса в момент фокусировки для каждой из вышеописанных микролинз. Выходные плоскости микролинз обозначены вертикальной линией.

В табл. 3–5 приведены размеры фокусного пятна по полуспаду интенсивности FHWM и глубина фокуса по полуспаду интенсивности DOF.

Из табл. 3, 5 видно, что вне зависимости от используемой модели диэлектрической проницаемости диа- метр фокусного пятна по полуспаду интенсивности, полученного с помощью фокусировки ультракороткого импульса рассчитанным ДОЭ, не меняется и в плоскости, параллельной плоскости поляризации, составляет (0,53 ± 0,04) λ, а в плоскости, перпендикулярной плоскости поляризации, составляет (0,38 ± 0,04) λ. Сфера и эллипсоид (9) одинаково хорошо фокусируют излучение, но сфера формирует более круглое фокусное пятно.

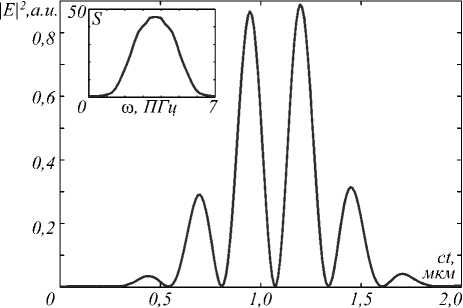
Рис. 4. Временное распределение интенсивности в точке (x, y, z) = (0, 0, 0,2) мкм и спектр для входящего импульса длительностью 1,24 фс

Табл. 3. Диаметр фокусного пятна по полуспаду интенсивности FHWM вдоль x (вдоль линии начальной поляризации) в λ

	Эллипсоид (15)	Сфера
КМД	0,53	0,45
УМД	0,53	0,45

Табл. 4. Диаметр фокусного пятна по полуспаду интенсивности FHWM вдоль y, которая перпендикулярна начальной плоскости поляризации в λ

	Эллипсоид (15)	Сфера
КМД	0,38	0,38
УМД	0,38	0,38

Табл. 5. Глубина фокуса по полуспаду интенсивности DOF вдоль z в λ

	Эллипсоид (15)	Сфера
КМД	0,2	0,11
УМД	0,17	0,11

Из рис. 5 видно, что эллипсоид (9) и сфера фокусируют излучение вблизи своей поверхности.

На рис. 6 представлены графики временного распределения интенсивности в точке фокусировки.

В работе рассчитаны коэффициенты фокусировки, временного уширения и сужения спектра по следующим формулам:

k f = I f / I in ,                                           (16)

где k f – коэффициент фокусировки; I f – величина максимальной интенсивности сфокусированного излучения, I in – величина максимальной интенсивности падающего излучения, a.u, a.u. – произвольные единицы;

k t = t out / t in ,                                                  (17)

где kt – коэффициент временного уширения; tin – длительность входящего импульса по полуспаду интен- сивности, фс; tout – длительность выходящего импульса по полуспаду интенсивности, фс,

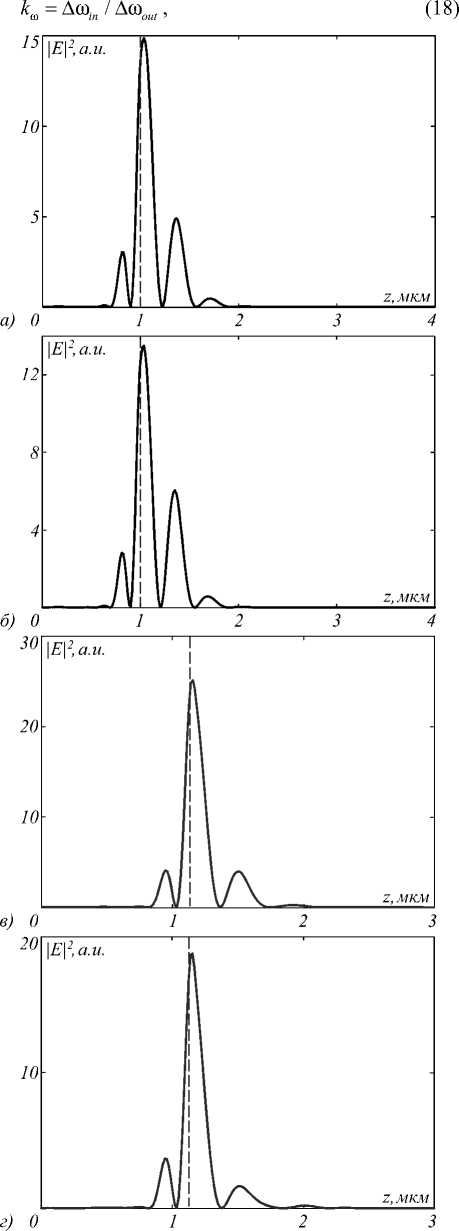
Рис. 5. Распределение интенсивности вдоль оптической оси для импульса длительностью по полуспаду интенсивности 1,24 фс в момент фокусировки:

рассчитанным усечённым эллипсоидом (КМД) (а); рассчитанным усечённым эллипсоидом (УМД) (б); сферой (КМД) (в); сферой (УМД) (г)

где k _ω – коэффициент сужения спектра; Δω _in – ширина спектра входящего излучения, ПГц; Δω _out – ширина спектра выходящего излучения, ПГц.

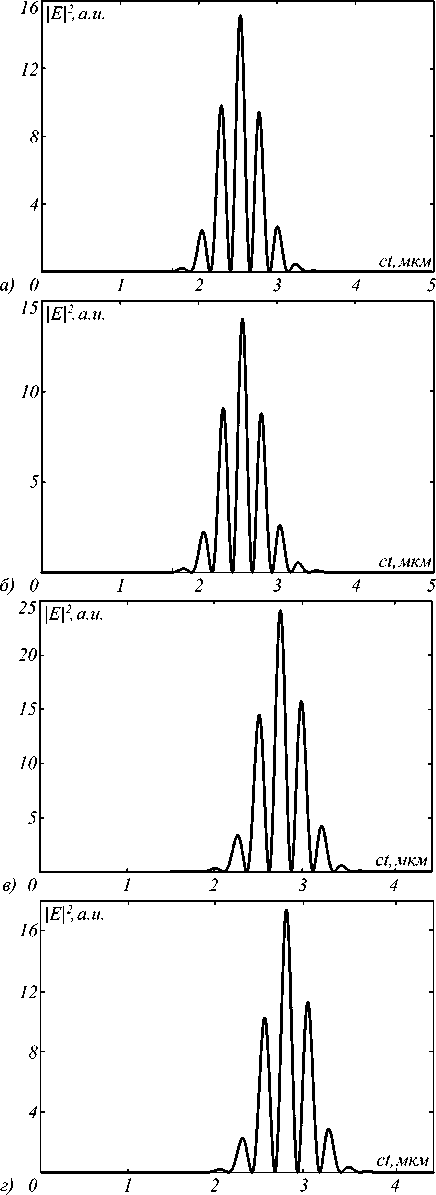
Рис. 6. Временное распределение интенсивности в точке фокусировки для импульса длительностью по полуспаду интенсивности 1,24 фс, сфокусированного: рассчитанным усечённым эллипсоидом (КМД) (а); рассчитанным усечённым эллипсоидом (УМД) (б);

сферой (КМД) (в); сферой (УМД) (г)

В табл. 6–8 приведены коэффициенты фокусировки, временного уширения и сужения спектра.

Табл. 6. Коэффициент фокусировки

	Эллипсоид (9)	Сфера
КМД	18,16	28,88
УМД	16,84	20,91

Табл. 7. Коэффициент временного уширения

	Эллипсоид (9)	Сфера
КМД	0,95	0,84
УМД	0,96	0,87

Табл. 8. Коэффициент сужения спектра

	Эллипсоид (9)	Сфера
КМД	1,57	1,49
УМД	1,61	1,42

Из табл. 7, 8 видно, что из-за продольной дифракции в пространстве все импульсы при распространении уширяются и, соответственно, их спектр сужается. При этом коэффициент временного уширения во всех рассмотренных случаях составляет величину меньшую единицы, т.е. в фокусе импульс на 5 – 10 % сжимается во времени. Коэффициенты сужения спектра также достаточно близки друг к другу и составляют около 1,5.

Из сравнения результатов моделирования фокусировки ультракроткого импульса двумя микролинзами: эллипсоидом и сферой – видно, что использование КМД вместо УМД приводит к погрешности порядка 3 % для эллипсоида и 14,9 % для сферы (если пренебречь сдвигом из-за запаздывания излучения при использовании УМД).

Заключение

В работе в рамках лучевой оптики получено уравнение эллипсоида (9), который все параллельные лучи фокусирует в точку на оптической оси; с помощью моделирования FDTD-методом, учитывающим дисперсию вещества, фокусировки фемтосекундного импульса (длительностью 1,24 фс и несущей длиной волны λ =532 нм) с помощью кварцевого усечённого микроэллипсоида с меньшим диаметром сечения 1,16 мкм показано, что эллипсоид даёт эллиптическое фокусное пятно с меньшим диаметром FWHM = 0,38 λ , хотя геометрическая оптика предсказывает минимальный диаметр фокуса, равный FWHM = 0,46 λ (уравнение (13)). Причина преодоления дифракционного предела в том, что фокус формируется не в среде, а на границе двух сред, и в его формирование вносят вклад поверхностные волны, конструктивная интерференция которых приводит к уменьшению диаметра фокуса.

Проведено численное сравнение фокусировки фемтосекундного импульса рассчитанным эллип- соидом и микросферой с одинаковым диаметром 1,16 мкм. Оказалось, что параметры фокусных пятен в обоих случаях очень близки, но эллипсоид тем превосходит сферу, что параметры фокуса у него в 5 раз менее чувствительны к изменению модели дисперсии.

Работа выполнена при поддержке Министерства образования и науки РФ, грантов РФФИ (14-0797039, 14-07-31218, 13-07-97008) и гранта Президента РФ (МК-4816.2014.2).