Временной анализ упругопластических конечномерных диссипативных систем при нестационарных воздействиях

Временной анализ реакции конечномерных систем с внутренним трением представляет исключительно сложную и трудоемкую задачу, особенно в тех случаях, когда требуется проводить учет пластических деформаций в элементах конструкций при нестационарных воздействиях. Поэтому аналитические решения в подобных задачах крайне редки и связаны с упрощающими предпосылками. Упрощения относятся либо к выбору расчетных динамических моделей с числом степеней свободы не более одного-двух [1, 2], либо к выбору модели упруговязкого сопротивления, обычно соответствующей классическому пропорциональному (однородному) демпфированию [3].

В [4] изложены основные положения теории временного анализа, основанной на разработанных методах анализа матричных линейных и нелинейных уравнений. Эта теория обладает достаточно широкой областью приложений. Объектами исследования являются конечномерные (дискретные) диссипативные системы (ДДС). Учет внутреннего трения проводится на базе линейной модели вязкого сопротивления. Разрешающие уравнения как упругой, так и неупругой реакции строятся в замкнутом виде через интеграл Дюамеля, причем в задачах колебаний ДДС с нелинейной восстанавливающей силой закон деформирования подчинятся идеально упругопластической диаграмме Прандтля. Важно подчеркнуть, что эффективность подхода не зависит ни от типа демпфирования (однородное, неоднородное), ни от характера внешнего воздействия и соответствующего ему режима колебаний.

Теоретические основы

Общая идея подхода состоит в использовании теории промежуточных состояний (в рамках теории пластического течения). Весь процесс неупругого анализа реакции разбит на такие интервалы, внутри которых динамические параметры системы неизменны. Переход из одного интервала в другой происходит при скачкообразном изменении параметров жесткости в критических временных точках tb соответствующих открытию или закрытию шарниров текучести. Поэтому на каж дом отдельном интервале используется схема упругого решения, а при переходе через критические точки решения на смежных интервалах стыкуются посредством начальных условий, обеспечивающих непрерывность движения упругопластической диссипативной системы. В результате весь неупругий процесс представляется рядом последовательно изменяющихся квазиупругих решений.

Условие равновесия динамической квазиуп-ругой системы на произвольном интервале времени г е [z„ z^-i], где t_b t_M - время перехода в промежуточные состояния, выражается матричным уравнением движения

MY(t) + С Y(0 + Д^)Г(0 = Р(?),        (1)

где

P(t) =-R0(t,) + R* (t,) + P(t).

Здесь: М= diag (т_ь ..., m_n\ С = С^т, ^(Z,) = К^)¹ - матрицы инерции, демпфирования и жесткости соответственно; 7?oto> R (ti) - векторы составляющих восстанавливающих сил (предельных значений и остаточных усилий); Y(t), P^f) - векторы искомых перемещений и заданной внешней нагрузки (все обозначения приняты в соответствии с работой [4]).

Уравнения реакции системы на интервале t е [Zj, Z_i+1] (z = 0, 1,...) имеют вид:

Y^ = ^Zk(z), F(z) = ^S^Z,(z), (2) 4=14=1

Z,(Z) = Ol(z-zJ^4-S;F0+F0] +

+А (0 [-^o Vi) + R* 0-)] + Vk кЛ > где Uk=-Ui = M(Sk - Sj) (/=1,2;/* к), Ф^) = es*‘;

Fo, Fo - векторы начальных условий (перемещений и скоростей);

A(z)=J®I(z-r)dr;(4)

Vk 0) = JФ* V - ^У (г) dr .(5)

Уравнения реакции (2), (3) обобщают интеграл Дюамеля на область физически нелинейных систем, позволяя на квазиупругом интервале определять значения перемещений и скоростей узлов упругопластической конструкции при произвольной нагрузке. Матрицы Sk (к = 1,2) суть корни характеристического уравнения движения собственных форм (матричного квадратного уравнения): MSk + CSk + KQb = 0 (z = О, 1,...), которое вытекает из однородного дифференциального уравнения, соответствующего (1).

Технический анализ проблемы

Проблема реализации разрешающих уравнений (2), (3) требует построения аналитических зависимостей для интегралов (4), (5). Это наиболее предпочтительный вариант, хотя не исключена возможность использования численных процедур. В любом случае сложности временного анализа переносятся на область технической реализации задачи. Как показали исследования, формализация интегралов (4), (5) на базе строгого математического аппарата оказывается чрезвычайно плодотворным шагом, что позволяет задействовать весь технический арсенал методов анализа сложных ДЦС, ориентируя их на современную вычислительную технику и делая доступными для практи ческого применения.

Вычислительная формула интеграла (4) зависит от условий состояния квазиупругой системы [4]. При условии невырожденного состояния (det Sk * 0) интеграл (4) представляется конечной формулой Mf) = (5*^Т)^-1[Ф*^Т(/ - У - £]. В случае вырожденного состояния при полной диссипации системы (det Sk = 0, det Si * 0), интеграл (4) имеет вид функционального ряда

■'.(-)= »I(»)Z(-s.T) 4ти1Г' (6)

Вычислительная формула (6) может быть преобразована к более простому виду, не содержащему матричных функций-сомножителей, что позволит эффективнее осуществлять практический анализ уравнений (2), (3). Покажем это.

Поскольку для фундаментальной матрицы ФХО справедливо разложение в бесконечный ряд по степеням матричного аргумента S^.

р=0

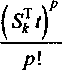
то проведем почленное перемножение элементов ряда в (6). Выполнив группировку слагаемых перед одинаковыми степенями матричных корней Sk, получим скалярные функции ap(t) (р = 0, 1, ...) в виде степенных рядов:

р (-iy(t^q+x-t^^x\t^p-^q (9 + 1)!(р-9)!

в результате чего формула (6) запишется так

AW=f(5j)\(0-           (8)

р=0

Проведем более детальное исследование функции (7).

Вынесем величину 1/(р + 1)! за знак суммы. Замечая, что факториальный множитель, входящий в 17-й член ряда, является биномиальным коэффициентом многочлена (Z - /,) ^1, то есть д+1 _    (р + 1)!

-(9+1)!(р-9)1*

д+1

где С_р+1 - число сочетаний из р + 1 по у + 1, будем иметь

«,(')- ^ 1м "с% (,’*'- <Г)  ■

В развернутой форме записи получим многочлен со степенями t^p~^qtf^+x

--НГ' C^tt? -(-if c^r¹}, где

Cp₊i =c^i -c^x +...+(-i/’"¹ qf+i +(-1/ c^¹.

Далее учтем некоторые свойства биномиальных коэффициентов:

„p-q гр+х-г° -1 A\q-Xrq -n ср+1 - Cp+1 , Cp+1 - Ьр+1 - 1. 2j\ V         °’ g=0

согласно которым 1     Р+1          п

В соответствии с формулой бинома Ньютона имеем д=0

Сопоставив правые части двух последних выражений, приходим к очевидному соотношению ap(t) = (t- tb ^Ир + 1)!. Отсюда, учтя (8), найдем окончательно р=0

t-tr¹ (р + 1)! '

Таким образом, получено аналитическое выражение интеграла (4), обеспечивающее разложение МО в одинарный ряд с более простой (по сравнению с (6)) структурой входящих в него членов. С технической точки зрения организация вычислений ряда (9) намного проще, нежели для ряда (6), поскольку при программировании задачи для многочленов вида (I - t,)^¹ гораздо удобнее использовать схему вложенных умножений.

Вычисление интеграла (5) связано с характером внешнего воздействия. Рассмотрим действие кратковременной нагрузки по синусоидальному закону P(t) = sinQ t-P₀, где 0 = Ея11_а, Е - единичная матрица, t_a - время действия нагрузки; Р_о - вектор амплитуд внешних сил. Тогда из (5)

Vk (0 = 4 04, 4 (О = М (' ~r)sm(^e7)^dT ■ <¹⁰)

Техника вычисления интеграла Ito изложена в [4] и сводится к исследованию непрерывного уравнения Сильвестра (t g [1„ 1,+J (/ = 0,1,...))

№^I^=F№,       (11)

правая часть которого определяется выражением

Fto = Ф^М/ДО/ sinOz, + 0 cos01J -- [Sj sin01 + 9 cos01].

Здесь матрицы St (£ = 1, 2) являются постоянными величинами на интервале времени t е [1,, 1,+1]. Для скалярной матрицы 9 из (11) вытекает обычное матричное линейное уравнение

[(s/)²+e²w=7t(0[№^T)² + е²]= Fto, из которого непосредственно следует

Ito = К«Л² + 6²]^-1^0 = Fto [С4^Т)² + О²]^-1.

Пример расчета

Рассмотрим пример упругопластических колебаний 3-этажного каркасного здания с металлическими колоннами и железобетонными перекрытиями, находящегося под действием кратковременной нагрузки большой интенсивности синусоидальной формы P(f) = sin ^ETttlt^Po, где t_a = 0,8 с -продолжительность импульсной нагрузки. Вектор амплитуд динамических сил равен Р_о = [250, 30, 170]^т (кН). Расчетная схема здания имеет вид сдвиговой модели (рис. 1), согласно которой ригели считаются абсолютно твердыми (заключающими в себе массы этажей) и жестко соединенными с невесомыми колоннами. Поперечные сечения колонн (сталь С255) нижнего этажа - сквозные, верхних этажей - сплошные.

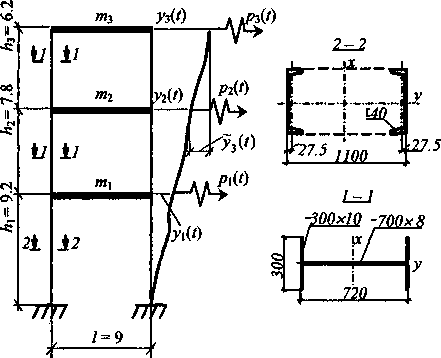
Рис. 1. Расчетная схема 3-этажного каркасного здания

На основе инерционных и жесткостных характеристик конструкции сформированы следующие матрицы: М= diag (2,97,2,97,2,1) (кНс²/см),

К =

289,96

-99,62

-99,62

297,97

-198,36

-198,36

198,36

(кН/см),

93,88 -32,04

С = -32,04 95,17

-64,16

•10"2 (кНс/см).

0    -64,16

64,97

Демпфирование является неоднородным и учитывается по модели [4]: С = (КТ + ТКУ2, где Т= diag (fi, 1_Ъ 1₃); 1, = ^a^mj г^⁰*⁵, т,, Гц - диагональные элементы матриц Т, М, К; 8 = 0,1 - логарифмический декремент колебаний.

Значения предельно упругих перемещений концов колонн по этажам здания составили Уо= [1,57, 1,72, 1,09]т см. Вследствие высокой скорости деформирования (ё = З-Ю”3 > Ю"4 с-1), реакция системы на интервале 1 е [0, 1О] вычислялась с учетом изменения прочностных свойств материала. Превышение динамического предела текучести [2] над статическим обусловило возрастание предельно упругих перемещений на активном участке нагружения на 5 %.

Численная реализация упругопластической задачи проводилась в универсальной математической системе MatLab. Шаг временного анализа был принят М = 0,01 с. При поиске критических временных точек минимальный шаг доходил до 10^-7 с. Основные этапы временного анализа по вычислению параметров неупругой реакции приведены в табл. 1-3.

Табл. 1 содержит информацию о времени образования и закрытия пластических шарниров в несущих элементах этажей здания, включая повторную текучесть и разгрузку в колоннах второго этажа (см. второй полуцикл диаграммы деформирования на рис. 2).

Таблица 1

№№ этажей	Начало текучести 1„ с		Начало разгрузки 1»с
здания	1-й п/ц	2-й п/ц	1-й п/ц	2-й п/ц
1	0,4235	0	0,8548	0
2	0,6039	2,1113	1,1570	2,1174
3	0	0	0	0

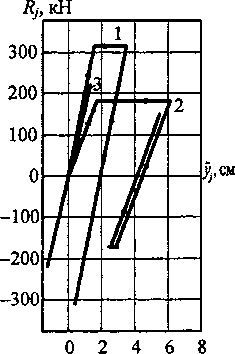
Рис. 2. Диаграммы деформирования «восстанавливающая сила - относительное перемещение» конструктивных элементов этажей здания

В табл. 2 представлены значения максимальных относительных перемещений каждого этажа здания (вектор У^ ), остаточных относительных и абсолютных перемещений (векторы У* =У_тах-Уо, У*), накопленных в процессе реагирования системы.

В табл. 3 дана некоторая информация о промежуточных состояниях квазиупругой системы на интервалах t е [/,, /_/+1] (переходы из одного промежуточного состояния в другое происходят в моменты времени ^).

На диаграмме «восстанавливающая сила -относительное перемещение» (рис. 2) изображены жесткости этажей конструкции в упругопластической стадии. Причем диаграмма деформирования 2-го этажа состоит из двух полуциклов, каждый из которых содержит площадку текучести. Первый полуцикл диаграммы построен при динамическом предельно упругом перемещении, равном Уог = 1,05-1,72 = 1,806 см, так как начало текучести (/2 = 0,6039 с) по времени оказалось в активной зоне нагружения. Высота площадки текучести соответствует предельному значению восстанавливающей силы Т?02 = 179,9 кН. Второй полуцикл построен при Т?02 = -171,3 кН и статическом пре дельно упругом перемещении у02 = 1,72 см, поскольку начало текучести по времени (/5 = 2,1113 с) относится к этапу свободных колебаний здания. Вследствие необратимых деформаций колебания этажей происходят со смещением относительно первоначального недеформированного положения здания.

На рис. 3 приведены осциллограммы параметров неупругой реакции здания при нестационарном процессе от импульсного воздействия. Колебания второго этажа совершаются с учетом гистерезисного характера диаграммы деформирования (рис. 3 а). Движение этажа на отрезке времени t е [0, 1,492 с] соответствует первому полуциклу диаграммы. Асимптоты a_b by на графиках фиксируют уровень остаточных смещений (абсолютный и относительный), устанавливающий новое положение равновесия этажа при его колебаниях. Начиная с момента времени /₆, происходит понижение этого уровня на величину 0,00653 см (асимптоты а₂, Ь^ вследствие разгрузки и смены знака пластических деформаций при реализации второго полуцикла диаграммы деформирования (/ > 1,492 с). При t = /₃ абсолютные перемещения второго (и третьего) этажа возрастают на величину

Таблица 2

№№ . этажей . здания	Наибольшие перемещения Imax ’ СМ	Относительные и абсолютные остаточные перемещения в к-х полуциклах диаграмм деформирования
		У*, см			У*, см
		1-й п/ц	2-й п/ц	за оба п/ц	1-й п/ц	2-й п/ц	за оба п/ц
1	3,5662	1,9177	0	1,9177	1,9177	0	1,9177
2	6,2685	4,4626	-0,0065	4,4560	6,3803	-0,0065	6,3737
3	< 1,1445	0	0	0	6,3803	-0,0065	6,3737

Таблица 3

Параметры реакции		Время Ь (с) начала открытия или закрытия пластических шарниров
	j	/,=0,4235	/2 =0,6039	ta =0,8000	/3 =0,8548	/4 =1,1570	/5=2,1113	/6=2,1174
f = fe)’	1 2	1,6485 0,0778	2,4953 1,8060	3,4223 3,5129	3,4877 4,1001	2,4418 6,1826	1,3901 2,7425	1,4108 2,7360
см	3	0,4853	0,5805	0,6604	0,4130	0,5814	-0,3579	-0,3580
МЛ),	1 2	5,2486 7,3361	5,1660 9,1227	2,3943 10,1631	0 11,1249	-3,2352 0	3,9375 -2,1533	2,8848 0,0036
см/с	3	-0,5868	2,3307	-3,6806	-4,9809	3,6847	0,4419	-0,4571
	1 2	1,6485 1,7263	2,4953 4,3013	3,4223 6,9352	3,4877 7,5878	2,4418 8,6244	1,3901 4,1326	1,4108 4,1468
см	3	2,2116	4,8818	7,5955	8,0008	9,2058	3,7747	3,7889
^0 = (йу)’	1 2	5,2486 12,5847	5,1660 14,2887	2,3943 12,5574	0 11,1249	-3,2352 -3,2352	3,9375 1,7842	2,8848 2,8883
см/с	3	11,9979	16,6194	8,8768	6,1440	0,4495	2,2261	2,4312
	1	313,778	133,869	133,869	-179,909	0	171,341	0
Дз,кН	2	0	179,909	179,909	179,909	0	-171,341	0
	3	0	0	0	0	0	0	0
	1	0	0	0	365,012	-79,536	-79,536	-78,885
R*, кН	2	0	0	0	0	444,548	444,548	443,897
	3	0	0	0	0	0	0	0

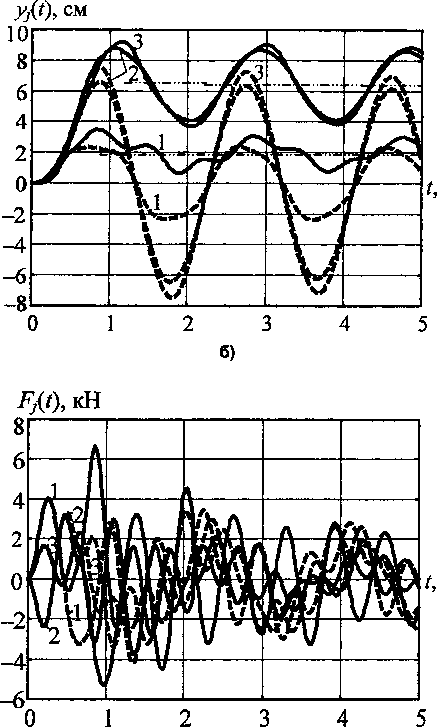
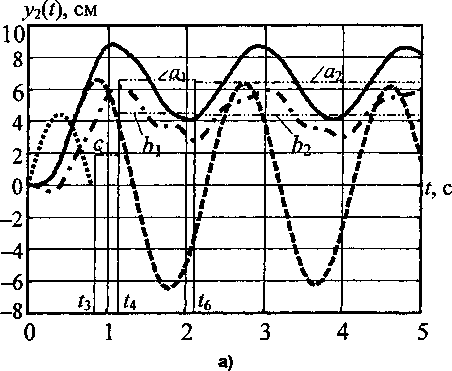
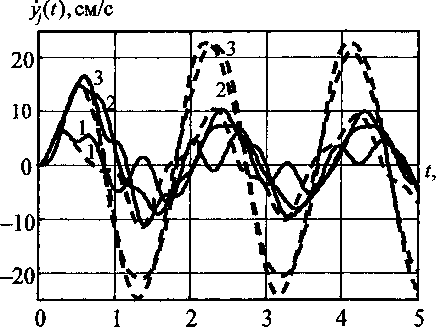
Рис. 3. Осциллограммы параметров упругопластической реакции каркасного здания (цифры на графиках - номера этажей; пунктир - упругая реакция здания): а - перемещений 2-го этажа (сплошная линия - абсолютные; штрих-пунктир - относительные; точки - статические перемещения); б - перемещений всех этажей; в - скоростей; г - диссипативных сил

1,9177 см. Это вызвано развитием и последующим накоплением пластических деформаций в концевых сечениях колонн первого этажа (асимптота ci).

Более общую картину упругопластической работы этажей конструкции иллюстрируют осциллограммы перемещений (рис. 36), скоростей (рис. Зв) и сил внутреннего трения (рис. Зг).

Экстремальные пики на осциллограмме диссипативных сил образуются в моменты времени, соответствующие появлению текучести. При этом наибольшие значения силы (положительная F₂ = 6,65 кН при t = 0,86 с и отрицательная F_x = -5,26 кН при t = 0,98 с) приходятся на интервал текучести t е [t₂, Q, когда происходит рост пластических деформаций в колоннах второго этажа.

Таким образом, полученные результаты свидетельствуют о высокой эффективности метода временного анализа в задаче колебаний конструк ций с учетом вязких и пластических свойств материала при нестационарных воздействиях.