Временной отклик четырёхволнового преобразователя излучения на тепловой нелинейности

Важнейшей характеристикой любого четырёхволнового преобразователя излучения является соответствие между комплексными амплитудами падающей (сигнальной) и преобразованной (объектной) волн. Знание такого соответствия позволяет решить вопрос о целесообразности применения четырёхволновых преобразователей в системах нелинейной адаптивной оптики, в системах обработки и преобразования изображения и т. д. [1].

Линеаризация уравнений, описывающих четырёхволновое взаимодействие, в приближении заданного поля по волнам накачки, относительно комплексных амплитуд сигнальной ( А ₃) и объектной ( А ₄) волн позволяет установить интегральную связь между временными зависимостями этих волн t

A 4 ( t ) = J X ( t , t l ) A 3 * ( t l ) d t l - 0

Здесь x ( t , 1 1 ) — временной отклик.

При четырёхволновом взаимодействии в тонких нелинейных средах (фотохромных, фоторефрактив-ных, средах с тепловой, резонансной нелинейностями) выражение для временного отклика хорошо описывается одной или суммой экспоненциальных функций [2-5]. В частности, ширина временного отклика четырёхволнового преобразователя излучения на тепловой нелинейности, на резонансной нелинейности с учётом диффузии частиц зависит от пространственных частот взаимодействующих волн. В [4] для среды с резонансной нелинейностью показано, что учёт толщины нелинейного слоя оказывает существенное влияние на характеристики временного отклика.

Представляет несомненный интерес исследование временного отклика четырёхволнового преобразователя на тепловой нелинейности с учётом толщины нелинейного слоя, изучение временной динамики качества обращения волнового фронта таким преобразователем излучения.

Уравнение (1) дополняется нестационарным уравнением теплопроводности

— = ЛV²5 Т + — AA * .

d t

c P ^v

Здесь A = ^ A j , A и A ₂ - комплексные ампли- j = 1

туды волн накачки, δ T – изменение температуры, обусловленное выделением тепла при поглощении излучения, c_p - теплоёмкость, Л - температуропроводность, v - плотность вещества, n 0 - среднее зна-

® n, чение показателя преломления, к =---, а - коэф- c

фициент поглощения.

В приближении заданного поля по первой волне накачки, при учёте решётки, возникающей при интерференции первой волны накачки и сигнальной волны, распределение интенсивности можно записать следующим образом

I = AA •= 1 0 + A₁A ; + A ; A 3 ,                     (3)

где 1 0 = A ₁ A ; .

С учётом (3) изменение температуры среды можно представить в виде суммы быстро (δ T₃₁ ) и медленно (δ T₀ ) меняющихся в зависимости от коор-

динат составляющих

5 Т ( Г, t ) = 5 Т о ( F , t ) + 5 T 31 ( F , t ) + 5 T^ ( F , t ) .

Волновое уравнение (1) распадается на систему уравнений вида

V 2      I , , 2 d n

V + к 1 +--- 5 T_n

I n 0 d T ⁰

V ² + к ² 1 1 + —— 5 T_o

I    n 0 d T ⁰

2k2 dn n0 dT

5 T ₃₁ A 2 .

2 ik а^ A m = 0, m = 1 ^ 3,

2 ik а ^ A ₄ =

1. Вывод выражения для временного отклика

Исходное скалярное волновое уравнение, описывающее вырожденное четырёхволновое взаимодействие to=to+to-to в среде с тепловой нелинейностью, есть [4]

Нестационарное уравнение теплопроводности

распадается на два уравнения

V ² +

7 2 | ।    2 dn k I 1 +---5 T

(    n о d T

J 1

>2ik «IK A + A > 0. (1)

<

^{d5 T} 0 av2xt I ^{a I} 0

----= ЛV 5T +--, dt               cp v d5 T31       2      aA,A3'

-----= ЛV 5 T ₃₁ +--

_ a t                    c p v

.

Пусть волны накачки плоские:

A ( r, t ) = A i,2 ( z , t ) exp ( - iK 2 r ) •

Сигнальную и объектную волны разложим по плоским волнам

X

Aj( r, t )= J A/a z, t) exp (- i j - j) dj

-X

,(6)

j = 3,4, а быстро осциллирующую составляющую температуры – по гармоническим решёткам

5 T_3i ( r, t ) = J 5 T _3i ( к _t , z , t ) exp ( - i к _T p ) d K _T .

-X

Здесь A j ( к j , z , t ) - пространственный спектр j -ой волны, 5 T _3i ( K _T , z , t ) - пространственный спектр тепловой решётки, к j и k_jz - поперечная и продольная составляющие волнового вектора k_j .

В приближении медленно меняющихся амплитуд, с учётом разложения взаимодействующих волн по плоским волнам, а быстро изменяющейся в пространстве составляющей температуры по гармоническим решёткам, от систем уравнений (4), (5) можно перейти к следующим системам уравнений

Граничные условия на изменения температуры записаны при условии неизменности температуры на гранях нелинейного слоя.

Решение первых трёх уравнений системы (7) есть

A ( ^z , t ) = A 10 ( t ) exp ^[- C i ( ^z , t ) ^] ,

A ( z , t ) = A 20 ( t ) exp ^[- C 2 ( z , t ) + C 2 ( 1 , t ) ] ,        (9)

A 3 ( к 3 , z , t ) = A 30 ( к 3 , t ) exp ^[- C 3 ( z , t ) ] ,

„ ( 3 k f| ik dn ,    , где Cj(z, t ) = — 11 ——5T0 (zi, t ) + a kjz 0 In 0d T d z1 .

Сделаем замену , A ₄ ( z , t ) = AA ‘ ( z , t ) exp [- C 4 ( z , t ) ] .

Тогда с учётом (9) при квазиколлинеарной геомет- рии взаимодействующих волн уравнение, описывающее изменение пространственного спектра объ- ектной волны, примет вид

d^ 4 ( K 4 , z , t ) = d z

ik   d n _~(„       ;       4

^- T , ^{5 T} 3i ^(к t , ^z , t ) A 20 ⁽ t ^)x k n d T

x exp { - iz ( k _{2 z} - k _{4 z} ) + C ₂ ( 1 , t ) } .

Из уравнения (10) следует, что временную зависимость пространственного спектра объектной волны на передней грани нелинейной среды можно представить следующим образом

dm+A f i

d z

^k mz

кI ~

— —5 T + a A_m = 0, m = 1 + 3,

0           m,, n о dTJ

d A₄   k f.

i +I i d z k - z (

k d n n ₀ d T

5 To + a IA- =

-                ik ² d n

A4 (к4,z = 0,t) =  ----— A20 (t)exp [C2 (1,t)J x k4zn0 dT

l xf dz5T31 (кT,z,t)exp{-iz(k2z - k4z)} .

k— T n ^{5 T} 31 A ' ; exp ^[- i ( ^k 2 z - ^k 4 z ) ^{z ]} , ^k 4 z n 0 ^{d T}

Используя (8), решение для пространственного спектра быстро меняющейся составляющей температуры представим в виде [6]

d5T   . d25T

⁰ = Л '

d t        d z ²

+ ^ 0 , c p ^v

^{-        2 a}      f^{П m}

5 T 31 ( к T , z , t ) =---A sin I — z C p v 1 m = i    I 1 .

x

i

d5 T , f d²

= Л1

d t       [ d z ²

к T 15 T31 +

x

t f ,410 (t')-A3*0 (к4,t')exp{-®m (t- t')} x

a A 1 A ₃ * exp [- i ( k _{i z} - k _{3 z} ) z J

c p ^v

.

l

J exp [^{- iz} i ( ^k i z ^{- k} 3 z )

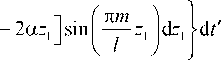
Системы уравнений (7), (8) получены при условии к _T = к 1 - к ₃ = -к ₂ + к ₄. Эти системы уравнений необходимо дополнить граничными условиями:

– на амплитуды взаимодействующих волн:

A 1 ( ^z = 0, t ) = A 10 ( t ) ,

A ( z = 1, t ) = A20 (t ) ,A3 (к3,z = 0,t) = .P. (к3,t) ,■P (к 4, z = 1, t ) = 0;

– на изменение температуры:

5 T0 (z = 0) = 5 T0 (z = 1 ) = 0,5 T3i (z = 0) = 5 T3i (z = 1) = 0.

где tom = Л

n m 1     2— +кт

1 J       ^T

Тогда временной отклик четырёхволнового пре-

образователя на тепловой нелинейности можно за-

писать следующим образом х ( ^к , t , t i ) = ,4 10 ( t i )- A 20 ( t ) ^x x exp ^[ C 2 ( 1 , t ) ^]X i ( к , t - t i ) .

m ²

X

Здесь X i ( к , t - 1 1 ) = X 0 E— m = 1

/ ,4m I i к I I в

- 1 exp ---- - 1

( )      ( 2 k J

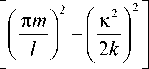
x

( - 1 ) m exp

^^^^^^»

i к ² l

^^^^^^B

X —

n m

2 k

2 a l

^^^^^^B

l

L   i к ²

+ 2a +--

2 k

- exp 'к. ( t - t i

) ] , (14)

X0 =

2 in²k a dn n 0 c p v l ³ d T

Выражение (14) записано в параксиальном при-

ближении

k

V

= k -

5kJ7

при распространении волн

накачки навстречу друг другу строго вдоль оси Z ( ^к₄| = |^кз| = |^к t| = ^к ) .

Выражение (13) с учётом (14) устанавливает однозначную связь между временными зависимостями пространственных спектров объектной и сигнальной волн, позволяет проанализировать изменение качества обращения волнового фронта во времени.

Как и для четырёхволнового преобразователя излучения, в тонком нелинейном слое [2] с ростом пространственной частоты ширина временного отклика уменьшается. При фиксированных параметрах нелинейной среды увеличение частоты ( ® ) взаимодействующих волн приводит к росту скорости уменьшения ширины временного отклика.

Для анализа зависимости ширины временного отклика от толщины рассмотрим четырёхволновое взаимодействие излучения с длиной волны X = 10,6 мкм в нелинейной среде CCl ₄, для которой d n / d T = 5,4 - 10 ^{- 4} К X n ₀ = 1,46, a = 9 см ^{- 1}, Л c p v = 1,03 - 10 ^{- 3}Джх ( смхсхК ) ¹ [7]. С увеличением толщины нелинейной среды ширина временного отклика, монотонно возрастая, выходит на постоянное значение (рис. 2). Величина этого постоянного значения, значение толщины нелинейной среды, при которой происходит выход на постоянное значение, с увеличением пространственной частоты объект-

2. Обсуждение результатов

Численный анализ временного отклика четырёхволнового преобразователя излучения проводился при условии независимости от времени амплитуд волн накачки. При фиксированном значении пространственной частоты к с ростом ( t - t₁ ) модуль временного отклика монотонно убывает. В качестве количественной характеристики временного отклика может выступать ширина временного отклика ( A t ) , определяемая из выражения

| X 1 ( к t ^- t =^A t )| = 2 |xi ( к t ^- t 1 = 0)|.

Ширина временного отклика характеризует время записи тепловой решетки. На рис. 1 приведена зависимость от пространственной частоты нормиро-

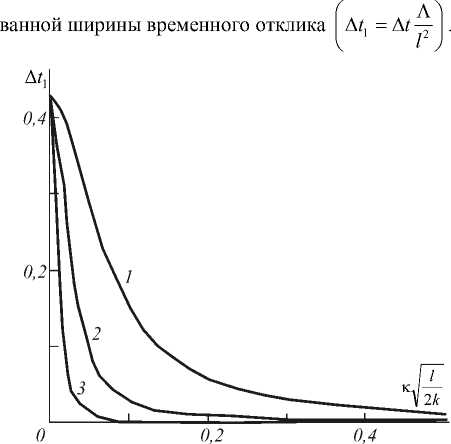
Рис. 1. Зависимость ширины временного отклика от пространственной частоты при kl = 10 (1), 10 (2), 10 (3)

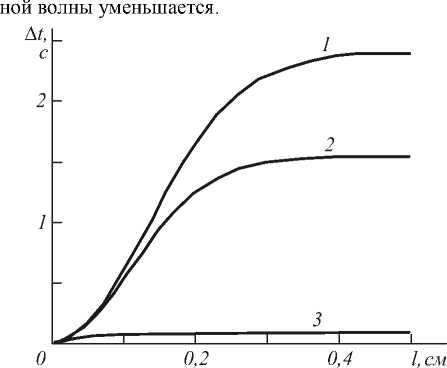
Рис. 2. Зависимость ширины временного отклика от толщины нелинейного слоя при к = 1см - ¹ (1), 10 см - ¹ (2), 100 см - ¹ (3)

Для анализа временной зависимости качества обращения волнового фронта возьмём сигнальную волну от точечного источника, расположенного на передней грани нелинейного слоя, пространственный спектр которой не меняется во времени A ₃₀ ( к , t ₁ ) = 1. Тогда, используя (14), с точностью до постоянного множителя пространственный спектр объектной волны на передней грани нелинейного слоя есть t

^44 (к, z = 0, t) = exp [C2 (l, t)]|X1 (к, t -11)dt1 = m2

да

= X0 exP [ C2 (l, t)]E--- m=1

^m I i ^к I I ( - 1 ) exp - 1

^V V 2 k J

22 n m । I к I ^^^^^^»

l J V 2 k J

( - 1 ) m exp

X-—=-----

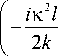
2 a l

-

¹ 1 ^- exp ' ^ - ] '

ращения волнового фронта от толщины слоя с тепловой нелинейностью не зависит.

2 n m I T)

, I            iк I+ 2a +

I        2 k J

V

to ²

m

При анализе качества обращения волнового фронта в качестве нелинейной среды использовался CCl ₄ . На рис. 3 приведены модули пространствен-

ных спектров объектной волны в различные моменты времени. Увеличение пространственной частоты приводит к монотонному уменьшению модуля пространственного спектра объектной волны. Причём с увеличением времени возрастает значение пространственного спектра на низких пространственных частотах, при этом значение пространственного спектра на высоких пространственных частотах не меняется.

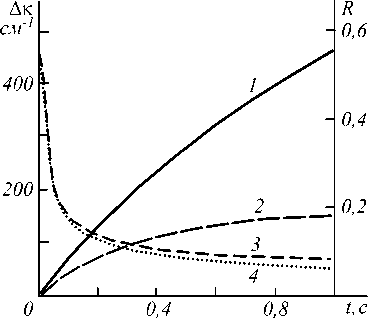
Рис. 4. Временная зависимость коэффициента отражения (1, 2) и полуширины полосы пространственных частот (3, 4) при l=0,1 см (1, 3), l=0,05 см (2, 4)

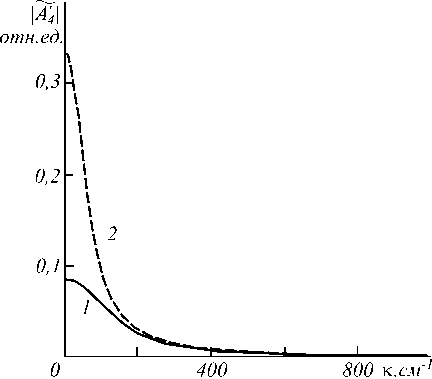
Рис. 3. Пространственный спектр объектной волны в моменты времени t = 0,1c (1), 0,5 c (2)

В качестве количественной характеристики качества обращения волнового фронта может высту-

пать полуширина полосы пространственных частот

( Ак ) , в пределах которой сосредоточена основная

энергия объектной волны [4].

С

I

R=

V

течением времени коэффициент отражения

A 4 ( к = 0, z = 0, t )

AV

А *

A ₃₀

возрастает, достигая ста-

ционарного значения (рис. 4), полуширина полосы пространственных частот уменьшается, также выходя на постоянное (стационарное) значение (рис. 4). Время выхода на стационарное значение существенным образом зависит от толщины нелинейного слоя: для l = 0,05 см оно составляет примерно 0,8 с , а для

l = 0,1 см - около 2 с .

Стационарное значение ширины полосы пространственных частот уменьшается с ростом толщины нелинейного слоя. Уменьшение ширины полосы пространственных частот означает ухудшение качества обращения объектной волны. Причём в начальный момент времени (0< t <0,1 c) качество об-

Заключение