Временной отклик тонкой динамической голограммы в растворе красителя, моделируемом четырехуровневой схемой энергетических уровней

Любое оптическое устройство, в том числе и динамическая голограмма, осуществляет преобразование комплексной амплитуды падающей на нее волны с определенной точностью [1-3]. При использовании динамической голограммы в лазерных измерительных устройствах необходимо установление однозначной связи между пространственной, временной структурой, энергетическими параметрами взаимодействующих волн. Вид этой связи существенным образом зависит от характеристик нелинейной среды, в которой осуществляется запись динамической голограммы.

В настоящей работе для тонкой динамической голограммы в растворе красителя, моделируемого четырехуровневой схемой энергетических уровней, анализируется связь между временными зависимостями комплексных амплитуд предметной и восстановленной волн.

скими волнами, падающими на слой красителя под одинаковыми углами.

N 2

I ^ 12

N 1

1. Модель красителя

Рассмотрим раствор красителя, моделируемого четырехуровневой схемой энергетических уровней, два из которых синглетные, а два других - триплетные (рис.1).

Система кинетических уравнений, описываю-

щая изменение заселенности энергетических уровней, есть [4]

<

dN- = I ^ 12 ^N 1 - ( I ^ 21 ^{+ 8} 21 ⁺ 8 23 ) ^N 2 ,

= 823 N2 -( I C34 + 831 ) N3, dN4

= I O 34 N 3 S 41 N 4 , dt

I ^ 34

I ^ 21

N 4

_ N 1 , + N ₂ + N 3 + N 4 = N .

Здесь N ₁ и N ₂ - заселенности основного и возбужденного синглетных состояний, N ₃ и N ₄ - заселенности триплетных состояний, о _у и 8 j - сечения поглощения (испускания) и вероятности безызлучательных переходов между i и j энергетическими уровнями, I - интенсивность излучения.

2. Запись динамической голограммы

Пусть тонкий слой красителя располагается в плоскости z = 0 . Будем записывать голограмму пло-

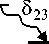
, 831

⁸ 41

Рис.1. Схема энергетических уровней.

N 3

Тогда распределение интенсивности в зависимости от поперечной координаты x будет иметь следующий вид:

I = 1 0 ( 1 + f ■ cos[ Kx + ф ( t ) ] ) . (2)

Здесь 1 ₀ и ф ( t ) - средняя интенсивность и разность фаз волн, записывающих голограмму, K и f -волновое число и глубина модуляции записываемой интерференционной решетки.

Периодическое изменение интенсивности излучения приводит к периодическому изменению заселенности энергетических уровней красителя.

Используя разложение в ряд Фурье, представим заселенности энергетических уровней в виде суммы:

от

N i = £ N j exp ( - ijKx ) , l = 1 ^ 4. (3) j =-от

Будем использовать следующие приближения: 1. пространственное изменение заселенностей происходит по гармоническому закону ( N l 1 >>  N l ₂ >>... ) , 2. глубина модуляции заселенностей небольшая ( N l ₀ >>  N l 1 ) .

С учетом сделанных приближений после подстановки (2), (3) в систему уравнений (1) она распадается на систему двух дифференциальных уравнений, первая из которых совпадает по виду с системой уравнений (1) при замене в ней N_l на N_{l 0} и I на I ₀ , а вторая имеет вид

i

dt ^- I 0 ° 12 ^N 11   ⁽ I 0 ° 21 ^{+ 8} 21 +8 23 ) N 21 +

+F1 ( t ) , d^ = 52з N21 — (I0G34 + 831 ) N31 + F, ( t ) ,     <4)

,   = I0^34N31 — 841N41 — F2 (t), dt

N 11 + N 21 + N 31 + N 41 = 0.

Xi — X9

= -------—------- ‘ . ² ----—--------- x

^{( X} 1 ⁺ p ) ^{( X} 1 ^{+ 8} 41 ) ^{( X} 2 ⁺ p ) ^{( X} 2 ^{+ 8} 41 )

^{( X} 1 ⁺⁸ 41 ^{)( X} 2 ⁺⁸ 41 )  .   .   +Ю4-Х

--+X 1 +X 2 + p +8 41

I 0 ° 34

xi F 10

-

F

^F 20

⁸ 23

^A 0 = { ^(X 1 ⁺ p ^)(X 1 ⁺⁸ 41 ^)(X 2 ^—X 3 ^{) + (X} 2 ⁺ p ^)(X 2 ⁺⁸ 41 ^)x

^X ( ^X 3 ^—X 1 ) ⁺ ( ^X 3 ⁺ p )( ^X 3 ⁺⁸ 41 )( ^X 1 ^—X 2 ) } ^x

Здесь F j ( t ) = j ( t ) exp { ^- z ф ( t ) } , F 10 ( t ) = 2 I 0 f ( \ . ° .. ^—

1 a

^X 1------------------ , ^X 1 = ^M 1 ⁺ M 2 , ,

n ( ^X , + p )( ^X , +6 .1 )                  ³

j = 1

^N 20 ^ 21 ) , F 20 ⁽ t ^{) _} 2 I 0 f ° 34 ^N 30 -

С учетом начальных условий N ₂₀ ( t = 0) = = N 30 ( t = 0) = N 40 < t = 0) = 0, N _m< t = 0) = N для средних значений заселенностей энергетических уровней в случае установившегося процесса ( dNl 0 = 0,   1 = 1 ^ 4) имеем

( dt                J

M . + M₃   M. — M₃ r- a

—¹---² ± i —¹---² V3 — ,

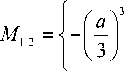
abc

+---±

—

a ² b )

9 3 J

+

N 20 = NI 0 ^ 12 8 41 pP ,

N 30 = NI 0 ^ 12 8 23 8 41 P ,                            (5)

N 40 = NI 02 G 12 G 34 8 23 P .

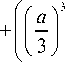
ab c

--+ -

^{6 2} J

Здесь P = { _ 1 ₀ ( o₁₂ + o₂₁ ) + 8₂₁ + 8₂₃ J p 8₄₁ +

2                 )—1

⁺ I 0 ° 12 ⁸ 23 ⁸ 41 ⁺ I 0 ° 12 ° 34 ⁸ 23 } , P = I 0 ° 34 ^{+ 8} 31 ■

Решая систему уравнений (4) с учетом гранич ных условий (N1 1 = 0 I = 1 + 4), получим

N21 = E Cj exp (Xjt), j=1

3 C j ^{exp (}X j t )

N31 = 8 23 E         \ ’ j=1 (X j + p )

м          ^   Cj exp ( ^X jt )

N41 I0°34 8 23 E/л      \/л т V j=1 (Xj + p )(X j + 841 )

A/, где Cj (t) = — J exp {—X/1 - iф(t)} dt1, A0 0

___________________x2 x3___________________

^{( X} 2 ⁺ p ^{)( X} 2 ^{+ 8} 41 ^{)( X} 3 ⁺ P ^{)( X} 3 ^{+ 8} 41 )

A 1 =

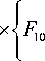
F 20 ^{( X} 2 ^{+ 8} 41 ^{)( X} 3 ^{+ 8} 41 )

⁸ 23 _          I 0 ° 34

+ X 2 +X 3 + p +8 41

______________ X ₃ -X 1 ______________

^{( X} 1 ⁺ p ^{)( X} 1 ⁺⁸ 41 ^{)( X} 3 ⁺ p ^{)( X} 3 ⁺⁸ 41 )

A 2 =

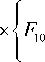
F 20 ^{( X} 1 ⁺⁸ 41 ^{)( X} 3 ^{+ 8} 41 )

⁸ 23 _          I 0 ° 34

+ X 1 +X 3 + p +8 41

a = 10 (g12 + a21 + g34 ) + 821 + 823 + 831 + 841, b = I0°12 (823 + 831 + 841 )+

⁺ I 0 ° 34 ⁽ I 0 ° 21 ^{+ 8} 21 ^{+ 8} 23 ^{+ 8} 41 ) ⁺

+ (I0°21 +821 +823 )(831 +841 ) + I0 °12°34 +831841, c = I0 G34 _°12 (841 + 823 ) + °21841 J +

⁺ I 0 ⁸ 41 ^[ ° 12 ^{( 8} 23 ^{+ 8} 31 ) ⁺ ° 21 ⁸ 31 ⁺ ° 34 ^{( 8} 21 ^{+ 8} 23 ) J ⁺

+8 31 8 41 ( 8 21 +8 23 ) ■

3. Считывание голограммы

Будем считывать голограмму излучением на длине волны, совпадающей с длиной волны излучения, записывающего голограмму. Тогда для рассматриваемой четырехуровневой модели красителя коэффициент поглощения связан с заселенностью основного энергетического уровня соотношением вида a = N,g12 — N2°21 + N3°34                     <7)

С учетом (3) коэффициент поглощения красителя можно представить в виде суммы

X a = E aj exp (—ijKx).                      (8)

j =—»

Подставив выражения для заселенностей энергетических уровней (6), (7) в формулу для коэффициента поглощения (8) при j = 1, получим для установившегося процесса выражение для амплитуды первой гармоники в разложении коэффициента поглощения в ряд:

t 3

^a i

= J Z A exp ( j t — t i ) ) exp ( — i ^ ( t i ) ) dt i ,

о L j = 1

- ^A j (           \ ⁽ ° I2 ° 34 ^{) 8} 23

где A j = -T ^{1    +} ° 21 ) ⁺ h ж \ ⁺

^A o l                ( X j + p )

,       I 0 ^ 12 ^ 34 8 23

( ^X j ⁺ p )( ^ j ⁺⁸ 41 )

Если голограмма тонкая, т.е. изменением интенсивностей волн, записывающих голограмму, на ее толщине можно пренебречь, то амплитуда волны, восстановленной с голограммы ( A d ) , с точностью до постоянного множителя определяется амплитудой первой гармоники в разложении коэффициента поглощения в ряд

A d = ^a i .

Тогда временной отклик тонкой динамической голограммы в растворе красителя, моделируемом четырехуровневой схемой энергетических уровней, будет иметь вид:

х ( t ^- t i ) = Z A j -^e xp { 4- ( t ^- t i ) } .                ⁽¹⁰⁾

j = i

Временной отклик тонкой динамической голограммы представляет сумму трех экспоненциальных функций, весовые коэффициенты ( A j ) и скорость уменьшения во времени ( X j ) которых зависят от интенсивности излучения, записывающего голограмму, параметров красителя.