Время-частотные преобразования с обобщенными маргиналами для анализа нестационарных сигналов в информационно-измерительных системах

В информационно-измерительных и управляющих системах при обработке нестационарных сигналов (в частности, при обработке и анализе речевых сигналов) достаточно широко используются время-частотные преобразования (ВЧП). Существует несколько видов ВЧП. Среди них:

• ■    линейные (кратковременное преобразование Фурье, преобразование Зака (Zak) [1, 2], вре-мя-масштабное (вейвлет-) преобразование [3, 4]);

• ■    билинейные преобразования класса Коэна (L. Cohen) [5, 6] (ВЧП Вигнера—Вилле (Wigner, Ville), спектрограмма [7–10], ВЧП Чои—Вильямса (Choi, Williams) [11, 12], Цхао—Атласа—Макса (Zhao, Atlas, Maks) [13] и положительные ВЧП [14]);

• ■    адаптивные ВЧП [15];

• ■    ряды ВЧП [16], а также афинный, гиперболический и степенной классы ВЧП [17].

ВЧП с точки зрения процедур преобразования систематизированы в [10], но в проведенном ниже анализе ВЧП трактуются в значительной мере с точки зрения его результата — распределения интенсивности сигнала на время-частотной плоскости. В связи с этим вместо ВЧП будет использоваться понятие время-частотного распределения (ВЧР), хотя следует иметь в виду, что реализация ВЧР достигается выполнением соответствующего преобразования.

ВЧП класса Коэна различаются видом ядра и свойствами. Для ВЧП важны свойства маргиналов, которыми традиционно называют значения проинтегрированных ВЧП по одной из двух переменных. Интегралы по оси времени и по оси час- тот (т. е. временной и частотный маргиналы) являются соответственно мощностью сигнала в частотной области (квадратом модуля преобразования Фурье от сигнала) и мощностью сигнала во временнóй области (квадратом модуля текущего значения сигнала). Выполнение этого логического соответствия для ВЧП класса Коэна с ядром φ(θ, τ) зависит от свойства этого ядра, которое определяется соотношением [18]

φ (0, τ ) = φ ( θ , 0) = 1 для всех вещественных θ и τ .

Известно, что когда имеется сигнал с (почти) линейным изменением частоты (СЛИЧ)1), ВЧР должно быть сконцентрировано на линиях в час-тотно-временнóй плоскости, где сосредоточена основная мощность анализируемого сигнала. К сожалению, это далеко не полный ответ на вопрос о том, можно ли, имея априори некоторую информацию относительно сигнала, использовать ее для рационального выбора ВЧР. Следует отметить лишь, что для СЛИЧ было предложено преобразование Радона—Вигнера [19, 20], в котором преобразование Радона используется в области ВЧР Вигнера—Вилле. В [21, 22] было получено совместное распределение произвольных переменных

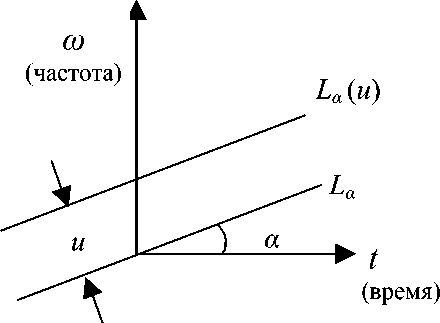
Разметка время-частотной плоскости при определении обобщенных маргиналов

и унитарные преобразования2) времени и частоты.

ВЧР с обобщенными маргиналами упоминалось ранее [16], однако это делалось в совершенно другом контексте, т. е. термин использовался в смысле, отличающемся от анализируемой ниже трактовки время-частотных распределений.

Будем рассматривать ВЧР с обобщенными маргиналами (ВЧР_ОМ), у которых формирование маргиналов отличается от процедуры получения обычных временнóго и частотного маргиналов. Чтобы понять, что представляют такие обобщенные маргиналы, следует обратиться к вращаемому преобразованию Фурье Fа с углом а [23, 24], которое определяется поворотом время-частотной плоскости3). Когда угол а = п/2, Fa равно преобразованию Фурье (ПФ) F, т. е. вращаемое преобразование Фурье (ВПФ) с а = п/2 сигнала являет- ся его ПФ. Когда а = 0, Fa — преобразование идентичности, т. е ВПФ с а = 0 равно самому сигналу. Теперь определяем следующее свойство обобщенного маргинала. Пусть P(t,ю) — это ПФ сигнала s(t) и пусть La означает прямую линию на время-частотной плоскости, проходящую через начало с углом а (см. рисунок).

Пусть L _a ( и ) представляет член семейства всех линий параллельных к L _a (это семейство параметризовано величиной и — расстоянием L _a ( и ) от L _a ).

P ( t, to ) называют ВЧП с обобщенными маргиналами, если линейные интегралы от P ( t, to ) вдоль линий L _{a i} ( и ) ( к = 1, 2,..., N) являются квадратами модуля ВПФ с углами а + п /2 ( к = 1, 2,..., N) сигнала s соответственно. Это выражается соотношением

J P ( t , x )d x = |^ _к + , /2 s ) ( и )², к = 1,2,..., N . (1) Ч ^{( и} )

Соотношение (1), являющееся отражением свойства ВПР с ОМ, в более упрощенной форме может быть представлено в виде выражения

J P ( t , x )d x = |^ + п /2 s ) ², к = 1,2,... Ч

, N .

Нетрудно проверить, что когда а 1 = 0, а ₂ = п /2 и N= 2, то обобщенные маргиналы являются обычными маргиналами. Можно отметить также, что углы а к могут быть выбраны близкими к углу в представлении СЛИЧ на частотно-временнóй плоскости.

Рассмотрим ВЧР при ядре φ ( θ,τ ) в таком преобразовании Коэна, которое является ВЧР_ОМ, т. е. имеет обобщенные маргиналы. Можно показать, что ВЧП с ядром φ ( θ,τ ) в классе преобразований Коэна является ВЧП с обобщенными маргиналами по (1) тогда и только тогда, если ядро φ ( θ,τ ) равно единице на линиях, которые перпендикулярны к L _{a k} , к =1, 2,..., N и проходят через начало. Согласно сформулированному условию наличия у ВЧП обобщенных маргиналов таким свойством обладает преобразование Вигнера— Вилле. Однако это преобразование является единственным из класса Коэна, для которого выполняетя условие, определяющее наличие ОМ.

Анализ показывает, что ВЧР_ОМ обладают хорошими свойства как ВЧР Вигнера—Вилле, так и других билинейных преобразований. Кроме того, ВЧР_ОМ проявляют более высокую устойчивость (робастность) к искажениям сигнала, которые вносятся присутствием аддитивного шума.

БИЛИНЕЙНЫЕ ВРЕМЯ-ЧАСТОТНЫЕ РАСПРЕДЕЛЕНИЯ С ОБОБЩЕННЫМИ МАРГИНАЛАМИ

Анализ билинейных ВЧР_ОМ существенно использует ВПФ, поэтому вначале целесообразно рассмотреть его метод и свойства.

• ■    ВПФ основано на использовании традиционного преобразования Фурье и применении вращения время-частотной плоскости. Для любого а результат применения вращаемого преобразования Фурье F выражением

(Fa$)(и) = а (с углом а) к сигналу $ определяется

/ 1— j ctg ^а e ⁽ “ , ) c ^{tg а} _х

2π t2

х| $ ( t ) e ^{2 g} e ^{( -} jut cosec ^{а )} d t , если а не является числом, кратным п;

s(u),   если а является числом, кратным 2п;

$(-и), если а+п является числом, кратным 2п, где u — аргумент (частотный) ВПФ, примененного к сигналу s. Для ВПФ справедлив ряд простых соотношений, непосредственно вытекающих из (2). Так, F2nπ — это преобразование идентичности; (F(2n+1)π s)(t) = s(–t); Fπ /2 — эквивалентно традиционному ПФ. Кроме того, ВПФ имеет свойство суммирования углов ("свойство вращения") [23]: F+в= = Fa Fв .

• ■    Показано, что вращение ВЧР Вигнера— Вилле дает этот же вид ВЧР [20, 23]. Так, вращение на угол а в частотной плоскости распределения (3) Вигнера—Вилле P W ( t,ω ) сигнала $ ( t ) соответствует связи (4) новых координат t, со с исходными t , ω :

P w ( t , о ) = J $ I t + 2 I $ I t - 2 e - ^o d T ; (3) t = t cos a + го sin a ,

• ⁴⁾    В комплекснозначном выражении вращаемого преобразования Фурье ( F _a $ )( и ) значение квадратного корня берется с угловым аргументом из интервала [- л /2, + п /2], т. е в форме так называемого основного значения комплексной величины.

  о = - 1 sin a + ю cos a .

  
  
  
  

Рассмотрение ( t,ω ) в качестве новых координат соответствует их повороту на - a относительно ( ^f , й ):

Поэтому ВЧР P W ( ^f , co ), являющееся следствием поворота время-частотной плоскости, в которой представлено P W ( t , ω ), выражается соотношением

P W ( ^f , co ) = P W ( t cos a - co sin a , t sin a + co cos a ).

Преобразование правой части этого соотношения с использованием (3) позволяет получить выражение для ВЧР P W ( t, co )

P w ( t, о ) = J ( F a $ ) $ 1 t + 2 ^ $ 1 t - t ^ e-° d T . (5)

Полученное соотношение (5) показывает, что результатом вращения ( P W ( ^f , to )) время-частотного распределения Вигнера—Вилле P W ( t,ω ) сигнала (т. е. сигнала, который получается посредством выполнения вращаемого преобразования Фурье на исходном сигнале s ( t )) является ВЧР Вигнера— Вилле сигнала F _a ( $ ). Заметим, что в форме, подобной соотношению (5) по структуре и логике, Лохманом и Софером (Lohmann, Soffer) [26] показано, что вращение ВЧР Радона—Вигнера является тоже распределением Радона—Вигнера.

• ■ Вращение ВЧР класса Коэна исследовалось Альмейдой (Almeida) [23]. Известно, что один из представителей этого класса — распределение Вигнера—Вилле обладает свойством согласованности обычных маргиналов для а = п /2. Так что из (5) следует соотношение (6), выражающее равенство частотного маргинала у P W ( t, со ) и мощности преобразуемого сигнала ( F _a $ )( ^f )

J P w ( t , of )dcb = |( F a $ )( t )^. (6)

По той же логике справедливо и аналогичное соотношение, выражающее равенство временнóго маргинала у P W ( t, co ) и квадрата спектральной плотности преобразуемого сигнала F _a ( $ ), т. е преобразования Фурье этого сигнала F ( F _a $)(со )

J P w ( t , со )d t =1 F ( F a $ )( со ) =1 ( F a + п /2 $ )( СО ) . (7)

Последнее равенство в (7) основано на упоминавшемся выше свойстве F _{a + п /2} $ = F _{n /2} F _a $ = F F _a $.

УСЛОВИЯ, ОБЕСПЕЧИВАЮЩИЕ СВОЙСТВО ОБОБЩЕННЫХ МАРГИНАЛОВ

Наиболее широкое разнообразие ВЧР порождается преобразованиями, принадлежащими классу Коэна. При определенных условиях эти ВЧР могут иметь обобщенные маргиналы и обладать свойством, характерным для ВЧР_ОМ, в частности свойством по соотношению (1). Поэтому полезно определить неизбыточные условия, обеспечивающие для ВЧР класса Коэна наличие свойства обобщенного маргинала 5).

Для преобразований класса Коэна время-частотные распределения определяются соотношением [5, 7]

P ( t, o ) =     JJ A (6,t) e " ^{j 6 t -} ' d 6 d r ,

4n где A(θ,τ) — так называемая обобщенная функция двойственности сигнала s(t) с ядром ф(6,т):

A ( 6 , т ) = ф ( 6 , т ) f s | u + - I s * | u - - I e^{j 6 u} d u .

I 2 JI 2 J

ВЧР P ( t , ω ) может быть представлено и в несколько более часто встречающейся форме

P ( t o ) =

= JJJ e" ⁶ — j ™ + ^{j 6 u} ф (. 6т ) s ^ u + 1 | s * ^ u - 1 | d 6 d T d u. (8)

При этом P ( t,ω ) является ВЧР_ОМ тогда (и только тогда), если выполняются условия формулы (9), в которой использованы соотношения, связывающие новые координаты ( t,o> ) при повороте время-частотной плоскости с исходными координатами ( t , ω ). Эти соотношения приведены выше в виде выражений (4) и в следующих за ними двух формулах. Для удобства они повторены в сноске ⁶⁾.

Таким образом, с учетом взаимосвязи ( t , ω ) и ( t, 6 ) ) свойство ВЧР_ОМ, представленное форму -лой (1), может быть преобразовано к виду (9):

J P ( t cos a k - t o sin a k , t sin a k + t o cos a k )d t = = |( F       s )(t o )|², k = 1,2..., N .

«k + n /2

Другими словами, время-частотное распределение P ( t , ω ) является обобщенным маргиналом

• ⁵⁾    Понятие неизбыточных условий использовано здесь в смысле, эквивалентном более формальному, но и более строгому понятию необходимого и достаточного условия.

• 6)

t = t cos a + to sin a ,          t = t cos a - to sin a ,

^

to =- 1 sin a + to cos a ,        to = t sin a + to cos a .

тогда (и только тогда), если оно удовлетворяет соотношению (9).

Если теперь взять один некоторый определенный угол а в (9) и использовать в левой части этого соотношения развернутое выражение ВЧР P ( t , ω ) из (8), то можно получить новую форму для левой части (9):

J P ( t cos a - to sin a , t sin a + to cos a ) dt =

cos α

JJ e - j o т (sin a tg a + cos a ) - jur tg a

,    . x I т I * T i ,

Хф(-тtga,t) sI u + 21 s I u-2 IdT du =

= J e-jЮГф(-т sin a,t cos a) As (-t sin a,t cos a)dT, где As — функция двойственности сигнала s.

Функция A s при вращении время-частотной плоскости имеет свойство преобразования, которое как по структуре, так и по способу получения аналогично преобразованию ВЧР и выражается соотношением⁷⁾

A_s ( -T sin a ,t cos a ) = A      T ,0).

F a + n /2 ^

С учетом этого свойства в качестве продолжения начатого преобразования левой части выражения (9) может быть получено соотношение (которое необходимо для определения условия наличия свойства ВЧР_ОМ)

J P ( t cos a - t o sin a , t sin a + t o cos a )d t =

= JJ e^{j (} “ ^{-t B} ) ^т ф ( - T sin a , t cos a )| ( F _{a +} ^ ₂ s ) ( u )| d u d r .

Таким образом, свойство (существования у ВЧР) обобщенного маргинала в форме выражения:

J P ( t cos a - t o sin a , t sin a + t o cos a )d t =

= ^F a + П /2 s ) o )f,

(т. е. (9) при определенном значении угла) выполняется тогда (и только тогда), если соблюдается следующее соотношение8):

J ej ( u ^{6 ) т}ф (^__т sin a , т cos a )d T = 5 ( u - 6 5 ) .

В свою очередь, это значит, что φ ( –τ sin α , τ cos α )= = 1.

Несмотря на то, что проведенные преобразования проведены для одного определенного угла ВПФ, оно по такой же логике непосредственно обобщается на несколько углов α k для k = 1, 2,…, N . Поэтому полученный результат фактически устанавливает, что ВЧР P ( t , ω ) (8) класса Коэна с ядром ϕ ( θ , τ ) является ВЧР_ОМ с углами { α k }, k = 1, 2,…, N в соответствии с (9) только при условии

φ ( –τ sin α , τ cos α ) = 1, ∀ τ и для k = 1, 2,…, N.

Другими словами, φ = 1 на линиях, которые перпендикулярны линиям L _{α k} , проходящим через начало (см. рисунок).

ОБЩАЯ ХАРАКТЕРИСТИКА ВРЕМЯ-ЧАСТОТНЫХ РАСПРЕДЕЛЕНИЙ С ОБОБЩЕННЫМИ МАРГИНАЛАМИ

Из найденного условия следует, что для любого набора углов к ВЧР_ОМ относится одно из основных — распределение Вигнера—Вилле, поскольку у него ядро φ = 1 для всех θ и τ . Кроме того, используя полученное условие для ВЧР_ОМ, можно видоизменить известные ядра (лежащие в основе ВЧР класса Коэна) таким образом, чтобы соответствующие им распределения стали время-час-тотными распределениями с обобщенными маргиналами. Примерами такого видоизменения служит соответствие ряда ядер (Рихачека (Rihaczek), Пейджа (Page), Чои—Вильямса, sinc-ядра) их модифицированным формам [5, 11, 28], приведенным в таблице. Эти формы ядер порождают ВЧР_ОМ, также относящиеся к классу Коэна.

Проводившееся предварительное изучение время-частотных преобразований некоторых моделей сигналов (включая СЛИЧ, которые очень показательны с точки зрения оценки чистоты ВЧР и отсутствия элементов интерференции) показало, что ВЧР_ОМ имеют лучшие характеристики, чем соответствующие ВЧР класса Коэна с обычными маргиналами. Лучшей становится и защищенность ВЧР при анализе сигнала с сопутствующим шумом, т. е. повышается так называемая робастность ВЧР. Такое улучшение более выражено, когда берется не слишком мало углов, набор которых входит в условие формирования ВЧР_ОМ. Улучшение ВЧР получается при формировании модифицированного ядра с использованием 4–5 значений углов, равномерно распределенных в интервале 0, π /2.

Увеличение набора углов, входящего в условие для ВЧР_ОМ, ведет к усложнению ядра и увеличивает вычислительную нагрузку при определении ВЧР, однако компьютерная реализация практически полностью снимает это незначительное затруднение.

ЗАКЛЮЧЕНИЕ

Время-частотные преобразования (ВЧП) используются при обработке нестационарных сигналов в прикладных исследованиях, связанных с информационно-измерительными и управляющими системами. Метод ВЧП продуктивен с точки зрения возможности получения динамического спектра измерительных сигналов, облегчающего анализ и интерпретацию изучаемых процессов или верификацию необходимой частотной структуры управляющих сигналов при их целевом моделировании.

Модификация формы ядер ( р ( 6 , т ) ^ф ( 6 , т )), приводящая к ВЧР_ОМ класса Коэна

Название	Вид ядра ϕ ( θ , τ )	Модифицированная форма ядра р ( 6 , т ) с углами a k , к = 1, 2,^, N
Рихачека Пейджа Вильямса sinc	e 0.5 jθτ e 0.5 θ|τ| -θ 2 τ 2 / σ e   τ σ sin ( a θτ ) a θτ	e [0.5 j ∏ k N = 1 ( θ cos ak + τ sin ak )] e 0.5 j [ ∏ k N = 1| θ cos ak + τ sin ak |][ ∏ k N = 1( θ cos ak + τ sin ak )] e ( - 1/ σ ) ∏ k N = 1( θ cos ak + τ sin ak )2 sin[ a ∏ k N = 1 ( θ cos α k + τ sin α k )] a ∏ k N = 1( θ cos α k + τ sin α k )

К наболее исследованным относится группа ВЧП класса Коэна с типовой структурой, основанной на интегральном преобразовании сигнала с ядром (функцией двух переменных). Ядро определяет свойства ВЧП, а наложение определенных условий на ядро позволяет получить полезные свойства ВЧП [18]. Среди них свойство согласованности маргиналов (величин ВЧП, проинтегрированных по одной из переменных — времени или частоте), которое дает возможность интерпретации результата преобразования сигнала как его (вероятностное) время-частотное распределение (ВЧР).

Нередко при использовании ВЧР для сигналов с быстро меняющимся спектральным составом возникают осложнения, обусловленные появлением в этих условиях так называемых элементов интерференции — вкраплений в картину ВЧР, затрудняющих интерпретацию динамического спектра. Использовавшийся ранее способ преодоления этого недостатка был основан на простейших видах изменения формы ядра преобразования и не давал эффективных результатов.

Новым подходом, ведущим к улучшению качественных характеристик ВЧР, является использование концепции обобщенных маргиналов время-частотного преобразования. В отличие от традиционного понятия временнóго и частотного маргиналов ВЧР класса Коэна обобщенный маргинал (ОМ) формируется вне частотного или временнóго измерения, т. к. интегрирование, определяющее ОМ, осуществляется по одной из осей вращаемой время-частотной плоскости. Предложено условие, определяющее наличие обобщенных маргиналов; это условие выражается с помощью сравнительно новой концепции вращаемого преобразования Фурье (ВПФ). В связи с этим приведена характеристика ВПФ, его свойства и некоторые процедуры, необходимые при получении условий, которые определяют существование ОМ у ВЧР.

Для распределений класса Коэна показана форма модификации ядра, необходимая для обеспечения у него определенного числа обобщенных маргиналов. Использование время-частотных преобразований с таким модифицированным ядром существенно улучшает разрешающую способность при анализе динамического частотного спектра нестационарного сигнала в ИИС. Использование описанного метода при анализе сигналов с сопутствующим аддитивным шумом облегчает корректную интерпретацию результата анализа измерительных данных при обработке нестационарных сигналов.