Вскрытие модуляционных параметров радиосигналов с неизвестной структурой

При создании средств, предназначенных для радиоконтроля, реализации адаптивных методов обработок сигналов, радиоразведки и ряда других специальных задач возникает необходимость разработки методов вскрытия модуляционных параметров радиосигналов с неизвестной структурой, способов приема сообщений в условиях структурной и параметрической неопределенности и т.д.

Обобщенной структурной схемой современных средств радиоконтроля, радиомониторинга и средств адаптивной обработки сигналов может быть представлена в следующей виде:

Рис.1. Обобщенная структура комплекса радиомониторинга, радиоконтроля и средств адаптивной обработки сигналов

Блок антенных устройств используется для пеленгации источников излучения и формирования обзора пространства. Блок линейных приемников обеспечивает сканирование частотного диапазона, гетеродинирование сигнала, ампли- тудное, фазовое или синхронное детектирование. Аналого-цифровой преобразователь обеспечивает ввод первичной информации в ЭВМ, которая в свою очередь обеспечивает визуализацию, документирование, хранение, интерактивную и автоматизированную обработку данных, управление блоком приемников и антенных систем.

Можно выделить пять основных этапов обработки при решении задачи индивидуального распознавания источников сигналов в современных системах передачи дискретных сообщений:

• 1.    Поиск и обнаружение излучения (сигналов) в условиях параметрической и структурной неопределенности;

• 2.    Оценка типовых параметров излучения (несущая частота, тактовые частоты, период следования информационных посылок, параметры синхронизации, пеленгация и т.п.);

• 3.    Слепая идентификация и выравнивание канала распространения радиоволн;

• 4.    Идентификация (классификация) вида цифровой модуляции и определение параметров модуляции;

• 5.    Индивидуальное распознавание радиоизлучения.

Этапы 1 и 2 обеспечивают, как правило, достаточный набор признаков для классификации систем передачи. Подходы и методы решения подобных задач достаточно хорошо известны на сегодняшний день [1-3].

Этапы 3 и 4 обеспечивают возможность демодуляции принимаемых сигналов и, с одной стороны, позволяют уточнить параметры, определяемые на первых двух этапах, и соответственно обеспечивают классификацию до типа, с другой стороны, демодуляция сообщения позволяет сформировать не только систему индивидуальных признаков средства передачи, но и потенциально классифицировать пользователя системы передачи.

В целом этапы обработки 3-4 являются необходимым условием для перехода к решению задачи собственно индивидуального распознавания.

Построение процедуры автоматического распознавания с точки зрения теории не вызывает каких-либо трудностей, если определены индивидуальные демаскирующие признаки систем передачи. Однако задачи слепой идентификации по-прежнему являются областью интенсивных теоретических исследований. Основные направления развития систем радиоконтроля и адаптивных устройств обработки сигналов связаны с автоматизацией процедур классификации и распознавания радиоизлучений, возможностью доступа к принятой информации, увеличение точности определения координат источников радиоизлучений, работающих в широком диапазоне частот, в условиях многолучевого распространения и сложной помеховой ситуации.

Решение этих задач осложняется высокой степенью структурной и параметрической неопределенности принимаемых сигналов, а также невозможностью использования техники испытательных сигналов для идентификации и выравнивания канала распространения. В статье рассмотрена задача классификации видов цифровой модуляции и распознавания излучений цифровых систем передачи информации в условиях неизвестных свойств канала распространения радиоволн, структурной и параметрической неопределенности принимаемого сигнала.

Модели сигналов используемых при передаче дискретных сообщений, в условиях структурной и параметрической неопределенности

Модель системы передачи дискретных сообщений может быть представлена в виде следующего выражения (1):

^+x П =+Х

y(t) = J h(t, T) Z sk (t - nT, an W + v(t) , (1) -да n=-x где y(t) - сигнал в приемнике; {an} - последовательность информационных символов алфавита A = {a1,..., ak,..., aM }; sk (t, ak) - канальный сигнал, соответствующий k-му символу; h(T, t) -импульсная характеристика канала связи; v(t) -аддитивная помеха, T – тактовый интервал. В данной модели мы полагаем, что последовательность канальных сигналов {sk (т - nT, an)} содержит помимо информационных также синхросигналы и тестовые (испытательные) последовательности.

Для линейной цифровой модуляции (1) можно преобразовать к виду

П=+да +да

• y ^{( t} ) = Z a n J ^{h ( t , T ) s} 0 ^{( t - nT} ) d ^{T + v ( t} ) ■ (2) п =-да -да

Для каналов с медленными временными замираниями справедливо следующее упрощение:

n =+x +^ю

y^(t ) = Z a n J ht ^{- T ) s} 0 ^{( t - nT} ) d^{T + v ( t} ) . ⁽³⁾ n =-^ —_ro

Далее будем рассматривать модель (3) как основную при разработке методов оптимальной обработки в условиях априорной неопределенности.

В различных случаях априорной параметрической и структурной неопределенности модель канала содержит ряд параметров и/или функций неизвестных на приемной стороне. Неопределенность в рассматриваемом контексте может возникать не только вследствие прохождения сигналов систем передачи через неизвестный искажающий канал, но и в случаях неизвестной структуры и параметров используемых при передаче сигналов, например в системах радиоразведки.

Модель системы передачи, соответствующая случаю параметрической неопределенности, может быть представлена в следующем виде:

п =+да +^

y(t) = Z an Jh(t - тIе)s0 (t - nTl1 )dT + v(t), (4) n=-^ —да где β – вектор неизвестных параметров канала; X - вектор неизвестных параметров системы передачи (канального сигнала).

После дискретизации сигнала в приемнике модель (4) системы передачи дискретных сообщений может быть записана в виде:

п =+ю

y(l) = y(t)t=iT = Zh(n - llв, 1 )an + v(l) ■      (5)

n =-»

В этом выражении последовательность h ( l\ в , X ) , l = 0,..., L известная импульсная характеристика дискретного канала, зависящая от неизвестных X и в векторов неизвестных параметров, L - память канала, v ( l ) - неограниченная последовательность статистически независимых, произвольно «окрашенных» отсчетов шума.

В случае «полной» непараметрической неопределенности относительно импульсной характеристики канала и канального сигнала мы имеем диск- ретно-временную модель системы передачи в виде

L-1

y ^{( l} ) = y ^{( t} )| t = 1T = Z ^{h ( n ) x ( n -} l ) ^{+ v ( l} ) , ⁽⁶⁾

n = 0

где x(l) - неизвестная информационная последовательность, описываемая той или иной статистической моделью содержащая, в том числе синхроимпульсы и тестовые последовательности, h(l) - неизвестная импульсная характе- ристика сквозного дискретного канала системы передачи.

Импульсная характеристика сквозного канала может рассматриваться как детерминированная, так и случайная функция. Модель (6) используется также для описания комплексных дискретновременных систем с одним входом и выходом (SISO). Когда канал в (2) стационарный, выходная последовательность стационарна в дискретном времени. Для линейных, постоянных во времени, частотно зависимых детерминированных каналов (2), когда частота дискретизации выше скорости передачи символов (в целое число M раз) дискретизированный сигнал является циклостационарным, или, что эквивалентно, может быть представлен как вектор стационарной последовательности, лежащий в основе модели с одним входом и множественным выходом (SIMO), где мы складываем в стек M -последовательность входных отсчетов, в течение приема очередного входного символа

L-l n=0

где y ( l ) и h ( n ) M -мерные векторы сигнала в приемнике и импульсной характеристики.

Задачи оптимального приема сигналов в условиях структурной и параметрической неопределенности

В зависимости от поставленной задачи и объема априорной информации мы можем использовать тот или иной подход к задаче разработки алгоритмов оптимального принятия решений или оценивания. Если априори известна хотя бы статистика аддитивных помех, то мы уже можем записать соответствующее правило принятия решений или оценки параметров. При решении задачи обнаружения сигнала, использовании модели сигнала вида (6) и гауссовской аддитивной помехи решающее правило имеет вид [4]:

Л ( у^ , x ) =

⎛ exp ^⎜

⎝

1 zz

² l 1 l 2

⎞

[ y ( l 1 ) ^- s^ |h, x ^)] ■ [ y ( l ₂ ) ^- sfc h x )] ■ B n 1 ( l i , l 2 )

⎠

⎛ exp⎜

⎝

⎞

1 ZZ y ( l 1 ) ■ y^ ) ■ B n ( 1 1 ,1 2 )

^{2 l} 1 ^l 2                                     ⎠

> n ,

L-1

s ( l i |h , x ) = Z h ( n ) x ( n “ l ) , где B - ( 1 1 , 1 2 ) — об- n = 0

ратная ковариационная функция аддитивной помехи; h – импульсная характеристика сквозного канала.

В (8) отношение правдоподобия (слева) сравнивается с порогом η (справа), значение которого определяется выбранным критерием качества обнаружения (критерий Байеса, Неймана-Пирсона, Котельникова или минимакса). Если априори параметры h и x известны, то задача обнаружения сигнала в принципе решена.

Если параметры h и x априори неизвестны, но известны описывающие их плотности вероятности, то решающее правило можно получить интегрированием отношения правдоподобия по неизвестным параметрам. Конечно, столь подробная модель носит чисто гипотетический характер. На практике мы можем предположить справедливость статистической модели в виде статистически независимых дискретных случайных величин только в отношении информационной последовательности x .

Альтернативный подход, называемый адаптивным байесовским подходом предполагает исполь- зование в (8) вместо истинных значений неизвест-ныхпараметровихоценок.Вслучаеиспользования оценок максимального правдоподобия решающее правило (8) можно записать в следующем виде:

Л ( у ) = max Л ( у^ , x ) > n .

h , x

Реально провести перебор по столь большому количеству параметров задача очень сложная. Используя статистическую модель информационного сообщения, задачу перебора можно несколько упростить:

Л ( у ) = max л ( у^ ) = max j Л ( у^ , x ) p ( x ) d x > n . (10)

В качестве квазиоптимального подхода можно предложитьследующуюпроцедуруобнаружения, в которой используется статистическая информация извлеченная из наблюдаемого сигнала.

Предположим, что приемник синхронизирован с передаваемым периодом – задача, которая может быть решена аналогично [5]. Тогда предполагая, что наблюдаемый сигнал имеет также гауссовское распределение, отношение правдоподобия в рамках адаптивного байесовского подхода может быть записано в виде:

. . - ' ЕЕу ( 1 1 ) у ( 1 2 ) [ B ~; 1 ( 1 1 , 1 2 H^{- 1} ( l , 1 2 ) ]

Л ( у ) = e ^{2 1 1 1 2} >n' , (11) где B - ( l 1 , 1 2 ) - оценка обратной функции корреляции дискретизированного сигнала в приемнике, полученная по ансамблю реализаций принятого сигнала, сформированных на различных периодах синхронизации. Если принимаемый сигнал имеет негауссово распределение, то мы можем использовать различного вида аппроксимации распределений наблюдаемого сигнала, используя выборочные моменты более высокого порядка, вплоть до построения выборочных распределений.

Решение задачи идентификации системы передачи дискретных сообщений по регистрируемому сигналу может быть решена на основе совместного анализа импульсной характеристики сквозного канала сквозного канала h и выровненного сигнала x . При этом возможно не только идентификация вида модуляции, структуры передаваемого сообщения, параметров канального сигнала и т.п., но и демодуляция принимаемого сообщения в условиях неизвестного канала и канального сигнала для линейных видов модуляции. Поскольку анализ конкретных алгоритмов в этой части требует более детальных моделей системы, основной упор в данном отчете сделаем на методы слепой обработки сигналов, то есть слепой идентификации сквозного канала и слепой демодуляции и выравнивания.

Слепая идентификации и выравнивание канала распространения

Задачи слепой обработки предполагают широкий класс моделей для описания наблюдаемых сигналов. В случае одномерного входа и векторного выхода модель системы описывается следующим выражением:

+∞

y ( t ) = j h ( t - т ) x ( t ) d T + v ( t ) , (12)

-∞ где y(t) - наблюдаемый (выходной) векторный сигнал со значениями в R M; Ь(г) - неизвестная импульсная характеристика M-мерного канала; v(t) - аддитивная помеха (векторный случайный процесс как правило с независимыми компонентами); х(т) - неизвестный информационный (входной) сигнал.

Различают два основных типа задач слепой обработки сигналов: слепая идентификация канала (оценка неизвестной импульсной харак- теристики или передаточной функции), слепое выравнивание канала (непосредственная оценка информационного сигнала). В обоих случаях для обработки доступны только реализации входного сигнала. В случае слепой идентификации оценка импульсной характеристики может далее использоваться для оценки информационной последовательности, то есть является первым этапом слепого выравнивания, однако в некоторых приложениях важна сама по себе.

Условия слепой идентифицируемости канала зависят от статистических свойств информационной последовательности.

Такеслиинформационнаяпоследовательность описывается моделью стационарного гауссовского временного ряда, то идентификация возможна только для минимально-фазовой системы [6].

Если информационная последовательность описывается периодически коррелированным временным рядом (циклостационарная последовательность), то условие слепой идентификации это отсутствие нулей канала на единичной окружности [7].

Идентификация произвольной импульсной характеристики канала возможна для негауссовских или нестационарных [1] моделей информационной последовательности.

Важным является известный результат [7] о возможности однозначной идентификации систем с одним входом и множественным выходом.

В этом случае возможно использования многочисленных, весьма эффективных алгоритмов однозначной идентификации системы только по одной доступной реализации.

Методы классификации видов цифровой модуляции

Решениезадачиклассификациивидамодуляции предполагает, прежде всего, формирование минимального набора признаков, регистрация которых в отсутствии помех, позволяет однозначно отнести наблюдаемый объект к соответствующему классу.

В настоящее время насчитывается значительное число подходов к решению данной задачи. Основные методы классификации вида цифровой модуляции можно разделить на две основные группы, различающиеся способом построения пространства признаков классификатора:

• -    классификация вида цифровой модуляции по сигнальным созвездиям;

• -    классификация вида цифровой модуляции по сигнальным реализациям.

Классификация вида цифровой модуляции по сигнальным созвездиям используется в основном для классификации линейных видов модуляции без памяти: АМ, ФМ, КАМ.

В данном случае используется как классическая технология принятия статистических решений, так и различные методы распознавания образов – созвездий. Основные методы классификации видов модуляции по сигнальным созвездиям, это:

• -    методы, использующие байесовские правила принятия решений;

• -    метод классификации на основе расстояния Хеллинжера;

• -    метод моментных матриц.

В отличие от классификации по сигнальным созвездиям методы классификации вида цифровой модуляции по сигнальным реализациям позволяют классифицировать не только линейные,но и нелинейные виды модуляции, в том числе и модуляцию частотным сдвигом – МЧС и модуляцию с «прыгающей» частотой.

К данной группе можно отнести арсенал методов спектрального анализа:

• -    анализ спектральных свойств реализаций с использованием классического Фурье-анализа или ограниченного Фурье-анализа (локализованного во времени скользящим окном);

• -    вейвлет-анализ и анализ время-часто-тных распределений;

• -    различные методы статистического анализа, основанные на анализе первых, вторых и высших моментов и моментных функций наблюдаемых реализаций, анализ статистических характеристик пересечения уровней сигнальными траекториями.

При решении задачи классификации методов модуляции исследуется возможность применения нейросетевых технологий [7-9].

Вданнойстатьемырассматриваемалгоритм классификации вида модуляции по сигнальным созвездиям,основанный на минимизации расстояния Кульбака-Лейблера, обобщенный, в том числе и на случай нелинейной модуляции без памяти.

Данный алгоритм эквивалентен алгоритму максимального правдоподобия для больших выборок. Алгоритм позволяет классифицировать различные виды цифровой модуляции. Для случая классификации нелинейной модуляции без памяти анализ данного алгоритма опубликован в [10].

Пусть теперь мы имеем случай нелинейной модуляции без памяти.

Алгоритм примет вид:

C = arg min ⎜ ^j j ⎜

7E ^(zk)log Lzkr))dzkJ, (13) K t1J        p(z k CJ)   J

⎝

где z _k – отсчеты, формирующие k - е созвездие на тактовом интервале. При этом предполагается, что отсчеты шума, взятые на одном тактовом интервале, независимы. Данное предположение кажется естественным для приемников систем радиоконтроля, характеризующихся широкой полосой приема и числом избыточной дискретизации.

В каналах с временным рассеянием после применения «слепой» коррекции канала неизвестными остаются амплитуда и фаза сигнала. Алгоритм максимального правдоподобия можно представить в виде

⎛ ^K

CC j = argmin ^E J^ ^(z k ) log j , а ,Ф K TT ^j

ЖЦ^ k 1 - (14) k C j VP< P ))    )

k = 1

⎝

В случае независимой оценки неизвестных параметров алгоритм имеет вид:

/V

C j

= argmin j ⎜

⎝

K

7 El ^p ( z k )log

^K k =1

p(zk)  dz

p ( z k C j ^aa - ^»)j  ^k

. (15)

⎠

В [11] показано, что при N → ∞ потенциальная помехоустойчивость алгоритма (15) характеризуется расстоянием Кульбака-Лейблера между распределениями p ( z 1 , z 2 ,..., z _K |Cj- ) :

p j = -1 e p ⁽ z k )log (f^zkk)

K и J        P(z k Cj (a dzk. (16)

В таблицах 1-3 показаны расстояния Кульбака-Лейблера для 4-10 отсчетов на тактовый интервал при различных значений отношения сигнал/шум при использовании фазовой модуляции с числом сигнальных позиций 2, 4 и 8 и частотной модуляции с числом сигнальных позиций 2 и 4 для известных амплитуд и фаз сигнала.

Таблица 1а (n = 10)

С/Ш=20дБ	ФМ-2	ФМ-4	ФМ-8	ЧМ-2	ЧМ-4
ФМ-2	0	0,5394	0,8154	7,8401	6,6982
ФМ-4	2,9498	0	0,3886	7,2828	5,9287
ФМ-8	2,4264	0,5872	0	7,0445	5,9544
ЧМ-2	0,6167	1,1166	1,2716	0	0,8042
ЧМ-4	2,2867	1,5103	1,058	1,4428	0

Таблица 1б (n = 8)

С/Ш=20дБ	ФМ-2	ФМ-4	ФМ-8	ЧМ-2	ЧМ-4
ФМ-2	0	0,5394	0,8154	7,867	7,1431
ФМ-4	2,9498	0	0,3886	7,3268	6,3062
ФМ-8	2,4264	0,5872	0	7,0801	6,2791
ЧМ-2	0,5908	1,1004	1,2775	0	0,6897
ЧМ-4	1,7132	1,5001	1,1194	1,0519	0

С/Ш=5дБ	ФМ-2	ФМ-4	ФМ-8	ЧМ-2	ЧМ-4
ФМ-2	0	0,6152	0,6388	2,8678	2,5437
ФМ-4	0,7881	0	0,082	2,6097	2,3931
ФМ-8	0,7776	0,086	0	2,6336	2,4504
ЧМ-2	1,0982	1,4736	1,4600	0	0,8301
ЧМ-4	1,5235	1,4267	1,4156	0,9337	0

Таблица 1в (n = 4)

С/Ш=20дБ	ФМ-2	ФМ-4	ФМ-8	ЧМ-2	ЧМ-4
ФМ-2	0	0,5394	0,8154	7,867	7,1431
ФМ-4	2,9498	0	0.3886	7,3268	6,3062
ФМ-8	2,4264	0,5872	0	7,0801	6,2791
ЧМ-2	0,5908	1,1004	1,2775	0	0,6897
ЧМ-4	1,7132	1,5001	1,1194	1,0519	0

Таблица 2а (n = 10)

С/Ш=10дБ	ФМ-2	ФМ-4	ФМ-8	ЧМ-2	ЧМ-4
ФМ-2	0	0,7114	0,7961	4,1786	3,646
ФМ-4	1,2979	0	0,1888	3,7517	3,3009
ФМ-8	1,2196	0,2041	0	3,7489	3,3864
ЧМ-2	0,9533	1,4772	1,4928	0	0,8789
ЧМ-4	1,7466	1,4372	1,3809	1,1058	0

Таблица 2б (n = 8)

С/Ш=10дБ	ФМ-2	ФМ-4	ФМ-8	ЧМ-2	ЧМ-4
ФМ-2	0	0,7114	0,7961	4,1935	3,8232
ФМ-4	1,2979	0	0,1888	3,7634	3,4464
ФМ-8	1,2196	0,2041	0	3,758	3,5142
ЧМ-2	0,9412	1,4764	1,4953	0	0,7285
ЧМ-4	1,4942	1,481	1,4274	0,857	0

Таблица 2в (n = 4)

С/Ш=10дБ	ФМ-2	ФМ-4	ФМ-8	ЧМ-2	ЧМ-4
ФМ-2	0	0,7114	0,7961	4,2134	4,0845
ФМ-4	1,2979	0	0,1888	3,7792	3,6866
ФМ-8	1,2196	0,2041	0	3,7706	3,7036
ЧМ-2	0,925	1,4748	1,4989	0	0,3844
ЧМ-4	1,0627	1,4903	1,4831	0,4036	0

Таблица 3а (n = 10)

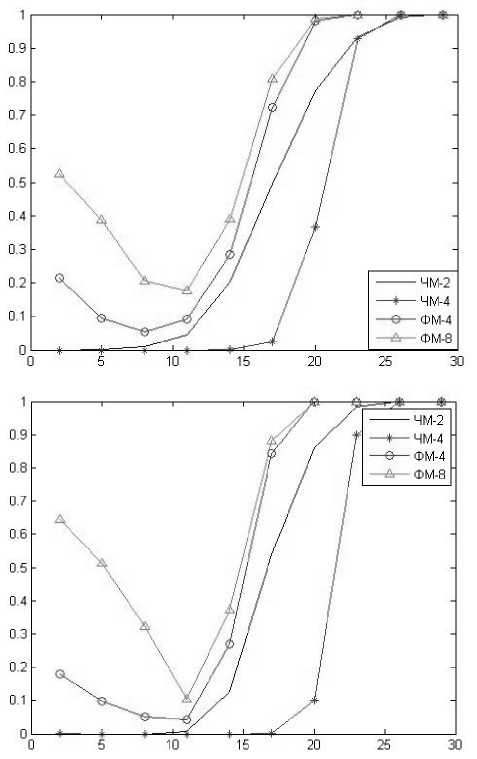
Таблица 3б (n = 8)

С/Ш=5дБ	ФМ-2	ФМ-4	ФМ-8	ЧМ-2	ЧМ-4
ФМ-2	0	0,6152	0,6388	2,8766	2,643
ФМ-4	0,7881	0	0,082	2,6148	2,4699
ФМ-8	0,7776	0.086	0	2.6375	2,5213
ЧМ-2	1,091	1,4736	1,4602	0	0,684
ЧМ-4	1,3935	1,461	1,4463	0,7429	0

Таблица 3в (n = 6)

С/Ш=5дБ	ФМ-2	ФМ-4	ФМ-8	ЧМ-2	ЧМ-4
ФМ-2	0	0,6152	0,6388	2,8835	2,7297
ФМ-4	0,7881	0	0,082	2,6189	2,534
ФМ-8	0,7776	0,086	0	2,6406	2,5762
ЧМ-2	1,0854	1,4737	1,4604	0	0,5262
ЧМ-4	1,2636	1,4765	1,4607	0,5539	0

Из таблиц 1-3 видно, что при изменении числа отсчетов на тактовый интервал расстояние между линейными видами модуляции не изменяется, а расстояние между линейными и нелинейными видами модуляции зависит от количества отсчетов, что приводит к ошибкам в принятия решения в случаях уменьшения расстояния Кульбака-Лей-блера.

Рис. 2. Зависимость вероятности ошибки от дисперсии распределения p ( z 1 , z 2 ,..., z K |C j ) , соответствующей отношению сигнал/шум для четырех видов модуляции при 4 и 10 отчетах на тактовый интервал с отношением сигнал/шум 5дБ

Моделирование производилось для различного числа отсчетов на тактовый интервал ( n = 1; 2; 4; 6; 8; 10).

Распределения p ( z 1 , z 2 ,..., z K |C j ) бралось с различным значением дисперсии, соответствующей отношению сигнал/шум от 3 до 29 дБ при средней мощности сигнала 1 Вт. Шум аддитивный белый гауссовский.

Выводы

Предложенный алгоритм позволяетидентифи-цировать линейныеи нелинейные виды цифровой модуляции. Качество вынесения решения зависит от оптимальности подбора таких параметров как количество отсчетов на тактовый интервал, количество тактовыx интервалов, дисперсия распределения p(z 1 , z2 ’•••’ zK |Cj )’ и конечно, от отношения сигнал/шум в самом канале.

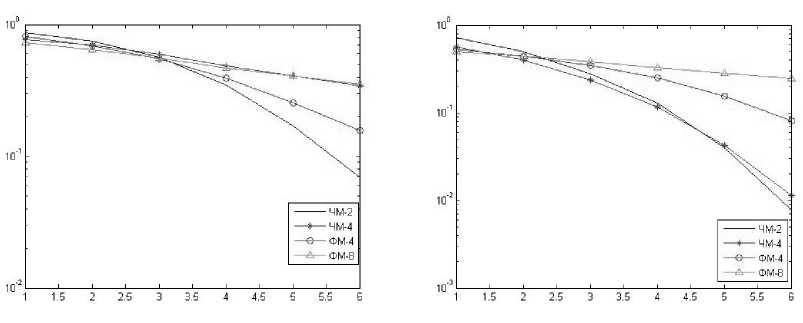
а)                                                  б)

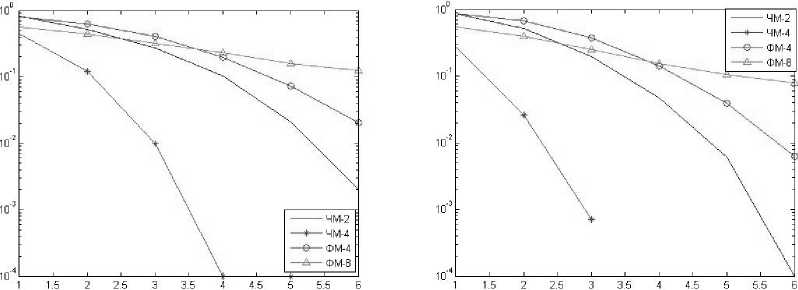
г)

Рис. 3. Зависимость вероятности ошибки от отношения сигнал/шум для четырех видов модуляции при 1, 2, 4 и 8 отчетах на тактовый интервал (а, б, в и г соответственно) при дисперсии, соответствующей 10 дБ