Встраивание цифрового водяного знака в аудиосигнал с применением быстрого преобразования Фурье
Автор: Светов Леонид Андреевич
Журнал: Сетевое научное издание «Системный анализ в науке и образовании» @journal-sanse
Статья в выпуске: 2, 2013 года.
Бесплатный доступ
Статья посвящена вопросам внедрения цифровых водяных знаков в аудиосигналы с применением быстрого преобразования Фурье. В ней рассматриваются методы вычисления быстрого преобразования Фурье, быстрого косинусного преобразования и особенности их программной реализации на языке C++. На основе этих преобразований выбрана методика добавления водяного знака в звуковой сигнал. Статья содержит описание и анализ результатов ее работы.
Цифровой водяной знак, быстрое косинусное преобразование, быстрое преобразование фурье
Короткий адрес: https://sciup.org/14123229
IDR: 14123229
Текст научной статьи Встраивание цифрового водяного знака в аудиосигнал с применением быстрого преобразования Фурье
Задача защиты информации от несанкционированного доступа решалась во все времена на протяжении истории человечества. Уже в древнем мире выделилось два основных направления решения этой задачи, существующие и по сегодняшний день: криптография и стеганография. Целью криптографии является скрытие содержимого сообщений за счет их шифрования. В отличие от этого, при стеганографии скрывается сам факт существования тайного сообщения.
Для защиты персональной информации люди использовали самые разнообразные приемы. Сначала они были довольно примитивными, но с развитием технологий постепенно усложнялись. В век информационных технологий и вычислительной техники развитие стеганографии вышло на принципиально новый этап, который называют компьютерной стеганографией. Скрываемые сообщения стали встраивать в цифровые данные, как правило, мультимедийного характера (изображения, звук, видео).
За последние несколько десятилетий были написаны множество работ в области так называемых цифровых водяных знаков (ЦВЗ). ЦВЗ – специальная метка, незаметно внедряемая в изображение или другой сигнал с целью тем или иным образом контролировать его использование. Это направление стеганографии помогает решать проблемы защиты авторских прав на произведения. Чтобы файл, представляющий собой объект авторского права, не мог быть изменен без ведома автора, чтобы он содержал всю необходимую информацию о правомерном использовании, в него добавляется ЦВЗ. Если произведение подвергается какому-то изменению, то вместе с ним изменяется и водяной знак. Главные требования к ЦВЗ – это его невидимость и устойчивость к внешним воздействиям или помехами (робастность). Эти требования необходимы для того, чтобы усложнить задачу злоумышленнику, стремящемуся уничтожить ЦВЗ.
Существует множество способов добавления ЦВЗ в защищаемые файлы. Когда целью защиты является файл, содержащий оцифрованный аналоговый сигнал, например, звук, то один из возможных подходов в таком случае – применение аддитивных алгоритмов встраивания ЦВЗ. Эти алгоритмы основываются на линейной модификации исходного сигнала, а извлечение ЦВЗ производится корреляционными методами. При этом ЦВЗ обычно складывается с сигналом-контейнером, либо «вплавляется» ( fusion ) в него.
Попытки удаления ЦВЗ из аудиосигнала могут быть основаны на его перекодировании в другие форматы со сжатием или выборочном изменении частот. Смысл в таких действиях имеется, если, конечно, после них контейнер знака похож на исходный вариант, т.е. различия между исходным сигналом и сигналом с удаленным ЦВЗ незаметны [1].
Теоретические основы
В статье рассматривается аддитивный алгоритм внедрения ЦВЗ, основанный на преобразовании Фурье. На сегодняшний день оно является одним из широко распространенных инструментов анализа, применяющимся во всех отраслях науки и техники. В основе преобразования Фурье (ПФ) лежит довольно простая и полезная идея – всякой функции вещественной переменной можно сопоставить другую функцию вещественной переменной, которая будет описывать коэффициенты разложения исходной функции на гармонические колебания с различными частотами. Иными словами, любую функцию вещественной переменной можно представить в виде суммы синусоид с кратными амплитудами, периодами и частотами (рис. 1). Классическое преобразование Фурье задается следующим интегралом [1]:
”
f (u ) = J f (X )e-jxudx.
V 2 n J«
Это преобразование идентифицирует частоты и амплитуды тех комплексных синусоид, на которые разлагается некоторое колебание. Оно определено для функций из пространства L 2 .
Помимо обычного ПФ, также существуют различные его модификации. Одна из них – это дискретное преобразование Фурье. ДПФ широко применяется в алгоритмах цифровой обработки сигналов (его модификации применяются при сжатии звука в формат mp3 , сжатии изображений в формат JPEG и др.), а также в других областях, связанных с анализом частот в дискретном (к примеру, оцифрованном аналоговом) сигнале. ДПФ на входе принимает дискретную функцию, которой ставит в соответствие другую дискретную функцию. Такие функции могут быть получены путем выборки значений из непрерывных функций.
Преобразование Фурье оперирует с комплексными числами, однако в реальных задачах обычно требуется работать с действительными числами. Очевидно, что прямое и обратное преобразования действительного сигнала вернут в итоге этот действительный сигнал. Однако после внесения изменений в частотную область сигнала обратное преобразование может дать комплексные коэффициенты с ненулевой мнимой частью. Эти изменения влекут в общем случае ненулевую мнимую часть преобразования. Таким образом, нам необходимо такое преобразование, которое не выходило бы за рамки действительных чисел.
Обратим внимание на два важных свойства преобразования Фурье: если исходная функция четная, то коэффициенты ее разложения имеют нулевые мнимые части, и выражение идет по косинусам
f (x)=П1I f (t) cos( xt) dt, а если функция нечетная, то разложение идет по синусам, и коэффициенты имеют нулевые действительные части:
f (x) = ЛI f (t)sin (xt) dt.
Эти выражения называется соответственно косинусным и синусным преобразованием. Рассмотрим подробнее дискретное косинусное преобразование (ДКП, Discrete cosine transform , DCT ). Данное преобразование раскладывает сигнал на косинусы с различной амплитудой и частотой. Одна из особенностей ДКП состоит в том, что некоторые локальные участки сигнала можно охарактеризовать небольшим количеством коэффициентов преобразования. Это свойство очень часто используется при разработке методов сжатия данных (например, изображений). Так, ДКП является основой международного стандарта, который используется в алгоритме сжатия изображений с потерями JPEG .
Разделяют несколько разновидностей ДКП [2]. Наиболее распространенные из них – DCT 2 и DCT 3. Это обуславливается тем, что им присуще свойство сохранения основной информации в небольшом числе коэффициентов. Это свойство называют «уплотнением» энергии.
DCT 2: X [k ] = £ x [n ]cosf n(2 n + 1)k 1, k = 0,1,..., N -1, n=0 V 2 N )
1 N -1
DCT 3: X [ k ] = - x [ 0 ] + ^ x [ n ] 2
cos f f k + , k = 0,1,..., N - 1.
IN I 2)) ’
DCT 3 есть не что иное как обратное преобразование для DCT 2 ( Inverse discrete cosine transform , IDCT ).
Итак, прямое одномерное ДКП имеет вид:
X [k ] = a [k ]^ x [n ]cosf П ^n + ^ I, k = 0,1,..., N -1, n=0 V 2 N )
обратное ДКП:
Г 1 N -1 f n ( 2 n + 1 ) k 1 1
x[n] = ^a[k]X[k]cos|—"------~ I» n = 0,1,...,N -1, k=0 V 2 N )
где a [k ] = <
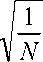
k = 0
k = 1,2,..., N - 1
Данное преобразование можно определить в терминах 2 N –точечного ДПФ. Для этого введем новую последовательность x ' [ m ] длины 2 N , которая получается из исходного сигнала { x [ m ], m = 0,1,..., N - 1 } следующим образом:
x ' [ m ] =
x [m ] 0 < m < N -1x [- m -1] - N < m <-1
Предполагается, что последовательность x ' [ m ] повторяется за пределами интервала - N < n < N - 1 , т.е. является периодической с T = 2 N и симметрична относительно точки m = - 1/2 :
x' [m ] = x' [- m -1] = X' [2 N - m -1]
Если теперь сдвинуть x’ [ m ] на 1/2 вправо, что эквивалентно сдвигу m на 1/2 влево путем объявления новой переменной m ’ = m + 1/2 , то x ’[ m ] = x ’[ m -1/2 ] , что делает последовательность x’[m ] симметричной относительно m ' = 0 . Наглядно такой переход показан на рис. 1. Для простоты в дальнейшем будем понимать под x [ m ] нашу новую последовательность x ' [ m ] .
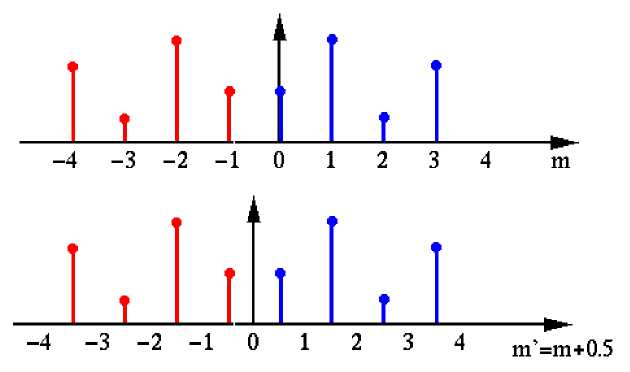
Рис. 1. Отражение сигнала и его сдвиг
ДПФ от этой четно-симметричной последовательности может быть найдена так:
X [n ] =
N - 12
2 N
2 N
2 N
^ - 1
X xm - 2 e
m ’=- N + 12
N - 12
x- - 1 I
X xm - 2 cos
m ’=- N + 12
N - 12
V - 1 I x xm - 2 cos
m ’=- N + 12
- j2nm ' n 2 N
2nm ' n ] j
2 N
—
2 N
N - 12
^ , 1 .
x xm - 2 sin
m ’=- N + 12
2 πm ' n
2 N
^-n | , n = 0,1,...,2 N - 1.
2 N J
Т.к. функция x [ m ]
( 2nm' n ) . ( 2nm' n четная, cosl I и sin I
I 2 N J I 2 N
соответственно четная и нечетная функ-
ции относительно m ’ = 0 или m = - 1/2 , вторая сумма равна нулю. Также следует отметить, что функция X [ n ] действительная и четная, т.е. X [ n ] = X [ - n ] .
Заменяя m ’ на m + 1/2 получаем выражение для ДКП:
X [ n 1 =
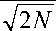
N - 12
E x m '=-N+12
m'-
cosl
2 πm ' n 2 N
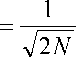
N - 1
E x [ m ]
m =- N
cosl
n ( 2 m + 1 ) n
2 N
22 n — I Г
=^E xm M
I 1 * m =0 \
n ( 2 m + 1 ) n
2 N
n = 0,1,...,2 N - 1.
Т.к. все суммируемые элементы четно симметричны, достаточно использовать только половину точек. Более того, т.к. косинус есть четная функция, X [ n ] = X [ - n ] также четная последовательность с периодом 2 N , получаем:
X [N + n ] = X [N + n - 2 N ] = X [N - n ] = X [n - N ], заметив, что точки X[N + n], n = 0,1,...,N-1 из второй половины совпадают с точками X[N - n] из первой половины, т.е. вторая половина не нужна и поэтому может быть отброшена.
Таким образом, получаем выражение для ДКП:
1 Г2"" N T1 Г 1 Г п (2 m + 1) n ^ N T1 Г 1 Г 1 л 1
X [ n 1 = А ~ E x [ m ] cos | I = E x [ m 1 C [ n , m ], n = 0,1,..., N - 1.
V N m = 0 V 2 N J m = 0
Коэффициент c [ n , m ] есть элемент матрицы косинусного преобразования:
г 1 /2 Г (2 m +1)nn) л cIn, m 1 = J —cos -------— , m, n = 0,1,...,N -1.
L , J V N V 2 N J , , , ,
Все векторы этой матрицы, составленные из ее строк, ортогональны и нормированы кроме первого вектора ( n = 0 ):
N - 1
E c2 [n, m 1 = m =0
2 N r1 2 Г ( 2 m + 1 ) nn )
- — / cos l -------— I = ^
v Nm^ V 2 N J
V 2 n = 0
1 n = 1,2,..., N - 1.
Чтобы сделать ДКП ортонормированным введем дополнительный коэффициент:
a [ n ] =
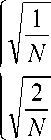
n = 0
n = 1,2,..., N - 1
Тогда выражение для ДКП примет вид:
n - 1 Г ( 2 m + 1 ) nn ^ n - 1
X[n] = a[n]Ex[m]cos| -------— I = a[n]Ex[m]c[n, m], n = 0,1,...,N -1, m=0 V 2 N J m =0
где коэффициенты c [ n , m ] включают в себя a [ n ] и являются элементами матрицы
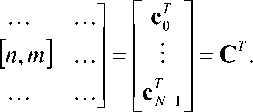
Здесь c f = [ с [ z ,0 ], c [ z ,1 ], ..., c [ z , N - 1 ]] — z —я строка матрицы C . Так как эти строки (векторы) ортогональны, т.е.
( c , c J = c f c j = ^ j
1 i = j
0 i * j
то матрица C ортогональна:
C - 1 = C T , C T C = E .
Таким образом, ДКП может быть записано в матричной форме: X = C T x .
Обратное ДКП имеет вид:
N - 1
N - 1
x [m] = У X [n ]c [m, n ] = У a [n ] X [n ] cosl
(2 m + 1) nn
n = 0
n = 0
2 N
N - 1
= У X[n]c[m, n], m = 0,1,..., N -1, n=0
что в матричном виде выглядит следующим образом:
x = ( C t ) - 1 X = CX .
Как видно из формул, сложность алгоритма, вычисляющего ДКП и обратное ДКП, можно оценить в © ( N 2 ) . Такой сложностью можно пренебречь только при малых значениях N . Решающим фактором применимости таких преобразований является существование быстрого алгоритма, который позволяет снизить вычислительную сложность с © ( N 2 ) операций, которые необходимы для умножения вектора на матрицу.
Задача вычисления ДКП по традиционным формулам довольно проста и не требует дополнительного объяснения. За счет высокой сложности этого алгоритма скорость его работы резко падает при увеличении объема входных данных. Поэтому необходим способ, реализующий эти выражения за меньшее время – быстрое косинусное преобразования (БКП). Подсчет БКП – нетривиальная задача, и она имеет несколько вариантов реализаций. В статье рассматривается методика вычисления БКП, имеющая лучшие оценки скорости выполнения среди остальных алгоритмов [4, 5, 6].
Один из способов вычислить ДКП – взять за основу алгоритм, вычисляющий ДПФ. Такая схема имеет смысл в том случае, когда сложность нахождения ДПФ меньше © ( N 2 ) . В противном случае мы не получим выгоды, т.к. формулы явного ДКП также имеют сложность © ( N 2 ) . Выражения для классического ДПФ нам не подходят из-за большого времени выполнения. Нас интересует алгоритм, требующий меньшего времени. Таковым является быстрое преобразования Фурье или БПФ ( Fast Fourier transform , FFT ). Оно имеет вычислительную сложность © ( N log2 N ) . Соответственно, чтобы быстро выполнить ДКП (сделать быстрое косинусное преобразование или БКП) нужно взять за основу БПФ. Сложность подсчета ДКП имея найденный вектор Фурье-коэффициентов равна © ( N ) . Суммарная сложность подсчета ДКП равна © ( N log2 N ) +© ( N ) =© ( N log2 N ) . Таким образом, используя БПФ для нахождения БКП суммарная сложность нахождения последнего напрямую зависит от сложности БПФ.
В статье рассматривается способ, основанный на алгоритме Кули-Тьюки (Cooley-Tukey algorithm), который использует свойства комплексных корней из единицы. Впрочем, это не единственный метод подсчета БПФ. Так, например, относительно недавно был предложен новый метод вычислений называемый sFFT (Sparse Fast Fourier Transform). Этот алгоритм быстро отыскивает фрагменты с «разреженным» сигналом (sparse signal) и определяет исходную амплитуду в каждом из них. Сигнал разбивается на фрагменты до тех пор, пока не останется разреженный сигнал с единственной амплитудой. А уже там новый алгоритм выявляет её во много раз быстрее классического БПФ [7].
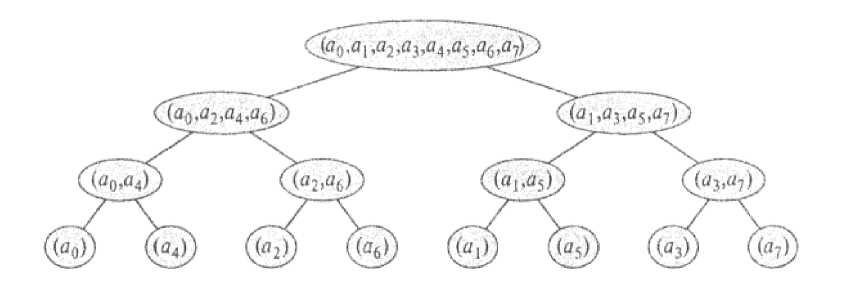
Ниже представлен код процедуры fftRecursive , вычисляющей БПФ [8, 9]. Флаг inverse показывает какое преобразование необходимо вычислить (обратное или прямое).
{ int N=(int)a.size();
if (N==1)
return a;
int N2=N/2;
double f=2*pi/N*(inverse?-1:1);
cmplx w(1),wn(cos(f),sin(f));
vector
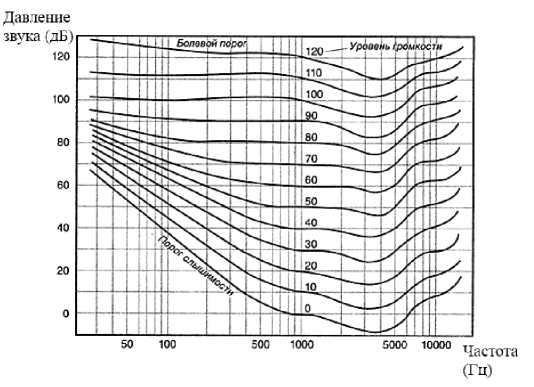
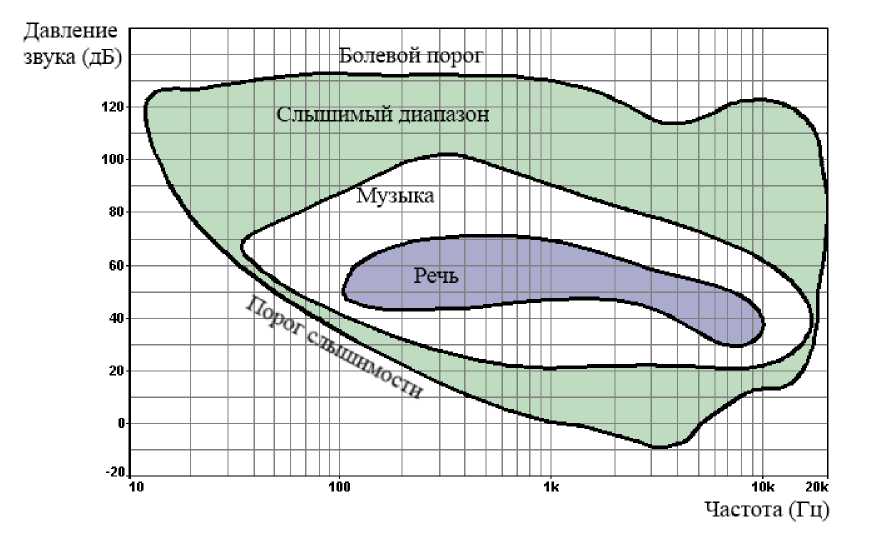
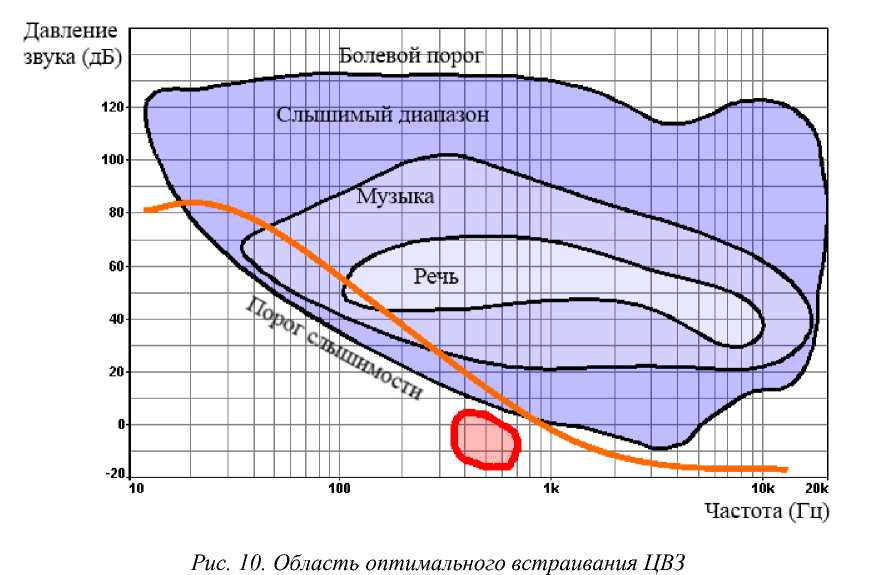
for (int i=0;i a1[i]=a[(i<<1)+1]; } vector vector vector double ang=2*pi/N*(inverse?-1:1); for (int k=0;k y[k]=y0[k]+w*y1[k]; y[k+n2]=y0[k]-w*y1[k]; if (inverse) { y[k]/=2; y[k+n2]/=2; } w*=wn; } return y; } Введем обозначение. Пусть A(x) — многочлен степени меньше N: N-1 A (x )=Z aix • i=0 Выделим отдельно члены четных и нечетных степеней A (x ) = A[0] (x2)+ xA[1] (x2) где N /2-1 A[0] (x)= Z a2ix , i=0 N /2-1 A[1] (x)= Z a2i+1 xi • i=0 В строках 3–5 формируется базис рекурсии. ДПФ для вектора длины 1 есть сам этот вектор, т.к. y 0 = a 0®1 = a 01 = a 0, где to. = j x, а ωxn ― комплексный корень степени n из x. В строках 12–16 формируются два новых вектора, первый из которых содержит элементы исходного вектора с четными индексами, а второй – с нечетными. К моменту выполнения строк 28 и 29, величина ωni уже посчитана. За счет строки 9 ее не нужно вычислять каждый раз заново; отсюда экономия по времени. В строках 18–19 рекурсивно вычисляются значения: y™ = A[0]^,2 ) y1" = A "’(toN, 2) Используя свойство k2k toN/2 = toN получаем .y 10] = A '“’toN*). У11= A'" (®N*) В строках 24–25 собираются результаты рекурсивных вычислений из строк 18–19. Для У 0, У1,..., yN 2-1 и 1 = 0,1,..., N 2-1 получается: У* = У10]+toNy 11 = A ™ (toN1)+toNA "'(toN- )= a (toN) Для yNj2, yN,2+1,..., yN-1 и 1 = 0,1,..., N/2 -1, используя свойства 1+N/ 2 NN 21 1+N toN ' =-toN, toN = 1, toN = toN , получается: y,+(Nу = y 1“’+ toNy?]= y10+ toN+N2 y[1 = = AI0(toN1)+toN+N2A111 (toN* )= = A[0](toN1+N)+ ton+N2A|1](mN1+N )= = A (toN,+N'2) Время, за которое процедура fftRecursive вычисляет БПФ, можно оценить как T (N) = 2T (N/ 2) + 0( N) = 0( N log N). Рассмотренный метод можно оптимизировать, заменив рекурсивный алгоритм итеративным. Последний имеет лучшие константы в асимптотической оценке ©(N log2N). Для начала можно убрать лишнее вычисление ωN y[1]введя дополнительную переменную. Получим: Подобное преобразование часто называют преобразованием бабочки из-за внешнего вида схемы вычислений (рис. 2). Рис. 2. Преобразование бабочки Теперь можно избавиться от рекурсии, заменив ее вычислением снизу вверх. Для этого расположим элементы в таком порядке, как в нижних листьях дерева на рис. 3. Рис. 3. Дерево входных веторов для процедуры fftRecursive при N = 8 Затем для пар элементов, стоящих на нижней строке дерева, вычислим ДПФ с помощью преобразования бабочки. Результатом будут значения второй снизу строки (полученные элементы можно записать на место исходного вектора, т.к. он больше не понадобится). Теперь из каждых двух пар векторов собираем две четверки и для каждой выполняем преобразование бабочки. Далее из полученных четверок собираются восьмерки и т.д. В общем случае на последнем шаге из двух векторов длины N 2 , являющихся преобразованиями Фурье четной и нечетной части вектора a , получается преобразование Фурье всего вектора a . Перед началом реализации нового алгоритма, необходимо перегруппировать элементы исходного вектора в следующем порядке: 0, 4, 2, 6, 1, 5, 3, 7 (при N = 8). Заметим, что эти индексы могут быть получены инверсией (реверсом) битов нормальной последовательности 0,1,...,N-1 (см. табл. 1). Таблица 1. Соответствие индексов с обычным и обратным порядком битов 0 ― 000 000 ― 0 1 ― 001 100 ― 4 2 ― 010 010 ― 2 3 ― 011 110 ― 6 4 ― 100 001 ― 1 5 ― 101 101 ― 5 6 ― 110 011 ― 3 7 ― 111 111 ― 7 Функцию, инвертирующую последовательность битов в исходном числе, можно записать так: Для дополнительной оптимизации можно выполнить следующие действия [14]: - вычислить заранее реверс битов для всех чисел (т.к. в программе длина вектора, над которым выполняется преобразование, есть константа, это легко сделать); - вычислить заранее все степени ω ; - использовать собственный класс для представления комплексных чисел; - перейти от хранения данных в vector к хранению в обычном массиве (эффект от замены зависит от компилятора). Также можно отдельно реализовать БПФ в виде явных формул для малых значений, например для N = 4. Как правило, изобретение этого метода в начале 1960-х годов приписывают ученым Кули и Тью-ки. В действительности этот метод неоднократно встречался и раньше, однако его важность стала ощутима только с появлением современных вычислительных машин. Считается, что этот алгоритм знали Рунге и Кёниг еще в 1924 году. Быстрое косинусное преобразование Научившись вычислять БПФ, можно составить алгоритм для подсчета БКП. Два этих преобразования тесно связаны между собой, и БКП вектора {x[m], m = 0,1,...,N -1} может быть получено через его БПФ. Для начала введем новый вектор {y[m], m = 0,1,... y [m ] = x [2 m ] y [N -1 - m ] = x [2 m +1] , N -1} следующим образом: (m = 0,1,..., N/ 2 -1). Тогда БКП для вектора x[m] можно записать так (для простоты опустим коэффициенты нормировки): N—1 М2 m +1) nn X[n] = Lx[mJcos| ------— m=0 V 2 N N 2-1 = Z x [2 m ]cosl m =0 V (4 m +1) nn ) N^1 1+ (4 m + 3) nn 2N 2 N J ml N 2-1 1 = Z У [m ]cos| m =0 (4 m +1)nn 2N Ni 2-1 , + Z У [ N -1 - m ]cos| m=0 (4 m + 3) nn 2N где первая сумма идет по четным индексам, а вторая по нечетным. Для второй суммы введем m' = N -1 - m, тогда пределы суммирования 0 и N/2 -1 для m становятся равными соответственно N -1 и N/2. Таким образом, вторая сумма принимает вид: N-! г fn (4m'+1)nn 1 N-J г f(4m'+1)nn . 7 yImOcos 2nn — -----— = 7 yImOcos -----— m '= N/ 2 V 2 N J m '= N/ 2 V 2 N Равенство возможно благодаря свойству cos(a — в ) = cos(a) cos(e) + sin (a )sin (в). Теперь две суммы в выражении для X[n] можно объединить в одну: 1 VC 1 f (4m +1)nn . X[n ] = E y[m]cosl -J m =0 V 2 N Заметим, что ДПФ от y[m] есть N—1 Y[n ]=E y[m e m=0 j2π --mn N N—1 =E y[m ] m=0 I 2nmn । . . f 2nmn cos|-------I— j sin l------- V N J V N . — inn / \ Z \ —f nn 1 f„nj nn 1 „ Если умножить обе части равенства на e2N = cosl I — j sinГ^^ I и взять действительные части от результата (учитывая, что x[m] и y[m] вещественные), получаем: —inn N-1 Re e2 NY [n ] = E y [m ] m=0 f 2nmn । f nn cosl-------I cosl---- V N J V2 N — . f2nmn 1 . fnn sin l---------I sin l----- V N J V2 N N-J г 1 f 4 m +1 1 = 7 y[m Icos ------nn . m=0 V 2N J Последнее равенство получено благодаря свойству cos(a — в ) = cos(a )cos(e)+ sin (a )sin (в) • Выражение для Re[e~v”n2NY[n]] идентично последнему выражению для X[n] откуда следует: —inn X [n ] = Re e2 NY [n ] , где Y[n] - ДПФ от последовательности y[m], определенной через x[m], которое может быть вычислено через БПФ за время ©(Nlog2N). В итоге БКП можно выполнить в четыре шага: - сформировать последовательность y[m] из x[m] - - y [m ] = x [2 m ] y [N — 1 — m ] = x [2 m +1] выполнить БПФ Y[n] для y[m] ; учесть коэффициент нормировки Y [n ] = C [n ]Y [n ], (m = 0,1,..., N/ 2 — 1); n = 0 C [n 1=1 ; n = 1,2,..., N — 1 - получить БКП X[n 1из Y[n]через выражение - X [n ] = Re - jn e ^Y [n ] При нахождении обратного БКП все действия выполняются в обратном порядке: сформировать последовательность Y[n]из X[n]учитывая коэффициент нормировки (На этом шаге также необходимо умножить все элементы на коэффициент 1 N , который появляется в обратном БПФ в строках 28–29. Однако поскольку вычисление обратного БПФ идет только в контексте обратного БКП, то этот коэффициент можно не учитывать ни там, ни сейчас): jπn Y [n ] = X [n ]C [n ]e ^N, n = 0,1, ... , N -1; - - получить y[m] из Y[n] через обратное БПФ и взять действительную часть от полученного результата; сформировать x[m] из y[m] x [2 m ] = y [m ] x [2 m +1] = y [N -1 - m ] (m = 0,1,..., N/ 2 -1). Программная реализация Перейдем к рассмотрению практической стороны вопроса. В качестве аудиосигнала выберем сигнал, записанный в wav-формате, поскольку данный формат довольно прост, бесплатен, широко распространен и не использует сжатия. Структура такого файла состоит из заголовка (в нем содержится информация о размере файла, количестве каналов, частоте дискретизации и глубине звучания) и области данных, состоящая из так называемых сэмплов (выборки значений функции от времени, описывающей звук). Формат заголовка представлен в таблице 2 [10, 11, 12, 13]. Таблица 2. Формат заголовка wav-файла Порядок байт Сдвиг Поле Длина поля Описание Секция прямой 0 ChunkID 4 'R', 'I', 'F', 'F' (ASCII) 0x52494646; началом RIFF-цепочки секция типа RIFF обратный 4 ChunkSize 4 file size - 8. 36 + subchunk2Size, или более точно: 4 + (8 + Sub-chunk1Size) + (8 + Subchunk2Size) прямой 8 Format 4 'W', 'A', 'V', 'E' (ASCII) 0x57415645 прямой 12 Subchunk1ID 4 'f', 'm', 't', ' ' (ASCII) 0x666d7420; в блоке fmt определен формат звуковых данных Секция формата – «fmt» обратный 16 Subchunk1Size 4 оставшийся размер подцепочки, начиная с этой позиции обратный 20 AudioFormat (Compression code) 2 код формата сжатия; для PCM = 1 (линейное квантование); значения, отличающиеся от 1, обозначают некоторый формат сжатия обратный 22 NumChannels 2 количество каналов (1 – моно, 2 – стерео и т.д.) обратный 24 SampleRate 4 частота дискретизации (кГц) обратный 28 ByteRate 4 количество байт, передаваемых за секунду воспроизведения (SampleRate * NumChannels * BitsPerSample / 8) обратный 32 BlockAlign 2 количество байт для одного сэмпла, включая все каналы (NumChannels * BitsPerSample / 8) обратный 34 BitsPerSample 2 количество бит в сэмпле; так называемая «глубина» или точность звучания. 8 бит, 16 бит и т.д. прямой 36 Subchunk2ID 4 'd', 'a', 't', 'a' (ASCII) 0x64617461 Секция данных – «data» обратный 40 Subchunk2Size 4 количество байт в области данных (NumSamples * NumChannels * BitsPerSample / 8) обратный 44 data аудиоданные Для обработки звуковых сигналов была создана программа на языке C++, которая способна загружать wav-файл и добавлять в него случайный водяной знак, а также сравнивать два сигнала – эталонный и проверяемый – делая вывод о наличии во втором водяного знака. Сам же цифровой водяной знак можно представить в разных форматах. В нашем случае это будет вектор случайных бит. Длина этого вектора будет зависеть от продолжительности аудиосигнала и размера стегоконтей-нера. При загрузке файла программа сначала считывает заголовок, оставшаяся часть файла записывается в буфер и разбивается на целое количество блоков, каждый из которых состоит из N каналов, где N =2n, n=2,3,4,..... Необходимость именно такой длины блока обуславливается особенностями быстрого косинусного преобразования. Из чего же будут состоять блоки? Каждый сэмпл в файле состоит из NumChannels каналов. Каждый канал в свою очередь определяется BlockAlign / NumChannels байтами. Поскольку в общем случае количество каналов в сэмпле неизвестно, составим блоки из всех байт только первого канала. Обозначим количество блоков через C . Остальные байты сэмпла не будут использоваться в программе. Их значения будут просто перенесены в формируемый сигнал с ЦВЗ. Последним считывается остаток файла, длина которого меньше N. В дальнейшем эта часть не будет фигурировать в вычислениях. Произведя загрузку файла программа готова добавлять в него ЦВЗ. Разложив сигнал на спектр определим, какие частоты будут являться стегоконтейнером. Для звукового сигнала такое разложение будет естественным, поскольку звук фактически является набором волн различной частоты и амплитуды. Чтобы обеспечить устойчивость (робастность) ЦВЗ, выбирать такие частоты нужно очень тщательно. Один из вариантов выбора – область наивысших (младших) частот, входящих в сигнал. Они в наименьшей мере определяют его вид, поэтому их изменение не вызовет слышимых помех. Выберем h таких частот. В таком случае фактическим контейнером водяного знака будет являться множество байт, соответствующих всему первому каналу. Это обуславливается тем, что даже незначительное изменение одной из частот разложения меняет весь сигнал. Итак, мы имеем C стегоконтейнеров, состоящих из N значений выбранного канала. Теперь можно выполнить C прямых преобразований с каждым из этих блоков. Результатом работы преобразований будут C векторов длины N , описывающих коэффициенты разложения на спектр частот. Первые коэффициенты полученных векторов соответствуют наиболее значимым (несущим) частотам, а последние ― младшим частотам. Соответственно наша цель – последние h частот. Практика показывает, что уже после 5й частоты вклад в вид сигнала каждой последующей несущественен. Основываясь на это можно взять h = N - 5 младших частот. Получив спектры разложений и выделив в них младшие частоты, нужно добавить наш ЦВЗ в полученный контейнер. Сделать это можно разными способами, например ослабив громкие частоты и усилив тихие. Для этого вводятся два дополнительных параметра T и α, где первый определяет порог амплитуды, а второй – величину изменения. Таким образом Н, f,< T fH f I a fj^ T i = 0,1,..., C -1; j = N - h -1, N - h,...,N -1. Введем правило, определяющее способ добавления битов знака в частотную область: ' fj wk = 0 f = ij a f4<T г = 0,1,..., C -1; j = N - h, N - h +1,..., N -1; wk = 1 k = zh + j + h - N; где w ― ЦВЗ и wk = (0,1,..., m), m = Ch. Применим это правило к отобранным частотам спектров и выполним C обратных преобразований. Из полученных новых блоков, неизмененных каналов, старого заголовка и неизмененного остатка соберем новый wav-файл. Также отдельно сохраним файл, содержащий битовую последовательность. Примеры результатов добавления ЦВЗ Рассмотрим несколько примеров работы программы в режиме добавления в ЦВЗ (рис. 4-7). Для этого построим спектрограммы сигналов до и после их изменений. Горизонтальная ось на графике – время, вертикальная – частота. Цвет точки определяет громкость данной частоты в данный момент времени. Спектрограммы построены с помощью программы Spek [15]. Рис. 4. Спектрограмма оригинального сигнала №1 Рис. 5. Спектрограмма сигнала №1 с ЦВЗ (n = 6, T = 100, α = 1.0005, h = 6) Рис. 6. Спектрограмма оригинального сигнала №2 Рис. 7. Спектрограмма сигнала №2 с ЦВЗ (n = 6, T = 100, α = 1.0005, h = 6) Как видно из иллюстраций, при выбранных значениях параметров встраивания ЦВЗ на спектрограмме могут появляться заметные отличия. Впрочем, на слух эти изменения заметить нельзя. Выбор частот для стегоконтейнера При выборе частот, которые будут изменены, предпочтение было отдано более высоким. Однако результат их изменения можно обнаружить на спектрограмме. Поэтому такие частоты являются не самым лучшим стегоконтейнером. Рассмотрим вариант с добавлением знака в средние частоты. Если аккуратно добавлять ЦВЗ именно в них, то можно добиться неслышимых изменений и усложнить задачу атакующему, стремящемуся избавиться от ЦВЗ. В случае с контейнером из высоких частот ЦВЗ можно легко убрать, просто удалив эти частоты из сигнала. Для средних частот удаление приведет к потере значимой части сигнала. Дополнительное усиление стойкости (робастности) ЦВЗ – случайный выбор частот из среднего диапазона. Поскольку атакующий не знает какие именно частоты содержат ЦВЗ, он будет вынужден избавиться от всех, что приведет к искажению сигнала. Какой же диапазон частот можно считать средним? В общем случае это зависит от конкретного сигнала. Будем считать частотой, находящейся в среднем диапазоне, такую частоту, которая близка к максимальной частоте, входящей в сигнал. Степень близости определяется шириной спектра. Чем он шире, тем шире средний диапазон. На спектрограмме этому диапазону соответствует участок перехода в зону черного цвета. Немаловажный фактор при выборе частот – чувствительность человеческого уха. Слышимую часть диапазона звуков разделяют на низкочастотные звуки – до 500 герц, среднечастотные – 500-10000 герц и высокочастотные – свыше 10000 герц. Такое разделение очень важно, так как ухо человека неодинаково чувствительно к разным звукам. Наиболее чувствительно ухо к сравнительно узкому диапазону среднечастотных звуков от 1000 до 5000 герц. К более низко- и высокочастотным звукам чувствительность резко падает. Это приводит к тому, что человек способен услышать в среднечастотном диапазоне звуки с энергией около 0 децибел и не слышать низкочастотные звуки в 20–40–60 децибел. Т.е. звуки с одной и той же энергией в среднечастотном диапазоне могут восприниматься как громкие, а в низкочастотном – как тихие или быть вовсе не слышны [16]. На рис. 8 представлены кривые равной громкости чистых тонов, называемые кривыми Флетчера-Мэнсона (Fletcher-Munson curves). Они показывают, что с уменьшением силы давления звука для обеспечения равной громкости требуется усиление по громкости на высоких и низких частотах. Рис. 8. Кривые Флетчера-Мэнсона Такая особенность звука сформирована природой не случайно. Звуки, необходимые для его существования – речь, звуки природы – находятся в основном в среднечастотном диапазоне. На рис. 9 показаны зоны, в которые попадают привычные нам звуки [17]. Рис. 9. Зоны слышимости Таким образом, наилучшим стегоконтейнером будут частоты, попадающие в область пересечения плохо слышимых зон со средним диапазоном сигнала. Чтобы получить величины частот, на которые раскладывает сигнал косинусное преобразование, в герцах нужно знать частоту дискретизации. Для этого воспользуемся теоремой Котельникова. Она утверждает, что для того чтобы однозначно и без потерь восстановить сигнал по точкам, максимальная частота в его спектре не должна превышать половину частоты дискретизации, т.е. fSR fmax < 2 . Зная, что частоты в спектре распределены равномерно получим выражение для n-й частоты: ■ n ] = fR/2n. N Тогда индекс коэффициента в векторе косинусного преобразования, определяющего амплитуду ближайшей от указанной частоты f, будет выражаться так: n = round f 2Nf 1V fSR / Так мы можем найти нужные нам (соответствующие амплитудам плохо слышимых частот) коэффициенты преобразования. Пусть теперь n и nh (0 < n< nh< N -1) - индексы амплитуд частот f [nl ] и f [nh ], таких, что частоты между f [nl ] и f [nh ] воспринимаются слабо. Определим множество таких частот: F1 = {f [k ] k = n, n +1,..., nh}. Теперь найдем множество частот из среднего диапазона сигнала F2 = {f [k] k = kо -5,kо -5 +1,...,k0,...,kо + 5 -1,kо + 5}, где k0 – индекс частоты, находящейся в середине этого диапазона, а δ – его ширина. Тогда стегоконтейнером будет следующее множество частот: F = Fx ПF2. Теперь остается только выбрать несколько случайных частот из этого множества и добавить в них биты ЦВЗ. Стоит отметить, что таких множеств может оказаться несколько. На рис. 10 показан пример выбора множества F. Черной линией показаны амплитуды частот сигнала в определенный момент времени, а оранжевая область – оптимальная зона встраивания знака. Описанный механизм на данный момент существует только в виде теории и не реализован в программе. На данный момент в программе можно вручную задать количество изменяемых частот и индекс первой такой частоты. Сравнение двух сигналов Во втором режиме работы программа сравнивает два сигнала и находит степень их похожести друг на друга. Для работы необходимы три следующих файла: - эталонный сигнал; - проверяемый сигнал; - битовая последовательность. Поскольку ЦВЗ располагается в частотной области, то на первом шаге после загрузки сигналов и разбиения их на блоки, выполняются прямые преобразования над этими блоками. Получив спектры сигналов, программа выделяет из проверяемого сигнала ЦВЗ. Для каждого очередного бита ЦВЗ, вычисляется исходное значение измененной частоты по формуле обратной формуле (10). Имея две частоты и заданную точность e можно выполнить их сравнение. Пусть w – реальный ЦВЗ, w' – выявляемый ЦВЗ, fk – одна из младших частот спектра эталонного сигнала и f 'k ― частота проверяемого сигнала после «удаления» бита ЦВЗ, тогда: wk \fk—V*kl < e w' k = < . j-wk Vk-f'k| ^ e Вычислив w' , программа сравнивает его с эталонным ЦВЗ. Сравнение может идти с помощью одного из двух способов: подсчет процента совпадений в битах знаков или корреляционным методом. Корреляционный метод сравнения Коэффициент корреляции показывает статистическую взаимосвязь двух или нескольких случайных величин. Коэффициент корреляции R для двух случайных величин X и Y , определённых на одном вероятностном пространстве задаётся формулой: cov(X,Y) X,Y = T5[x] • Ж], где cov(X, Y) – ковариация, D – дисперсия. Более развернутый вариант предыдущей формулы: R =_______M [XY ] — MX • MY_______ X, Y (M [X2 ]—(MX )2) J(M [Y2 ]—(MY )2), где . X (x1,..., xm ), m м (X ) = ~ £ x., m ,=1 1m M(XY ^-^ Х.-У.: m i=1 Величина RX Y имеет область значений [—1;1]. Чем она меньше по модулю, тем сильнее различия между X и Y . Заключение В статье описаны теоретические основы работы с цифровыми водяными знаками, базовые аспекты теории цифрового анализа сигналов и рассмотрены вопросы практического применения аналитических методов, таких как преобразование Фурье. Подробно описан один из алгоритмов вычисления быстрого преобразования Фурье, быстрого косинусное преобразование и выполнен анализ этих методов, направленный на оценивание скорости их работы. В тексте также содержится описание программы, в которой реализован метод добавления ЦВЗ в аудиосигнал и метод проверки его наличия. В основу этих методов был заложен итеративный алгоритм БКП, который был выбран среди множества других аналогичных алгоритмов на этапе анализа. С помощью данной программы были выполнены тесты по добавлению и проверке наличия ЦВЗ с различными сигналами. В результате чего выдвинута теория по оптимальному выбору стегоконтей-нера. Эта теория учитывает особенности человеческого восприятия звука и потенциальные варианты атак, нацеленных на удаление ЦВЗ. Также определены оптимальные значения параметров встраивания знака. Данное направление исследований подразумевает дальнейшее развитие. Так, например, открытым остается вопрос об использовании различных модификаций быстрого преобразования Фурье таких как преобразование в целых числах. Этот метод потенциально мог бы позволить достигнуть прироста вычислительной скорости и избавить от погрешностей при округлениях. Интерес также представляет проверка работоспособности теории по определению оптимального стегоконтейнера в аудиосигнале и анализ устойчивости сигнала.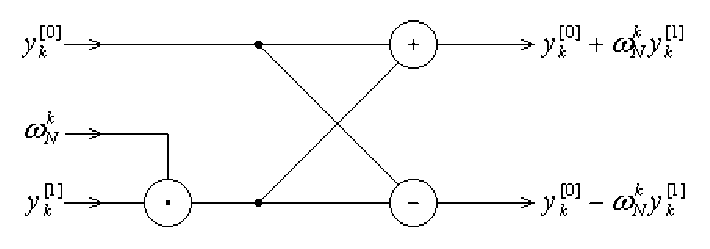
1
2
inline int reverseBits(int x, const int l) {
3
int res=0;
4
for (int j=0;j
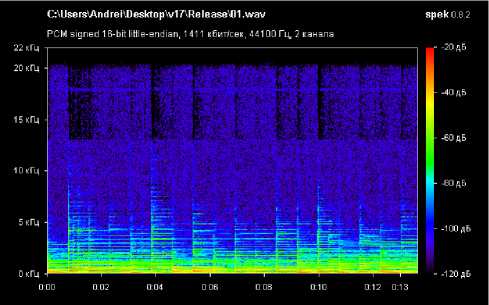
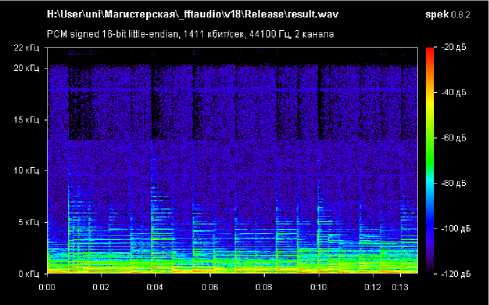
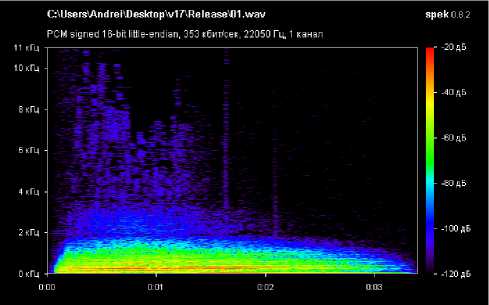
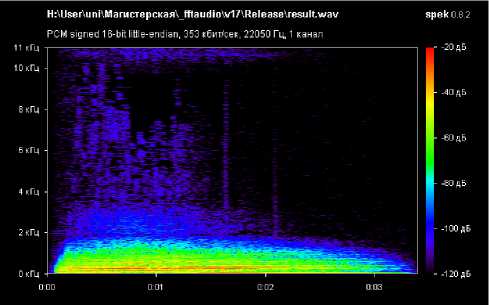
Список литературы Встраивание цифрового водяного знака в аудиосигнал с применением быстрого преобразования Фурье
- Грибунин В., Оков И., И. Туринцев. Цифровая стеганография. - М.: Солон-Пресс, 2002.
- Fourier transform. [Электронный ресурс]. URL: http://en.wikipedia.org/wiki/Fourier_transform.
- Discrete cosine transform. [Электронный ресурс]. URL: http://en.wikipedia.org/wiki/Discrete_cosine_transform.
- Chung-Bin Wu, Jiun-Lung Wang, Bin-Da Liu, Jar-Ferr Yang. Efficient Recursive Structures for DCT/IDCT // Department of Electrical Engineering National Cheng Kung University, Tainan, Taiwan, Republic of China. [Электронный ресурс]. URL: http://www.ee.nchu.edu.tw/Pic/Writings/2425_WCE99.PDF.
- Chan Yuk-Рee, Chau Lap-Pui, Siu Wan-chi. Efficient implementation of discrete cosine transform using recursive filter structure // IEEE transactions on circuits and systems for video technology. - 1994. - Vol. 4. - No. 6. - Pp. 550-552.


