Встраивание математической тепловой модели российского приборного комплекса ACS в общую модель европейского космического аппарата TGO миссии Exomars

При использовании российских приборов в зарубежных космических экспериментах возникают проблемы интегрирования российской аппаратуры в иностранный космический аппарат. Одной из таких проблем является сложность встраивания тепловых моделей отечественных приборов в общую модель аппарата из-за различных подходов к тепловому моделированию и различных используемых программных продуктов.

Подобную проблему пришлось решать после включения в состав аппаратуры европейской миссии ExoMars российского приборного комплекса Atmospheric Chemistry Suite ( ACS ). Задача осложнялась отсутствием времени на унификацию программных продуктов для теплового моделирования. Данная проблема была решена путем создания узловых математических моделей приборов, пригодных одновременно как для отечественных программных продуктов, так и для программ теплового моделирования, используемых в ESA . В связи с развитием международного сотрудничества в области научных космических экспериментов данный опыт может оказаться полезным для будущих международных миссий.

Использование узлового метода для сопряжения тепловых моделей ACS и приборного комплекса ExoMars

ACS представляет собой набор из трех инфракрасных спектрометров ( MIR, NIR, TIRVIM ) и обслуживающего их блока электроники (БЭ) [1]. Комплекс предназначен для изучения химического состава и структуры атмосферы Марса. Размер ACS составляет 470×517×557 мм, масса 30 кг.

Данный комплекс размещается на европейском орбитальном модуле Trace Gas Orbiter ( TGO ).

На рис. 1 показаны комплекс ACS и орбитальный модуль TGO. ACS резко выделяется на общем фоне модуля из-за различия цвета отечественной и европейской экранно-вакуумной теплоизоляции (ЭВТИ).

Рис. 1. Приборный комплекс ACS отдельно (слева) и в составе орбитального модуля TGO: TGO (Trace Gas Orbiter) — орбитальный модуль; MIR (Mid-infrared), NIR (Near-infrared), TIRVIM (Thermal-infrared) — спектрометры ACS; БЭ — блок электроники ACS

Неприменимость математической тепловой модели ACS для общей тепловой модели космического аппарата стала очевидной на стадии предъявления требований ESA к российским приборам, в соответствии с которыми их модели должны быть представлены в формате компьютерного комплекса ESATAN [2], мало используемого в России. При этом тепловая модель ACS начального уровня должна была быть предоставлена практически сразу после принятия решения о включении российских приборов в состав научной аппаратуры ExoMars , что не давало времени на приобретение и освоение пакета ESATAN .

Препятствием для сопряжения моделей являлось не только несоответствие используемых программных продуктов, но и различный подход к моделированию. В отечественной практике для тепловых расчетов обычно применяются конечноэлементные модели, в то время как в Европе для некоторых задач, в частности, для объединения моделей приборов в модель приборного комплекса, используются математические узловые модели.

Конечноэлементная модель формируется в результате деления трехмерной модели объекта на малые части — конечные элементы. Их вершины назначаются узлами, теплообмен между которыми происходит через объем конечного элемента [3]. При этом удовлетворительный результат моделирования для сложного объекта получается только при малых размерах конечных элементов и, как следствие, при большом их количестве — от десятков тысяч до миллионов. Таким образом, конечноэлементный метод изначально ориентирован на наличие значительных компьютерных ресурсов.

В основе узловой модели лежит метод графов, позволяющий значительно сократить количество расчетных тепловых узлов в модели объекта за счет введения параметра эффективной тепловой связи между удаленными тепловыми узлами, рассматривая структуру объекта между ними в качестве их теплового соединителя [4]. Данный метод широко использовался до появления высокопроизводительных компьютеров [5].

Возвращение к узловому методу в настоящее время, когда компьютерные ресурсы не создают существенных ограничений для конечноэлементного моделирования, происходит из-за качественных преимуществ узлового метода.

К таким преимуществам относятся [4]:

• •    прямой доступ к параметрам математической модели, который позволяет контролировать достоверность расчета на

всех этапах моделирования и выявлять параметры, вносящие наибольший вклад в ошибку;

• •    возможность исследования влияния каждого параметра модели на температурный режим и возможность определения оптимальных характеристик системы обеспечения теплового режима итерационным методом, которые обеспечиваются за счет того, что для каждой итерации требуются незначительные расчетные ресурсы;

• •    наличие формализованных алгоритмов корректировки узловой математической модели по результатам эксперимента;

• •    простота интегрирования нескольких тепловых моделей в одну объединенную модель.

Ни одна из этих процедур не может быть выполнена с помощью конечноэлементного метода из-за отсутствия внешнего доступа к параметрам десятков или сотен тысяч уравнений, составляющих математическую модель.

Однако и узловой метод не свободен от недостатков. Самым существенным из них является заведомо неверное предположение об изотермичности значительных фрагментов конструкции, объединенных в тепловые узлы.

Компьютерное приложение ESATAN основано на узловом методе моделирования. Именно этот фактор позволил с помощью отечественного программного продукта создать тепловые математические узловые модели российских приборов, применимые для ESATAN , точнее, для его составной части — Thermal Excel , в которой далее и проводилось основное моделирование теплового режима аппарата.

Для этого была использована разработанная в ИКИ РАН программа теплового моделирования ThermNS ( Thermal Nodal Simulation ). В ней используются динамические (зависящие от времени τ ) уравнения, описывающие теплообмен в системе, состоящей из n тепловых узлов. Для i -го узла, имеющего температуру T_i , данное уравнение имеет следующий вид:

^ с - QXO - S dт            ^1

(i j )

(Т, ( т ) - Т( т ))

R i–j

+ F.(/Ц(Е (т) + Е t(т)) + 8(£ Хт) - n

- F ' - Е

; -1

( i *; )

фF' - F‘ ij

^{1+ ф} f ‘ - f ‘ ij

i iL

ТТ- ^{- 1 + ф} f ‘ ε j

- f ‘ i

^ -¹ ε _j

( Т 4 ( т ) - т ; ( т )).

В этом уравнении тепловыми свойствами i -го узла являются: теплоемкость C_i , внутреннее тепловыделение Q_i , площадь F_i , коэффициент поглощения солнечного излучения As i и степень черноты s i поверхности внешнего теплообмена; площадь F' и степень черноты s' поверхности внутреннего теплообмена. Параметром кондуктивной тепловой связи i -го и j -го узлов является тепловое сопротивление между узлами R_{i – j} , радиационной тепловой связи — их взаимные угловые коэффициенты Ф_г__г и Ф_г__г = Ф_г__г( F' / F ' ). Внешние тепловые условия содержат воздействующие на узел тепловые потоки от внешних источников: прямое Es_i и отраженное Esp_i солнечное излучение, инфракрасное излучение Ep_i , а также угловой коэффициент поверхности внешнего теплообмена по отношению к космосу ф F _ S . В уравнение входит постоянная Стефана-Больцмана ст .

Программа Thermal Excel использует подобные уравнения, но с параметрами другого вида. Вместо теплового сопротивления используется тепловая проводимость s_{i – j} = 1/ R_i–j . Радиационная тепловая связь между узлами описывается эффективным комплексным параметром:

Ie i – j

σϕ     F ′

F ′ – F ′ i ij

^{1 +} Ф Г ' - Г '

ij

1 _{ε ′}

+ Ф г ’ — г '

ji

ε¹ ′ – 1

Кроме того, в этой программе поверхность каждого узла аппроксимируется набором плоских четырехугольных фрагментов и описывается координатами их вершин: (( x ₁ , y ₁ , z ₁ , x ₂ , y ₂ , z ₂ , x ₃ , y ₃ , z ₃ , x ₄ , y ₄ , z ₄ ) ₁ , …) _i , которые являются основой для вычисления площадей F_i и F'_i и взаимных угловых коэффициентов поверхностей узлов ф _F, _ _F , . j i

Таким образом, взаимодействие между программами ThermNS и Thermal Excel и, соответственно, между группами теплового моделирования в России и Европе удалось организовать путем прямого и обратного переформатирования параметров, используемых в программах ThermNS и Thermal Excel .

Это позволило интегрировать тепловую узловую модель ACS в общую модель космического аппарата. На рис. 2 показан геометрический уровень данной интеграции.

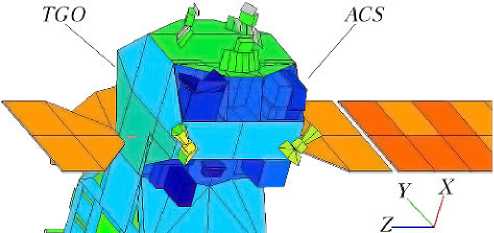
Рис. 2. Геометрическая составляющая узловой тепловой модели TGO с интегрированной моделью ACS

Оптимальное использование узловой модели на этапах создания ACS

Возможность адаптации узловой модели к любой степени детализации конструкции прибора позволила использовать ее для решения различных задач в течение всего цикла создания ACS от формирования облика прибора до корректировки модели по результатам тепловакуумных испытаний.

Первая оценочная тепловая узловая модель ACS была разработана до формирования окончательного облика прибора и служила для оптимизации ориентации и площадей радиаторов. Данная модель начального уровня базировалась на предварительной конструктивной схеме и циклограмме включения приборного комплекса, а также на информации о месте его установки на TGO и разрешенных зонах размещения радиаторов. Модель содержала 17 тепловых узлов, включая три радиатора, являющихся объектами оптимизации. Оптимизация проводилась для трех тепловых режимов ACS : режима перелета (выживания) и режимов функционирования на двухчасовой марсианской орбите при минимальной (-30 ° С) и максимальной (+50 ° С) температурах посадочных мест ACS , далее называемых «минимальным» и «максимальным».

Несмотря на свою простоту и, во многом, условность, оценочная модель позволила определить и сразу заложить в проектируемую конструкцию оптимальные площади и ориентацию радиаторов. Для этого была рассчитана зависимость стационарной температуры узлов тепловой модели ACS от площадей радиаторов входящих в него приборов (рис. 3) при различных тепловых режимах. Из этой зависимости были выбраны площади, обеспечивающие допустимый тепловой режим для всех приборов на всех этапах эксплуатации.

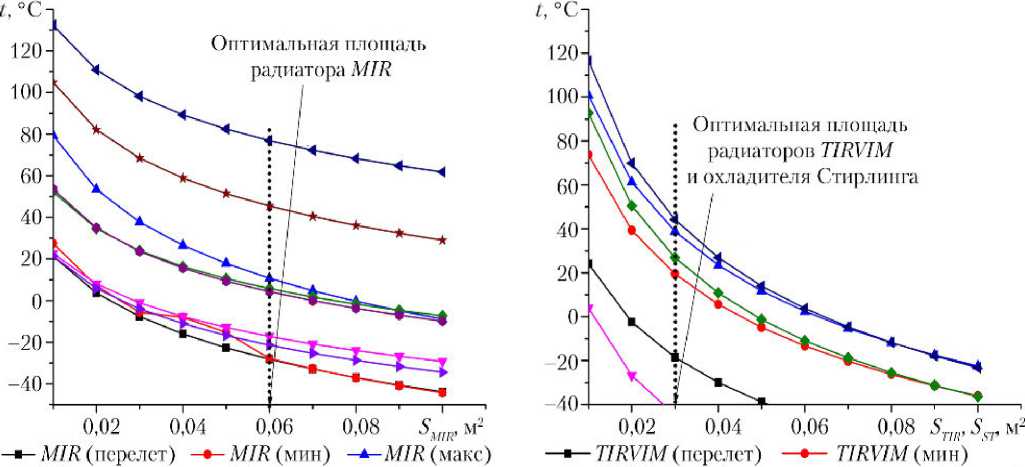
-т-MR (перелет) —♦—MR (мин) —n— MR (макс)     —*—TTRVIM (макс?)    —v—Стирлинг (перелет)

—>— БЭ (перелет) —•— БЭ(мин) —*— БЭ (макс)     —♦—Стирлинг (мин) —♦—Охладитель (макс)

Рис. 3. Расчетная зависимость температуры узлов оценочной модели ACS от площадей радиаторов MIR (SMIR ), TIRVIM (STIR ) и охладителя Стирлинга (SST ) при различных тепловых режимах

Примечание. БЭ — блок электроники; «мин» — орбитальный полет, температура посадочных мест -30 ° С; «макс» — орбитальный полет, температура посадочных мест +50 ° С.

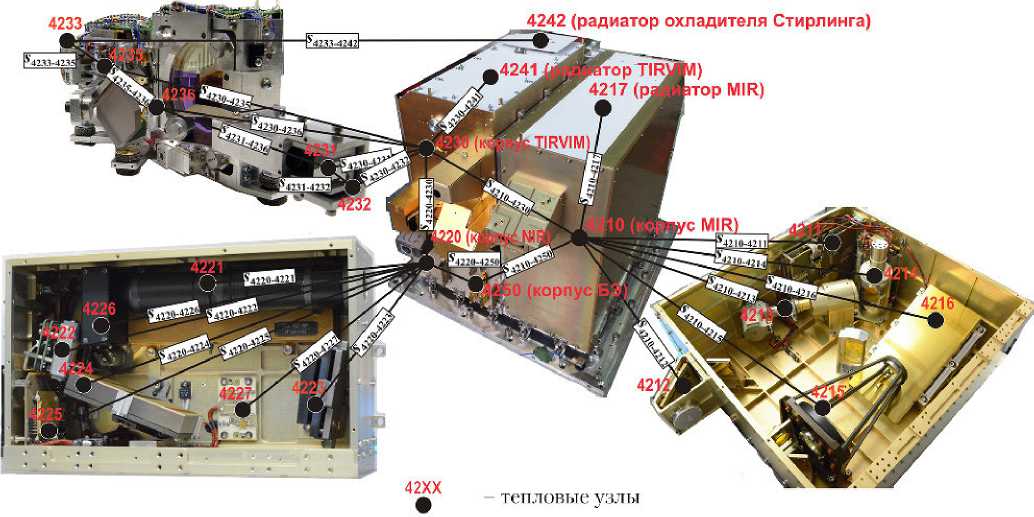
Далее узловая модель ACS прошла восемь этапов уточнения, в процессе которых количество узлов возросло с 17 до 39. Последняя версия модели представлена на рис. 4. Использование для нумерации тепловых узлов ACS формата 42XX связано с тем, что данный диапазон номеров был зарезервирован для ACS в общей тепловой модели орбитального модуля.

На каждом этапе проводилось именно развитие модели путем добавления узлов и изменения некоторых их параметров, а не полная замена предшествующей модели на новую.

— 1*'42..-42„| -- проводимости тепловых связей

Рис. 4. Узловая тепловая модель ACS без экранно-вакуумной теплоизоляции (ЭВТИ)

Примечание. Соответствие узлов тепловой модели составным частям ACS : 4210–4217 — MIR ; 4220–4227 — NIR ; 4230–4236, 4241, 4242 — TIRVIM ; 4250, 4251 (не показан) — блок электроники; узлы, соответствующие фрагментам ЭВТИ (4261–4267), не показаны.

Налаженное взаимодействие между программами ThermNS и Thermal Excel позволило не только передавать европейским партнерам обновленные варианты модели, но и использовать их результаты моделирования температуры конструкции аппарата, окружающей приборный комплекс ACS . Для этого в состав сформированной в ThermNS модели были введены узлы, соответствующие элементам конструкции аппарата, находящимся в зоне видимости со стороны поверхности ACS и в тепловом контакте с его посадочными местами. Температуры этих узлов назначались на основании результатов теплового моделирования TGO в целом.

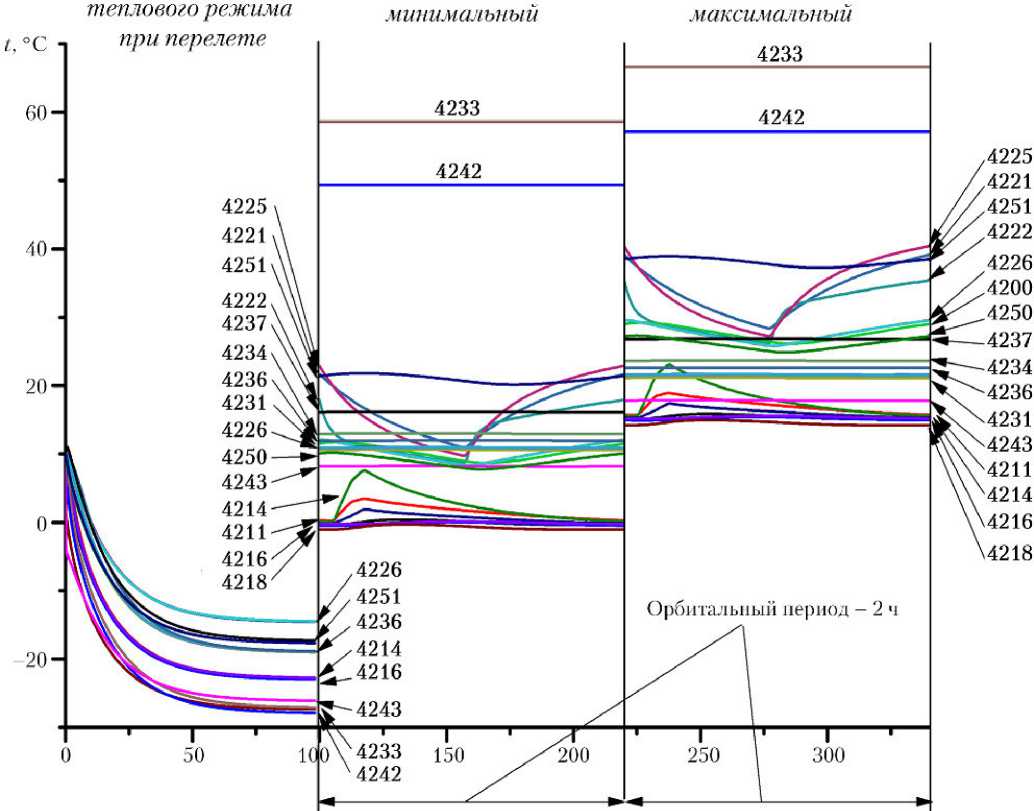
Итоговые результаты теплового моделирования режима перелета и двух граничных тепловых режимов при орбитальном полете вокруг Марса представлены на рис. 5.

В процессе моделирования узловая модель продемонстрировала еще одно полезное свойство, заключающееся в возможности ее адаптации к специальным задачам. Такой задачей в процессе теплового моделирования являлась оценка аэродинамического нагрева ЭВТИ прибора при прохождении аппаратом верхних слоев атмосферы Марса и одновременном облучении прямым солнечным излучением. Для решения этой задачи в состав модели были введены узлы, описывающие фрагменты ЭВТИ, перпендикулярные набегающему газовому потоку. Полученные при этом оценки температуры ЭВТИ (рис. 6) показали, что для теплоизоляции необходимо использовать более термостойкие материалы по сравнению с выбранными первоначально.

Охлаждение до стационарного

Тепловые режимы при орбитальном полете

т, ч т, мин

Рис. 5. Результаты расчета температуры тепловых узлов модели АCS при различных тепловых режимах

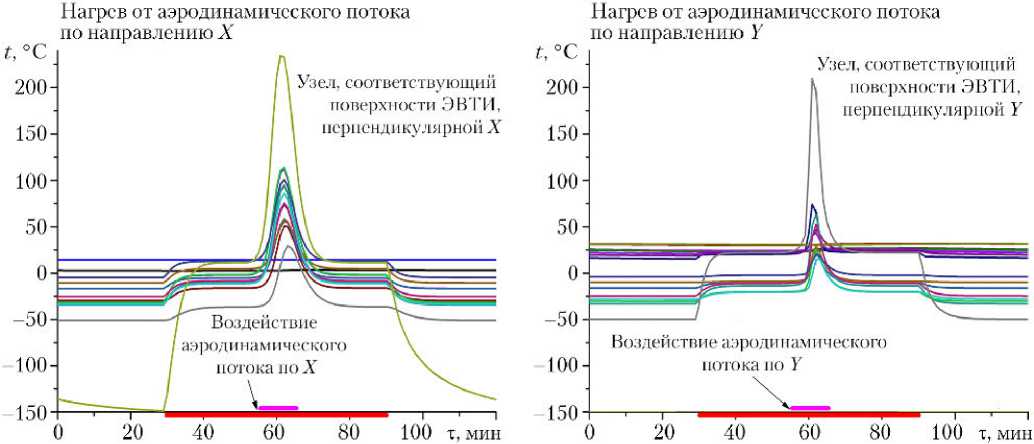
Рис. 6. Математическое моделирование нагрева тепловых узлов модели АCS при прохождении верхних слоев атмосферы Марса при направлении скорости набегающего потока по -X и -Y: ■ — воздействие солнечного потока

Корректировка узловой модели ACS по результатам наземного эксперимента и подтверждение корректности модели результатами летного эксперимента

Одним из самых полезных свойств узловой модели является наличие математически строгого алгоритма ее корректировки (или даже формирования) по результатам эксперимента. Данный алгоритм описан в источнике [6]. Для ACS была применена комбинация аналитического и экспериментально-аналитического методов восстановления характеристик тепловых узлов из экспериментальных данных. По результатам эксперимента корректировались те характеристики узловой модели, которые практически невозможно было рассчитать аналитическим методом: тепловые проводимости между составляющими приборный комплекс приборами ( MIR и TIRVIM — s _4210–4230 ; MIR и БЭ — ^s 4210–4250 ^; NIR и TIRVIM — s _4220–4230 ; NIR и БЭ — s 4220–4250 ; TIRVIM и БЭ — s 4230–4250 ), а также эффективная удельная тепло-проницаемость ЭВТИ r_MLI [К·м ² /Вт], определяющая эффективные теплопроница-емости ЭВТИ приборов MIR — s , 4210–4261

s4210–4262; NIR — s4220–4263, s4230–4265, s4230–4266; БЭ — s4250–4267.

s 4220–4264 ; TIRVIM —

В основе   экспериментально-анали- тического метода лежит решение обрат- ной задачи с известными из эксперимен- та температурами и тепловыми потоками и неизвестными тепловыми характеристиками узлов модели. Для реализации этого метода используется матричный вид системы уравнений (1): Ax = b, в котором A — основная матрица; x — вектор уточняемых параметров; b — столбец свободных членов. В матричном виде вектор x определялся на основании критерия минимизации суммы квадратов отклонений реальных значений уравнений от значений свободных членов: ((Ax – b)T(Ax – b)→min) → →ATAx = ATb → x = (ATA)–1b.

Адаптированный для ACS набор матриц ( A , x , b ) имеет вид:

T ₄₂₁₀ ( τ₁ ) – T ₄₂₃₀ ( τ₁ ) ...             0

...

;

0            ... T ₄₂₆₇ ( τ₆ ) – T ₄₂₅₀ ( τ₆ )

b =

^Q 4210 ^(τ 1 ⁾

^{d T} 4210 ^{( τ} 1 ⁾ d τ

^C 4210 ^{– F} 4210 ^ε 4210 ^{( Ep} 4210 ^(τ 1 ^{) – ϕ} F   – S ^{σ T} 4210 ^(τ 1 ^{)) –} Σ     ^Ie 4210– j

⁴²¹⁰                        j = 4211

^Q 4267 ^(τ 6 ⁾

^{d T} 4267 ^{( τ} 6 ⁾ d τ

^C 4267 ^{– F} 4267 ^ε 4267 ^{( Ep} 4267 ^(τ 6 ^{) – ϕ} F ₄₂₆₇– S ^{σ T 4} 4267 ^(τ 6 ^{)) –} Σ     ^Ie 4267– j

⁴²⁶⁷                       j = 4210

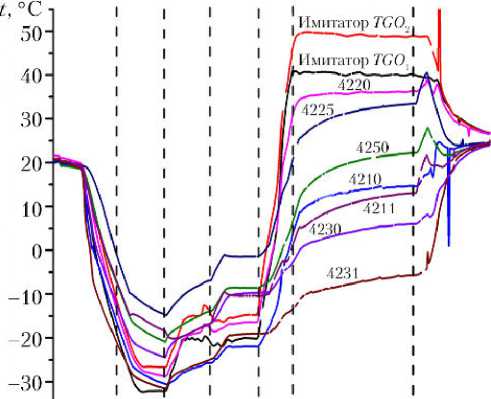
Для формирования матрицы A и столбца b были использованы результаты тепловакуумных испытаний теплового эквивалента ACS (рис. 7).

а)

_______________ ^IT"

О ' 10 ' 2*0 ' з’о ' 40 ' 50 ' б'о т,ч б)

Рис. 7. Тепловой эквивалент ACS перед установкой в вакуумную камеру (а) и зависимости температур узлов тепловой модели от времени, измеренные в процессе испытаний (б)

Исходя из количества уточняемых тепловых характеристик узловой модели (s4210–4230, s4210–4250, s4220–4230, s4220–4250, s4230–4250, rMLI), были использованы шесть моментов вре- мени (т1, т2, ., тк, ... матриц A и b,

., т6) для формирования в которых для каж- дого узла i модели фиксировались значения температур T(тк) = ti(тк) + 273,15 и тепловых потоков Qi(тк), Epi(тк). При этом два набора измеренных параме-трое (в т2 и т4) соответствовали условно стационарным тепловым режимам dTi(тк)/dт = 0. В остальных случаях необходимо было оценить производные температур dTi(тк)/dт « (Ti(тк+ Ат) - Ti(тк))/Ат.

С помощью сформированных матриц были вычислены компоненты вектора уточняемых параметров. Результаты вычисления показали, что все эти параметры нуждались в существенной корректировке. Так, в частности, была скорректирована эффективная теплопроницае-мость ЭВТИ с 35 до 29 К·м ² /Вт, которая всегда имеет значительный разброс из-за существенного влияния геометрии поверхности изоляции. Проведенная корректировка позволила существенно повысить достоверность модели. Отличие расчетных и экспериментальных значений температур, которое в некоторых узлах модели до корректировки достигало 10 ° С, после нее было снижено до 2 ° С.

Космический аппарат ExoMars был запущен 14 марта 2016 г. Через несколько суток был гарантированно достигнут стационарный тепловой режим, что дало возможность провести прямое сравнение результатов математического моделирования с реальными телеметрическими данными. Информация поступала с четырех температурных датчиков. На рис. 8 показаны соответствующий стационарному тепловому режиму фрагмент телеметрической информации о температурах ACS в период с 30.03.2016 г. по 01.04.2016 г. и результаты математического моделирования температур ACS в точках установки температурных датчиков на этапе перелета.

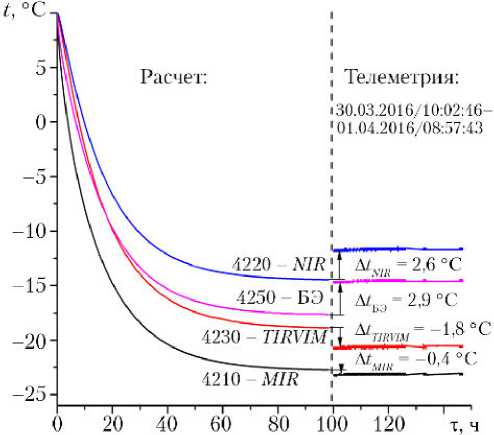
Рис. 8. Результаты математического моделирования температур в четырех точках ACS на этапе перелета и реальная телеметрическая информация об этих температурах

Отличие расчетных значений температур от реальных в измеряемых точках составляет -1,8...+2,9 ° С. Это показывает, что экспериментально аналитический метод позволяет скорректировать ошибки узловой модели, возникающие из-за допущения изотермичности значительных фрагментов конструкции. Это, в свою очередь, дает возможность использовать узловую модель не только в качестве оценочной, но и как основной инструмент для расчета тепловых режимов космических устройств.

Заключение

При реализации международных космических проектов возникают проблемы математического теплового моделирования из-за сложности сборки в объединенную модель разных приборов, создаваемых научными группами, использующими различный подход к тепловому моделированию. Опыт создания российского прибора ACS для международного проекта ExoMars показал, что данные проблемы могут быть решены за счет использования основанного на методе графов узлового метода теплового моделирования для всех приборов научной аппаратуры. При таком подходе использование различных программных продуктов не является препятствием для создания объединенной математической тепловой модели, поскольку метод позволяет легко создать межпрограммные трансляторы.

По сравнению с более сложными конечноэлементными моделями узловые модели имеют ряд преимуществ, делающих их необходимыми не только для объединения моделей нескольких приборов, но и для моделирования тепловых режимов одиночного прибора. К таким преимуществам относится, в частности, возможность решения оптимизационных задач и наличие формализованных алгоритмов корректировки узловой модели по результатам теплового эксперимента.

Такая корректировка дает возможность повысить достоверность узловой модели до уровня, позволяющего делать не только приближенную оценку температур, но и полноценный тепловой расчет. Это подтверждается сравнением итоговых результатов математического моделирования тепловых режимов российского прибора ACS проекта ExoMars с телеметрическими показаниями температурных датчиков, установленных на данном приборе.