Вторая структура постоянного тока

В [1-3] было показано, что постоянный ток в проводе имеет сложную структуру, а поток электромагнитной энергии распространяется внутри провода. При этом поток электромагнитной энергии

• •    направлен вдоль оси провода,

• •    распространяется вдоль оси провода,

• •    распространяется внутри провода,

• •    компенсирует тепловые потери осевой составляющей тока.

• 2.    Математическая модель

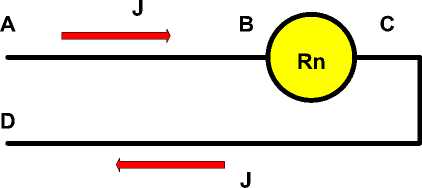
Рис. 1.

В [1-3] была предложена и рассматривалась математическая модель тока и потока, построенная исключительно на уравнениях Максвелла. Остался невыясненным следующий вопрос – см. рис. 1. Электрический J ток и поток электромагнитной энергии S распространяется внутри провода ABCD и проходит через нагрузку Rn . В этой нагрузке расходуется некоторая мощность P. Следовательно, поток энергии на участке AB должен быть больше потока энергии на участке CD . Точнее, Sab=Scd+P. Однако сила тока после прохождения нагрузки не изменилась. Как должна измениться структура тока, чтобы уменьшилась соответствующая ему электромагнитная энергия?

Ниже рассматривается более общая (по сравнению с [1-3]) математическая модель, позволяющая ответить и на этот вопрос. Эта математическая модель также построена исключительно на уравнениях Максвелла. В [4] описывается эксперимент, который был выполнен группой авторов в 2008 г. В [5] показано, что этот эксперимент может быть объяснен на основании нелинейной структуры постоянного тока в проводе и может служить экспериментальным доказательством существования такой структуры.

При моделировании будем использовать цилиндрические координаты r, ф , z и рассматривать

• •    основной ток J_o ,

• •    дополнительные токи J r , J J z ,

• •    магнитные напряженности H r , Н _ф , H z ,

• •    электрические напряженности E ,

• •    электросопротивление ρ .

Ток в проводе принято рассматривать как усредненный поток электронов. Механические взаимодействия электронов с атомами считаются эквивалентными электрическому сопротивлению. Очевидно,

E = ρ ⋅ J .                                                  (1)

Основной ток с плотностью J_o создает дополнительные токи с плотностями J r , J J_z и магнитные поля с напряженностями H r , Н _ф , H_z • Они должны удовлетворять уравнениям Максвелла.

Эти уравнения для магнитных напряженностей и токов в стационарном магнитном поле имеют вид rot(H) = J,

Кроме того, токи должны удовлетворять условию непрерывности

div( J ) = 0 .	(4)
Уравнения (2-4) для цилиндрических координат имеют вид: Hr д Hr 1 5 H   д Hz_ +     + *     +      = 0 , r     д r   r дф    д z	(5)
1 5 h z а Н ф *                  = J r , r Э ф д z	(6)
d H r H L = J a z      a r      ф ’	(7)
Н ф + d Н ф  1 5 H r +           *      = J z , r     д r   r д ф	(8)
Jr   j  1 д J ,   j 111= 0 • r    д r   r дф   д z	(9)
Для сокращения записи в дальнейшем будем применять следующие обозначения:
co = - cos(аф + xz ) ,	(10)
si = sin( аф + xz ) ,	(11)
где а , x — некоторые константы. В приложении 1 показано,	что
существует решение, имеющее следующий вид: Jr • = Jr ( r ) co ,	(12)
J ф • = ф ( r ) si ,	(13)
J • = j z ( r ) si ,	(14)
H r • = hr ( r )C ° ,	(15)
Н ф . = h ф ( r ) si ,	(16)
H z • = h z ( r ) si ,	(17)
где j ( r ), h ( r ) - некоторые функции координаты r .

Можно полагать, что средняя скорость электрических зарядов не зависит от направления тока. В частности, при фиксированном радиусе путь, пройденный зарядом по окружности, и путь, пройденный им по вертикали будут равны. Следовательно, при фиксированном радиусе можно полагать, что Дф = Az . На основе этого предположения можно построить траекторию движения заряда в соответствии с функциями (10, 11).

На рис. 2 показаны три винтовые линии при Д . = A z , описываемые функциями (10, 11) тока: толстая линия при а = 2, х = 0-8 , средняя линия при а = 0.5, X = 2 и тонкая линия при а = 2, х = 1-6 .

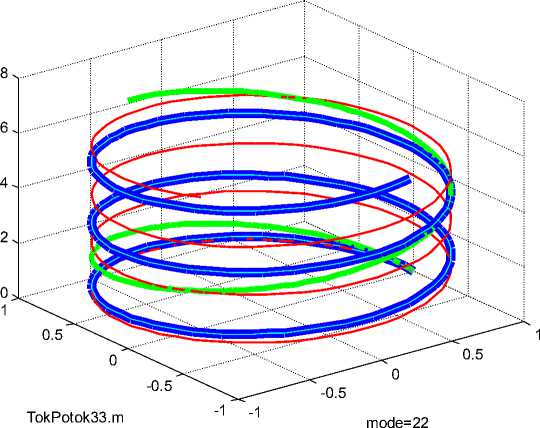
Рис. 2.

В приложении 1 показано, что функции удовлетворяют следующим уравнениям:

h (r) = 0,

Ж hr(r)+ h^ а = 0,(21)

• -    h. (r) X = j, (r)

• -    hr (r X = j.(r) ,(23)

^ + h. (r) + - • h, (r )а = jz (r) .(24)

rr

Эта система уравнений недоопределена – имеется 4 уравнения (21-24) для 5 переменных jr, j., jz, hr, h.. Важно отметить, что hz (r) = 0. Если одна из переменных известна, то остальные определяются дифференцированием этой системы уравнений.

Например, при известной функции h ^ ( r ) находим:

hr(r )=-hrtr)'_ h^rt a, rr jr (r)=-h^ (r)X, j^(r) = -hr (r )X, , (25) (26) (27) h (r)             1

j_z ⁽ r ) =       + Н _ф ⁽ r ) + • h r ⁽ )z. .                          ( 2 8)

rr

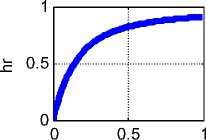
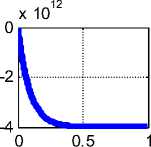
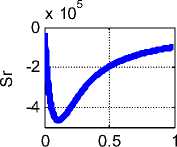
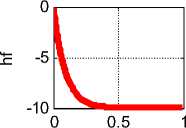
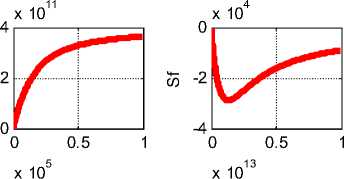
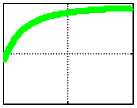
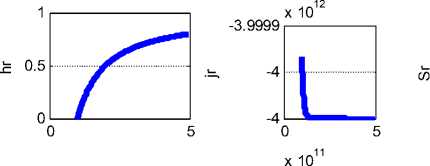
Пример 1. Пусть, например, h ^ ( r ) = 10 • ( e ^{11000 r} - 1). На рис. 3

показаны графики функций j_r ( r ), j ^ (r ), j_z ( r ), hr ( r ), h ^ (r ), h_z ( r ) .

Эти функции вычисляются при данных а = 0.1, X = —4•Ю11, радиусе провода R = 0.001 и начальном условии jr (0) = 0. В первой колонке показаны функции jr (r), j^(r), jz (r) , во второй колонке показаны функции hr (r), h^(r), hz (r), а функции, показанные в третьей колонке, будут рассмотрены далее. Здесь и далее все числовые результаты представлены в системе СИ. На оси абсцисс показаны величины (1000r).

-1

0      0.5       1

-1

N,

0      0.5

Fig.3. TokPotok33.m, mode=41

-2

N

V)

0      0.5

-10 0

-9.9998

-9.9999

т

x 104 0

-5

-10 0

-2000

-4000 05

-1 0

-2

x 104

-1

т

Fig.4. TokPotok33.m, mode=3

3.96 0

x 10

3.98

Пример 2 . Кроме

сплошного провода можно рассмотреть

трубчатый проводник. В этом примере к_ф ( г ) = 10 • ( е ¹¹⁰⁰° r

рис. 4 показаны графики функций j r ( r ), j ( r ), j_z ( r ), h r ( r ), h _ф ( r ), h_z ( r ) . Эти функции вычисляются при а = 0.1, X = ^_ 4 - 10¹¹. Основное отличие состоит в том, что область интегрирования ограничена: R 1 <  r <  R , причем R = 0.005, R 1 = 0.2 • R , и начальное условие j, ( R 1 ) = 0 .

3. Потоки энергии

Плотность потока электромагнитной энергии Пойнтинга

S = E х H.

–

вектор

Токам соответствуют одноименные электрические напряженности, т.е.

E = Р-J, где ρ - электросопротивление. Совмещая (1, 2), получаем:

S = pJ х H.

В цилиндрических координатах r , ф , z плотность

потока

электромагнитной энергии имеет три компоненты S r , S _ф , S z ,

направленные	вдоль			радиуса,		по	окружности, вдоль			оси
соответственно.	Они определяются					по формуле
	" S	1				" J p H z	- J z H p "
S =	S	P	= p ( J x H ) = p			J z H r	- J , h	z J	.	(4)
	_ S	J				_ J r H p	- J p H r J
Из (2.12-2.17, 3.4) следует, что
	Г S	1 r			(j'.ph^z -	j z h p )	si 2
S =	S	ϕ	= p JJJ		( J\hrr -	j r h z )-	si • co	dr • dp • dz .		(5)
	_ S	z J	r , ϕ , z		_ ( / r h p -	j p hr )	si • co
На рис. 3 и рис.	4 показаны функции
		" S, ( r )			( jPph'z -	j z h p ^^
S ( r ) =		S t)		=	( J'hrr -	j r h z )	.			(6)
		£ (r )			_ ( / r h p -	Jphr )_
Из (4), как показано в приложении 2, следует
S = p •< 4 α	1 -	cos ( 4 an )) J ( S z ( r ) r				• dr )				(7)
S , = Р • 4 α	( 1 -	cos ( 4an			)) J ( S p ( r ) • dr >>					(8)
S r = ПР J ( S T ( r ) • dr ) .					r					(9)

Эти величины не зависят от ϕ, z и это соответствует закону сохранения энергии.

Полный поток энергии равен мощности P , передаваемой по проводу, т.е.

Sz = P,( где

Г,)

P = Rh J J J2dp dr = 4nR2RJo , r V ФV

где R_H - сопротивление нагрузки.

Пример 3. При условиях примера 1 и удельном сопротивлении медного провода p = 0.0175 -10 6 найдена величина потока энергии Sz «1000. Равная ему мощность P ~ 1000 потребляется в сопротивлении RH ~ 110 при плотности основного 98

тока J o = 10 6 . Важно отметить, что поток энергии вдоль провода значительно превышает потоки энергии по радиусу и по окружности. В данном примере S z = 1000, S r = - 10 -5 , S ^ = - 5 - 10 — ⁷ .

Пример 4.

В условиях примера 3 будем изменять одну из величин α , χ , оставляя другую неизменной. В табл. 1 показаны значения величин α , χ и мощности Р, а на рис. 5 показаны соответствующие графики

Таблица 1.

Вариант	α 0.1 α	X - 4 - 10 11	Р
41	1	1	1000
43	1	0.8	830
44	1	1.2	1240
45	1.5	1	1300
46	0.5	1	580

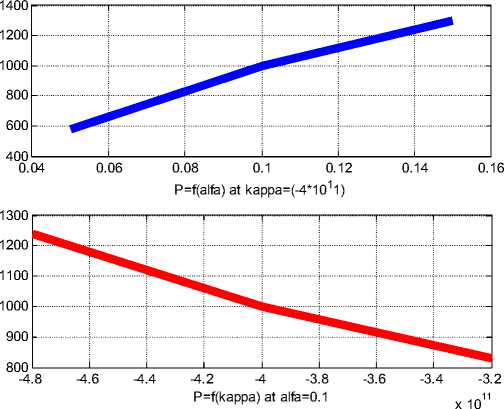
Рис. 5.

Обсуждение

Итак, поток энергии вдоль оси провода Sz создается токами и напряженностями, направленными по радиусу и окружности. Этот поток энергии равен мощности, выделяемой в нагрузке RH и в сопротивлении провода. Токи, текущие вдоль радиуса и окружности, также создают тепловые потери. Их мощность равна потокам энергии Sr, Sф, направленным по радиусу и окружности.

Вопрос о том, каким образом поток электромагнитной энергии создает электрический ток, рассматривается в [8]. Там показано, что существует четвертая электромагнитная индукция, создаваемая изменением потока электромагнитной энергии. Затем находится зависимость э.д.с. этой индукции от плотности потока электромагнитной энергии и параметров провода.

Показано, что постоянный ток в проводе имеет сложную структуру и распространяется внутри провода по спирали. При постоянной величине тока плотность спиральной траектории уменьшается по мере уменьшения оставшегося сопротивления нагрузки. Имеется две составляющие тока. Плотность первой составляющей J_o постоянна на всем сечении провода. Плотность второй составляющей изменяется по сечению провода таким образом, что ток распространяется по спирали. В цилиндрических координатах r , ф , z эта вторая плотность имеет три компоненты J_r, J _ф , J_z . Они могут быть найдены как решение уравнений Максвелла.

Известен эксперимент, который может служить экспериментальным доказательством существования указанной структуры постоянного тока.

При неизменной плотности основного тока в проводе передаваемая по нему мощность зависит от параметров структуры ( α , χ ), которые влияют на плотность витков спиральной траектории тока. Таким образом, один и тот же ток в данном проводе может передавать различную мощность (зависящую от нагрузки).

Снова рассмотрим рис. 1. На участке AB по проводу передается энергия нагрузки P. Ей соответствует определенное значение параметров структуры ( α , χ ) и, как следствие, плотность витков спиральной траектории тока. На участке CD по проводу передается незначительная энергия. Ей соответствует малая плотность витков спиральной траектории тока.

Естественно, нагрузкой является и сопротивление самого провода. Следовательно, по мере прохождения тока по проводу спираль траектории тока выпрямляется.

Зависимость плотностей токов и напряженностей от переменной ϕ подробно рассмотрена в [2]. Вообще, предложенную в [2] математическую модель можно рассматривать как следствие данной модели при X ^ 0 •

Таким образом, показано, что существует такое решение уравнений Максвелла для провода с постоянным током, которому соответствует представление о

• •    законе сохранения энергии,

• •    спиральной траектории постоянного тока в проводе,

• •    передаче энергии вдоль и внутри провода,

• •    зависимости плотности спиральной траектории от передаваемой мощности.

Приложение 1.

Рассматривается решение уравнений (2.5-2.9) в виде функций (2.10-2.17). Далее производные по r будем обозначать штрихами. Перепишем уравнения (2.5-2.9) в виде

• j r^r)- + j‘ (r) + jr a + X-j. (r) = 0,

rr

• h r^r) + h^ (r)+ M—L a + X-hz (r) = 0,(2)

rr

• Г    ■ hz (r)« — hp (r- X = jr (r j

• —    hr (r )X — hZ (r- = jp(rX

• h ^-) + hp(r - + hrr •a — jz (r - = 0

rr

Умножим (5) на ( — x ) - Тогда получим:

• —    X hp(.r- -x-hp (r- - X hr(rj• a + x-jz(r- = 0,

rr

Сравнивая (1) и (6), замечаем, что они совпадают, если — hp(r - X = jr (r ^,

• —    hr(r JX = jp( r - •(8)

Важно отметить, что такое сравнение справедливо только при j_z ( r ) ^ 0. Уравнения (7, 8) совпадают с (3, 4) при h_z ( r ) = 0 • Следовательно, при j_z ( r ) ^ 0 и h_z ( r ) = 0 уравнение (1) может быть исключено и система уравнений (1-5) упрощается и принимает вид

hA. ' + hr ( r ) + h p < r > a = 0 , rr	(9)
- h p ( r ) X = L ( r J,	(10)
- h r ( r . X = j p ( r ) ,	(11)
h. Jr r )              1 + h ‘ ( r ) + • h r ( r ) a = j z ( r ) • rr	(12)
Рассмотрим теперь случай, когда jz ( r ) = 0 •	При этом исходная
система примет вид:
jr ^ r ) + jr ( r ) + j ^ r ) a = 0 , rr	(13)
hr ^ r . + hr ( r ) + ^p ( r ) a + X" hz ( r ) = 0 , rr	(14)
1 • h z ( Г ) a - h p ( r ) X = j r ( r ) , r	(15)
- h r ( r ) X - h z ( r ) = j p ( r X	(16)
p    + h z ( r ) + • h r ( r ^a = 0 • rr	(17)
Подставим (15, 16) в (13). Тогда получим:

"Г • hz (r)a - - • hp(r)x +- " hz(r)a - h'(p(r)X - (h(r)X + hz(r))a = 0 r   rr         r или

• - *2 • hz (r)a - * • hp(r)x - hP (r)X - hr(r )— = 0

rrr

При этом для вычисления трех напряженностей получим три уравнения (14, 17, 18). Исключим h ‘ ( r ) из (17, 18):

• 1           1         .I Ij/x \a I

— • hz (r)ahp (r) X +1 -• hp (r) + hr (r )— IX - hr (r

• r              r             v r                 r )

или

• -* 2 • h_z ( r ) a = 0 . r

Таким образом, и при j_z ( r ) = 0 должно соблюдаться условие h_z ( r ) = 0 . Итак, система уравнений (9-12) выполняется при любом j z ^{( r} ) •

Приложение 2.

В разделе 3 показано, что потоки энергии в сечении провода,

S =

S

S

S

r

ϕ

^S_r ^{( r} ) • si ²

= p JJJ S _v ( r ) • si • co dir • dv • dz .

r ,V,z

z

S_z ( r ) • si • co

В точке z=0 оси oz, учитывая (2.10, 2.11), имеем:

S =

S

S

S

r

ϕ

^S r ^{( r} ) • ^sin2 ^{( д}ф )

= P JJ S v ( r ) • ( - sin ( дф ) • cos ( av )) dr • dv

r ,V

z

S z ( r ) • ( - sin ( av ) • cos ( av ))

.

Рассмотрим вначале поток

S z = p Jf £ ( r ) • ( - sin ( gv ) cos ( gvHr • dv )

r ,ф или

A

A

Sz =

-

^p J S . ⁽ r ) • J . _;Я 2^дг 1 dv dr

r

V V ф

7 7

или sz = p •(I z 4a v

Аналогично,

Sv = P •( 4a

- cos(4an))J

r

- cos

r

^S r = ⁿP J ( ^ r ^{( r} ) • ^dr )•

r

Очевидно, при любом выборе точки z=0 на оси oz последнее соотношение сохраняется.