Вторичная потеря устойчивости круглой пластины при нагреве
Автор: Левяков С.В.
Статья в выпуске: 4, 2022 года.
Бесплатный доступ
Потеря устойчивости плоской формы равновесия круглой пластины с неподвижным краем при нагреве сопровождается переходом к осесимметричному изогнутому состоянию равновесия. Прогрессирующий изгиб при возрастающей температурной нагрузке в закритической области приводит к существенному изменению напряженного состояния пластины и появлению высоких сжимающих окружных напряжений в кольцевой области, примыкающей к краю. При этом становится возможной вторичная потеря устойчивости, связанная с нарушением осесимметричности напряженно-деформированного состояния. В данной работе рассматривается задача об устойчивости закритических осесимметричных форм равновесия круглой пластины при нагреве. Кроме ограничений, налагаемых на радиальное смещение и прогиб в граничных точках пластины, вводится угловая связь с конечной жесткостью, варьирование которой позволяет моделировать граничные условия в диапазоне от шарнирного закрепления до заделки. Для решения задачи используется полуаналитический метод конечных элементов, основанный на аппроксимации перемещений отрезками тригонометрических рядов Фурье по окружной координате. При выводе основных соотношений нелинейность деформирования учитывается в квадратичном приближении, соответствующем теории гибких пластин Фёппля - Кармана. Для отыскания равновесных состояний пластины сформулирован итерационный алгоритм, основанный на вычислении коэффициентов первой и второй вариаций полной потенциальной энергии пластины. Анализ устойчивости найденных состояний равновесия проводится с использованием критерия положительной определенности матрицы Гессе для конечно-элементной модели пластины. Определены значения температур, при которых происходит вторичная потеря устойчивости пластины, означающая переход к смежным несимметричным формам равновесия. Исследовано закритическое деформирование пластины, характеризуемое появлением и развитием локальных складок вблизи граничного контура. Изучено влияние граничных условий и физико-механических свойств материала на критическое значение температурной нагрузки и форму вторичной потери устойчивости. .
Круглая пластина, нелинейный изгиб, большие прогибы, устойчивость, вторичное выпучивание, полуаналитический метод конечных элементов
Короткий адрес: https://sciup.org/146282588
IDR: 146282588 | УДК: 539.3 | DOI: 10.15593/perm.mech/2022.4.03
Текст научной статьи Вторичная потеря устойчивости круглой пластины при нагреве
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2022PNRPU MECHANICS BULLETIN
Расчеты на устойчивость являются важной частью комплекса механических расчетов конструкций, включающих в себя тонкостенные элементы в виде пластин и оболочек. Целью расчетов является определение критических нагрузок таких элементов и в случае необходимости выработка рекомендаций по их усилению. Однако известно, что во многих практических ситуациях пластины и пологие панели сохраняют способность воспринимать возрастающую нагрузку и после потери устойчивости [1]. Поэтому теоретический и практический интерес представляет исследование нелинейного напряженно-деформированного состояния пластин и оболочек в закритической области, где упругие прогибы могут значительно превышать их толщину.
Задача о выпучивании гибкой круглой пластины при радиальном сжатии относится к числу классических задач теории устойчивости упругих конструкций. Ее аналитическое решение, выраженное в функциях Бесселя [1; 2], позволяет вычислить критические значения нагрузки для различных условий опирания граничного контура. Изучению нелинейного осесимметричного изгиба сжимаемой пластины в закритической области посвящены работы [3–10]. Установлено, что при радиальной нагрузке, значительно превышающей критическое значение, центральная часть пластины уплощается, а изгибные деформации концентрируются в узкой кольцевой области, примыкающей к границе. При возрастании внешней радиальной нагрузки ок- ружные напряжения вблизи границы меняют знак и становятся сжимающими, достигая значительного уровня. В [3] впервые высказано предположение о возможности вторичного выпучивания, связанного с переходом к неосесимметричным формам равновесия. В [11] на основе асимптотических формул для перемещений показано, что при радиальных нагрузках, превышающих критическое значение, возможны устойчивые неосесимметричные формы равновесия. Данные выводы нашли подтверждение в работах [12; 13], где для жестко защемленной круглой пластины методом конечных разностей вычислены критические нагрузки и соответствующие неосесимметричные формы вторичной потери устойчивости. В [14] предпринята попытка построения более полного нелинейного решения, описывающего поведение сжатой пластины после вторичного выпучивания. С этой целью использовано разложение неизвестных функций в степенные ряды по радиальной координате и ряды Фурье по окружной координате. Получены весьма громоздкие соотношения, использование которых в практических расчетах вызывает значительные трудности.
Отметим, что несимметричное выпучивание круглых пластин, связанное с появлением локальных складок вблизи закрепленного края, наблюдается также при действии поперечных механических нагрузок [15–19].
Обзор литературы показывает, что задачи об устойчивости и закритическом деформировании круглых пластин при нагреве рассматривались в основном в осесимметричной постановке. Так, в [20] изучено нелинейное деформирование неравномерно нагретых пластин с использованием уравнений, основанных на допущении о пренебрежимо малом влиянии второго инварианта деформаций. Нелинейные конечноэлементные формулировки для исследования закрити-ческого изгиба тонких пластин при различных граничных условиях даны в [21; 22]. Упрощенный метод для расчета зависимости температурной нагрузки от прогиба пластины предложен в [23]. В работах [24; 25] изучено влияние осесимметричных начальных неправильностей формы на нелинейный изгиб пластин, изготовленных из градиентных материалов. Термоупругий закритический изгиб пластин при наличии упругих связей, ограничивающих радиальные перемещения края, исследован в [26].
Вопрос о существовании несимметричных форм равновесия круглых пластин после потери устойчивости при нагреве исследован недостаточно. Отметим работу [27], в которой экспериментально изучено несимметричное выпучивание круглых пластин и предложена приближенная формула для оценки критической сжимающей нагрузки в зависимости от числа волн формы выпучивания. С использованием численно-аналитического метода, основанного на применении степенных рядов, в [28; 29] исследована возможность вторичной потери устойчивости нагретых круглых пластин из градиентных материалов при различных условиях опирания края. Установлено, что при смягчении граничных условий критическая температура резко возрастает. Отмечается значительное снижение скорости сходимости решения в области больших температурных прогибов, где происходит вторичное выпучивание.
Изучение дальнейшего закритического деформирования нагретых круглых пластин методом степенных рядов вызывает значительные трудности, связанные как с громоздкими выражениями, так и с медленной сходимостью рядов. Преодоление указанных трудностей возможно с использованием метода конечных элементов. В связи с этим необходимо отметить, что применение оболочечных элементов общего назначения требует значительных затрат времени и ресурсов ЭВМ, так как для определения резко изменяющегося нелинейного напряженно-деформированного состояния вблизи края пластины необходимо измельчение сетки по двум координатным направлениям. При этом увеличение общего числа степеней свободы конечно-элементной модели приводит к резкому возрастанию объема вычислений, так как для отыскания равновесных состояний необходимо использовать пошаговую схему увеличения нагрузки в сочетании с итерационными методами уточнения нелинейного решения на каждом шаге.
Учитывая специфику рассматриваемой задачи, в настоящей работе предлагается использовать полуанали-тический вариант метода конечных элементов, основанный на представлении неизвестных функций отрезками рядов Фурье по окружной координате. Выбранный подход позволяет снизить общее число степеней свобо- ды дискретной модели пластины и точно описать характер изменения перемещений по окружной координате в момент потери устойчивости.
1. Основные соотношения
Рассмотрим круглую пластину радиуса а , отнесенную к цилиндрической системе координат r , θ , z . Пластина подвергается воздействию стационарного температурного поля, не зависящего от окружной координаты θ . На граничном контуре r = a установлены жесткие связи, исключающие смещение точек срединной поверхности в радиальном и поперечном направлениях. На углы поворота в радиальном направлении налагаются упругие связи с заданной угловой жесткостью. Изменение жесткости связи позволяет моделировать граничные условия в диапазоне от жесткой заделки до шарнирного опирания.
Пластина изготовлена из линейно упругого изотропного материала, подчиняющегося закону Гука. Учитывается зависимость физико-механических свойств материала от температуры.
Для исследования нелинейного деформирования и устойчивости пластины при нагреве используем деформационные соотношения, соответствующие теории гибких пластин Фёппля – Кармана [1]
-
ε 11 = u , r + 1 2 w , r 2 , ε 22 = 1 ru + 1 rv , θ+ 2 1 r 2 w , θ 2 ,
ε 12 = r 1 u , θ- 1 rv + v , r + 1 rw , rw , θ , (1)
κ 11 = - w , rr , κ 22 =- 1 r ( w , r + 1 rw , θθ ),
κ 12 =- 1 r w , r θ + r 1 2 w , θ , (2)
где u , v , w – перемещения срединной поверхности пластины в радиальном, окружном и поперечном направлениях соответственно; ε 11 , ε 22 , ε 12 – деформации; κ 11 , κ 22 , κ 12 – кривизны срединной поверхности; индексом после запятой обозначены частные производные по соответствующей координате.
Введем следующие обозначения:
h /2
( B , D ) = (1, z 2) E dz ,
-
- h /2 1 -ν 2
h /2 E αΔ T
( NT , MT ) = (1, z ) dz ,
- h /2 1 -ν
Is = s 11 + s 22 ,
ss = s 11 s 22 - 4 s 12 ,
где E , ν – модуль Юнга и коэффициент Пуассона соответственно; α – коэффициент линейного расширения материала; Δ T – изменение температуры (температурная нагрузка); B , D – упругие постоянные материала; NT , MT – температурные силы и моменты соответственно; Is , I ss – инварианты тензора sij ( i , j = 1, 2).
Используя обозначения (3) и (4), запишем полную потенциальную энергию нагретой пластины с упруго защемленным краем
Π= 1 B ∫∫ { I ε 2 - 2(1 -ν ) I εε } rdrd θ+
2 A
+ 1 D ∫∫ { I κ 2 - 2(1 -ν ) I κκ } rdrd θ- 2 A
2 π
- ∫∫ ( N T I ε + M T I κ ) rdrd θ+ 1 ac ϕ ∫ ( w , r r = a )2 d θ , (5)
A 2 0
где А – площадь срединной поверхности пластины; c ϕ – угловая жесткость; I ε , I εε , I κ , I κκ – инварианты тензоров деформации и кривизны срединной поверхности, которые определяются формулами (4).
-
2. Формулировка конечного элемента
Представим пластину как набор n кольцевых конечных элементов с узловыми окружностями радиуса rj (j = 0,1,... n ). Перемещения в пределах каждого элемента представим в виде отрезков рядов Фурье по окружной координате u=u0+ukcoskθ+u2kcos2kθ, v=vksinkθ+v2ksin2kθ, (6)
w=w0+wkcoskθ+w2kcos2kθ, где u0 , uk , …, w2k – функции радиальной координаты; k – число волн по окружной координате.
Для аппроксимации перемещений в плоскости пластины используем линейные функции формы, а для аппроксимации прогибов – кубические функции формы us=us1L1(x)+us2L2(x) (s=0,k,2k),(7)
vs=vs1L1(x)+vs2L2(x) (s=k,2k),(8)
ws = ws 1 N 1( x ) +ϕ s 1 N 2( x ) + ws 2 N 3( x ) +ϕ s 2 N 4( x )
(s = 0, k, 2k),(9)
L1(x)=1-x/l, L2(x)= x/l,(10)
N 1( x ) = 1 - 3( x / l )2 + 2( x / l )3,
N2(x)=x-2x2/l+x3/l2,(11)
N 3( x ) = 3( x / l )2 - 2( x / l )3,
N4(x)=x3/l2-x2/l, где х – локальная радиальная координата (0 ≤ x ≤ l); l=r2-r1 – ширина кольцевого конечного элемента; r1 , r2 – внутренний и внешний радиусы элемента соответ- ственно; usi , vsi , wsi – узловые перемещения; ϕsi – узловые углы поворота (i = 1,2 ).
Как следует из принятой аппроксимации перемещений, деформированное состояние конечного элемента описывается 22 обобщенными координатами (степенями свободы), которые образуют вектор qT=(q1T,q2T), qiT =(u0i,w0i,ϕ0i,uki,vki,wki,ϕki,u2ki,v2ki,w2ki,ϕ2ki)
( i = 1,2), (12)
где i – номер узловой окружности элемента.
Подставляя (1), (2) и (4) в (5) и учитывая принятые аппроксимации для перемещений (6)–(11), получим потенциальную энергию элемента в виде функции обобщенных координат (12). Интегрирование по окружной координате в формуле (5) выполняется в аналитическом виде. При вычислении интегралов по радиальной координате переменные коэффициенты в соотношениях (1) и (2), зависящие от радиальной координаты, заменяются их средними значениями по элементу и применяются квадратурные формулы Гаусса по семи точкам.
Используя принцип стационарности полной потенциальной энергии конечно-элементной модели пластины, получим условия равновесия в виде системы нелинейных алгебраических уравнений относительно узловых неизвестных. Задавая пошаговое увеличение температурной нагрузки, на каждом шаге отыскиваем решение системы уравнений с помощью итерационной процедуры Ньютона – Рафсона по схеме
H m - 1 δ q m + g m - 1 = 0, (13)
qm=qm-1 +δqm, где g и H – градиент и матрица Гессе, определяющие первую и вторую вариации полной потенциальной энергии пластины; δq – вектор поправок к решению;
m – номер итерации.
Решение вопроса об устойчивости найденных равновесных состояний пластины связано с исследованием положительной определенности второй вариации полной потенциальной энергии. В соответствии с критерием Сильвестра вторая вариация энергии положительно определена, и соответствующее состояние равновесия устойчиво, если все угловые миноры матрицы Гессе положительны. Проверка этого условия легко выполняется после приведения матрицы к треугольному виду при решении системы (13) методом Гаусса. Смена знака хотя бы одного минора свидетельствует о достижении критического состояния.
В рассматриваемом случае потеря устойчивости пластины происходит при прохождении через точку бифуркации. Для перехода на новую ветвь решения вычисляется форма потери устойчивости ϕ как нетриви- альное решение системы Hф = 0 для критического состояния, где det H = 0. Вычисленная форма используется в качестве начального приближения для отыскания смежной формы равновесия.
3. Численные результаты
Приводимые ниже результаты получены для пластины из нержавеющей стали, физико-механические свойства которой зависят от температуры согласно степенному закону [30]:
P = P 0(1 + P 1 T + P 2 T 2 ), (14)
где P – свойство материала, например, модуль упругости, коэффициент линейного расширения и т.д.; P 0, P 1, P 2 – коэффициенты, приведенные в табл. 1; Т – текущая температура.
Для проверки и оценки эффективности разработанной конечно-элементной модели рассмотрим задачу о нелинейном деформировании и вторичной потери устойчивости круглой жестко защемленной пластины при равномерном нагреве. Радиус пластины a = 0,1 м, толщина h = 0,001 м. Расчеты проведены в предположении, что свойства материала не зависят от температуры и соответствуют значению T 0 = 300 К. В табл. 2 приведены значения критической температурной нагрузки A T r. 2 = T cr 2 — T 0 в зависимости от числа конечных элементов N для различного числа волн k по окружной координате. Рассматриваемое решение хорошо согласуется с результатами, полученными с помощью степенных рядов [29]. Относительная разница сравниваемых решений не превосходит 5 % при использовании 100 конечных элементов.
Для исследования влияния температурно-зависимых свойств материала на устойчивость защемленной пластины проведены расчеты для указанных выше размеров пластины при использовании 400 конечных элементов. Рассмотрены два типа граничных условий: жесткая заделка, при которой все перемещения и углы поворота на краю пластины равны нулю, и скользящая заделка, которая, в отличие от жесткой заделки, допускает перемещения точек граничного контура в окружном направлении. Результаты вычислений критических температурных нагрузок A T cr 1 и A T cr 2, при которых происходит первичная (осесимметричная) и вторичная (несимметричная) потеря устойчивости, приведены в табл. 3. Сокращения ТН и ТЗ относятся к свойствам материала, не зависящим и зависящим от текущей температуры соответственно.
На рис. 1 показана типичная диаграмма деформирования, показывающая нелинейную зависимость температурной нагрузки от прогиба в центре пластины. Сплошные линии соответствуют жесткой заделке, а пунктирные линии – шарнирно опертому краю. Кружками отмечены точки бифуркации нелинейного решения.
Таблица 1/Table 1
Коэффициенты, определяющие свойства материала
Coefficients determining material properties
|
Характеристика |
Размерность |
P 0 |
P 1 |
P 2 |
|
E |
Па |
201,04 x 10 9 |
3,079 x 10-4 |
-6,534 x 10-7 |
|
V |
0,3262 |
-2,002 x 10-4 |
3,797 x 10-7 |
|
|
a |
K–1 |
12,33 x 10-6 |
8,086 x 10-4 |
0 |
Таблица 2/Table 2
Критическая нагрузка A T cr 2, К для жестко защемленной пластины
Critical temperature rise A T cr 2 in K for the clamped plate
|
k |
Рассматриваемое решение |
Решение [29] |
|||
|
N = 50 |
N = 100 |
N = 200 |
N = 400 |
||
|
7 |
311,01 |
333,14 |
341,63 |
344,11 |
345,0 |
|
8 |
311,40 |
323,76 |
327,74 |
328,82 |
329,2 |
|
9 |
332,49 |
343,86 |
347,47 |
348,44 |
348,8 |
Таблица 3/Table 3
Влияние граничных условий и свойств материала на критическую температурную нагрузку
The effect of the boundary conditions and material properties on the critical temperature rise
|
Граничные условия |
Свойства материала |
cr 1 , K |
^ T cr 2 , K |
|||
|
k = 7 |
k = 8 |
k = 9 |
k = 10 |
|||
|
u = v = w = w , r = 0 |
ТН |
6,06 |
344,11 |
328,82 |
348,44 |
378,48 |
|
ТЗ |
6,04 |
290,04 |
279,45 |
294,10 |
316,08 |
|
|
u = w = w , r = 0 |
ТН |
6,06 |
322,34 |
324,94 |
347,47 |
378,34 |
|
ТЗ |
6,04 |
274,82 |
276,79 |
293,50 |
316,01 |
|
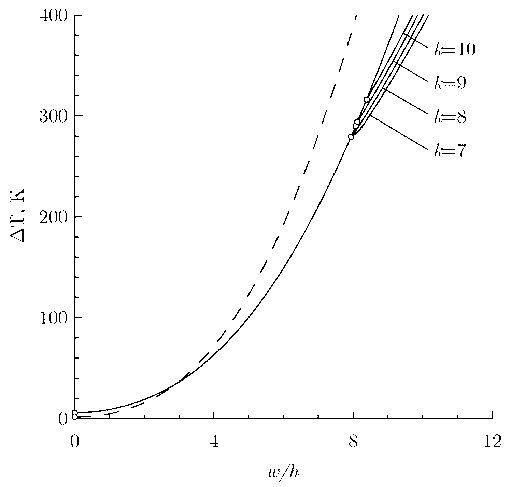
Рис. 1. Зависимость температурной нагрузки от центрального прогиба защемленной пластины
Fig. 1. Temperature rise versus central deflection of the clamped plate
Как видно из приведенных данных, первичное (осесимметричное) выпучивание происходит при незначительном нагреве, а вторичное (несимметричное) выпучивание пластины наблюдается в области высоких температур, где становятся заметными изменения свойств материала. Допущение о независимости свойств материала от температуры приводит к завышению критической температурной нагрузки приблизительно на 18 %. Для скользящей заделки, допускающей перемещения точек граничного контура в окружном направлении, критическая нагрузка несимметричного выпучивания с минимальным числом окружных волн k = 7 снижается незначительно (на 5 %). При увеличении k различие в результатах для жесткой и скользящей заделки быстро уменьшается. При анализе устойчивости осесимметричного изгиба шарнирно опертой пластины критические состояния не обнаружены.
При температурных нагрузках, значительно превышающих критическое значение, центральная часть пластины уплощается, а изгиб происходит в кольцевой зоне, примыкающей к границе. При этом прогибы в центре пластины превышают ее толщину и в момент вторичной потери устойчивости составляют w max ≈ 8 h .
Исследуем влияние упругой связи, налагаемой на поворот граничного контура, на критическую нагрузку и форму вторичного выпучивания пластины. При этом учитываем зависимость свойств материала от температуры согласно закону (14). В табл. 4 представлены результаты расчетов для различных значений параметра упругой связи γ= c ϕ a / D для двух типов граничных условий. При больших значениях параметра γ> 100 критическая нагрузка стремится к значению, вычисленному для жестко защемленного края. С уменьшением γ критическая нагрузка вторичного выпучивания возрастает, при этом увеличивается число окружных волн соответствующей формы выпучивания. При значениях параметра γ , приближающихся к нулю (предельный случай шарнирно опертого края), критическая температурная нагрузка неограниченно возрастает. Это значит, что устойчивость осесимметричной формы равновесия шарнирно опертой пластины сохраняется при возрастании температурной нагрузки.
В качестве характеристики напряженного состояния пластины рассмотрим радиальное давление на контуре σ 0 , которое вычислим как среднее значение реакции по направлению радиальной связи
-
1 ∂Π σ 0 = ,
2 π ah ∂ u 0 ( a )
где П – полная потенциальная энергия конечно-элементной модели пластины. На рис. 2 показана зависимость безразмерного давления от температурной на- грузки для различных значений параметра угловой связи на контуре. Штрихпунктирная линия отвечает линейному решению задачи. Точки бифуркации и соответствующие ветви нелинейного решения отвечают минимальной критической температурной нагрузке (см. табл. 4). Для осесимметричного выпучивания жестко защемленной пластины получаем известный результат σ0 =14,682D/(a2h) [1; 2]. Значение радиального давления при вторичном выпучивании превышает это значение приблизительно в 10 раз.
Деформирование после вторичной потери устойчивости характеризуется увеличением амплитуды складок. Формы равновесия пластины в закритической области деформирования показаны на рис. 3 в реальном масштабе.
Таблица 4/Table 4
Критическая нагрузка Δ Tcr 2 , К для упруго защемленной пластины
Critical temperature rise Δ Tcr 2 , К for the plate with rotationally restrained edge
|
γ |
Граничные условия |
|
|
u = v = w = 0 |
u = w = 0 |
|
|
100 |
280,1 ( k = 8) |
274,4 ( k = 7) |
|
20 |
286,4 ( k = 8) |
277,7 ( k = 7) |
|
10 |
309,2 ( k = 8) |
291,8 ( k = 8) |
|
8 |
327,0 ( k = 9) |
303,8 ( k = 8) |
|
6 |
369,2 ( k = 9) |
340,9 ( k = 9) |
|
4 |
496,6 ( k = 12) |
458,2 ( k = 11) |
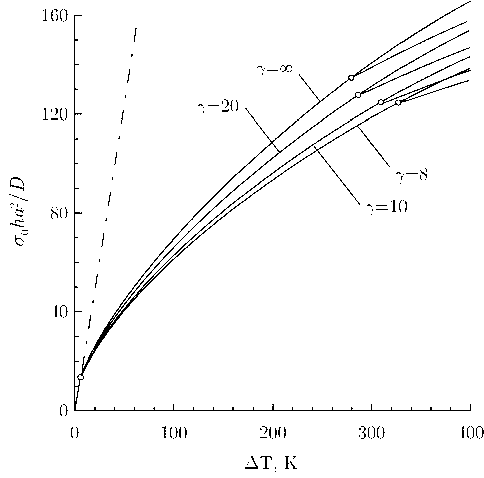
Рис. 2. Зависимость среднего радиального давления от температурной нагрузки упруго защемленной пластины
Fig. 2. Averaged radial pressure versus temperature rise of the plate with rotationally restrained edge

а
b
Рис. 3 Формы равновесия пластины после вторичного выпучивания:
а ) Y= ^ ; k = 8; а т = 313 K w / h = 8,6 ; b ) y = 4; k = 12; A T = 513 K; w / h = 10,48
Fig. 3 Equilibrium states of the plate after secondary buckling:
а ) у = ^ ; k = 8; A T = 313 K; w / h = 8,6 ; b ) y = 4; k = 12; A T = 513 K; w / h = 10,48
Заключение
Представлены результаты численного исследования устойчивости осесимметричной формы упругого равновесия, которую принимает круглая пластина с неподвижным краем после выпучивания при нагреве. Показано, что при дальнейшем возрастании температуры возможна вторичная потеря устойчивости, которая нарушает симметрию и приводит к образованию локальных складок
Список литературы Вторичная потеря устойчивости круглой пластины при нагреве
- Вольмир А.С. Устойчивость деформируемых систем. -М.: Наука, 1967. - 984 с.
- Wang C.M., Wang C.Y., Reddy J.N. Exact solutions for buckling of structural members. - CRC Press, 2005. - 224 p.
- Friedrichs K.O., Stoker J.J. The non-linear boundary value problem of the buckled plate // Proc. NAS. - 1939. -Vol. 25. - P. 535-540.
- Bodner S.R. The post buckling behavior of a clamped circular plate // Quart. Appl. Math. - 1955. - Vol. 12, no. 4. - P. 397-401.
- Weinberg I.J. Symmetric finite deflections of circular plates subjected to compressive edge forces // Studies in Applied Mathematics. - 1962. - Vol. 41, no. 1-4. - P. 104-115.
- Keller H.B., Reiss E.L. Non-linear Bending and Buckling of Circular Plates // Proc. 3rd U.S. Nat. Cong. of Appl. Math. -1958. - P. 375-385.
- Rao G.V., K.K. Raju. A reinvestigation of post-buckling behaviour of elastic circular plates using a simple finite element formulation // Compu. Struct. - 1983. - Vol. 17, no. 2. - P. 233-235. DOI: 10.1016/0045-7949(83)90011-1.
- Ye J.Q. Axisymmetric elastic postbuckling of circular plates // Int. J. Pres. Ves. Piping. - 1995. - Vol. 62, no. 3. - P. 213-217. DOI: 10.1016/0308-0161 (94)00014-A.
- Tanaka M., Matsumoto T., Zheng Z. Application of the boundary-domain element method to the pre/post-buckling problem of von Karman plates // Engineering Analysis with Boundary Elements. - 1999. - Vol. 23, no. 5-6. - P. 399-404. DOI: 10.1016/S0955-7997(98)00102-7.
- Yanowitch M. Non-linear buckling of circular elastic plates // Comm. on Pure and Appl. Math. - 1956. - Vol. 9. -P. 661-672.
- Морозов Н.Ф. Исследование круглой симметрично сжимаемой пластинки при большой краевой нагрузке // Изв. вузов. - 1963. - Т. 34, № 3. - С. 95-98.
- Cheo L.S., Reiss E.L. Unsymmetric wrinkling of circular plates // Quart. App. Math. - 1973. - Vol. 31. - P. 75-91.
- Cheo L.S., Reiss E.L. Secondary buckling of circular plates // SIAM J. Appl. Math. - 1974. - Vol. 26, no. 3. - P. 490-495.
- Wang A. Axisymmetric postbuckling and secondary bifurcation buckling of circular plates // Int. J. Non-Linear Mech. - 2000. - Vol. 35, no. 2. - P. 279-292. doi.org/10.1016/S0020-7462(99)00014-1.
- Панов Д.Ю., Феодосьев В.И. О равновесии и потере устойчивости пологих оболочек при больших прогибах // ПММ. - 1948. - Т. 12, № 4. - C. 389-406.
- Adams G.G. Elastic wrinkling of a tensioned circular plate using von Karman plate theory // ASME J. Appl. Mech. -1993. - Vol. 60, no. 2. - P. 520-525. DOI: 10.1115/1.2900824.
- Бауэр С.М., Воронкова Е.Б., Романова А.А. О потере устойчивости осесимметричных форм равновесия круглых пластин под действием нормального давления // Вестник СПбГУ. Сер. 1. - 2012. - Вып. 1. - С. 80-85.
- Coman C.D. Asymmetric bifurcations in a pressurised circular thin plate under initial tension // Mech. Res. Commun. - 2013. - No. 47. - P. 11-17. DOI: 10.1016/j.mechrescom.2012.09.005.
- Coman C.D., Bassom A.P. On the nonlinear membrane approximation and edge-wrinkling // Int. J. Solids Struct. - 2016. -Vol. 82. - P. 85-94. DOI: 10.1016/j.ijsolstr.2015.11.011.
- Pal M.C. Large deflections of heated circular plates // Acta Mechanica. - 1969. - Vol. 8. - P. 82-103.
- Raju K.K., Rao G.V. Thermal post-buckling of circular plates // Comput. Struct. - 1984. - Vol. 18, no. 6. -P. 1179-1182.
- Rao G.V., Raju K.K., Naidu N.R. Post-buckling behavior of circular plates with elastically restrained edges subjected to thermal loads // Comput. Struct. - 1992. - Vol. 45, no. 1. - P. 209-210.
- Varma R.R., Rao G.V. Novel formulation to study thermal postbuckling of circular plates with edges elastically restrained against rotation // J. Eng. Mech. - 2011. - Vol. 137, no. 10. - P. 708-711. DOI: 10.1061/(ASCE)EM.1943-7889.0000274.
- Li S.R., Zhang J.H., Zhao Y.G. Nonlinear thermome-chanical post-buckling of circular FGM plate with geometric imperfection // Thin-Walled Structures. - 2007. - Vol. 45, no. 5. -P. 528-536. DOI: 10.1016/j.tws.2007.04.002.
- Kiani Y., Eslami M.R. Thermal postbuckling of imperfect circular functionally graded material plates: Examination of Voigt, Mori-Tanaka and self-consistent schemes // J. Press. Vessel Technol. - 2015. - Vol. 137, no. 2. - P. 1-11. DOI: 10.1115/1.4026993.
- Sun Y., Wang M.L., Li S.R. Thermal buckling and post-buckling of FGM circular plates with in-plane elastic restraints // Appl. Math. Mech. - 2017. - Vol. 38, no. 10. - P. 1459-1470. DOI: 10.1007/s10483-017-2242-6.
- Гольдштейн Р.В., Попов А.Л., Козинцев В.М., Че-любеев Д.А., Неосесимметричная потеря устойчивости при осесимметричном нагреве круглой пластины, Вестник ПНИПУ. Механика. - 2016. - № 2. - С. 45-53. DOI: 10.15593/ perm.mech/2016.2.04.
- Levyakov S.V. Wrinkling of pressurized circular functionally graded plates under thermal loading // Thin-Walled Structures. -2019. - Vol. 137. - P. 284-294. DOI: 10.1016/j.tws.2018.11.029.
- Levyakov S.V. Asymmetric thermal buckling of imperfect FGM circular plates with rotationally restrained edge // Int. J. Struct. Stability and Dynamics. - 2020. - Vol. 20, no. 12.
- Shen H.S. Functionally Graded Materials: Nonlinear Analysis of Plates and Shells. - CRC Press, Boca Raton, FL, USA, 2009. - 266 p.


