Вторичное уплотнение дискретных последовательностей на основе бинарных функциональных преобразований

Некоторым альтернативным способом увеличения информационного содержания в сообщениях может стать использование методов вторичного уплотнения каналов. Суть вторичного уплотнения заключается в объединении неортогональных в гильбертовой метрике сигналов. Вторичное уплотнение приводит к взаимному искажению уплотняемых сигналов. С целью придания сигналам некоторой иерархии (по их значимости в рамках информационого содержания) вводятся понятия, разделяющие сигналы на основной и вторичный. Основной сигнал предназначен для передачи сообщений, характеризуемых значительной информационной емкостью (видео-, аудиосигналов и т.д.). Вторичный сигнал (по сути являющийся шумовым) может предназначаться для передачи сопутствующих сообщений меньшего информационного объема (сигналы сигнализации, верификации, управления и т.д.) в незаметном (скрытом) для абонентов режиме.

Помимо непрерывных способов вторичного уплотнения [1-3] интерес представляет организация вторичного каналообразования для дискретных последовательностей в цифровых телекоммуникационных системах (ТС). В связи с тем, что подобные задачи вторичного уплотнения могут решаться неоднозначным способом, предлагается один из возможных способов их решения.

Постановка задачи

Концептуальная задача вторичного уплотне-ниядискретныхпоследовательностейможетбыть сформулирована следующим образом. Пусть задан источник дискретных сообщений основного ξ и вторичного η каналов связи, полностью определяемый алфавитом A = { a 1 ,..., a k } заданного объема K ; распределением априорных вероятностей

P (§ ) , P( n ) , заданных на последовательностях § ( a_v ..., a n ) ,п ( a 1 ,•••, a m ) ( a, e A ) произволь-ной длины n для основного и m – для вторичного источников сообщений ( n >>  m ). Пусть также источники дискретных сообщений допускают частичную потерю информации. Так как алфавиты источников дискретных последовательностей одинаковы и источники сообщений допускают потерю информации, рассмотрим композицию последовательностей §( a 1 ,..., a n ) , П( a 1 ,•••, a m ) с образованием групповой последовательности ^( a 1 ,..., a n ) длины m в виде

S (a l ,•••, a n ) = ^ (a l ,•••, a n ) ^{o П} (a l ,•••, a m ) , ⁽¹⁾ (где o знак композиции), которая заключается в замене части символов последовательности § ( a 1 ,..., a n ) на символы последовательности П ⁽ a 1 ,•••, a m ) по некоторому (неизвестному) правилу.

Необходимо определить правило, обеспечивающее минимизацию метрики Хэмминга D _Σ (определяемое количеством несовпадающих позиций между кодовыми последовательностями основного и преобразованного каналов)

D _s = D [4 i , Z i ] . (2) где § i , ^ i - соответственно i -ые символы кодовой последовательности основного канала и новой (преобразованной) последовательности при условии выделения последовательности П( a 1 ,•••, a m ) вторичного канала на приемной стороне.

Решение задачи вторичного уплотнения дискретных последовательностей на основе бинарного функционального преобразования (БФП)

Для определенности положим, что в качестве последовательностей основного ξ и вторичного η источников будем рассматривать сообщения с алфавитом A={0,1} с равновероятной выдачей нуля и единицы. Сообщения с подобными свойствами часто встречаются на практике. Разобьем исходные последовательности на подпоследова- тельности одинаковой длины – кодовые группы. Далее потребуем также, чтобы функциональное преобразование кодовых групп вторичного канала, обеспечивающее минимизацию функционала (2), удовлетворяло следующим свойствам:

• -    применение преобразования к кодовой группе с расстоянием до кодовых групп основного канала больше порогового должно приводить к уменьшению кодового расстояния;

• -    функция должна иметь обратную функцию, то есть если известно, что к данной кодовой группе была применена данная функция, то применение обратной функции обеспечивает восстановление исходного значения кодовой группы.

Таким требованиям может удовлетворять бинарная функция инвертирования

,    к. D[5„n] < l/2; (3) 1 In,. D[Si.n,] > l/2;

где ξ _i – i -ая кодовая группа последовательности основного канала; n i — i-ая кодовая группа последовательности вторичного канала; η _i – инвертированная i -ая кодовая группа последовательности вторичного канала; Z i — i-ая кодовая группа преобразованной последовательности. При этом длина всех групп выбирается одинаковой и равной величине l .

Покажем, что бинарная функция инвертирва-ония (3) обеспечивает уменьшение кодового расстояния между кодовыми группами до величины, меньшей или равной l /2. Вначале допустим, что кодовое расстояние между группами ξ _i и η _i меньше или равно l /2, то есть D [^ i , n i ] ^ n /2 . Это означает, что в группах различаются биты в половине позиций или менее. Следовательно, в рассмотренном случае инвертировать группу η _i не нужно, что соответствует верхней строке выражения (3).

Возможен обратный вариант, когда кодовое расстояние между группам ξ _i и η _i больше l /2. Это значит, что в группах имеется различие в более чем в половине позиций. Нетрудно видеть, что инвертирование η _i приведет к тому, что в тех позициях, где позиции различались, они будут совпадать. Так как таких позиций больше половины (> l/2),), следовательно, результирующее кодовое расстояние будет меньше l /2. Этот случай отражен во второй строке выражения (3).

Следовательно, вышеприведенная функция (3) обеспечивает уменьшение кодового расстояния между кодовыми группами до величины, меньшей или равной l /2 , что и требовалось показать.

Оценим «выигрыш» кодового расстояния (2) при использовании функции (3) с помощью иллюстративного примера. В качестве исходных данных рассмотрим все возможные кодовые комбинации наименьшей длины l = 3, которые приведены в верхней строке и крайнем левом столбце таблицы 1. В остальных ячейках таблицы 1 приведено кодовое расстояние между соответствующими группами. Жирным шрифтом выделены кодовые расстояния больше l /2.

Таблица 1. Кодовое расстояние между исходными кодовыми группами ξ _i и η _i

	000	001	010	011	100	101	по	111
ООО	0	1	1		1	2		3
001	1	0	2	1	2	1	3	2
010	1		0	1	2	3	1	2
011	2	1	1	0	3	2	2	1
100	1		2	3	0	1	1
101	2	1	3	2	1	0	2	1
по	2	3	1	2	1		0	1
111	3	2	2	1	2	1	1	0

В таблице 2 приведены кодовые расстояния между кодовыми группами последовательностей ξ _i и η _i полученной после инверсии η _i , для соответствующих пар групп, расстояние между которыми изначально было больше l /2 (для сравнения см. также таблицу 2).

Таблица 2. Кодовое расстояние между группами ξ _i и инвертированной группой η _i

	000	001	010	011	100	101	по	111
000	-	-	-	1	-	1	1	0
001	-	-	1	-	1	-	0	1
010		1	-		1	0		1
011	1	-	-	-	0	1	1	-
100	-	1	1	0	-	-	-	1
101	1	-	0	1	-	-	1	-
по	1	0	-	1	-	1	-	-
111	0	1	1	-	1	-	-	-

Сравнивая между собой содержание таблиц 1 и 2, можно заметить, что для отдельных кодовых групп инвертирование уменьшило расстояния с 2 до 1 и с 3 до 0. Если вероятности появления кодовых пар групп в исходных последовательностях ^(-) и п (•) одинаковы, то среднее кодовое расстояние между этими последовательностями уменьшается в 2 раза. Из приведенного примера видно, что применение преобразования (3) позволяет уменьшить кодовое расстояние между последовательностями основного и вторичного каналов. Однако если учесть необходимость хранения признаков использования преобразования (3), то проиллюстрированный выше «выигрыш» (определяемый критерием (2)) уменьшится.

Алгоритм образования вторичного канала в цифровой системе на основе БФП состоит из следующих шагов:

Шаг 1. Последовательности основного ^(-) и вторичного П (•) каналов разбиваются на группы ξ _i и η _i одинаковой длины l (l ≥ 3).

Шаг 2. Из всего множества разбиений последовательностей ^(-) и п ( " ) выбираются такие разбиения и сочетания групп ξ _i и η _i , в которых имеет место равновероятное распределение нулей и единиц.

Шаг 3. Для каждого сочетания групп ξ _i и η _i применяется формула (3). При этом во вновь образованную группу ζ _i добавляется признак инвертирования (или отсутствия инвертирования).

Шаг 4. Группы ζ _i объединяются в последовательность Z (•) • Далее вычисляется кодовое расстояние Хэмминга для каждого из разбиений последовательностей ^(-) и п(") •

Шаг 5. Выбираются такие разбиения последовательностей ξ _i и η _i , которые обеспечивают минимум функционала (2).

Последний шаг алгоритма обусловлен необхо-димостьюуменьшениястепениискаженийкодовой последовательности основного канала, вызванной необходимостью хранения признаков инвертирования (или отсутствия инвертирования).

Пример

Рассмотрим работу алгоритма с помощью примера. Исходные кодовые последовательности основного канала длины n = 2 и вторичного каналов длины m = 12, заданные случайным образом, приведены соответственно в первой и третьей строках таблице 3 (нумерация строк в таблице принята последовательной).

В примере последовательности ^(-) и п (•) разбиты на группы по l = 3 бита. В строках 3; 8 и 12 клетки таблицы разбиты на две части – в левой части приведен номер группы, а в правой – сама кодовая группа. В предпоследнем столбце курсивом выделены изменения в служебных битах. При этом для сравнения приведены три метода: первый метод не использует БФП (данные вторичного канал напрямую замещают данные основной последовательности), второй метод – с применением БФП, третий – модифицированный метод БФП с перестановкой групп последовательностей.

Как видно из таблицы 3, для первого метода изменяется только «информационная» часть основной последовательности, тогда как ее «служебная» часть остается без изменения. Кодовое расстояние Хэмминга в результате замещения D _∑ = 6.

В алгоритме БФП без перестановок изменяются «информационная» и «служебная» части последовательности. Изменения в служебных битах сообщения несут информацию для последующего выделения вторичных кодовых последовательностей и при этом показывают: 1 – инвертирование кодовой группы,0 – отсутствие инвертирования соответствующей кодовой группы «информационной» части этой последовательности.В этом случае суммарное кодовое расстояние (Хэмминга) равно D _∑ = 4.

Для случая применения метода БФП с перестановками помимо указания об использовании функционального преобразования (3) в служебной части сообщения необходимо указывать номер перестановки групп вторичных данных. В таблице 3 последние пять бит служебной последовательности (см. ту часть, которая выделена курсивом) определяют номер перестановки. Так как для 4 позиций примера возможны 24 перестановки, следовательно, наименьшее целое число бит, позволяющее их закодировать, равно 5. Биты, которые различаются в последовательности основного канала ^(-) и композиционной последовательности Z (•) , выделены подчеркиванием. Сравнивая строки 10 и 14 таблицы 3, можно видеть, что результирующее кодовое расстояние зависит от выбора порядка следования групп последовательности п (•) , и при соответствующем выборе такого порядка можно достичь минимума кодового расстояния Хэмминга, равное в нашем случае D _∑ = 3. В таблице 3 подчеркиванием указываются несовпадающие позиции последовательностей ^(-) .

Наиболее «трудоемким» моментом в приведенном алгоритме является формирование таких правил обхода последовательности, которые позволят проверить все возможные варианты сочетаний групп ^(-) и п (•) • В самом простом варианте данную задачу можно решить путем полного перебора всех сочетаний, что для длинных последовательностей займет очень много машинного времени и приведет к существенному запаздыванию передачи сообщений. Поэтому здесь еще одной важной подзадачей является разработка упрощенных правил обхода (анализа) последовательностей. Другим очевидным вариантом преодоления данной трудности является разбиение последовательностей ^(-) и п (•) на фрагменты небольшой длины и работа с ними.

Таблица 3. Иллюстрация к примеру

ξ	000		001		010		011		100101110 111
Без применения бинарного функционального преобразования
η	№0	110	№1	100	№2	010	№3	000	Служебн. посл.
ζ БЕЗ БФП	11 0		1 0 0		010		0 00		100101110 111
D[ ξ , ζ БЕЗ БФП ]	2		2		0		2		0	D ∑ = 6
С применением бинарного функционального преобразования
Без перестановки групп последовательности η
η	№0	110	№1	100	№2	010	№3	000	Служебн. посл.
ζ БФП	00 1		0 1 1		010		1 11		1 1 0101110 111
D[ ξ , ζ БФП ]	1		1		0		1		1	D ∑ = 4
С перестановкой групп последовательности η
η	№3	000	№0	110	№2	010	№1	100	Служебн. посл.
ζ БФП И ПЕРЕСТ.	000		001		010		011		01 010 0 110 111
D[ ξ , ζ БФП И ПЕРЕСТ. ]	0		0		0		0		3	D ∑ = 3

Если принять следующие рекомендации:

• -    последовательности ξ и η делятся на фрагменты длиною, равной целому числу групп;

• -    группы должны начинаться с позиций, кратных длине группы;

число вариантов сочетаний уменьшается и их можно задать простым перечислением.

Для определения числа возможных вариантов перестановок можно воспользоваться формулой P _m =m! ( m – число групп). Для вышеприведенного примера P ₃ = 3! = 6. С увеличением числа групп количество перестановок резко возрастает, поэтому максимально возможное число групп во фрагменте последовательностей на практике может быть ограничено величиной, скажем равной 10.

В случае, когда требуется большее быстродействие и последовательность ^0 значительно (в разы) превышает по длине последовательность П (•), предлагается модифицированный алгоритм БФП. Последовательность ^0 в этом случае разбивается на участки, каждый из которых в несколько раз длиннее группы ηi . Далее перебором находится номер позиции на участке, начиная с которого будет размещаться преобразованная группа ηi . Этот алгоритм работает быстрее предыдущего, но для размещения одного и того же количества групп ηi требует в несколько раз большей длины последовательности ^0.

Для работы с потоковыми данными более удобным представляется отказ от перебора всех вариантов и работа с группами в порядке поступления последовательностей. В модельных экспериментах в качестве последовательности ^(•) использовались наименее значащие разряды изображения формата bMP, а в качестве последовательности п (") текстовые сообщения.

Заключение

Для оценки эффективности метода БФП с точки зрения повышения информационного содержания в композиционной последовательности и увеличения соотношения сигнал/шум (задаваемой метрикой (2)) проводился ряд модельных экспериментов. Программа исследования заключалась в следующем: датчиком псевдослучайных чисел генерировались бинарные последовательности основного ^0 и вторичного каналов П (") длиной соответственно 1 000000 и 1 00000 байт, характеризуемый равномерным законом распределения символов. Затем различными модификациями метода БФП осуществлялась композиция этих последовательностей (1) так, чтобы минимизировать метрику (2). Здесь следует сделать небольшой комментарий. Так как обе дискретные последовательности ^(-) и п(') имеют равномерный закон распределения символов, вообще говоря, они характеризуются минимальной информационной избыточностью, что делает проблематичным использование методов вторичного уплотнения. Однако это «компенсируется» тем увеличением длины композиционного Z (") файла (количества разрядов) по сравнению с ^(-) из-за необходимости включения служебной информации – признака инвертирования (функции инвертирования) замещаемой вторичной последовательности. Тем самым увеличивается информационная избыточность композиционного файла Z (•) ■ Количественным показателем оценки изменения степени избыточности композиционного файла служило увеличение его размера (длины). Поэтому для оценки эффективности применения методов БФП использовалось отношение изменений кодового расстояния Хэмминга и длины композиционной последовательности. Результаты эксперимента приведены на рис .1. Из рис. 1 видно, что чем большей информационной избыточностью характеризуется последовательность основного канала, тем меньше степень его искажения при применении метода БФП (при условии неизменной длины вторичной последовательности) в процессе уплотнения.

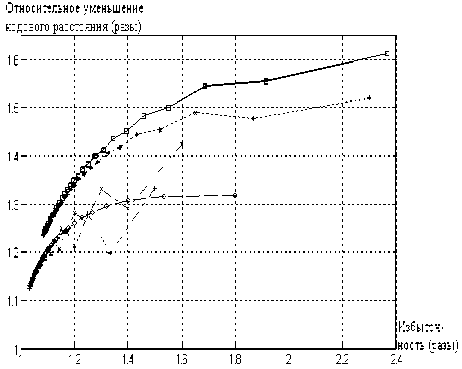
Рис.1. График оценки эффективности БФП