Вторичное уплотнение нестационарных сигналов критериальными методами

Одним из направлений увеличения информационной емкости ТС являются методы вторичного уплотнения сигналов, предложенные в работе [1], позволяющие передавать короткие сообщения небольшого содержания (например, команд управления, идентификации, аутентификации и т.д.) без организации дополнительных физических каналов связи.

Основная идея методов заключается в инкапсуляции (смешивании) эргодических, неортогональных в гильбертовом пространстве сигналов основного и вторичного каналов с пересекающимися спектрально-временными характеристиками на бесконечном интервале наблюдения, что накладывает существенные ограничения на свойства уплотняемых сигналов. Также предложенные методы не учитывают ряд особенностей, а именно:

• -    в системах связи имеет место нестационар-ность уплотняемых сигналов;

• -    нестационарность трактов передачи;

• -    критичность к задержкам в процессе передачи сообщений;

• -    переход к цифровым системам связи.

Следовательно, актуальным остается вопрос совершенствования методов вторичного уплотнения с учетом вышеперечисленных факторов. В основе дальнейших исследований предлагается использовать методику разложения сигналов в нестационарный ряд Солодовникова-Семенова (представляющий подкласс обобщенного ряда Фурье) [2], который позволяет преодолеть вышеуказанные ограничения.

Вторичное уплотнение сигналов может быть рассмотрено на основе концепции «синтез-анализ», включающей следующие подзадачи:

• -    синтез желаемых спектральных характеристик сигнала вторичного канала;

• -    анализ (выделение) сигнала вторичного канала.

Решение подзадач удобно осуществлять критериальными методами, позволяющими получить формализованные решения.

Постановка задачи

Математическая модель нестационарного вторичного уплотнения сигналов представлена на рис. 1.

x g (^T)

X(Tк A z^(T )

k i (9,т )

x ( 9 )

~ ( 9 )        j

* e (6 )

* e 2 ( 9 )

Х д ( 9 )

Рис.1. Математическая модель нестационарного вторичного уплотнения

На рис. 1 х ( т ) - нестационарный сигнал основного канала, для которого существует и известна его нестационарная спектральная характеристика (НСХ) X ( i , t ), ( i = 0; 1; 2...) ; x _g ^{( т} ) – нестационарный сигнал дополнительного канала связи, для которого также существует НСХ X _д ( i , t ), ( i = 0; 1; 2 ...), подлежащая определению; ~( У ) - сигнал оценки основного канала.

Составляющие НСХ X ( i , t ), X д ( i , t ) представляют собой коэффициенты разложения сигналов х ( т ) , x g ^{( т} ) в обобщенный ряд Фурье по нестационарному ортонормированному базису у ( i , t , т ) , определенному на нестационарном отрезке [ t - T ( t ), t ] и содержащему в общем случае комплексные функции. НСХ X ( i , t ) , X д ( i , t ) сигналов х ( т ) , Х д ( т ) определяются по формуле:

t

X ( i , t ) = j ^ * ( i , t , т ) x ( т ) d т ,       (1)

t - T ( t )

где у * (i, t ,т) - комплексно-сопряженный нестационарный ортонормированный базис, определенный на нестационарном отрезке [t - T(t), t] [2]. Переход от нестационарной спектральной характеристики к функции времени осуществляется по формуле обратного перехода

X ( т ) = ^ X ( i , t ) v ( i , t , T ). (2)

i

Сумма сигналов z ( t ) = х ( т ) + х д ( т ) поступает на вход взвешивающего фильтра с известной импульсной передаточной функцией к 1 ( 0 , т ) . Взвешивающий фильтр должен быть физически реализуем и асимптотически устойчив. С физической точки зрения взвешивающий фильтр является фильтром предыскажения.

Вторичный сигнал x д ( т ) вносит искажения в исходный сигнал х ( т ) , то есть выступает в качестве помехи. Задача формирования вторичного ка-наласостоитвопределениижелаемойНСХсигна-ла вторичного канала X д ( i , t ), ( i = 0; 1; 2 ...), при которой обеспечивалось бы его ограниченное влияние на основной. С математической точки зрения необходимо обеспечить выполнение функционального равенства вида:

t

J ( t ) = J e ² ( t ) d T = c ( t ) ,          (3)

t - T ( t )

где e 1 ( t ) = ~ ( t ) - x ( t ) - сигнал на выходе первого элемента сравнения (ошибка воспроизведения сигнала основного канала), c ( t ) - функция времени, ограниченная сверху некоторым значением inf( с ( t )) <  с .

С другой стороны, х ( т ) также искажает сигнал вторичного канала связи х д ( т ) . Для того чтобы обеспечить уверенное выделение сигнала вторичного канала связи из суммы z ( t ) на приемной стороне, необходимо обеспечить минимум функционала вид

t

J 2 ( t ) = J е^т ) dT , где e ₂ ( т ) = ~ ( т ) - хд ( т )

t - T ( t )

– сигнал на выходе второго элемента сравнения.

Для решения подзадачи синтеза сигнала нестационарного вторичного канала необходимо найти минимум следующего функционала:

J (t,a) = J 1 (t) + a (t) J 2 (t) = n                                               (4)

= £ (E1 (i, t) E *1 (i, t) + a (t) E2 (i, t) E *2 (i, t)) i=0

где E 1 (i, t ) - НСХ ошибки в основном канале, E ₂ ^{( i} , t ) - НСХ ошибки во вторичном канале, E *1 (i, t ) , E *2 ( i , t ) - комплексно-сопряженные НСХ основного и вторичного каналов, a ( t ) -множитель Лагранжа.

С точки зрения концепции «синтез-анализ» важным этапом является выделение сигнала вторичного канала в условиях относительно малого соотношения сигнал/шум. Рассмотрим постановку подзадачи синтеза фильтра выделения сигнала вторичного канала.

Вторая подзадача по существу является модификацией традиционной задачи оптимальной фильтрации.

На вход одноканальной ТС, структурная схема которой представлена на рис. 2, имеющей нулевые начальные условия, поступают в момент т = 0 полезный сигнал х д ( т ) (сигнал вторичного канала) и аддитивная помеха х ( т ) (сигнал основного канала). Полезный сигнал и помеха являются случайными, в общем случае нестационарными функциями времени с известными нестационарными спектральными плотностями S' X d X d ( h i , t , t ) , S 'XX ( h , i , t , t ) , определяемыми по формуле [2]:

S' xx ( h , i , t , t ) = X ( h , t ) X ( i , t ) , (5)

где X ( h , t ) - НСХ центрированного сигнала центрированного случайного сигнала ^х сл ^{( т} ) = ^{х ( т} ) - x ^{( т} ) .

Синтезируемый фильтр выделения должен наилучшим образом преобразовывать полезный сигнал и подавлять помеху. Идеальное преобразование полезного сигнала задается двумерной нестационарнойпередаточнойфункцией(ДНПФ) W z ( h , i , t , t ) . За критерий оптимальности системы примем условие минимума среднеквадратической ошибки г _ск ( 0 ) = ~ _д ( 0 ) - х д ( 0 ) в каждый момент времени t : s ск ( 0 ) = min при 0 <  0 <  t .

Требуется найти оптимальную ДНПФ W ( h , i , t , t ) , обеспечивающую минимум среднеквадратической ошибки 8 ск ( 0 ) в каждый момент времени t .

к ( 9 , т )

^х д ^{( т} )

z (^T )

"ШПУ ^k 2 (п,^т )

Х д ( 9 )

—qp>^k ск ( в ) Х д (9т

Рис. 2. Модель нестационарного вторичного канала

На рис. 2 к1 (0,т) - импульсная передаточная функция взвешивающего фильтра, k2 (0,т) - импульсная передаточная функция фильтра выделения сигнала вторичного канала, хд (0) - сигнал оценки вторичного канала, 8ск (0) - ошибка оценивания сигнала вторичного канала. Суммарная импульсная передаточная функция тракта неста- ционарного вторичного канала определяется следующим выражением:

t

k (0 ,т ) = jk 2 (0 ,n)kx (п ,т W].      (6)

t - t ( t )

После перевода уравнения (6) в спектральную область, оно примет вид

W ( h , i, t, t ) = Е W 2 ( h , v , t , tW ( v , i, t , t ) , (7)

ν где W1 (v, i, t, t) - ДНПФ взвешивающего фильтра, W2 (h,v, t, t) - ДНПФ фильтра выделения сигнала вторичного канала, W(h, i, t, t) - ДНПФ вторичного канала.

Из двух множителей правой части уравнения (7) неизвестной является ДНПФ фильтра выделения вторичного канала W 2 ( h , v , t , t ) , в то время как ДНПФ взвешивающего фильтра W 1 ( v , i , t , t ) известна. Таким образом, после нахождения ДНПФ ТС W ( h , i , t , t ) , необходимо определить ДНПФ W 2 ( h , v , t , t ) фильтра выделения нестационарного вторичного канала, используя формулу (7).

Решение подзадачи синтеза сигнала вторичного канала

Учитывая структурную схему системы (см. рис. 1), определим выражение для сигнала ошибки на выходе первого элемента сравнения:

61(0)=~0) - X6) = Е{№) + Xg(i,t))H(i,t,0) — X0, i где H(i,t,0) - нестационарная сопряженная передаточная функция. Умножим левую и правую части данного уравнения на ^(h,t,0), проинтегрируем по dθ и просуммируем по h . В итоге получим:

t

Е j e , ( 9 >* ( h , t, 9 )d 9 = Е E , (h, t) = ^h t - T ( t )                                    ^h

t

= ЕЕ{(X(i, t) + Xд (i, t)) jH(i, t, 9>* (h, t, 9)d9} - h i                                       t-T (t)

• - Е ^x( 9> * (h, t, 9 )d 9 =

h t - T ( t )

= ЕЕ{( X (i, t) + Xд (i, t))W (h, i, t, t)} - Е X (h t) hi                         h где

W(h, i, t, t) = jdO jv* (h, t, O)v(i, t, т)k(O, т)dT -t-T (t) t-T (t)

– двумерная нестационарная передаточная функция (ДНПФ) взвешивающего фильтра; E 1 (h, t ) -НСХ сигнала на выходе первого элемента сравнения, ( h = 0... n ) .

Выражение для НСХ сигнала на выходе второго элемента сравнения определяется аналогично. Таким образом, функционал (4) будет выглядеть следующим образом:

J ( t ) = J , ( t ) + a ( t ) J 2 ( t ) =

= Е[Е{(Х (i, t) + Xд (i, t))W(h, i’t, t)} - X (h, t))]x hi x [Е{(Х * (i, t) + X *g (i, t))W * (h, i, t, t)} - X * (h, t)] +

+ a(t)Е[Е{(X (i, t) + Xд (i, t))W (h, i, t, t)} - -Xd (h, t)] x hi x [Е{(X * (i, t) + X *Д (i, t))W * (h, i, t, t)} - X * д (h, t)], где X (i, t), Xд (i, t) - сопряженные НСХ сигналов основного и дополнительного каналов.

Необходимым условием минимума функционала является равенство нулю его первой производной [3]. Вычислим частную производную dJ ( t )/ X g ( v , t ) , где v = (0 ... n) принимает все значения дискретной переменной ортонормиро-ванной системы функций, относительно которой определена НСХ сигнала вторичного канала, и приравняем ее к нулю (для упрощения записи опустим индексы времени t ):

-dJ— = (1 + a )[ Е Е (X ( i ) + X Д ( i )) W ( h , i ) - dX g ( v )              h i

• - Е ( X ( h ) + a X g ( h ))]W * ( h , v ) - h

• - a Е (X ( h ) + X _g (h)) W( v , h) - aX _g ( v ) = 0.

h

Перенесем в правую часть слагаемые, имеющие в качестве множителя НСХ сигнала основного канала:

(1+а)ЕЕХд (i)W(h,i)W*(h,v)-аЕХд (h)W*(h,v) - hi                   h

- а Е Х д ( h ) W ( v , h) - aX g ( v ) =

h

= -(1+а)ЕЕх(i)W(h,i)W* (h,v)+ hi

+ЕХ(h)W* (h, v)+аЕх(h) W(v, h), hh где (v = 0... n),(h = 0... n),(i = 0... n) . В итоге получим n уравнений относительно всех элементов матрицы НСХ сигнала вторичного канала.

Для решения данной системы уравнений воспользуемся методом Крамера. Для этого представим систему уравнений в виде произведения матриц: AX _д = B . Диагональные элементы матрицы A определяются выражением:

A ( v , h) = (1 + a ) Z W ( i , hW ( i , v)] - a ( W * (h, v) + W ( v , h) - 1), i

(v=h), остальные элементы – выражением

A(v, h) = (1 + a) Z Wi, h) W ( i , v)] - a(W (h, v) + W ( v , h)),

i

(v = 0...n),(h = 0...n),(i = 0...n).

Элементы матрицы B определяются как

B(v) = -(1 + a )£ £ X (i)W (h, i)W * (h, v)] + hi

+ £ X ( h )[ W * ( h , v) + a W (v, h)],

h

(v = 0 ... n),(h = 0 ... n ),( i = 0 ... n ).

Формальное решение системы уравнений относительно искомых элементов матрицы НСХ сигнала вторичного канала по формуле Крамера имеет вид

X д ( i , t , a ) = ^A-,               (8)

A где A = det A - определитель матрицы A, A i — алгебраическое дополнение, получаемое путем за-меныi-гостолбцав А столбцом [B(0)...B(n)]T, α – множитель Лагранжа.

После определения НСХ сигнала вторичного канала необходимо вычислить значение множителя Лагранжа, который, в общем случае, является функцией времени. Для этого необходимо подставить найденное значение НСХ X _д(i,t, a ),(i = 0 ... n ) сигнала вторичного канала в уравнение (4) и решить его относительно неизвестного множителя Лагранжа a ( t ) .

Решение подзадачи выделения сигнала вторичного канала

Составим выражение для среднеквадратической ошибки системы, имея ввиду, что £ с_ск ( 0 ) = £ W 2 ( 0 ) + £ N ( 0 ) , где £ W и £ N ⁽⁰ ) - средние значения квадратов ошибки в преобразовании полезного сигнала и ошибки, обусловленной прохождением помехи через систему, соответственно. Согласно структуре ТС, представленной на рис. 2, нестационарные спектральные плотности составляющих среднеквадратической ошибки можно представить в виде (матричном):

SV (t, t) = W£ (t, t)S'xdxd (t, t)W; (t, t) ,

S' N (t, t ) = W ( t , t )S' XX (t, t ) W * (t, t ) ,

S E (t, t) = S XdXd (t, t) + S XX (t, t) ,

где ДНПФ, обуславливающая ошибку в преобразовании сигнала, определяется выражением W _£ ( t , t ) = W z ( t , t ) - W ( t , t ) ; S 'W ( t , t ) , S N ( t , t ) , S e ( t , t) – спектральные плотности сигналов £ W , £ NN и £ с_кк ( 0 ) , соответственно. Учитывая, что £ 2 (6 ) = P ( t , 6)S' _E (t, t ) P ( t ,6 ) (обратное преобразование от спектральной плотности сигнала) [2], окончательно выразим среднеквадратическую ошибку через искомую ДНПФ

£ Ск ( 0 ) = P ( t , 0 )[{ W z (t, t ) -

• -    W(t, t )}S' x d x d (t, t){W z (t , t ) - W(t, t )} * +

+ W(t , t)S' XX (t, t)W * (t , t )] P * (t, 0 ), где P (t, 0 ) - ортонормированные нестационарные базисные функции.

Устойчивость синтезируемого фильтра обеспечивается путем умножения его ДНПФ на матрицу физической реализуемости

W (h, i, t , t ) = ZZ J (h, ^ , v , i, t, t )WW( ^ , v , t , t ) ,

μν где W(hi, i, t, t) - ДНПФ физически реализуемого звена, W(ц,v, t, t) - ДНПФ в общем случае физически нереализуемого звена, J(h, ц,v, i, t, t) -матрица физической реализуемости ДНПФ [2].

Наложим на искомую ДНПФ условие физической реализуемости и определим частную производную от £ с2К_к ( 0 ) по матрице W ( t , t ) . Возвращаясь к символу W ( t , t ) , получим:

dl^ = P(t,0)P * (t,0 ) x dW(t,t)

x[- Z U (t)VV(t)S X _d X _d (t,t){W z (t^ - W(t,t)} * +

+ Z U 1 (t)V l (t)S' XX (t,t)W (t,t)]=0. l

Интегрируя правую и левую части последнего выражения по 0 на интервале [t - T(t), t] и, учитывая, что j P(t, 0) P* (t,0 ^d^t = E, t-T (t)

будем иметь:

• -    S x d X d ( t , t ) W z ( t , t ) - W ( t , t )} * + S XX ( t , t ) W * ( t , ^) = 0.

Далее, найдя сопряженную матрицу от левой части и учитывая, что матрицы спектральных плотностей S' X d X d (t, t ) , S' XX ( t , t ) эрмитовы, необходимое условие минимума среднеквадратической ошибки приведем к виду:

W ( t , t )[ S ' X d X d ( t , t ) + S ' XX ( t , t )] = W z ( t , t ) S ' X d X d ( t , t ).

Так как идеальным преобразованием является воспроизведение, W z ( t , t ) = E , окончательно получим:

W(t,t) = S' X d X d (t,t)[S X d X d (t,t) +S' XX (t,t)] - 1 (9)

Из уравнения (9) видно, что искомая ДНПФ полностью определяется матрицами спектральных плотностей S' X d X d (t, t ) , S' XX ( t , t ) сигналов основного и дополнительного каналов. При этом, как было указано выше, после определения оптимальной ДНПФ W ( t , t ) ТС, необходимо подставить найденное значение W ( t , t ) в формулу (7) с целью определения ДНПФ W 2 ( t , t ) фильтра выделения сигнала вторичного канала.

Решение задачи синтеза характеристики фильтра выделения производилось, исходя из условия, что значения спектральных плотностей сигналов основного и вторичного каналов известны на приемной стороне, что в реальных условиях недостижимо. Однако значения характеристик сигналов основного и вторичного каналов с некоторой погрешностью могут быть получены на приемной стороне из сигнала оценки основного канала путем применения к нему алгоритма нестационарного вторичного уплотнения. Такой подход к устранениюаприорнойнеопределеннос-ти позволяет избежать передачи информации о характеристиках сигналов системы нестационарного вторичного уплотнения, что положительно сказывается на общей пропускной способности ТС. Решение задачи устранения априорной неопределенности при приеме сигналов нестационарного вторичного канала в рамках данной статьи не рассматривается.

Пример

Пусть сигнал основного канала (меандр) определен на интервале две секунды и описывается выражением:

х ( т ) = sign (sin(2n"T)), т = [0,2] , где sign - знаковая функция. Фильтр предыскажения представляет собой апериодическое звено первого порядка, ДНПФ которого описывается выражением

W (h, i,2,2)

Wuht (h, i,2,2) 0,003 + Wuht (h i,2,2) , где WUHT (h, i,2,2) - ДНПФ интегрирующего звена на интервале две секунды [2]. Множитель Лагранжа задан и равняется a(t) = а = 5. Необходимо найти значение НСХ сигнала вторичного канала Xд (i,2) и ДНПФ фильтра выделения W2 (h, i,2,2) сигнала вторичного канала, а также определить оценки сигналов основного хф) и вторичного ~Д (6) каналов.

Вычисления будем производить в численном виде (в символьном виде конечные выражения слишком громоздки) в нестационарном гармоническом базисе [2], определяемом по формуле:

^(i, t , т ) = V2/ 1 cos( inT 1 1 ) .

Определим ДНПФ фильтра предыскажения (в примере ограничимся первыми тремя членами i = 0;1;2 ):

" 0,9970 W i (h, i,2,2) = -0,0001 _v -0,0063

0,0001 -0,0063"

0,9999   0,0110

-0,0110 0,9866

Далее по формулам (1) и (8) определим НСХ сигналов основного и вторичного каналов, соответственно:

X ( i , 2) = ( 0,0283 0,5273 0,0400 ) , X д ( i ,2) = ( 0,0020 -0,0026 0,0394 ) .

Затем найдем НСХ оценки сигнала основного канала ~ (0 ) , как реакцию фильтра предыскажения на входное воздействие z ( т ) :

XX(i,2) = (0,0298 0,5255 0,0362), и ДНПФ фильтра выделения сигнала вторичного канала:

⎜⎛ 0,0027

W ₂ (h,i,2,2)=⎜ - 0,0080 ^⎜⎝ 0,0569

- 0,0026 0,0476 ⎟⎞

0,0077 - 0,1408 ⎟

- 0,0551 1,0021 ⎟⎠

Из сравнения X ( i ,2) , X ( i ,2) видно, что искажения сигнала основного канала небольшие.

Далее найдем НСХ оценки сигнала дополнительного канала х д (0 ) как реакцию фильтра выделения на входное воздействие ~ (0) :

ХХ д ( i ,2) = ( 0,0022 -0,0065 0,0459 ) .

Из сравнения X д ( i ,2) , X _д ( i ,2) видно,что характер НСХ оценки сигнала и сигнала вторичного канала в целом совпадают,что говорит о возможности выделения сигнала вторичного канала на приемной стороне.

Заключение

Для более полного исследования предлагаемых методов было произведено численное (компьютерное) моделирование представленного примера при увеличенномдо21числебазисныхфункцийразложе-ния и множителе Лагранжа равном a ( t ) = а = 1,5.

Результаты численного моделирования представлены на рис. 3-6. Из рис. 5-6 видно, что при небольшом уровне искажения сигнала основного канала обеспечивается выделение сигнала вторичного канала с помощью оптимальной фильтрации. При этом о наличии или отсутствии сигнала вторичного канала в оценке сигнала основного канала на определенном интервале можно однозначно судить по амплитуде оценки сигнала вторичного канала.

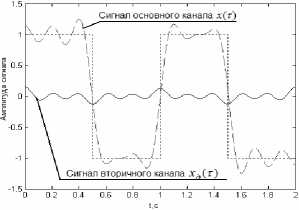
Рис. 3. Сигналы основного и вторичного каналов

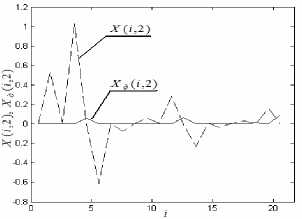
Рис. 4. НСХ сигналов основного и дополнительного каналов

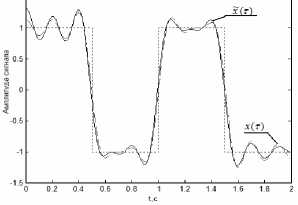
Рис. 5. Оценка сигнала ~ ( т ) и сигнал х( т ) основного

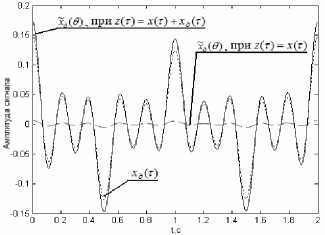
Рис. 6. Оценки сигнала вторичного канала ~ _д (0 ) и сигнал х д ( т ) вторичного канала

Для оценки пропускной способности вторичного канала было проведено численное моделирование нестационарного вторичного уплотнения звукового сигнала формата W AV и цветоразностных сигналов цветного изображения без сжатия и со сжатием по стандарту MPEG-2.

Для звукового сигнала была получена скорость вторичного канала, равная 1630 бит/с. При этом искажения звукового сигнала не отмечались, вероятность ошибочного приема сигнала вторичного канала приближалась к нулю.

Для цветоразностных сигналов цветного изображения без сжатия и со сжатием по стандарту MPEG-2 скорость вторичного канала составила 1890000 и 66448 бит/с, соответственно. Вероятность ошибочного приема сигнала вторичного канала также близка к нулю. Уровень искажения изображения приемлемый. При этом временная задержка сократилась в 3240 и 31500 раз для сигналов изображения со сжатием и без сжатия, соответственно, по отношению к ранее предложенным методам вторичного уплотнения [1].