Вторичное уплотнение узкополосных сигналов в радиоканалах с неограниченной памятью
Автор: Костюк Денис Сергеевич, Кузнецов Игорь Васильевич, Султанов Альберт Ханович
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Технологии телекоммуникаций
Статья в выпуске: 4 т.9, 2011 года.
Бесплатный доступ
В статье рассмотрена задача вторичного уплотнения телекоммуникационных каналов с учетом модуляционных преобразований сигналов. Представлена модель вторичного уплотнения каналов, получены общие соотношения для нахождения характеристик вторичного канала и фильтра выделения сигналов.
Вторичный канал, фильтр выделения, спм, узкополосный сигнал, модель вторичного уплотнения, радиоканал
Короткий адрес: https://sciup.org/140191507
IDR: 140191507 | УДК: 621.396
Текст научной статьи Вторичное уплотнение узкополосных сигналов в радиоканалах с неограниченной памятью
Современные тенденции развития телекоммуникационных систем связаны с повы- шением их пропускной способности, приданием им свойств большей эффективности и экономичности. Одним из альтернативных способов повышения пропускной способности телекоммуникационных систем является вторичное использование каналов, позволяющее организовать передачу дополнительной информации без расширения используемой полосы частот. Идея данных методов не нова и широко используется в системах телевизионного вещания для передачи звуковой и сервисной информации. Недостатком подобных систем является их узкая направленность на реализацию в конкретном стандарте вещания. Более эффективными методами повышения пропускнойспособности современныхсистем связи являются методы вторичного уплотнения [1]. Основная идея методов заключается в наложении друг на друга эргодических, неортогональных в гильбертовом пространстве сигналов основного и вторичного каналов с пересекающимися частотно-временными характеристиками, при условии ограничения их взаимного шумового влияния.
Стоит отметить, что ранее не рассматривалась задача вторичного уплотнения каналов с учетом модуляционных преобразований сигналов. Следовательно, актуальной является задача разработки методов вторичного уплотнения и выделения (синтез фильтра выделения вторичного сигнала) каналов с учетом модуляционных преобразований сигналов. Решаемую задачу можно отнести к задаче условной оптимизации Винера-Хопфа.
Постановка задачи
На рис. 1 представлена модель вторичного уплотнения телекоммуникационных сигналов в радиосистемах. Пусть на вход узкополосного модулятора (с несущей частотой ®н ) подается первичный случайный центрированный сигнал x ( t ) с известной функцией спектральной плотности мощности (СПМ) Флт(>) . На выходе модулятора осуществляется смешение модулированного сигнала Х„(0 и сигнала вторичного канала y ( t ). Групповой сигнал
z(O = ^m(O + XO, (1)
подается в канал связи. В приемной части при помощи передаточной функции фильтра выделения ^U™) осуществляется выделение сигналов основного и вторичного каналов.
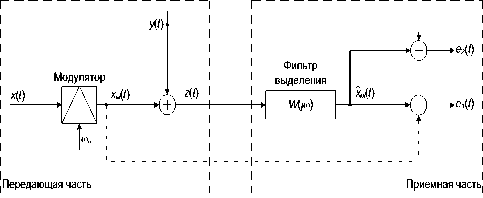
Рис. 1. Модель вторичного уплотнения
В связи с тем, что спектральные характеристики сигналов xм ( t ) и y ( t ) пересекаются, сигналы основного и вторичного каналов оказывают взаимное искажающее действие друг на друга. Другими словами, вторичный сигнал y ( t ) выступает по отношению к xм ( t ) в качестве помехи. Задача формирования вторичного канала связи состоит в определении желаемой СПМ ФугОю) сигнала y ( t ), при которой обеспечивалось бы его ограниченное воздействие на основной и вторичный сигнал оставался бы малозаметным на фоне основного. С математической точки зрения необходимо обеспечить выполнение функционального равенства вида:
У. =--- limM^ —------!----- >dito=c‘, (2)
1 2п/_^^ [ Т J где E\jto^X = И>Ж UmVHN]" ^, и®\ Б}Ы – спектральная характеристика ошибки рассогласования e1(t) между сигналами на выходе первого виртуального элемента сравнения (см. рис. 1); с – известная величина, имеющая размерность единиц мощности, определяющая степень скрытости вторичного сигнала; j = 4^\ -мнимая единица; х(М – изображение по Фурье оценки сигнала основного канала на выходе фильтра выделения; Xм(jω) – изображение по Фурье модулированного сигнала основного канала; Y(jω) – изображение по Фурье сигнала вторичного канала; T – время наблюдения. С другой стороны, xм(t) также искажает сигнал вторичного канала связи y(t). Для того чтобы обеспечить уверенное выделение сигнала вторичного канала связи, из суммы z(t) на приемной стороне необходимо обеспечить минимум функционала вида: т 1 ' f г алГ^(7®)’^(-7®)1 ■ , .х J2= hmM^ ‘ —- ^to^min, (4) ~ 2kj J т^ L J где Е, (у бу) = X (j®) - У (» = (5) = ^(убу)[Хм (убу)+ У(Убу)]- У(Убу), где E2tN – спектральная характеристика ошибки рассогласования e2(t) между сигналами на выходе второго виртуального элемента сравнения (см. рис. 1). Таким образом, математическую задачу синтеза вторичного радиоканала связи сформулируем следующим образом: найти функцию СПМ сигнала вторичного канала и передаточную функцию фильтра выделения с учетом известной функции СПМ сигнал основного канала и ограничений (2) и (4). Решение В качестве исходных данных для синтеза вторичного канала выступает спектральная плотность мощности немодулированного сигнала основного канала. В дальнейшем для удобства все расчеты будут производиться для модулированного сигнала с учетом «переноса спектра», поэтому увяжем СПМ немодулированного и модулированного сигналов. Согласно [2] спектральная плотность узкополосного модулированного сигнала xм(t) может быть определена следующим образом: Sm IN = °’5^ Uto"" 7®н ) + °,5Sx (-/co- j®H); (6) где 0,5 SN->B) – спектральная плотность амплитуд узкополосного аналитического сигнала -YM(6; 0,55, (-/co-/coh) – спектральная плотность амплитуд узкополосного комплексно-сопряженного аналитического сигнала Хм№; ®H – несущая частота сигнала. Определим спектральную плотность мощности основного модулированного сигнала с учетом переноса спектра на несущую частоту ®H в канале с неограниченной памятью, для этого воспользуемся соотношением [3]: м XX ^7 ) (7) где T – время наблюдения. Подставим выражение (6) в выражение (7) и, с учетом свойств аналитического сигнала [2], получим 1 . p Фм w(j®)=^фп (У®-У®,,)+-Ф1т(-y®-y®„), (8) где Фл-а(>-М)– функция СПМ узкополосного аналитического сигнала xм(t), равная Ф at (yco - y®H) где Oxx(-jto-jN - СПМ узкополосного комплексно-сопряженного сигнала xм(t): Флт(-У®-У®н) = lim^ M S.x- (-у® - У®н) • к (У®+У®„) . С учетом узкополосности сигнала два слагаемых в формуле (8) не «перекрываются» по спектру. Исходя из вышеизложенного, рассматриваемую задачу можно представить как линейную, пользуясь при этом низкочастотными эквивалентами моделей канала и сигналов основного и вторичного каналов. Для удобства вычислений введем обозначения: у® - У®н; -у® - у®н. Дальнейший синтез искомых параметров вторичного канала будем производить относительно переменной У® . Решение задачи проводится на основе метода проектирования оптимальных линейных систем и заключается в отыскании минимума функционала вида: J = Jx*aJ.=— Ф7(У®*)^®*, (9) 1kJ где а – неизвестный множитель Лагранжа, подлежащий определению; ФДУ®) – некоторая подынтегральная функция скалярного функционала. Отметим, что в силу четности дробно-рациональных функций СПМ сигналов их можно представить в виде произведения двух функций (факторов) [1]: ф (у®’) = ф" ,-(ую‘)ф- Д-jVy, ф)г(7ю*) = ф((уоУ)ф;(-у™*), где Фу (У®*) – известная функция, нули и полюсы которой лежат в левой части комплексной полуплоскости; Фу(-У®‘)- известная функция, нули и полюсы которой лежат в правой части комплексной полуплоскости. Рассмотрим подынтегральное выражение (9): ф J Uro*) = l,im ^ м(е, (УбУ* )ЕХ (-jto*) + + а[^2(Убу‘)^2(-У»*)])- = lim mJ 5x (y® - yroH) • 5л- (-(У® - У®„)) I, Г^ос у | I Подставим в формулу (10) выражения (3) и (5) для ExkNy ^2(7®*) и комплексно сопря- дФJ №YH®‘) = ФмЛ-(Х )X X [(a +1>(-j® ) W(y co*) - a ^(у оз* )-W(-у оз*) ]+ + [(1 + а)/С(уоз* ^(-уоз*) -afWf-yto*)+^(уоз*) - l)]x хФХуоз*)-^(-ую*); м АЙ-(Х) + Фм хН®*Жи®) + дФ, апч-уи) = W(J®> +фм л О’ Ж W®)+Ф}7 О*))] - [Фм XX U® ) + Фм X 0®" Ж (-J® ) + + Ж v Н®’ Ж О*) + ф п- О* ))]= ^2 (-7ю*), где Жю‘) и ^("У®’) – неизвестные функции, полюсы которых находятся в правой полуплоскости комплексной плоскости. Приведенные ниже выражения (11)-(12) можно рассматривать как модификацию известного [3-4] уравнения Винера-Хопфа в комплексной области. В итоге получим систему из уравнений: ФмЖЮ)Х х[(а+#(-уоз*)^(ую*)- (Н) 4(1+а)170ю*)1Ж7ю*)-^^ хФ^ЖЖСО*); ^(y"to*)x х[(а+1)(фм лх.О'ю*)+Фм xW® ЖО*)+ +Ф) v(>* )Ф~(^ (12) -[ф« ла(Ую*)+Фм ЖЮ*Ж(-7Ю*) + +аЖ а-(-7ю* )фу(7ю*)+фуу(7ю*))]=^2 (-7ю* )• Покажем, что (11)-(12) в общем случае имеют ненулевое решение, то есть Ф;(7ю*) * О и ^(уго* ) ^ 0. Сначала докажем факторизуемость коэффициентов, заключенных в квадратные скобки при Ф;.(уоз*) и ^(ую*) уравнений (11) и (12) соответственно. Утверждение 1. Если ^(у'со) дробно-рациональная функция, то функция вида F(yco) =FF(y®) + ^(-усо) является четной. Доказательство. Так как ^(ую)- дробно-рациональная функция, то ее можно представить в виде ^(7Ю) = aUtoMbU«>V где многочлены a(jto) и й(ую) представлены в виде равенств: a(jto) = ^ a^jtoY и й(уоз) = ^ 6/усо)', /=0 ./=0 где а; и bj — некоторые действительные числа. Согласно условию утверждения имеем, что . «(уоз) а(-уоз) F( /го) = ——+--= ьи®) b(-ja) (13) = ay®)bHtoFra(^^ b^jto^b^-jto) Из (13) видно, что четность знаменателя F(jto) не вызывает сомнения. Докажем четность числителя F( j®) ■ Подставим в числитель (13) вместо a(yco), a(-yco) и b(j®), b(-j®) соответствующие выражения многочленов и раскроем скобки. В результате получим aU®)b(-jto) + a(-jtoMM = = ^((-l)'a,Z3/yto)'+/ +(-l)/a,Z,/yto)'+^ (14) где I = 0,77 и у = 0,777 . Из (14) видно, что если один из индексов i или j четный (нулевой индекс будем считать четным), а другой нечетный, то выражение под знаком суммы равно нулю. Действительно, пусть 7 = 2k - четный, y = 2/ + l- нечетный (k и l – некоторые целые числа), тогда т/^Дусо)^' - ajbjUtoY^' = 0, при этом показатель степени при переменной 7 to – нечетный: z + j — ^k + /) + 1 • Следовательно, слагаемые числителя (14) с нечетными степенями при переменной У CD равны нулю. Аналогично можно показать, если оба индекса i и j нечетные (или четные), то в этом случае слагаемые при y'to будут иметь четные степени. На самом деле, если i = 2k +1 и y = 2/ + l – нечетные, то - aibj(jtoy+J - а-.Ь^]^^1 - где в общем случае -2aibi(jtoY+i + 0 и при этом сумма z + у — 2 ^k + / + 1) принадлежит множеству четных чисел. Таким образом, из четности числителя и знаменателя F(yco) следует, что эта функция является четной. Так как слагаемые коэффициента при ФуО®*) представляют собой четные функции, к выражению [(1+аУо* WH® ) - а(^Н® ) + Mj® ) -1)] можно применить операцию факторизации. Докажем существование ненулевого решения уравнения (11) методом от противного, то есть допустим, что ф^(Х)=о, ф:и»о и для простоты положим а = 1. Из условия а = 1 легко следует факторизуемость коэффициента при Ф^О®)-Тогда уравнение (11) можно представить в виде: [2Ж(/со^У<о*)-(1^ [2^0* Wjto vVu^WH®))]” ’ где обозначения [ Л(» ]+ и [ AQto) ] указывают на то, что нули и полюсы выражений под этими знаками лежат соответственно в левой и правой частях комплексной полуплоскости. Левая часть этого уравнения имеет все полюсы в левой полуплоскости, а правая часть уравнения – все полюсы в правой полуплоскости. Поэтому функция комплексного переменного (15) должна быть аналитической во всей плоскости. Из свойства аналитичности функции комплексного переменного уравнения (13) (согласно теореме Лиувилля [4]) получим, что Ww-Mj^w^ (16) ^мИУ® )=°- Так как выражения 2^(уФ*Ж(-уФ*) и wo*wh^ отличаются друг от друга многочленами в их числителях, следовательно, в общем случае можно утверждать, что IW^tE W<-j№ ) * WQV) + W(-jro ) откуда следует Vwuto^-jtoMWU»Vw<-j^x ^»xU®V^ и далее согласно условию Kx^n 0 следует, что в (16) имеется противоречие, что и доказывает существование ненулевого решения (11). Существование ненулевого решения уравнения (12) доказывается аналогичным методом. После проведения соответствующих операций факторизации и сепарации искомые решения (11) и (12) определяются следующими выражениями: Фу(У®) = +аИу<0* )F(-JCO*) -a^(->*)+W^j® ) -1| Ф+^(Уо>*)((а+#О^^^^^ (M Фм Х)У®,+<11ч A (^Фм.а^^лЪю^/ю)^^®^^^^ где обозначение [^(7®)]+ указывает на то, что полюсы выражения, заключенного под этим знаком, лежат в левой полуплоскости комплексной плоскости. Выражения (17) и (18) являются формальным (общим) решением системы уравнений (11)-(12). Выражение (17) является фактором СПМ, поэтому для нахождения СПМ вторичного сигнала (на положительных частотах) необходимо воспользоваться соотношением [3]: Ф}у(7Ф* ) = Фу О* )Фу (-jto ), где Ф; (-усо*) = Фу (-у<в*). Найденная функция Фу (уф*) сигнала вторичного канала связи и передаточная функция взвешивающего фильтра ^(уф*) зависят от множителя Лагранжа а, который можно определить в результате подстановки (17)-(18) в выражение (2) и решения полученного равенства. Утверждение 2. Система уравнений (11) и (12) имеет ненулевое решение: ф+(уф*) У О и ^(уФ*)#0. Доказательство. Вернемся к функционалу (2): 1 vr Г Ex(jtoyEx(-jcoy\ 1 J, = limM^———-—1—-—->dKO = cx 2тд_™” I т J С математической точки зрения выбор параметра c произволен, поэтому а = /(с2), откуда следует, что выбор а также произволен. Примем а = 1 и покажем, что система имеет ненулевое решение. Подставим в (12) значение a= 1: ВДх х[2(фм лхОф*)+ф; х-Х)фЖ)+ +ф: х^ w-nwyyU® ))]- (19) -кxx-Uto )+ф„хо*)ф;(-Х)+ + (Фм X Н® Ж U® ) + Ф>тО®* ))] Ж (“У® )" Так как слагаемые (или их сумма) коэффициента при ^(уф*) представляют собой четные функции, то к выражению 2(Ф м XX U® ) + Ф м X W® )Ф У U®‘ ) + Ф М х U® )Ф у (-У®*) + Ф it U® )) можно применить операцию факторизации. Тогда (19) может быть представлено в виде: вторичного сигналов на приемной стороне линейная зависимость не является оптимальной. Пример Рассмотрим случай a ^ 1. Передаточную функцию фильтра будем искать в виде дробно-рациональной функции. Сигнал основного канала физически реализуемый процесс. Так как в общем случае мы имеем систему из двух уравнений с четырьмя неизвестными, то непосредственно из уравнений (11)-(12) определить Ф№*) и WU®)в общем случае не представляется возможным, поэтому будем искать частные решения этой системы. Пусть ф:.у0ф*)=1, передаточную функцию резонансного фильтра выделения будем искать в виде «низкочастотного» эквивалента: 2Щ>*)х wu®) = а + jto* ФмЛаЖ Н^ х^® Ш® )+< x^W-j®WY^ Фм ХХ^®^^ X^toWtito^+^M ^-jtSWjtih+^Y^i6^ Для определения фу (У®* ) воспользуемся выражением (17), в которое подставим (23). Задача определения же®*) и ф;о’) сводится к нахождению параметра a. После подстановки для фу (уф* ) получим Фм X^J®)+Фм X )+фм А^ЭД^ФФу}^'0^ Оба члена левой части данного уравнения имеют все полюсы в левой полуплоскости, а правая часть уравнения – все полюсы в правой полуплоскости. Поэтому функция комплексного переменного (20) должна быть аналитической во всей плоскости. Из свойства аналитичности функции комплексного переменного (согласно теореме Лиувилля [4]) получим, что 2ИУ/оГ)х Фм^“ )+al« ^"J®Wi®)+ай xU®W-j^+tI,y^Jto) Фм x)ptoV^ xti® WA/to )+^ xH® ^'б^+Фу^'б?) Отсюда следует, что Для нахождения Фу ( jo) ) подставим (21) и a = 1 в (17): ф;о*) = 2[ф: д-О*)^ =2Ф: хи® ). (22) Из (22) следует, что зависимость между вторичным и основным сигналами линейна. Заметим, что с точки зрения разделения основного и Подставим (24) в уравнение (12) и решим его. В итоге получим для параметра a: Чтобы получить выражения для 1Г(Х) и фу ОФ*), необходимо подставить найденный параметр а в (23) и (24). Полученная функция фу (уф* ) сигнала вторичного канала связи и передаточная функция фильтра выделения ^(уф*) зависят от множителя Лагранжа a, который можно определить в результате подстановки этих соотношений в (2) и решения полученного равенства. В ходе дальнейших исследований системы уравнений (11)-(12) было установлено, что порядок знаменателя передаточной функции фильтра выделения должен быть минимум на единицу больше порядка знаменателя ф: л(уф*)- Так, на- + . * x- пример, если м Л a A- jto то передаточную функцию фильтра выделения необходимо D WUtoV • искать в виде (b+jto*Xc+/co*) На основе полученных данных было проведе- но моделирование синтезированной системы в математическом пакете MATLAB. В ходе модели- рования сравнивались синтезированная система и система вторичного уплотнения, в которой параметры приемного тракта (фильтра выделения) не синтезировались: было показано, что в синтезированной системе передачи отношение сигнал/ шум больше на 7,38 дБ, что свидетельствует о повышении качества передачи; кроме того, исходя из значения дисперсии второго разностного сигнала (это значение меньше как минимум в 10 раз), можно заключить, что при приеме возможно обеспечение более уверенного выделения сигнала вторичного каналов, чем в системе, в которой параметры приемного тракта (фильтра выделения) не учитываются.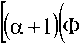
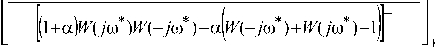

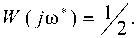
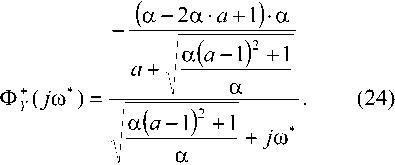
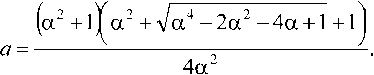
Список литературы Вторичное уплотнение узкополосных сигналов в радиоканалах с неограниченной памятью
- Султанов А.Х., Кузнецов И.В., Блохин В.В. Сигнальные и структурные методы повышения информационной емкости телекоммуникационных систем. М.: Радио и связь, 2006. -325 с.
- Зюко А.Г., Кловский Д.Д. Теория электрической связи: учебник для вузов. Радио и связь, 1998. -432 с.
- Цейтлин Я.М. Проектирование оптимальных линейных систем. Л.: Машиностроение, 1973. -240 с.
- Свешников А.Г., Тихонов А.Н. Теория функций комплексной переменной. М.: Наука-Физ-матлит, 1999. -315 с.
- Свешников А.А. Прикладные методы случайных функций. М.: Наука, 1968. -464 с.
- Тихонов В.И. Статистическая радиотехника. М.: Радио и связь, 1982. -624 с.


