Второе решение уравнений Максвелла

Автор: Хмельник С. И.

Журнал: Доклады независимых авторов @dna-izdatelstwo

Статья в выпуске: 35, 2016 года.

Бесплатный доступ

Предлагается новое решение уравнений Максвелла для вакуума. Предварительно отмечается, что доказательство единственности известного решения основано на законе сохранения энергии, который не соблюдается (для мгновенных значений) в известном решении. Предлагаемое решение не нарушает закон сохранения энергии. Кроме того, в этом решении электрическая и магнитная компоненты напряженностей в электромагнитной волне сдвинуты по фазе. Приводится подробное доказательство для заинтересованного читателя.

Короткий адрес: https://sciup.org/148311754

IDR: 148311754

Текст научной статьи Второе решение уравнений Максвелла

В последнее время критика справедливости уравнений Максвелла слышится со всех сторон. Уверенность критиков создается, прежде всего, нарушением закона сохранения энергии. И, действительно, "плотность потока электромагнитной энергии (модуль вектора Умова-Пойнтинга) «пульсирует» по гармоническому закону. Не нарушается ли здесь закон сохранения энергии?" [1]. Безусловно, нарушается, если электромагнитная волна удовлетворяет известному решению уравнений Максвелла. Но ведь другого решения нет: "Доказательство единственности решения в общих чертах сводится к следующему. Если имеется два различных решения, то их разность вследствие линейности системы тоже является решением, но при нулевых зарядах и токах и нулевых начальных и граничных условиях. Отсюда, пользуясь выражением для энергии электромагнитного поля и законом сохранения энергии заключаем, что разность решений тождественно равна нулю, т. е. решения одинаковы. Тем самым единственность решения уравнений Максвелла доказана" [2]. Таким образом, единственность решения доказывается на основе применения того закона, который нарушается в этом решении.

Другим результатом, следующим из существующего решения, является синфазность электрической и магнитной компонент напряженностей в электромагнитной волне. Это противоречит представлению о беспрерывном преобразовании электрической и магнитной компонент энергии в электромагнитной волне. В [1], например, этот факт относится к "порокам современной классической электродинамики".

Такие результаты, следующие из известного решения уравнений Максвелла, позволяют усомниться в достоверности уравнений Максвелла. Подчеркнем, однако, что эти результаты следуют только из найденного решения. Но это решение, как указано выше, может быть иным.

Ниже выводится другое решение уравнений Максвелла, в котором плотность потока электромагнитной энергии остается постоянной во времени, а электрическая и магнитная компоненты напряженностей в электромагнитной волне сдвинуты по фазе.

Вначале рассмотрим решение уравнений Максвелла для вакуума. Эти уравнения в системе СГС имеют вид [3]:

1 д H „ rot ( E ) +---= 0 ,

c д t

/ х 1 дE rot (H )—— = 0, c д t div (E )= 0, div (H )= 0.

В системе цилиндрических координат r, ф, z эти уравнения имеют вид:

E r д E r 1 ^дЕ ф д E z 111

r д r r дф д z

L5Ez E=Mr, r дф дz

дEr дE ——--z- = M дz д r ф, (3) E дE 1 QE _+ + ф -1 .^E. = Mz, r дr r дф (4) Hr+dH_+1.^+dHz = 0, r д r r дф дz (5) 1 дH дНф =j J.. r дф дz (6) дHr —^Hz = J дz д r ф, (7) Нф 8Нф 1 дHr + * =J, r дr r дф (8) 1 дE J = , c д t (9) 1 дH M =. c д t (10) Для сокращения записи в дальнейшем будем применять следующие обозначения: co = ео8(аф + xz + ®t), (11) si = 5,т(аф + xz + tot), (12) где а, X, to — некоторые константы. Представим неизвестные функции в следующем виде:

Jr • = Jr (r 'c^O , (13) Jф• = jф(.r) si, (14) Jz • = jz (r) si , (15) Hr • = hr (r )co , (16) Hф• = hф( r) si, (17) Hz • = hz (r) si , (18) Er • = er (r )si , (19) Еф. = еф( r) co, (20) Ez • = ez (r) co , (21) Mr • = mr (r ^co, (21) Мф^ = тф( r) si, (22) Mz • = mz (r)si , (23) где j(r), h(r), e(r), m(r) - некоторые функции координаты r .

Непосредственной подстановкой можно убедиться, что функции (13-23) преобразуют систему уравнений (1-10) с тремя аргументами r, ф, z в систему уравнений с одним аргументом r и неизвестными функциями j(r), h(r), e(r), m(r).

В приложении 1 показано, что у такой системы существует решение, имеющее следующий вид (в приложении 1 см. (24, 27, 18,

31, 33, 34, 32) соответственно):

X = ~ c

e ( r) , ,< x ^e Ф ^(r ) л

-r ^ + e r ( r ) - ^ф—a = 0 , rr

^ф + e ф ( r ) ^r ^{( -} a - 0, г г	(25)
Ут- ' + h r ( r ) + ^h ^ < r ’ a - 0 , rr	(26)
h ^ t r l + _й ф ( r ) + **_ ' • „ - 0, rr	(27)
^h ф ( ^r ) ^- ^e r ⁽ ^r J,	(28)
h r ⁽ ^r ^)- - ^e ф ( ^r ),	(29)

Тем самым мы получили монохроматическое решение системы уравнений (1-10). Переход к полихроматическому решению может быть выполнен с помощью преобразования Фурье. Очевидно, если решение существует в цилиндрической системе координат, то оно существует и в любой иной системе координат.

Таким образом, мы получили общее решение уравнений Максвелла в вакууме.

3. Напряженности

Система уравнений (2.24-2.29) определена – имеется 6 уравнений для 4-х функций e_r , e _ф , h r , h _ф и двух скаляров a , to . Рассматривая эту систему, можно заметить, что она эквивалентна двум уравнениям (2.24, 2.25) для функций e_r , e _ф . Две другие функции h_r , h _ф определяются по (28, 29) и удовлетворяют уравнениям (26, 27).

Два дифференциальных уравнения (2.24,	2.25) могут	быть
решены при данных начальных условиях Предварительно рассмотрим уравнение вида	и данном	α .
ay + у ' = 0 , x Решения этого уравнения имеют вид:		(1)
У = X ^— a ,		(2)
у = 0 .		(2а)
Уравнения (2.24, 2.25) могут быть заменены уравнениями вида
e r + e , h*^ ’ ( 1 — а ) = 0, Г		(3)
( e r — e , ’А ’ ( 1 + а ) = 0 . Г В соответствии с (1, 2) находим для (3):		(4)
⁽ ^e r ⁺ e , ) = ^Ar “ - ¹ .		(5)
⁽ ^e r ⁺ e , ) = ⁰ • В соответствии с (1, 2) находим для (4):		(5а)
⁽ ^e r ^— e , ) = ^Ar ^— ^а - ¹ .		(6)
⁽ e r ^— e , ) = ⁰ .		(6а)

Здесь ( А\2 ) - амплитуда напряженности . Таким образом, допустимы несколько решений уравнений (3, 4). В дальнейшем мы рассмотрим решение (5, 6а). Из (5) и (6а) следует:

e r = e , = 0.5 A • r ^a ^- ¹ . (7)

При этом er2 + e, )= A • r2(a-1). (10)

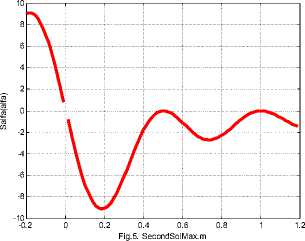
На рис. 1 показаны, например, графики функций (7, 10) при A = — 1, а = 0.8 .

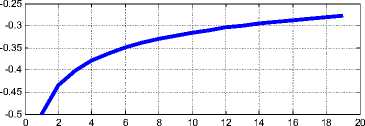
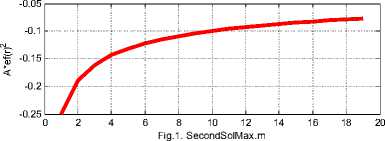
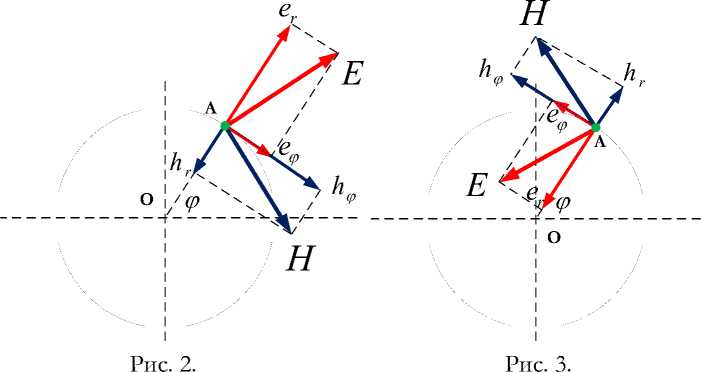
На рис. 2 показаны векторы напряженностей, исходящие из точки A ( r, ф ) . Напомним, что проекции А _ф ( r ) = e r ( r ) и h_r ( r ) = - е _ф (r ) - см. (2.28, 2.29). Направления векторов e r ( r ) и е _ф (r ) выбраны так: e_r ( r ) > 0 , е _ф (r ) < 0 . При этом векторы E, Н всегда ортогональны . Сумма модулей этих векторов определяется из (2.17, 2.18, 2.20, 2.21, 2.28, 2.29) и равна

W = E ² + Н ² = ( e_r ( r >i "2 + ( ф г s ) + ⁽ h ( r co ) + ( ф г co )

или

W = ⁽ ^e _r ⁽ ^r )) ^{+ (} е ф ⁽ г ) ) (18)

- см. также (10) и рис. 1. Таким образом, плотность энергии электромагнитной волны постоянна на всех точках окружности данного радиуса .

Решение существует и при измененных знаках функций (2.11, 2.21). Этому случаю соответствует рис. 3. Рис. 2 и рис. 3 иллюстрируют то, что возможны два вида циркулярной поляризации электромагнитной волны .

На рис. 4 для демонстрации сдвига фаз между компонентами волны (2.13-2.23) показаны функции

co = еоз(аф + xz + ®t), si = sin( аф + xz + ®t)

или эквивалентные им при z = ct функции

I 2 a )

. . ( 2a)

si = sin l аф + z

I c

co = cos l аф + — z I ,

I c )

При ф = 0, 2 ю / c = 0.1 эти функции принимают вид co = cos ( z ) , si = sin ( z ) и показаны на рис. 4.

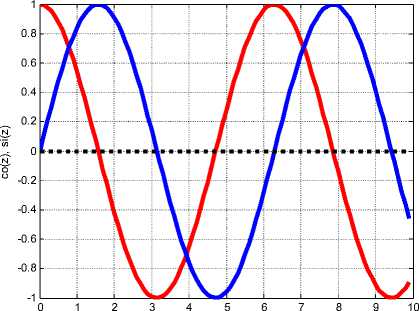
Fig.4. SecondSolMax.m

3. Потоки энергии

Плотность потока электромагнитной энергии – вектор Пойнтинга

S = nE х H, (1)

где

П = с / 4 п . (2)

В цилиндрических координатах r , ϕ , z плотность потока электромагнитной энергии имеет три компоненты S_r , S _ϕ , S_z ,

■ S Z 1

■

si ² "

S =

S ^ф

= n Л

⁵ Ф

• si • co

dr • dф

l S z Z

r , ϕ

_ s z

si • co

направленные вдоль радиуса, по окружности, вдоль оси

соответственно.	Они определяются по формуле
	■ S r "		■ Б ф Ы₂ - к₂Н ф -
^S =	^S Ф	= n ⁽ E ^х ^Н ) = n	E_zH r - E r H_z	. (4)
	_ S z _		^EH — ^Е ф ^Н г

Из (2.12-2.17, 3.4) следует, что поток, проходящий через данное сечение волны в данный момент времени, где sr = (e9hz - e-h-)

s 2 = ( ^e z h r - ^e r h z У (6)

s z ^{= (} еЛ - e ^ h r )

В приложении 1 показано, что h_z ( r ) = 0 , e_z ( r ) = 0 .

Следовательно, sr = 0, s^ = 0 , т.е. поток энергии распространяется только вдоль оси oz и равен

S = S z = n JJ [ s z • si • co ^r • dф . (7)

r , ϕ

Отсутствие потока энергии по радиусу означает, что область существования волны НЕ расширяется. Подтверждением этому является существование лазера.

Найдем s_z . Из (2.28, 2.29) получаем:

еЛФ = e2 , e^hr =- e2.

Из (7, 8, 9) получаем:

sz =e2+e2 )

Таким образом,

S = n JJ [e2 + e2 )• si • co ]^r • d2.(11)

r , ϕ

Отсюда, как показано в приложении 2, следует, что

S = ⁽ ^cos ⁽ ⁴ ^an ) 1 )[ ⁽⁽ e 2 + e 2 )/ r ). 16 απ r	(12)
Из (10, 3.12) находим:
S = cA ( 1 - cos ( 4 an ))[ ( r ²⁽ ^a ^-1) )/ r . 16 απ r	(12а)
Пусть R – радиус кругового фронта волны . Тогда
2 ( a-DV. ^R^ S int r ^J( dr ( 2 a - 1 ) ,	(13)
^S alfa = - ⁽ ¹ ^- c^os ⁽ ⁴ ^an ⁾⁾ , α	(14)
cA
S =--- S^S rnf ₁₆ π alfa int	(15)

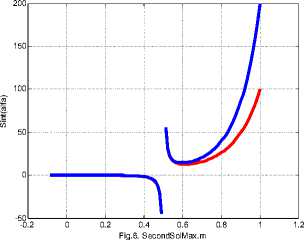
На рис. 5 показана функция Salfa (α) (13), а на рис. 6 показана функция Sint (α) . На рис. 6 верхняя и нижняя кривые относятся соответственно к R = 200 и R = 100. Из формулы (15), рис. 5 и рис 6 видно, что поток энергии является положительным, например, при A = -1, а = 0.8.

Поскольку поток энергии и энергия связаны соотношением

S = W • c , то из (15) можно найти энергию единицы длины волны:

W = ---- SalfaS_m f

₁₆ alfa int

В приложении 2 показано также, энергии на окружности данного радиуса вида

S rz = ( e r ² + е² _ф )fe in ( 2 a^ + 4 oz/ c ) .

Отсюда и из (3.10) следует:

S rz = A • r ²⁽ ^a ^- ¹ ⁾ sin ( 2a^ + 4^z/c ) .

что плотность потока определяется функцией

На рис. 7 показаны эти функции при A = 1, а = 0.8, r = 1 и двух значениях второго слагаемого: 0, 0.5 – см. сплошную и пунктирную линии соответственно.

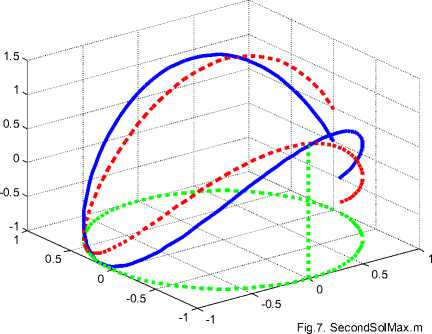
Отсюда следует, что

• плотность потока неравномерно распределена по сечению потока – существует картина распределения плотности потока по сечению волны;
• эта картина вращается при перемещении по оси oz;
• поток энергии (15), проходящий через площадь сечения, не зависит от t, ф, z; главное, что эта величина не изменяется во времени, и это соответствует закону сохранения энергии.

Полученное решение описывает волну. Его основные отличия от известного решения состоят в следующем:

1. Мгновенный (а не средний по некоторому периоду) поток энергии не изменяется во времени, что соответствует закону сохранения энергии .
2. Поток энергии имеет положительное значение.
3. Поток энергии распространяется вдоль волны
4. Магнитная и электрическая напряженности на некоторой оси координат r , ф , z сдвинуты по фазе на четверть
5. Решение для магнитных и электрических напряженностей является вещественным .
6. Решение существует при постоянной скорости распространения волны.
7. Область существования волны не расширяется, что подтверждается существованием лазера.
8. Векторы электрической и магнитной напряженностей ортогональны .
9. Возможны два вида циркулярной поляризации электромагнитной волны
10. Волна и ее энергия определены, если заданы параметры

периода .

A , о , R , а . При данных R , 5 может быть найден параметр α .

Приложение 1.

Рассматривается решение уравнений (2.1-2.10) в виде функций (2.13-2.23). Далее производные по r будем обозначать штрихами. Перепишем уравнения (2.1-2.10) с учетом (2.11, 2.12) в виде

^r ⁽⁾ + e’ ( г ) ^ф а %• e_z ( г ) = 0 , г г	(1)
- ¹ ■ e z ⁽ г⁾ ^а + q г ) х = m_r ⁽ ^r ) , r	(2)
e r ⁽ ^r ) х ^- ^e Z ⁽ ^r ) = m q ^{( r} X	(3)
^eq^(r V. ₍x e_r (r ) ⁺ e q ⁽ ^r) ■ ^а = m z ⁽ ^r X rr	(4)
^r ⁽ ) + h' _r( r ) + ^q а + X" h_z ( r ) = 0 , rr	(5)
¹ ■ h z ⁽ ^r) ^a - h q ⁽ ^r ) X = j, ⁽ ^r ) r	(6)
- ^h r ⁽ ^r ) X ^- ^h Z ⁽ ^r ) = ^j q ⁽ ^r X	(7)
^{Ф +} ^h ^q ⁽ r ) ⁺ r ⁽ ) " ^{a j}z ⁽ r ) = ⁰ , rr	(8)
ω ωω Jr = ^—e r , j q = e q , j z = e z , c cc	(9)
ω ωω m r = -h r , m q =-- h q , m z =-- h z , c cc	(10)

Умножим (8) на ( — x") и учтем (9). Тогда получим:

^X " ^h q ⁽ ^r ) i \ X " h_r (r ) , X® < x (x X- h q ( r ) ^rV ■ a + ■ e z ( r ) = 0, r rc	(11)
или
^C ^X ^hqn + c ^X h q ( r ) + c ^X **-a - X - e z ( r ) = 0, ω r ω ω r	(12)
Сравнивая (1) и (12), замечаем, что они совпадают, если
c^h q ⁽ ^r ) = e r ⁽ ^r Z, ω	(13)
- ^C ^X h r ⁽ ^r ) = e q ⁽ ^r ) • ω	(14)
Важно отметить, что такое сравнение справедливо только e_z ( r ) ^ 0. При этом в соответствии с (9) и j_z ( r ) ^ 0 .	при
В уравнениях (13, 14) сделаем замену в соответствии с (9):
Xh q ⁽ ^r ) = ^- ^j _r ⁽ ^r Z,	(15)
^- X ^h r ⁽ ^r ) = ^j q ⁽ r ) •	(16)

Уравнения (15, 16) совпадают с (6, 7) при h z ( r ) = 0 . Отсюда следует

Лемма 1. При e z ( r ) Ф 0 система уравнений (1, 5-9) совместима только в том случае, когда h z ( r ) = 0 .

Рассмотрим теперь случай, когда e z ( r ) = 0 . При этом в соответствии с (9) получим j_z ( r ) = 0 . Тогда исходная система (1, 58) примет вид:

e (r) , г z X e;(r)

-r2^- + er (r) - —а = 0,(17)

rr hr^r) + hr(r)+ ^^а + X" hz(r) = 0,(18)

1 ■ hz (r )a - h;( r) X = j (r)

- hr(r )X - h(r) = j;(r X

h^r) + h; (r) + hr^) ■ a = 0,

Подставим (9) в (17). Тогда получим:

jr^ + jr (r) + j^r) a = 0,(22)

Подставим (19, 20) в (22). Тогда получим:

-4 ■ hz(r)a -1 ■ h;( r) x+1 ■ hz(r)a - h;(r) x+(- hr(r )x - hz(r))a=0 r rrr

или

■ hz(r)a -1 ■ h;(r) x - h;(r) x - hr(r) —=0

rrr

При этом для вычисления трех напряженностей получим три уравнения (19, 21, 23). Исключим h ; ( r ) из (21, 23):

1 , z x 1 z .( 1 , z x , /\a ) , Z x xa „

— ■ hz (r)a---h;(r)X +| - ■ h;(r) + hr (r )— IX - hr (r )^ = 0 r r V r r )

или — ■ h z ( r ) a = 0 или h z ( r ) = 0 . Таким образом, и при e z ( r ) = 0 r ²

должно соблюдаться условие h z ( r ) = 0 . Отсюда следует

Лемма 2. При e z ( r ) = 0 система уравнений (1, 5-9) совместима только в том случае, когда h_z ( r ) = 0 .

Из леммы 1 и леммы 2 следует

Лемма 3. Система уравнений (1, 5-9) совместима только при h z ( r ) = 0 и, в соответствии с (10), m_z ( r ) = 0 . Однако допустИм случай, когда e z ( r ) Ф 0 и j_z ( r ) Ф 0 .

Доклады независимых авторов	2016 выпуск 35
При e z ( r ) = 0 и h z ( r ) = 0 уравнения (1,	5-9) принимают
следующий вид - уравнения (1, 5, 8) упрощаются, заменяются уравнениями (13, 14):	а уравнения (6, 7)
e ( r ) , г( X ^еФ⁽r ) л -r ^ + e , ( r ) - —a = 0 , rr	(3.1)
h=X ' + K, ( r ) + h^ a = 0 , rr	(3.2)
^Х\ , ⁽ r ) = e r ⁽ r ^- ω	(3.3)
- ^C ^X h r ⁽ r ^- = Ф ^r ) , ω	(3.4)
+ _h ■ ( r ) + h r L' . a = 0 . _r ϕ _r	(3.5)
Аналогично доказывается

Лемма 4. Система уравнений (1-5, 10) совместима только при e z ( r ) = 0 и, в соответствии с (9), j z ( r ) = 0 . При этом аналогично формулам (24, 28) получаем формулы

e ( r ) , ,₍ X Ф r ) Л -r ^ + e , ( r ) - —a = 0 , rr	(4.1)
% ⁽ ^r ) X = - — h_r ⁽ ^r ^- c	(4.2)
^e r ⁽ ^r ^- X = ^— h p ⁽ ^r X c	(4.3)
^еФ^(r) , f _X e_r(r ) ^ф + e , ( r ) ^rv .-a = 0, rr	(4.4)
hXr^-^ «, ( r ) + ^А ф < Г 2 a = 0 . rr	(4.5)
Из леммы 3 и леммы 4 следует Лемма 5. Система уравнений (1-10)	совместима только	при
h z ⁽ ^r ) = ⁰ , ^e z ⁽ ^r ) = ⁰ , m_z ⁽ ^r ) = ⁰ , j z ⁽ ^r ) = ⁰ .
Следовательно, исходная система уравнений (1-10) принимает
вид уравнений, перечисленных в леммах 3 удобства читателя:	и 4. Объединим их	для
e_T ( r ) , , ₍ x ^e Ф ⁽ ^r ) Л -r ^ + e , ( r ) - ^Ф—a = 0 , rr		(24)
^e Ф ⁽ ^r ) X = ^- ^— h r ⁽ ^r ^, c		(25)

e r ⁽ ^r ) X = ^m h v ⁽ ^r X c	(26)
^еФ^(rX. - ( X e_r(r ) A + е ф ( r ) ^rV •• а = 0, rr	(27)
h^ ' + _A; ( r ) + h v < r > а = 0 , rr	(28)
^Х Ф ⁽ ^r ) X = ^m e r ⁽ ^r )1 c	(29)
^- h r ⁽ ^r ) X = ^m e v ⁽ ^r ), c	(30)
h v l r l + X ( r ) + h . l r .l a = 0 . _r ϕ _r	(31)

Умножим уравнения (26, 29). Тогда получим:

( m

- e r ( rX ⁽ ^r ) X = -I - I e r ( r X ⁽ ^r )

V c )

или x=m c.(32)

Подставляя (32) в (26, 29), получаем:

Хф (r) = er V )

Таким образом, при условии (32) уравнения (26, 29) эквивалентны одному уравнению (33). Аналогичное соотношение следует из (25, 30):

hr (r)=-фr)

Итак, система уравнений (24-31) эквивалентна системе уравнений (24, 27, 28, 31-34).

Приложение 2.

В (3.11) показано, что поток энергии, проходящий через сечение волны,

S = n jj [(er2 + e\ ) si •co dr • ф(1)

r ф

Пусть скорость распространения волны постоянна и равна с. Тогда z = Ct .(2)

Тогда из (2, 2.11, 2.12, 2.30) получаем:

co = cos(av + xz + mt) = cos(av + (2^ c )z )

и, аналогично,

si = sin (аф + (2m c )z )•(4)

Имея в виду (3, 4), перепишем (1) в виде:

⁵ = 1 n JJ ( 2 + e p )s in ⁽ ² ( ap + ( 2 ^ с ) z ) drdp . r , ϕ

Таким образом, плотность потока энергии на окружности данного радиуса определяется функцией вида

S rz = e 2 + e p )^in(2 ap + 4az) с ) . (5а)

При z=0 на оси oz имеем:

⁵ = 2 П JJ ( 2 ⁺ e p )^ ⁱⁿ ^ap^idp .

r , ϕ

Далее из (6) находим:

5 =

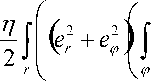
) ) sin ( 2ap ) dp dr

) )

Имеем:

2 π ₁

sin ( 2ap ^dl p = sin ( 2a.p ) dp = —(1 - cos ( 4 na )) .

2 α

ϕ 0

Из (7, 8) получаем:

5 = 4П (1 - cos(4an )]J ((e2 + ep )/r ).

Подставляя сюда (3.2), окончательно получаем:

⁵ = — ⁽ ¹ ^- co^s ⁽ ⁴ ^an ⁾⁾j ⁽⁽ ^e 2 + e p )/ r ).

16 απ

Очевидно, при любом выборе точки z=0 на оси oz последнее соотношение сохраняется.

Статья научная