Введение пространства L2,w при построении проекционной оценки плотности вероятности

Введение. Для решения задач классификации, распознавания, диагностики технических систем и др., возникающих в том числе в аэрокосмической отрасли, большое значение имеет качество восстановления неизвестной функции плотности вероятности непрерывных случайных величин. Зачастую закон распределения исследуемых случайных величин имеет сложную структуру: плотность вероятности разрывна, многоэкстремальна и т. д. В таких условиях часто применяются непараметрические методы оценивания функции плотности вероятности, основанные на оценках М. Розенблатта и Э. Парзена [1-3]. Также большое распространение получила проекционная оценка, предложенная Н. Н. Ченцовым [4]. Предполагается, что оцениваемая функция плотности вероятности fx) принадлежит гильбертову пространству L2 функций, интегрируемых по Лебегу с квадратом на всей числовой прямой [5]. В этом случае функция fx) представима в виде f (x) = «офо (x) - «1Ф1 (x) - «2Ф2 (x) - ...       (1)

где { ф _k } - полная ортонормальная система функций (базис) пространства L ₂; коэффициенты a _k находятся по формуле:

-X ^a k = ( f ', ф k ) = j f ^{( x} ) ф k ^{( x} ) ^dx .

-X

Проекционная оценка f N (x ) функции fx ) представляет собой N -ю частичную сумму ряда (1):

f N ( x ) = « о ф о ( x ) - « 1 Ф 1 ( x ) - ... - a N ф N ( x ).     (2)

Если восстанавливаемая функция f e L ₂, то при неограниченном увеличении N оценка (2) сходится к истинной плотности fx ) в среднем квадратичном:

Я1 ^f N ^- f l 1=0.

В [6] указано, что если, кроме того, функция fx ) является непрерывной и имеет ограниченное изменение, то оценка (2) сходится равномерно. Там же рассматривается оценка (2), в которой в качестве функций ф _k ( x ) взяты многочлены Эрмита. Работа [6] была выполнена при поддержке агентства NASA.

В работах [7; 8] рассмотрены некоторые обобщения оценки (2), имеющие вид

N fN (x) = ^X j a j ф j (x), j=o где весовые коэффициенты Xj выбираются из дополнительных соображений.

Однако требование f e L ₂ не выполняется уже для некоторых модельных законов распределения. Например, распределение % ² с числом степеней свободы 1 (т. е. распределение случайной величины, представ

ляющей собой квадрат нормально распределённой случайной величины с параметрами ц = 0 и о = 1) имеет плотность вероятности [9]

При этом

^{f ( x} ) =

x

V 2л

1 0,

_- 1

. 2

x >  0,

С1 гЛ .

f ²( x ) dx = —

dx

= -X,

x

т. е. f £ L ₂, следовательно, проекционная оценка плотности вероятности не сходится к fx ) в метрике пространства L ₂.

В работе предлагается построение сепарабельных гильбертовых пространств, являющихся расширениями пространства L ₂, в которых имеется возможность строить проекционные оценки функций плотности вероятности, не входящих в L ₂.

Определение и основные свойства пространства L ₂ , _w . Пусть w ( x ) - положительная измеримая функция. Определим пространство L ₂ , _w как множество действительных функций, для которых

-X j f 2(x)w(x)dx < -x .               (4)

-X

Для любых двух функций f, g e L ₂ , _w определено число

-X

^{( f} , g ) w = j ^{f ( x} ) g ^{( x} ) ^{w ( x} ) ^dx .            ⁽⁵⁾

-X

Действительно, для действительных функций fx ) и g ( x ) выполняется неравенство

I f ( x ) g ( x )| w ( x ) < 2 ( f ² ( x ) w ( x )

- g ²( x ) w ( x ) ) .

Поэтому из (4) следует, что интеграл в (5) принимает конечное значение. Очевидно, двухместный функционал (5) удовлетворяет аксиомам скалярного произведения. Причём условие (4) означает конечность нормы функции f, индуцированной этим скалярным произведением. Следовательно, пространство L ₂ , _w является гильбертовым. При w ( x ) = 1 пространство L ₂ , _w совпадает с пространством L ₂. Подбирая различные функции w ( x ), получим различные пространства L ₂ , _w , причём справедливо следующее утверждение.

Утверждение 1 . Если w 1 ( x ) <  w ₂( x ), то

^L 2, w ₂ ^{£ L} 2, w .

В частности, при w ( x ) <  1 пространство L ₂ , _w включает в себя пространство L ₂.

Доказательство. Утверждение следует из того, что если для функции f(x ) выполнено условие

-x

J f ² ( x ) w ₂ ( x ) dx < -x ,

-x то

-x-x

J f ²( x ) w 1 ( x ) dx <  J f ²( x ) w ₂( x ) dx < +x .

-x-x

Утверждение 2. Если для функций w 1 ( x ) и w ₂( x ) существуют такие константы m и M , что

,W

Vx е (-x; +x), 0 < m < —1--< M < +x, w2( x )

то пространства равны

^L 2, w = ^L 2, w ₂ .

Доказательство. Из условия теоремы следует, что w1 (x) < Mw2 (x), w2 (x) < — w1 (x). m

Тогда

-x-x

J f ²( x ) w 1 ( x ) dx <  J f ²( x ) Mw ₂( x ) dx =

-x

= M J f 2(x) w2(x)dx,(6)

-x

-x—x

J ^{f 2( x} ) ^w 2 ^{( x} ) d <  J ^{f 2( x} ) — w i ^{( x} ) ^dx = m

, -x

= — J ^{f 2( x} ) ^w 1 ^{( x} ) d m

-x

Из (6) следует включение L ₂ , w c L ₂ , w , из (7) -включение L ₂ w c L _{2 w} . Утверждение доказано.

Из утверждения 2 следует, что для фактического расширения пространства (т. е. для L2 w с L2 w ) необходимо, чтобы inf wytxl = 0, x w2( x )

или, что то же самое, w? (x) sup — = -x.

x w i ( x )

Заметим далее, что при таком расширении сохраняется различимость элементов, как показывает следующее утверждение.

Утверждение 3. Пусть w 1 ( x ) и w ₂( x ) - две измеримые положительные функции, f - функция, принадлежащая обоим пространствам L ₂ w и L ₂ w . Тогда

IIД > 0 ^1 К2 > 0

Доказательство. Пусть, напротив, при некоторых w 1 ( x ) и w ₂( x ) существует такая функция ^{f G L} Ц ^ ^L2w₂ , Л^{ля кото}р°Й

II4,> 0,                      (8)

но

II Я ₂ = ⁰

Тогда

J f ²( x ) w ₂ ( x ) dx = 0. -x

Так как подынтегральная функция неотрицательна, то отсюда следует, что она равна 0 почти всюду. Но w ₂( x ) всюду положительна, поэтому почти всюду равна 0 функция f ²( x ), из чего следует, что

J f ²( x ) w 1 ( x ) dx = 0.

-x

Получаем противоречие с (8), что доказывает утверждение.

Из утверждения 3 следует, в частности, что если две функции fx ) и g ( x ) принадлежат обоим пространствам L ₂ w и L₂ w , то они в этих пространствах одновременно различаются или нет:

II ^{f -} g ll w >⁰ ^1 l ^{f -} g l₂ >  0.

Оказывается, для любой функции плотности вероятности fx ) можно построить такое расширение L ₂ , _w пространства L ₂, которое будет содержать функцию f(x ).

Утверждение 4. Пусть f(x) - функция плотности вероятности некоторой непрерывной случайной величины. Тогда существует такая положительная измеримая функция w(x), что выполняется включение f е L2,w .

Доказательство. Как функция плотности вероятности, f(x ) интегрируема на всей числовой прямой, причём

J f ( x ) dx = 1.

-x

Тогда существует (конечный или бесконечный) интеграл

I = J f ²( x ) dx .

-x

При этом если I < +», то f е L ₂ , _w при w ( x ) = 1. Если I = +», то функцию w ( x ) можно построить следующим образом:

I — , f ( x ) >  1, w ( x ) = U ( x )                       (9)

[ 1,         f ( x ) <  1.

В силу измеримости функции f ( x ) множества

X 1 = { x е Ж | f ( x ) >  1} и X ₂ = { x е Ж | f ( x ) <  1} измеримы, поэтому измерима и построенная функция w ( x ). Кроме того,

J f ²( x ) w ( x ) dx = J f ²( x ) w ( x ) dx +

-x                   X 1

+ J f ²( x ) w ( x ) dx = J f ( x ) dx + J f ²( x ) dx ;

X ₂                  X 1           X ₂

J f ( x ) dx <  J f ( x ) dx = 1;

X i           —х

J f ²( x ) dx <  J f ( x ) dx <  J f ( x ) dx = 1.

X 2            X 2           —х

Таким образом, получаем, что

+х

J f 2(x)w(x)dx <+х, —х поэтому f е L2,w. Утверждение доказано.

Построение функции плотности вероятности, не принадлежащей данному пространству L ₂ , _w . Как показывает утверждение 4, для любой функции плотности вероятности fx ) можно построить содержащее её гильбертово пространство L ₂ , _w . Выбирая всё меньшие функции w ( x ), можно получать всё более широкие пространства L ₂ , _w . Однако не существует пространства L ₂ , _w , которое содержало бы всё множество функций плотности вероятности любых непрерывных случайных величин. Действительно, справедливо следующее утверждение.

Утверждение 5. Пусть w ( x ) - положительная измеримая функция. Тогда существует непрерывная случайная величина, у которой функция плотности вероятности fx ) такова, что

+х

J f ²( x ) w ( x ) dx = +х .

—х

Доказательство. Пусть w ( x ) удовлетворяет условию утверждения. Тогда существует такое £ > 0, что множество

A = {x е R | w(x) > £} имеет положительную меру. Определим на этом множестве функцию ф(x), обладающую свойствами:

J ф ( x ) dx <  +х , J ф ² ( x ) dx = +х .

A                 A

Заметим, что множество A может иметь весьма сложную структуру, в том числе быть нигде неплотным [10].

Так как система измеримых множеств пространства действительных чисел R является о-алгеброй, то любое множество положительной меры из этой системы можно представить в виде объединения счётного множества попарно непересекающихся его подмножеств положительной меры. В частности, для множества A имеем х

A = U A i ,       p A i >  0, А , - П A j. = 0 при i * j .

i = 1

Ряд, составленный из мер множеств A , очевидно, сходится, причём

х

E p A = P A .              (10)

n = 1

Обозначим через у n остаток ряда (10) после n -го члена:

х

У n E PA.

k = n + 1

Так как ряд (10) положительный, то согласно результату У. Дини [11, с. 319] ряд х      — 1

E p a у n ² 1 n = 1

сходится, в то время как ряд х EpA У 2—1 n =1

расходится. Используя это свойство, для каждого множества A _n построим функцию

Ф n ^{( x} )

У n ² 1 ,

0,

^{x е} A n , ^{x £} A n

и определим функцию ф ( x ) следующим образом:

Ф ( x ) = Е ф n ( x ).

n = 1

При этом

х

J ф(x)dx = E J Ф(x)dx =

A            n =1 An х              х     — 1

= E J ф n(x)dx = Epa у n 21 < +х;

n = 1 Д                  n = 1

A n

х

J ф ² ( x ) dx = E J Ф 2 ( x ) dx =

A              n=1 An х             х

= E J фП (x)dx = Epa у——1 =+х.

n = 1 Д                  n = 1

An

Функциюfx) будем искать в виде f (x) = <

Ф( x ) ky/w (x) 0, x е A, x £ A,

где коэффициент k определим из условия нормировки:

f f ( x ) dx = ¹C ^{ф (} x ) dx = 1.

—V     ^k Vw^x

Заметим, что интеграл в последнем выражении сходится, так как

Г Ф( x) 7 / 1f/\7., I . dx < —;= I ф(x)dx < +х.

! Vw(x)     V£ A

Тогда получаем k = J A

Ф ( x ) -J w ( x )

dx .

Таким образом, функция f ( x ) является функцией плотности вероятности некоторой случайной величины. При этом

'^x                       1     m ² ( x )

f f ( x ) w ( x ) dx = —- f----- w ( x ) dx =

-X                 k ² А ^{w ( x} )

+х

^{V f е L} 2 ^{( f} , g ) w = J ^{f ( x} ) g ^{( x} ) ^{w ( x} ) ^dx = ⁰

-x

= т m (x)dx = +».

^k A

Утверждение доказано.

Сепарабельность пространства L ₂ , _w . Как показывает утверждение 5, не существует некоего универсального гильбертова пространства, пригодного для оценивания любой мыслимой функции плотности вероятности. Кроме того, при рассмотрении пространства L ₂ , _w очень важным является установление его сепарабельности, так как в этом случае у этого пространства гарантировано существование счётного базиса и возможность представления любого элемента пространства в виде (1). Таким образом, если функция плотности вероятности принадлежит сепарабельному пространству L ₂ , _w , то её проекционная оценка сходится к ней. Рассмотрим следующую теорему.

Теорема. Пусть L ₂ с L _{2 w} . Тогда пространство L ₂ плотно в пространстве L _{2 w} .

Для доказательства этой теоремы сформулируем следующую лемму.

Лемма. Пусть h ( x ) - измеримая функция, ортогональная пространству L ₂:

V f е L 2 ( f , h ) = 0.

Тогда h ( x ) равна 0 почти всюду.

Доказательство. Пусть, напротив, h ( x ) ортогональна пространству L ₂ и отлична от 0 на некотором множестве А положительной меры:

ц А = ц { x е R | h ( x ) * 0} >  0.

Разобьём множество А на два подмножества

А ₁ = { x е R | h ( x ) >  0}, А ₂ = { x е R | h ( x ) < 0}..

Очевидно, что мера хотя бы одного из них положительна. Тогда из А ₁ или А ₂ можно выделить ограниченное подмножество положительной меры. Обозначим это подмножество через B . Очевидно, на множестве B функция h ( x ) сохраняет знак. Определим функцию f ( x ) следующим образом:

[ 1, x е B , x ) = 5                .

[ 0, x £ B .

Функция fx ) принадлежит пространству L 2 , и, кроме того,

( f , h ) = J f ( x ) h ( x ) dx = J h ( x ) dx * 0.

-x                B

Получаем противоречие с ортогональностью функции h ( x ) пространству L ₂. Лемма доказана.

Доказательство теоремы. Пусть, напротив, L ₂ не является плотным в L ₂ , _w . Известно, что для того, чтобы линейное многообразие М было плотным в гильбертовом пространстве H , необходимо и достаточно, чтобы в H не существовало ненулевого элемента, ортогонального всем элементам из М [12]. Отсюда следует, что в L ₂ , _w существует ненулевой элемент g , ортогональный пространству L ₂:

Из доказанной леммы применительно к h ( x ) = = g ( x ) w ( x ) следует, что функция g ( x ) w ( x ) равна 0 почти всюду. Так как w ( x ) > 0, то почти всюду равна 0 функция g ( x ), что противоречит тому, что g - ненулевой элемент пространства L ₂ , _w . Теорема доказана.

Из доказанной теоремы следует, что пространство L ₂ плотно в любом содержащем его пространстве L ₂ , _w . Тогда из сепарабельности L ₂ следует сепарабельность любого такого L ₂ , _w . В совокупности с утверждением 4 получаем, что для любой функции плотности вероятности можно построить проекционную оценку, сходящуюся в некотором пространстве L ₂ , _w .

Результаты численных экспериментов. Построим проекционную оценку плотности вероятности некоторых случайных величин, не принадлежащих пространству L ₂. Для этого с помощью формулы (9) построим весовую функцию w ( x ) и для соответствующего пространства L ₂ , _w построим ортонормиро-ванный базис методом ортогонализации Грамма-Шмидта [13]. Коэффициенты a _k в выражении (2) оценим по формуле [14]

^a k =- E m k ^{( x} i )^{w ( x} i ). " i = 1

Длину ряда N получим минимизацией значения wn -2jt»mk-i^mmk- k-0,....n,      (12)

n k = 0        k = 0

где m mk = ak =-jm k(xi)w(xi), n i=1

2     1 nbi„ smk = —7 Дтk(xi)w(xi)- mmk ) , n -1 i=1

которое является (с точностью до постоянного слагаемого) несмещённой оценкой функционала качества

Q {f}= M f - f

w оценки плотности вероятности [15].

Промер 1. Для функции (3) плотности вероятности случайной величины, подчинённой закону распределения / , функция w(x) имеет вид z х    V2^xг1, x е (0;0,139),

⁽ x ) = 5              ,               ,     v,

1,          clr-1.

Оценку будем строить на луче [0; +x), для чего в качестве системы линейно независимых функций возьмём последовательность е-x хр-x т2р-x х"р-x e , ^ve , ^v e , •••, ^v e , •••

После применения процесса Грамма-Шмидта был построен базис, несколько первых элементов которого имеют вид m0 (x) «1,482e-x, mi(x) ~ (-1,611 + 2,954x)e-x, m2(x) « (1,73 - 6,138x + 2,945x2)e-x,   ...

Оценка плотности вероятности строилась по независимой выборке случайной величины объёма n = 300. Оценки a _k коэффициентов, а также их оптимальные значения занесены в табл. 1.

В табл. 2 приведены значения IT N .

Из табл. 2 видно, что минимальное значение W N достигается при N = 15. График соответствующей оценки приведён на рис. 1.

Качество оценивания при этом составляет

' ^- /|[ . 0,045.

Пример 2. Рассмотрим непрерывную случайную величину, заданную следующей плотностью вероятности:

Квадрат этой функции не суммируем в окрестности двух точек x = 0 и x = 1, следовательно, / 6 L ₂. Построим содержащее эту функцию пространство L ₂ , _w . Для этого введём весовую функцию

4 V X ,

x е

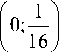
w ( x ) = <

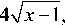
x е

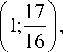
1, cir'I.

Построим проекционную оценку функции плотности вероятности в интервале (0; 2). Для построения базиса возьмём линейно независимую систему

	1 4Х	0 <  x <  1,
f ( x ) = 1	-тЦ	, 1 <  x <  2,            (13)
	4 V x -1
	0,	cir'I.

. л                       n л

1, cos x , cos л x , ..., cos     x ,

2                     2

и по независимой выборке этой случайной величины объёма n = 300 построим проекционную оценку плотности вероятности. Результат численного эксперимента приведён на рис. 2.

Таблица 1

Оценки (11) коэффициентов и их оптимальные значения при восстановлении плотности вероятности (3)

k	0	1	2	3	4	5	6	7	8	9
a k	0,633	-0,135	0,166	-0,117	0,104	-0,097	0,085	-0,066	0,051	-0,038
a k	0,636	-0,133	0,148	-0,1	0,088	-0,075	0,067	-0,061	0,056	-0,052
k	10	11	12	13	14	15	16	17	18	19
a k	0,033	-0,034	0,034	-0,031	0,028	-0,025	0,023	-0,029	-0,029	-0,03
a k	0,048	-0,045	0,042	-0,04	0,038	-0,036	0,034	-0,043	-0,043	-0,043

Таблица 2

Значения оценки (12) функционала качества при восстановлении плотности вероятности (3)

N	1	2	3	4	5	6	7	8	9
W N	-0,416492	-0,442569	-0,455039	-0,464734	-0,473139	-0,479536	-0,483056	-0,484753	-0,485328
N	10	11	12	13	14	15	16	17	18
W N	-0,485565	-0,485918	-0,486332	-0,486598	-0,486696	-0,486703	-0,48666	-0,48659	-0,486517

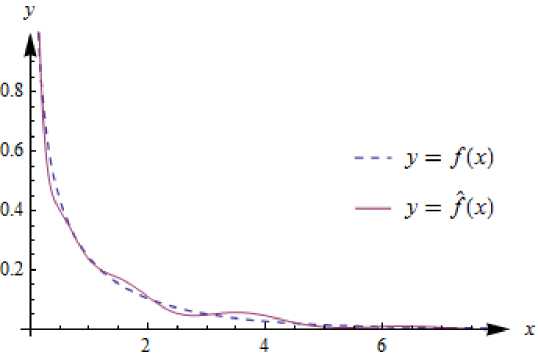
Рис. 1. Результат восстановления функции плотности вероятности случайной величины, подчинённой закону распределения % ² при k = 1

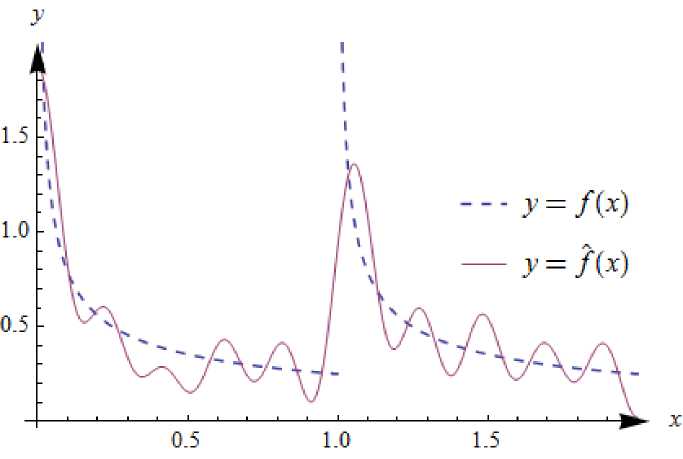
Рис. 2. Результат восстановления функции плотности вероятности случайной величины, подчинённой закону распределения (13)

Качество оценивания при этом составило

I f ^- f l С - ^01о2.

Наличие разрыва второго рода внутри области оценивания значительно ухудшило качество аппроксимации по сравнению с примером 1.

Заключение. Из доказанных свойств пространства L ₂ , _w следует, что для функции плотности вероятности любой непрерывной случайной величины можно построить проекционную оценку, сходящуюся в этом пространстве при определённом выборе весовой функции w ( x ). Численные эксперименты подтвердили, что предложенный способ оценивания плотности вероятности может быть использован в случаях, когда квадрат оцениваемой функции f ( x ) не суммируется, т. е. f 6 L ₂.