Выбор граничных условий к расчету параметров вихревого течения газодисперсных потоков

DOI:

Применяемые в настоящее время математические модели процессов газоочистки, как правило, сформированы на упрощенных теоретических представлениях о движении газодисперсных потоков. Они недостаточно учитывают режимные и конструктивные параметры аппаратов газоочистки, а также аэрогидродинамические свойства газодисперсных потоков. Эти модели не могут быть использованы для поиска оптимальных вариантов комплексных систем газоочистки, так как они показывают свойства объектов в узком диапазоне изменения параметров. Сложность общей гидродинамической картины сепарации многофазных потоков, а также взаимодействие этих потоков между собой, обуславливает трудности ее математического описания. Этим объясняется необходимость исследования влияния режимных и конструктивных параметров на эффективность процесса газоочистки с оценкой вклада отдельных элементов для более детального понимания физического механизма центробежной интенсификации [2]. Применение пакета вычислительной гидродинамики Ansys CFX позволяет рассчитывать с приемлемой для практики точностью гидродинамические характеристики вихревых течений на этапе разработки и проектирования промышленных устройств, позволяя избежать необходимости дорогостоящих натурных испытаний. Структура и механизм турбулентности, прямые и обратные токи в пограничном слое определяют специфические подходы к выбору граничных условий вихревого течения газо-взвеси [10, 11]. Проведенные расчеты позволяют определять потенциальные возможности динамического газопромывателя при использовании его в качестве аппарата для очистки газовых выбросов.

Задачи моделирования

Для грамотного выбора граничных условий и последующего исследования процессов, протекающих в вихревых центробежных аппаратах, необходимо определить связь между параметрами закручивающего устройства и формируемого им течения, поскольку численное моделирование трехмерных течений на сегодняшний день является проблематичным, данная задача сливается с известной проблемой характеристик закрученных течений и закручивающих устройств. Численный анализ течения газа внутри динамического газопромывателя [3] сводится к решению системы осредненных по Рейнольдсу уравнений Навье-Стокса:

¹ ^"( r P ^U r ^U r )+^"( r P ^U r ^U z ) = r d r            d r

1 d f   d u _r )   d f    d u r )    d P      pu r   puФф

—  1 ГU- T ----- I +1 Г U t ----- I P t т 1

r d r I      d r J   d z I      d z J    d r       r ² r

7 d r ( ^{rpuu )+} d z V^pu^ ) =

1 r

d f    ^{d u} Ф Y d f    ^{d u} Ф )

I rpT        I +I rpTI dr ^     dr J dz ^

ρυ_ϕ µ T _r

ρυ_ϕυ _r r

1 ^( rPu,uz )+^(rPuzuz) r dr

1 r

d f   du )  d f

— I rpT —- I +--1 rpT —- dr (    dr J dz ( dP dz

где u _z - скорость потока вдоль оси; u r - скорость потока в радиальном направлении; и_ф - тангенциальная скорость потока; р - плотность смеси; ц' Т - коэффициент турбулентной вязкости; Р – давление; и' - вектор скорости.

Для замыкания газодинамических уравнений Навье-Стокса использовалась стандартная (k- e ) - модель турбулентности. Для нахождения скалярных параметров к и e используются два дополнительных модельных уравнения, содержащих эмпирические константы [4]. Расчетная сетка была построена в сеточном генераторе Ansys CFХ . Большинство задаваемых граничных условий могут быть сведены: к условиям первого рода (задано значение функции), к условиям второго рода (задан градиент функции по нормали к границе) или к условиям третьего рода (задается линейная комбинация значений функции и нормальной производной). Постановка граничных условий оказывает существенное влияние не только на устойчивость, но и на точность решения конечно-разностного уравнения. Изучению граничных условий на конечной расчетной сетке посвящены работы [5– 7], в частности, в [7] показано, что при больших числах Рейнольдса из-за неправильно поставленных граничных условий ошибка на границах может вдвое превышать ошибку аппроксимации во внутренних точках. В работах [8–10] представлены результаты экспериментальных исследований центробежных пылеуловителей со следующими параметрами: число Рейнольдса варьировалось от 1∙10² до 60∙10⁴; параметр закрутки изменялся в пределах К =0 ^ 4. Проведем расчет течения для динамического газопромывателя и сравним полученные решения с экспериментальными данными.

Постановка граничных условий

Граничные условия, удовлетворяющие уравнениям переноса в областях R >  r , должны записываться с учетом равенства потоков частиц на радиусе r , а также равенства самих концентраций частиц на радиусе R . Вблизи ограничивающей поверхности тангенциальные скорости газа уменьшаются и принимают нулевое значение на поверхности. Центробежные силы, действующие на мелкие частицы, также уменьшаются и принимают нулевое значение на самой стенке. Частицы вблизи стенки увлекаются турбулентными пульсациями и отходят от стенки, а центробежными силами возвращаются к стенке. Таким образом, вблизи неподвижной поверхности частицы находятся в динамическом равновесии, на границе поток

– твердая стенка, перенос частиц отсутствует, и суммарный поток частиц за счет центробежных сил и диффузионного переноса должен быть равен нулю. На оси газопромывателя, вследствие симметрии течения, производная по радиусу от концентрации частиц равна нулю. В расчетной сетке твердую стенку представляют границы Г1, Г3, Г4, Г5 (рис.1).

Так как линии Г₁ – Г₈, и Г₃ – Г₄являются линиями тока, то на этих стенках функция тока y может принимать любое постоянное значение. По характеру течения для Г₁, Г₅функция тока y = 0; для Г₃, Г₃ ^/ функция тока y = y _{max .}

Границы Г4и Г6 представляют выходное сечение или проницаемую стенку. Если на Г1, Г3, Г8 выполняется условие прилипания

Uz = иф = Ur = 0, то на Г4 и Г6 изменение скорости можно задать некоторой функцией f(r).

Тогда dU       V max

Uz = Uz (r) ^f = 0, f dV = [Pr^ (rdr(1)

dX      0       r=L

Особенно важно определить значение вихря на стенке. На примере твердой стенки Г₃ рассмотрим вывод граничного условия первого порядка точности для вихря y . В окрестности точки разложим функцию y в ряд Тейлора

Но ^{(d v} / ^{d r} P ) p = 0, м ^-^ , так как' u_z = u = 0 ■         5 r                 z ^r

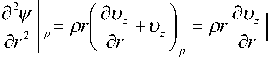
Подставляя d y / dr, d² y / dr² в (2) и решая его относительно w _i,j, где компонента w _i,j, характеризует вращение частиц потока относительно оси, которая имеет форму окружности (кольцевой вихрь), с учетом w _i,j = 0, находим

®r=^- — ^гт ^{+ o (a} r ) (3) p r A r ⁷

Независимо от ориентации стенки и от значения y на границе можно записать

= - 2 ( ^y _{г+ 1} y r ) _{+ 0} ( a n )

2, где Dn – расстояние по нормали к стенке от ближайшего узла. Для получения условия второго порядка точности продифференцируем выражение, определяющее вихрь w, ce.>   =9гиг   d 2uz = dr p  dzdrd d dur _ £ Г1 d3v - 1 d 2v + 1

dz dr p r dr3 r2 dr2 r3d

Sy 1 d 2v vu+i = vi. +^r pAr + 2"r2 pAr

+1      Arr ³+ 0 ( a r ⁴ )

6 d r³ p ^v ’

Из уравнения неразрывности

Su.    du u           du     du

—L = z_ - _r ■ u r = 0 ^ —L = z d r d z r             d r d z

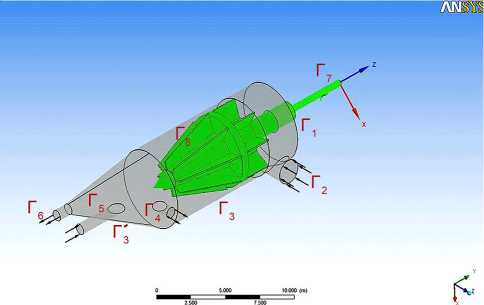
Рис. 1. Схема к расчету граничных условий модели

Если представить стенку как плоскую пластинку гр®¥, то ди _ д2uz I    1 d3v д2uz _ о dr p_-lzrIp -pr"dr3" p,lZr~ в силу условия прилипания. Отсюда следует, что d® _- 1 dv; d3V| _- p ®M - mt дr p    pr дr3 ’ д r3 'p           A r dv\ д2v I d3v i

Подставим p , p , p в выраже- д r ¹ д r ¹ д r ¹

ние (2).

Получим

1                     2 1 |          ® i £ + 1 ^ i I 3

v^ i + x ^_ v i £ ⁺ 2 ( - p ^r ® ., _t ^{)A r +} 6 I ^- pr ’ _A r ’ l ^{A r} .

Или принимая, что A n = A r , а точка с индексами i, j является граничной, имеем

® г

³ ( ^V г+1   ^V г ) + ® г+1

rp A n ²      2

Если ряд Тейлора для функции у продолжить до членов четвертого порядка, то учитывая, что r_p ®¥ , и d у / dr =0

® F q 1 ⁺ q 2 ® F+1                  ⁽⁷⁾

Граница Г₇ представляет собой ось симметрии. Для Г 7 имеем u _r , и _ц=0 , поэтому ( d u r / dz)= 0. Расходная скорость симметрична относительно оси ( d u _z / dz)= 0, откуда w _r=0.

Условия на входом патрубке Г₂ нельзя записать однозначно. Они будут меняться в зависимости от физической картины течения в исследуемой области. Первый подход к постановке граничных условий на входе: полностью задать значения у и w . Например, Г 2 : w =0 (принять допущение о потенциальном характере течения); зная величину расхода:

Q _ 2 n rl р г|                  (8)

можно определить среднее значение радиальной скорости

U ’l^_ U ."I;

и задать линейную зависимость для функции тока

V ^_ V max • ^Z / l ,

где z – текущая координата ввода частиц; l – ширина входного патрубка.

V , £ +1 — ^V i , £ _ 1

A r ² p    ²

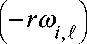
I

+

⁺ 6

(

^{— r}

V

ω г, £ +1

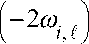
A r

— ® i, £

A r +

A r ²

^{A r +} "24

(

— r

д ² ю ' д r ² ,

A r ² (_ з ^ i , £ +1 - ^ i , £ I

24 ³     A r

V                    7

Формула для вихря на твердой границе примет вид

На динамику течения наибольшее влияние оказывает профиль входной скорости, чем закон изменения функции тока, из которого определяется величина скорости. Автор [11] в качестве условия на входной границе задавал равномерный поток u = const , в других источниках [7, 8] рассматриваются профили Блазиуса или Пуазейля. Для правильной постановки условий на входе необходимо путем проведения численного эксперимента оценить влияние того или иного профиля скорости на характер течения. Тогда величина w _r находится по значению d u r / dz по уравнению

_ dur I  I 82v дz p    pr dz2

— ^{V г- 2} 2 ^V ₂ ^{г- 1 + V г} (10)

ю _г

v г ^- V г+1

_A 2 ( r 5A r A n p - +--

V 3   24

В [11] предложено записывать формулу (6) как

На выходной границе Г₄наиболее надежным способом задания краевых условий является полная определенность значений у , w , u . Для скоростей здесь также могут быть

предложены равномерный или параболический профили, для вихря – потенциальный сток w=0. В некоторых задачах при течениях в каналах различной конфигурации применяется постановка «мягких» граничных условий дю dy

= 0,   = 0 ^ y = y , ю = ю

Г Г—1 Г        Г—1

дz     дz аю = au r=о a2y =о                (11)

a z ""аТ" ’ а¥ " "

Эти условия имеют второй порядок точности.

На вершине угла выхлопного патрубка выполняется условие прилипания, это конечная точка твердой стенки, u _z, u _r, u _ц, y =0. Для определения ω в этой точке можно воспользоваться формулой (4):

У а - У г a шг                2 , pr ^ П

2 A z ²      A z (12)

A n = ( A r cos в ) =---- ;Y Y = —

1 + y 2     Ar где b – угол наклона конической части аппарата.

Для модели [12], было проведено интегрирование методом Рунге-Кутта в окрестности каждого узла конечно-разностной сетки, которой покрыто все пространство газопромывателя. Каждый узел сетки определяется значения- ми проекций скорости потока: радиальной ur,тан-генциальной uц , осевой uz. Переходы между узлами выполняются скачкообразно путем замены одного значения скорости другим или нахождением промежуточных значений между узлами с помощью интерполяции. Особенность такой постановки краевой задачи состоит в том, что условие прилипания реализуется на каждом временном шаге. При этом существенно, что условие прилипания и условие для функций y и w ставятся на разных границах, так как использование этих двух условий по одной и той же границе модифицирует нашу задачу, и при численном решении может привести к снижению точности. По результатам вычислений строились картины линий тока и профили скорости в различных сечениях потока.

Анализ результатов численного решения краевой задачи

Для решения поставленной задачи по схеме продольно-поперечной прогонки была разработана расчетная программа. По результатам вычислений были получены профили осевой и окружной компонент скорости (рис. 2).

Картина течения газопылевого потока в динамическом газопромывателе является достаточно сложной ввиду того, что в центральной части аппарата расположен лопастной завихритель. Анализ гидродинамики и распределения осаждаемых частиц в динами-

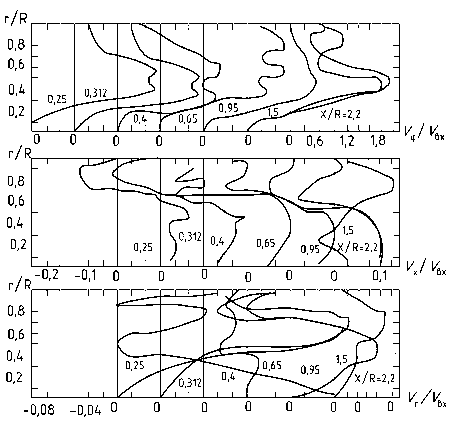
Рис. 2. Проекции тангенциальных, осевых и радиальных скоростей вдоль аппарата в сечениях х/R = 0,25; 0,312; 0,4; 0,65; 0,95; 1,5; 2,2 при значениях параметров: V _г / V _вх = 0,01;V _j / V _вх = 1,8; Re = 5∙10⁴

ческом газопромывателе показал, что из-за наличия турбулентной диффузии, частицы концентрируются у стенки аппарата не плотным слоем, а в виде разрыхленного концентрированного газопылевого слоя. При этом на стенке не образуется осыпающийся слой, а пыль локализуется в кольцевом пристенном слое определенной толщины в виде спиральных пылевых скоплений в форме жгутов. Инициатором образования спиральных пылевых жгутов является лопастной завихритель. При прохождении пыли через лопатки завихрителя происходит концентрирование частиц на периферийной зоне лопаток. Таким образом, однородный поток после прохождения лопастного завихрителя разделяется на ряд параллельных потоков с чередующейся то обедненной, то обогащенной концентрацией пыли. Толщина и плотность пристенного слоя зависят от скорости газа, угла закрутки, характера ввода потока в динамический газопромыватель. Более высокие скорости способствуют уменьшению толщины пристенного слоя, несмотря на возрастающую при этом роль турбулентной диффузии. Положение центра вращательного потока не совпадает полностью с геометрической осью аппарата, то есть имеет место определенный незначительный экс-цен-триситет, величина которого не превышает 8– 10 % от радиуса аппарата. Наличие подобного эксцентриситета закрученного потока отмечаются также исследователями [7].

Учитывая, что величина эксцентриситета незначительна в исследуемом аппарате, а в его центральной части расположено оросительное устройство, будем рассматривать течение газового потока как симметричное относительно оси аппарата. Отметим, что профиль окружной скорости uj существенно изменяется по радиусу газопромывателя и по оси х, что означает наличие дифференциального вращения, вследствие чего вихревые линии начинаются закручиваться по спирали, как показано в работе [12]. На рисунке 3 представлены линии окружной скорости, видно, что вблизи стенок образуются вихревые зоны.

Для тангенциальной скорости характерен дрейф максимума от периферии к центру и сокращение зоны вынужденного вихря. Тангенциальная скорость значительно больше осевой в пристенной и квазипотенциальной зонах, а в области оси практически одного с ней порядка. Осевая составляющая практически не меняет своего профиля, ее максимум находится вблизи стенки аппарата.

Разработанная модель помогает быстро и наглядно смоделировать движение запыленного газового потока с учетом внесенных в геометрию аппарата изменений. Таким образом, модель может применяться для оптимизации конструкции динамического газопромывателя.

Выводы

• 1.    Был разработан алгоритм моделирования процесса сепарации дисперсной фазы в газовом потоке. Проведенные расчеты позволяют определять потенциальные возможности динамического газопромывателя при использовании его в качестве аппарата для очистки газовых выбросов. Верификация полученных расчетом данных проводилась путем моделирования процесса течения газожидко-

  

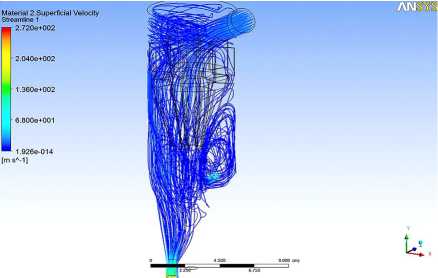
  Рис. 3. Проекции окружной скорости газодисперсного потока

  
  

• 2.    Расчеты течений, определяемые краевой задачей, проводились для значений чисел Рейнольдса от 1 • 10² до 60 • 10⁴. По результатам вычислений строились картины линий тока и профили скорости в различных сечениях газопромывателя. Анализ полученных профилей скорости позволяет выявить три характерные области по оси аппарата: область формирования газового потока, область стабильного потока и область демпфирования.

• 3.    Изменяющаяся закрутка потока может вызвать появление вблизи стенок газопромывателя зон обратного тока, снижающих эффективность сепарации тонких фракций пыли. Для уменьшения влияния возвратного течения можно оптимизировать соотношение высоты и ширины тангенциального ввода. Конический завихритель также оказывает демпфирующее действие на газодисперсный поток, при этом происходит трансформация профиля скоростей.

• 8.    Усманова, Р. Р. Обобщение зависимостей между режимно – конструктивными параметрами, структурой потоков и интегральными характеристиками вихревого аппарата / Р. Р. Усманова, В. С. Жернаков // Вестник УГАТУ. – 2010. – № 2. – С. 51–55.

• 9.    Шаров , С. В. Выбор граничных условий во входном сечении трубы при расчете закрученных течений / С. В. Шаров, С. Г. Черный, В. Л. Окулов // Теплофизика и аэромеханика. – 1997. – Т. 4, № 3. – С. 347–350.

• 10.    Menter, F. R. Advanced Turbulence Modelling in CFX / F. R. Menter, T. Esch. – CFX Update – Spring. – 2002. – № 20.– P. 4–5.

• 11.    Vasilyev, A.V. Valve Cam Design Using Numerical Step-By-Step Method / A.V. Vasilyev, Yu. S. Bakhracheva, O. Kabore // Вестник Волгоградского государственного университета. Серия 10, Инновационная деятельность. – 2014. – № 1. – С. 26–32.

• 12. Wilcox, D. C. Turbulence Modeling for CFD / D. C. Wilcox. – DCW Industries, Inc., La Canada, California,1993.

• 13. Xia, J. L. Numerical and Experimental Study of Swirling Flow in a Model Combustor / J. L. Xia, G. Yadigaroglu, Y. S. Liu. – Int. Journal of Heat and Mass Transfer, 1998. – Vol. 41, № 11. – P. 1485–1497.

стного потока в пакете вычислительной гидродинамики Ansys CFX .

СПИСОК ЛИТЕРАТУРЫ вателе / Р. Р. Усманова, В. С. Жернаков // Вестник УГАТУ. – 2013. – Т. 17, № 2. – С. 63–67.