Выбор характеристического полинома двоичной м-последовательности для идентификации нелинейного динамического объекта

Для идентификации нелинейных динамических объектов используются их различные модели, в том числе и отрезок ряда Вольтерра, в дискретном случае имеющий вид:

N -1 Q -1 Q -1

Xi ] = h o + A t • Z h[ j' ] • x [ i - j ] + A t ² • У\ h[k , l ] • x [ i - k ] • x [ i - l ] , j =0 k l

(1) здесь y[i] – реакция объекта, Δ t – шаг дискретизации, x[i] – входной сигнал, h₀, h[j], h[k,l] – ординаты ядер Вольтерра N, Q – времена памяти ядер первого и второго порядков [1].

На практике для независимой оценки ординат ядер Вольтерра при идентификации применяют ортогональные к сдвигу кусочно-постоянные тест-сигналы небольшой амплитуды, не нарушающие нормальное функционирование объекта, тогда при измерении реакции объекта один раз на такте тест-сигнала:

h [ j ] =

p

Z У [ i ] • x [ i - j ] i = 0

p

Z X ² [ i - j ]

i = 0

Z y [ i ] • X [ i - k ] • X [ i - 1 ] h[ k , l ] = ^^ ^^------------------------

Z x ² [ i - k ] • x ² [ i - 1 ] i = 0

Здесь р – число замеров, размерность плана эксперимента.

Для моделей динамики используют субоптимальные композиционные планы эксперимента с ядрами в виде планов Плакетта-Бермана или двоичных (троичных) М-последовательностей [1,2]. В композиционных планах эксперимента для моделей динамики строки ядра плана соответствуют двоичным числам, появляющимся в регистре сдвига аппаратного или программного генератора М-последовательности на каждом такте.

Отметим, что в литературе имеется недостаточно сведений о практической стороне синтеза субоптимальных тест-сигналов на основе М-пос-ледовательностей с использованием современных аппаратных и программных средств. Цель этой статьи частично восполнить этот пробел путем разработки алгоритма и программы для отбора двоичных М-последовательностей с необходимыми корреляционными свойствами, пригодных для использования в тест-сигналах.

Двоичная М-последовательность является упорядоченным с помощью сопровождающей матрицы (характеристического полинома F(x)), множеством компонент Si вектора координат элементов поля Галуа GF(2n) в степенном базисе [4]. М-последовательность, генерируемая с помощью характеристического полинома степени n, имеет период (2n – 1) такт.

При генерации тест-сигналов эти компоненты заменяются реальными сигналами с нормированными значениями:

х(0) = +1; х(1) = -1. (3)

Умножение для реальных сигналов оказывается эквивалентным сложению по модулю 2 для компонент Si:

1 ⊕ 0 = 1 (-1)·(+1) = -1

• 1    ⊕ 1 = 0 (-1)·(-1) = +1 (4) 0 ⊕ 0 = 0 (+1)·(+1) = +1

0 ⊕ 1 = 1 (+1)·(-1) = -1

Для независимой оценки ординат h0 и h[k, k] в тест-сигнал на основе двоичной М-последова-тельности вводятся дополнительные такты, после чего полный факторный композиционный план содержит (2n+2n+1) строк, а тест-сигнал -(2n+2n+4N-3) тактов [2]. Дополнительные такты необходимы также для устранения погрешности от неверного задания исходного состояния объекта перед началом тестирования. В качестве примера на рис. 1 приведен композиционный сигнал на основе двоичной М-последовательности с характеристическим полиномом F(x) = х3+х+1, ам-

Известия Самарского научного центра Российской академии наук, т. 13, №4, 2011

fx(t)

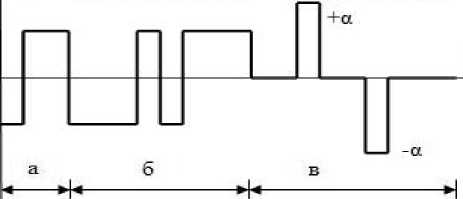
Рис. 1. Композиционный сигнал на базе двоичной М-последовательности: а – формирование начальных условий, б – ядро плана, в – дополнительные такты для оценки h₀ и h[k, k]

плитуды дополнительных импульсов а определяются по параметрам плана, точками указаны моменты измерения реакции объекта [2].

М-последовательности с запаздыванием j>n являются линейными комбинациями последовательностей с запаздываниями в диапазоне (1 ^ n) того же характеристического полинома:

• S i — = 3 1 .5, 1 ф аД © a^S n      (5)

Коэффициенты aiв (5) совпадают с коэффициентами полинома-остатка Rj(x) в GF(2n) [4]:

Rj(x) = xj mod F(x).            (6)

Выражение (6) иногда называют алгоритмом Дэвиса, его применяют для генерации задержанных М-последовательностей при идентификации линейных динамических объектов.

В специализированной литературе имеются таблицы коэффициентов полиномов различных степеней для генерации М-последовательностей. Нужно выбрать полином, обеспечивающий раздельную оценку ординат h[j] и h[k,l] при наи- меньшей длине тест-сигнала и известных временах памяти ядер Вольтерра N и Q.

Комбинированный тест-сигнал на базе М-последовательности длиной (2n – 1) тактов позволяет раздельно оценивать по (2) n ординат ядра первого порядка и (n·n) ординат ядра второго порядка. Для большинства реальных динамических систем N > Q, поэтому выбираем разрядность n полинома F(x) так, чтобы значимые ординаты ядра h[k,l] полностью размещались в квадрате n·n. Если нужно произвести идентификацию динамического объекта со временем памяти ядра Вольтерра первого порядка большим n, потребуется генерировать реплики М-после-довательности с запаздыванием j>n и изменить параметры дополнительной части тест-сигнала.

При использовании запаздывания j>n оценки ординат h[j] и h[k,l] могут оказаться смешанными в силу (5), если:

х[i-j] = x[i-k]·x[i-l]. (7)

Алгоритм для отбора характеристических полиномов М-последовательностей состоит в том, что по (6) определяем максимальное запаздывание j>n, при котором в полиноме-остатке не менее трех ненулевых коэффициентов, то есть оценки h[j] и h[k,l] не связаны. Из нескольких полиномов F(x) одной степени выбираем полином с максимальным значением допустимого запаздывания.

Процесс идентификации связан с автоматическим управлением объектом исследования, оборудованием для подачи тест-сигнала и сбора данных, обработкой данных. Это удобно осуществлять в специализированной среде программирования LabVIEW [5]. Разумно и подготовительную работу делать в той же среде. Автором был

Рис. 2. Блок-схема виртуального прибора для определения максимального запаздывания М-последовательности.

области определения ядра первого порядка отличаются значительно, таким образом отбор характеристических полиномов М-последовательнос-тей для синтеза эффективных композиционных тест-сигналов для идентификации нелинейных динамических объектов является обязательным.

ВЫВОДЫ

При заданной области определения ядра Вольтера второго порядка h[k,l] в квадрате n·n максимально допустимые значения запаздывания тест-сигнала на базе двоичной М-последо-вательности (область определения ядра h[j])

Таблица 1. Результаты расчета допустимого максимального запаздывания для некоторых характеристических полиномов

Коэффициенты полинома F(x) Степень полинома F(x) Период М-последовательности Максимальное запазды вани е 111000011 8 255 54 110101001 8 255 14 110001101 8 255 60 111110101 8 255 14 111100111 8 255 116 11100100001 10 1023 126 11011000001 10 1023 40 11010001001 10 1023 58 11110110001 10 1023 282 111000000000101 14 16383 1631 110101000000001 14 16383 578 111110100000001 14 16383 612 111110000000101 14 16383 930 разработан несложный виртуальный прибор для определения допустимого запаздывания в среде LabVIEW по изложенному выше алгоритму. На рис. 2 представлена блок-схема виртуального прибора, на рис. 3 – лицевая панель.

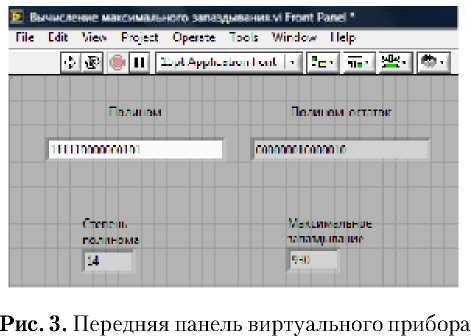
В окно “Полином” лицевой панели прибора вводятся в двоичном коде коэффициенты характеристического полинома, для GF(2n) это обычное представление F(x). Запускается виртуальный прибор (рис.3), определяющий полином-остаток, максимально допустимое число ординат в h[j] без смешивания оценок h[j] и h[k,l].

Результаты расчета для некоторых характеристических полиномов приведены в табл. 1, они подтверждают, что для различных характеристических полиномов одинаковой степени допустимые сильно различаются для различных характеристических полиномов одинаковой степени n. Предложенные в статье алгоритм и программа позволяют отбирать характеристические полиномы М-последовательностей, приводящие к генерации тест-сигналов наименьшей длины.