Выбор конструктивных параметров веретен

В связи с высокими скоростями вращения шпинделей веретен большинство шпинделей работает в зоне между первой и второй критическими скоростями. Поэтому при разработке веретен обязательно проводится определение собственных частот колебаний шпинделя для оценки правильности выбора его конструктивных параметров

Исследованиями установлено, что блочек шпинделя ввиду близости места его крепления к верхней опоре заметного влияния на собственную частоту шпинделя не оказывает. Шпиндель веретена без блочка приведен на рис.1. Как видим, его конфигурация довольно сложная. Для определения первой собственной частоты можно шпиндель считать невесомым, приведя часть его массы ( m пр ) к концу шпинделя. Тогда мы получим расчетную схему невесомого шпинделя с сосредоточенной массой m пр на конце. Зная коэффициент влияния δ 11 , численно равный деформации шпинделя в месте расположения m пр от единичной безразмерной силы, найдем жесткость шпинделя в этом месте к = 1/ δ 11 .

Таким образом мы можем при малых колебаниях рассматривать вместо невесомого шпинделя с массой mпр на конце стандартную колебательную модель, изображенную на рисунке 2. Для этой модели запишем уравнение движения ткр у + ку = 0. Решение этого уравнения, как известно, имеет вид y = Asin (pt+ϕ), где A и ϕ - произвольные постоянные интегрирования,

p

к mпр

^m п р ^δ 11

собственная круговая частота колебаний

невесомого шпинделя с массой m пр .

По исследованиям Я.И.Коритысского для веретен со сферической втулкой m пр = 0,313 m , где m - масса консольной части шпинделя без блочка. Отсюда видно, что если нам известен коэффициент влияния δ 11 и размеры шпинделя, то можно определить первую собственную частоту шпинделя без паковки.

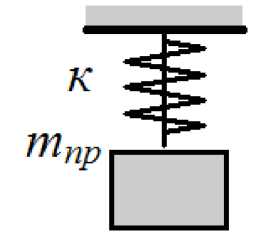
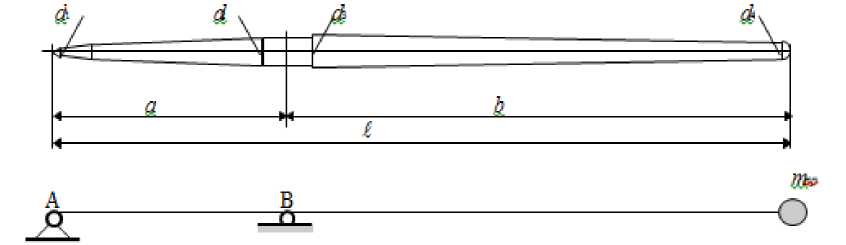
Рис-1.Шпиндель вретена.

Рис-2.динамическая модель шпинделя

Результаты расчета сравниваются с заданным диапазоном рабочих скоростей шпинделя. При этом может быть два варианта : либо ω max ≤ 0,7 p ; либо ω min ≥ 1,4 p , т.е. шпиндель должен работать либо в дорезонансной, либо в зарезонансной зоне. Если эти условия не выполняются, то параметры шпинделя (диаметры характерных сечений, расстояние между опорами) должны быть изменены.

Широкое распространение на кольцепрядильных машинах получили веретена типа ВН. Массой шпинделя по сравнению с массой насадки m пренебрегаем и считаем, что невесомый шпиндель с тяжелой насадкой вращается в жестких опорах.

Так как жесткость насадки примерно в 10 раз больше жесткости шпинделя считаем далее насадку абсолютно жесткой. При вращении шпинделя возникают сила инерции , максимальное значение которой можно подсчитать по формуле Pи = m ω2 ys и гироскопический момент, величина которого определится по формуле M г = - (I 0 - I э) ω2 (ϕ1+δ cosε ), приложенные в центре тяжести насадки.

Здесь y s = y 1 + e + ( ф 1 + 8 cos s ) 4 , s -угол, составляемый плоскостью, содержащей угол δ , с плоскостью чертежа (в наиболее неблагоприятном случае ε = 0), I 0 , I э моменты инерции массы насадки относительно главных центральных осей инерции насадки (относительно продольной оси - I 0 и относительно поперечной оси - I э , проходящих через центр S тяжести насадки).

Уравнения для подсчета прогиба y1 и угла ϕ1 поворота сечения шпинделя в точке крепления насадки от силы Pи и момента M г , приложенных в центре S тяжести насадки, можно записать, используя метод сил y1 = δ1S Pи + δ11 M г ,       ϕ1 = δ 2S Pи + δ 22 M г ,  (1)

где δ 12 - коэффициент влияния, численно равный прогибу в сечении шпинделя от безразмерной силы; P = 1, приложенной в центре S тяжести насадки, δ 2S - коэффициент влияния, численно равный углу поворота сечения шпинделя от то же силы, δ 12 и δ 22 - аналогичные коэффициенты влияния от действия безразмерного момента M = 1.

В результате мы получим силу P = 1 и момент M p = 1 х 4 .

Тогда δ 1S будет складываться из прогибов шпинделя в сечении 1 от силы P = 1 и момента M p = 1х 4 , приложенных там же, т.е.

8 is = 8 11 + M p 8 12 = 8 21 + 8 22 4 .  (2)

Рассуждая также, можем записать

8 2s = 8 21 + M p 8 22 = 8 21 + 8 22 4 ,  (3)

где δ 12 - коэффициент влияния по углу поворота сечения 1 шпинделя. от силы P = 1, приложенной там же ( δ 12 = δ 21 ).

Подставляя в уравнения (1) выражения P и и M г и проводя преобразования, получим систему двух линейных неоднородных алгебраических уравнений относительно y 1 и ϕ 1

A y 1 + F ω ² ϕ 1 = N, C y 1 + D ϕ 1 = M , (4)

где A = m 8 1s о ² - 1 ; F = m 8 1s 4 - (I o - 1 э ) 8 12 , C= m 8 2s co² ,

D = ( m 8 2s I s - (I o - 1 э ) 8 22 ) o ² - 1, N = [ - m 8 1s e + ((I o - 1 э ) 8 12 - m 8 1s ^_s ) 8 cos s ] or , M = [ - m 8 _2s e + ((I_o - 1_э ) 8 ₂₂ - m 8 _2s 4 ) 8 cos s ] or .

Определитель этой системы

Δ ( ω ² ) =

A

C

F ω ²

= A D - C F ω ² .

Если подставить сюда выражения A, B, D, F, то будем иметь

A ( o ² ) = - m B H or - [ m ( 8 1s + 8 2s 4 ) - B 8 22 ] o ² + 1,  (6)

где H = δ 12 δ 2S - δ 1S δ 22 , B = I 0 - I э .

Значения деформаций шпинделя для заданных параметров системы и частоты его вращения можно подсчитать y1 =

1N

Δ ( ω ²) M

F ω ² D

ND-MF ω ²

Δ ( ω ²)     ^,

1 AN

ϕ ¹ = Δ ( ω ²) C M

AM-CN

Δ ( ω ²)   .

Очевидно, что если Δ(ω2 )→ 0, то  y1 и ϕ1 будут стремиться к бесконечности. Приравнивая знаменатель нулю, получим уравнение

Δ ( ω ² ) = 0 (7)

для определения двух собственных круговых частот изгибных колебаний шпинделя.

Вторая собственная частота, как правило, лежит далеко за пределами рабочих частот вращения шпинделя. Наименьшее значение рабочей частоты ω вращения шпинделя должна быть больше его первой собственной частоты ω 1 . Для максимальной рабочей частоты шпинделя можно подсчитать y 1 и ϕ 1 , а затем

P и = m (y 1 + e + ( Ф 1 + 5 cos £ ) 4 ) w ² ,     (8)

M г = - (I 0 - I э ) ( ϕ 1 + δ cos ε ) ω ² .            (9)

По этим ориентировочным значениям P и и M г , приложенным в центре S тяжести насадки, можно легко оценить реакции в опорах шпинделя.