Выбор материалов для «ахроматизации» рельефно-фазовых дифракционных структур

Зависимость дифракционной эффективности (ДЭ) дифракционных оптических элементов от длины волны в ряде случаев существенно ограничивает эффективность использования таких элементов. Преодолеть указанное ограничение позволяет предложенное в 1985 г. А.В. Лукиным, К.С. Мустафиным и Р.А. Рафиковым решение, позволяющее выровнять с той или иной степенью точности ДЭ в заданном спектральном диапазоне [1]. Это решение, предполагает построение многослойных и, в частности, двухслойных рельефно-фазовых микроструктур. Аналогичные решения предложены и в ряде других более поздних работ, см., например, [2, 3]. На практике многослойные структуры для выравнивания ДЭ впервые использованы фирмой Canon в новых телеобъективах [4].

ДЭ работающей на просвет рельефно-фазовой микроструктуры зависит от величины фазового сдвига, вносимого в проходящую волну. В случае двухслойной микроструктуры величина фазового сдвига определяется выражением

Ik

∆ϕ(λ) = 2π h∆n(λ), (1) λ где h - высота микрорельефа; λ - длина падающей волны; ∆n - разность показателей преломления двух слоев микроструктуры на длине волны λ (рис. 1).

Из выражения (1) видно, что фазовый сдвиг а, следовательно, и ДЭ не будут зависеть от длины волны, если разность показателей преломления двух слоев микроструктуры окажется линейной функцией длины волны вида

∆ n ( λ ) = b λ , (2)

где b - величина, независящая от длины волны.

Решение, направленное на подавление зависимости ДЭ от длины волны за счет построения структуры из нескольких слоев универсально в том плане, что положительный эффект не зависит от закона изменения пространственной частоты структуры по поверхности дифракционного оптического элемента. Следовательно, это решение применимо для «ахро-матизации» элементов любого типа и, в частности, таких как дифракционные решетки, дифракционные линзы и фокусаторы.

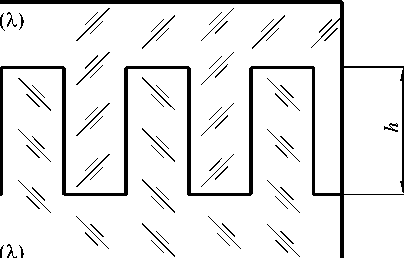
а

б

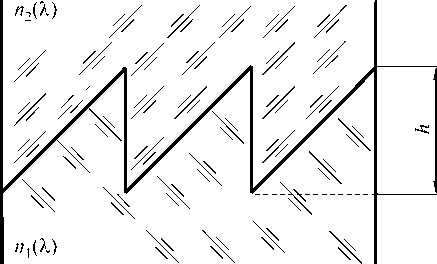
Рис. 1. «Ахроматическая» двухслойная рельефно-фазовая микроструктура с бинарным (а) и пилообразным (б) профилем штриха

В данной статье предлагается методика выбора материалов двухслойной рельефно-фазовой микроструктуры, обеспечивающая в заданном спектральном диапазоне с достаточно высокой точностью выполнение условия (2), а, следовательно, и выравнивание ДЭ в этом спектральном диапазоне.

Методика выбора оптических материалов

Реальный оптический материал (стекло, пластик или поликристалл) заменяется моделью, у которой показатель преломления в заданном спектральном диапазоне линейно зависит от длины волны используемого излучения

N ( λ ) = N + B ( λ-λ ),                        (3)

где N - показатель преломления модели на опорной длине волны X близкой к середине заданного спектрального диапазона. Отметим, что в формуле (3) и ниже показатель преломления модели и коэффициенты, входящие в него, в отличие от соответствующих величин, относящихся к реальным материалам, обозначены прописными буквами.

Замена конкретного материала моделью осуществляется путем линеаризации показателя преломления в заданном спектральном диапазоне, например, методом наименьших квадратов. В этом случае величины N и B определяются по формулам [5]

N =

JJ     J J    JJ

T X 22 T n +l j x- T x, | E x _yn -x T x _y z n i = 1 j = 1         k j = 1 ) j = 1               j = 1 j = 1

(

JЕУ-ТМ

, (4)

B =

J

J ТЛп,

JJ

- T X j T n j j = 1       j = 1

2 ^,

_ J

J T Xj-1T Xj

где J - количество отсчетов внутри заданного спек-

трального диапазона; n _j - показатель преломления реального оптического материала на длине волны X j .

Требование (2) при линеаризации показателей преломления в соответствии с выражением (3) обуславливает связь коэффициентов N и B моделей двух выбранных материалов, описываемую нижеследующим уравнением:

должна неуклонно возрастать, то материалы двух слоев должны иметь разную величину дисперсии и материал с меньшей дисперсией должен иметь больший показатель преломления. В случае стекол это реализуется парой, включающей крон (малая дисперсия) и флинт (большая дисперсия), причем показатель преломления крона должен превышать показатель преломления флинта.

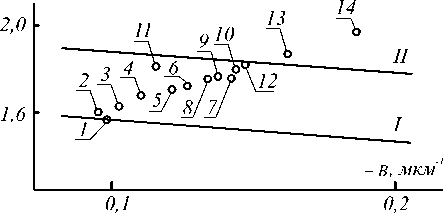
На рис. 3 в координатах N и B представлено семейство точек, соответствующих моделям 14 реально существующих флинтов, выбранных из отечественного и ряда иностранных каталогов стекла. Линеаризация показателей преломления этих стекол выполнена в интервале длин волн, охватывающем видимый и ближний ИК диапазоны ( X min = 0,4 мкм и X _max = 0,9 мкм), а в качестве опорной, принята длина волны излучения He-Ne лазера ( X= 0,6328 мкм). Параллельные прямые I и II на рис. 3 – зависимости

N 2 ( в 2 ) = N 1 + ( в 2 - B 1 ) X , (7) относящиеся ко второму слою, в случае если первый слой выполняется из моделей, полученных путем линеаризации в том же самом спектральном диапазоне показателей преломления кронов двух марок: BACED4 (каталог HOYA) и E65-40 (каталог OLD_CORN). Подчеркнем, что каждая из этих прямых является геометрическим местом точек, образующих семейство моделей флинтов, которые в паре с моделью соответствующего крона (в данном случае с BACED4 или E65-40) обеспечат строгое постоянство ДЭ.

( N 1 - N 2 ) + ( B ₂ - B 1 ) X = 0.

Здесь индексы 1 и 2 относятся к материалам первого и второго слоев микроструктуры, соответственно. Одновременное же выполнение условий (3) и (6) приводит к тому, что прямые зависимостей N 1 ( X ) и N ₂ ( X ) должны пересекаться в точке X = 0 , как показано на рис. 2.

N

MX)

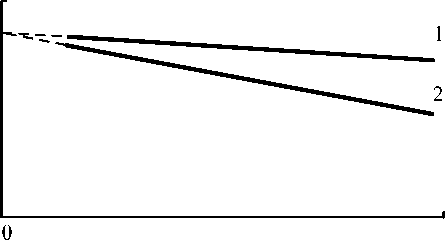
Рис. 2. Прямые зависимостей N 1 ( X ) (1) и N ₂( X ) (2), удовлетворяющих условиям (3) и (6)

При этом, поскольку, как следует из (2), с ростом длины волны разность показателей преломления

Рис. 3. Семейства точек, удовлетворяющих уравнению (7) (прямые I, II) и точек, соответствующих моделям флинтов (1-14):

• 1-    FF5 (каталог HOYA); 2- F2 (каталог SCHOTT);

• 3-    E-FD2 (каталог HOYA); 4- ТФ8 (каталог ГОСТ);

• 5-    FD1 (каталог HOYA); 6- FD10 (каталог OLD HOYA);

• 7-    FF8 (каталог HOYA); 8- SFL4 (каталог SCHOTT);

• 9-    FD14 (каталог HOYA); 10- FD110 (каталог HOYA);

11- LASF36A (каталог SCHOTT); 12- FD6 (каталог HOYA); 13- FDS90 (каталог HOYA);

14- SF58 (каталог SCHOTT)

Прямая I проходит через точку семейства, соответствующую модели флинта FF5, а к прямой II максимально близка точка, соответствующая модели флинта FD6 (оба стекла из каталога HOYA). Построив прямые N ₂( B ₂), соответствующие моделям всего ряда доступных для использования кронов, и

идентифицировав ближайшие к каждой из прямой точки семейства моделей реально существующих флинтов, найдем все «крон-флинтовые» пары, способные обеспечить с той или иной точностью постоянство ДЭ в заданном спектральном диапазоне. Сама же точность будет зависеть от двух факторов: во-первых, от того, насколько точка, соответствующая модели выбранного флинта, близка к прямой N ₂( B ₂) и, во-вторых, от достижимой точности линеаризации в заданном спектральном диапазоне показателей преломления выбранных крона и флинта.

Формулу для вычисления ДЭ рельефно-фазовой микроструктуры со ступенчатым профилем штриха (рис. 4), выполненной из стекла двух выбранных марок, можно получить, взяв за основу полученное в скалярном приближении выражение, приведенное, например, в [6]:

высота микрорельефа, обеспечивающая на длине волны X ₀, максимальную ДЭ, равна

h _

Р ⁽ n 01 ^- n 02) ’

где p _ 2 в случае бинарного и p _ 1 в случае пилообразного рельефа.

В случае однослойной структуры, выполненной из материала с показателем преломления n ₀ и расположенной в воздухе, высота микрорельефа, обеспечивающая на длине волны X ₀ максимальную ДЭ, равна

h '_—^X— Р ⁽ n 0 ^{- 1)}

.

П m

m sin21 л — I sin

I k J

п m

• 2

sin2

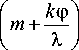
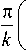
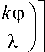
где

ф_ Xo (ni - n2 ) k (noi - n02 )

m - номер порядка дифракции; k - число ступеней в профиле штриха; X ₀ - длина волны, под которую рассчитывается микрорельеф с целью достижения на ней максимальной ДЭ; n и n 0 i ( i _ 1;2) - показатели преломления i -го слоя структуры на длинах волн X и X ₀ , соответственно; ф - приращение оптического пути за счет одной ступени профиля на длиневолны X .

Очевидно, что при использовании для изготовления рельефно-фазовой микроструктуры любых реально существующих оптических материалов h '< h .

Из полученного описанным выше способом набора «крон-флинтовых» пар наилучшую (с точки зрения решаемой задачи) можно выбрать, приняв одновременно во внимание высоту микрорельефа, необходимую для достижения на расчетной длине волны максимальной ДЭ, и степень отклонения ДЭ от максимального значения в заданном спектральном диапазоне. Последнюю можно оценить, в частности, по формуле

J

У (n max

j 1

^^^^^^в

j

J - 1

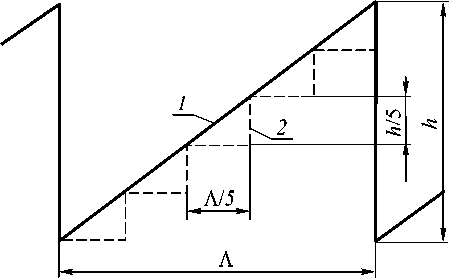
Рис. 4. Пилообразный профиль штриха микроструктуры (1) и его приближение ступенчатым профилем (2) при числе ступеней к _ 5

Напомним, что в приведенном на рис. 1 а случае бинарной микроструктуры, т.е. при к _ 2 , ДЭ в первом порядке дифракции достигает максимума при Аф _ п , в то время как в случае пилообразного или многоступенчатого профиля штриха ( к >  3 ) - при Аф _ 2 п . Поэтому, как это следует из выражения (1),

где J - количество отсчетов внутри спектрального диапазона; n max - максимальная ДЭ элемента, достигаемая на длине волны X ₀; n j - ДЭ элемента на длине волны X j .

Здесь необходимо заметить, что, варьируя X ₀ (т.е. изменяя высоту микрорельефа) можно минимизировать Ар и приблизить среднее значение ДЭ, вычисляемое как

1 ^J

{^р_ Е ,

J , _ 1

к максимально достижимому, т.е. к n _max-

В таблице приведены наиболее значимые параметры рельефно-фазовой микроструктуры с бинарным ( к _ 2) и десятиступенчатым ( к _ 10) профилем штриха, выполненной из пяти «крон-флинтовых» пар. Показатели преломления и коэффициенты дисперсии стекол приведены на желтой d - линии гелия ( X _d _ 0,58756 мкм). При этом с ростом номера пары в таблице показатели преломления кронов увеличиваются. Здесь напомним, что при к _ 2 максимально достижимая ДЭ в первом порядке дифракции n _max =0,41, а при к =10 максимальное значение ДЭ n _max =0,97.

№ п/п	Пары стекол	λ 0 , мкм	k	h , мкм	( η )	∆η
1	BACED4 ( n d=1,617652; ν d=55) FF5 ( n d=1,592703; ν d =35)	0,75	2	13,58	0,40	0,02
			10	27,17	0,94	0,05
2	BAF10 ( n d =1,670030; ν d =47) E-FD2 ( n d=1,647690; ν d =33)	0,70	2	14,40	0,40	0,01
			10	28,80	0,94	0,03
3*	CTK19 ( n d =1,744133; ν d =50) TФ8 ( n d =1,689493; ν d =31)	0,64	2	5,67	0,38	0,03
			10	11,35	0,90	0,08
4	E-LASF08 ( n d =1,88230; ν d=41) FD110 ( n d=1,784719; ν d =26)	0,62	2	3,12	0,38	0,03
			10	6,23	0,89	0,10
5	E65-40 ( n d =1,865000; ν d =40) FD6 ( n d=1,805184; ν d =25)	0,67	2	5,32	0,39	0,02
			10	10,65	0,93	0,05

* Данная пара предложена в [1].

Анализ распределений ДЭ двухслойных рельефно-фазовых микроструктур в пределах выбранного спектрального диапазона показал, что эти распределения для любой «крон-флинтовой» пары, полученные при различных k , подобны. Что же касается характера распределения, то он индивидуален для каждой «крон-флинтовой» пары, но отличия, как видно из рис. 5, не очень значительны.

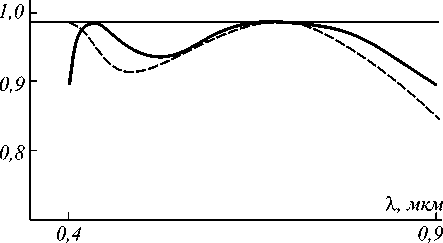
Рис. 5. Распределения ДЭ двухслойных десятиступенчатых рельефно-фазовых микроструктур, выполненных из двух «крон-флинтовых» пар: BACED4/FF5 (–––) и E65-40/FD6 (- - -); прямая параллельная оси абсцисс соответствуют максимально достижимому значению ДЭ для выбранного числа ступеней микроструктуры

Заключение

Как следует из представленной таблицы, платой за стремление обеспечить равномерность ДЭ по заданному спектральному диапазону и одновременно приблизить ее среднее значение к максимальному для выбранного числа ступеней в микрорельефе является значительная по сравнению с однослойной структурой высота рельефа. В то же время, используя пары стекол, включающие сверхтяжелые кроны, и оптимизируя для каждой пары значение расчетной длины волны λ0, можно при умеренной высоте микрорельефа получить как среднее значение ДЭ, так и ее равномерность, вполне приемлемыми для большинства применений.