Выбор места расположения внешних отвалов с учетом проветривания и минимизации выбросов пыли в рабочую зону карьера

Одной из важнейших проблем разработки месторождений полезных ископаемых открытым способом является обеспечение санитарных норм воздуха в карьере и санитарно-защитных зонах.

Открытые горные работы являются объектом с повышенной антропогенной нагрузкой на окружающую среду. При нестабильных метеорологических условиях, особенно когда меняются параметры естественного воздушного потока (скорость, плотность, температура), внешние отвалы периодически становятся источником загрязнений не только окружающей среды, но и воздушной среды собственной рабочей зоны карьера. При недостаточной интенсивности проветривания горных выработок карьера в них скапливаются отравляющие человека газы, а при интенсивном проветривании происходит пылеобразование, что приводит к хроническим заболеваниям человека, да и двигатели внутреннего сгорания, которыми оснащено современное горно-транспортное оборудование, требуют для их обслуживания больше расходных материалов и времени на текущий и капитальный ремонты. [1]

В связи с тесной взаимосвязью естественной воздушной среды с микроклиматом в горных выработках карьера аэрология карьеров приобретает все большую взаимосвязь с технологией организации открытых горных работ. Примером этому является выбор места расположения внешних отвалов, их геометрических параметров, форм, технологии отвалообразования.

Движения воздуха в карьере формируется в основном за счет естественного ветрового потока с учетом температурных неоднородностей воздушных слоев в горных выработках. Приток свежего воздуха, вовлекаемый во внутреннюю атмосферу карьера, должен иметь не только благоприятную концентрацию газов, но и естественную скорость, которая прямо пропорционально влияет на расход вовлекаемого чистого воздуха.[2]

Основными препятствиями для проникновения ветрового потока в карьер являются, например, внешние отвалы, инженерные сооружения на поверхности, административно-бытовые здания. Размещение «препятствий» в границах карьера с учетом технологии горных работ и метеорологических условий можно применить с целью управления воздушным потоком путем выявления и использования циркуляционных зон. Для достижения поставленной цели нами были проведены исследования по выявлению закономерностей формирования циркуляционных зон при обтекании естественным воздушным потоком препятствия - внешнего отвала.

В основу исследований положена аэродинамика свободного ветрового пока, которая базируется на теоретических положениях механики жидкостей и газов и законе движения жидкости, который выражен уравнением Навье-Стокса. Расчет течений вязкого сжимаемого газа, на основе уравнения Навье-Стокса, сопряжен с некоторыми трудностями по сравнению с расчетами течений несжимаемой вязкой жидкости. В течениях сжимаемого газа существуют не только области пограничных слоев, но и области больших градиентов искомых функций, которые соответствуют ударным волнам и волнам разрежения в невязких течениях газа.

Для численного моделирования двумерных течений в области обтекания отвала применена прямоугольная пространственная расчетная сетка. Топология регулярных сеток однозначно определяется индексами точек сетки. Сетка задана совокупностью узлов М= М i g( X i ,Y i ,i = Х,...П) и была представлена системой квадратов с вершинами М 1 ,М 2 ,...М n . Для построения разностной схемы применен интегрально-интерполяционный метод (метод конечного объема). Для прямоугольных сеток выбран контрольный объем в виде прямоугольника, что позволяет построить разностные аппроксимации. Разностная аппроксимация уравнений строится на основе приближенного интегрирования уравнений, записанных в потоковом виде по некоторому объему, который называется контрольным. Контрольный объем строится вокруг точек, в которых производится расчет газодинамических величин. Точность разностной схемы определяется способом выбора контрольного объема. Расчеты течений на неструктурированных сетках выбраны таким образом, что в круг, описанный около любого прямоугольника, не попадает ни один узел вершин указанного прямоугольника. [3]

Разностные аппроксимации строятся в потоковой форме непосредственно для векторов плотности потока массы j , вектора теплового потока q и тензора вязких напряжений П. Это соответствует записи уравнений газовой динамики в виде законов сохранения и делает алгоритм достаточно компактным и экономичным. Устойчивость разностного алгоритма обеспечивается присутствием искусственной диссипации, вид которой определяется квази-гидродинамическими добавками.

Для создания программного продукта, описывающего процесс обтекания ветровым потоком внешнего отвала с образованием циркуляционных зон, использовались следующие уравнения.

Система уравнений для решения задачи по обтеканию отвала методом конечных объемов в декартовой системе координат представлена в (1). Где первое уравнение системы является уравнением непрерывности (неразрывности). Его можно назвать законом сохранения массы. Второе и третье уравнения описывают движения сплошной среды. Последнее уравнение в этой системе описывает закон сохранения энергии.

jj

— + — + — = 0 txy

8 (Pu) , 8 (ju) । 5 (ju) + Рр = 6Пxx + 8Пxy t  x  yxxy

8(Pv) + dCjv) , 8(jv) + ср = 8Пxy + 8Пyy t  x  yyxy дE  д(jxH)  d(jyH) aqx  qqy   Q               а„

ПuПvПuПv xx      xy          xyyy t  x   y  xyxy где u, v, - проекции скорости потока на оси координат; р - плотность газа; j - плотность потока; p - давление; x, y - система координат; E -полная энергия единицы объема; H - полная удельная энтальпия.

_F__nи2 +v ² , Р E-^{p +} P

E                    , H         ,

2    Г-1       P p = pRT, jx = p>Uu-Wxx), jy = ^(v-Wy), где

W x

T

P

a (pu 2)  d( puv)  pp x  yx

_w _T a ⁽ pv ²)   ⁽(puv )  S p

Wy

x

Компоненты тензора вязких напряжений П представлены с помощью следующих выражений:

u 2

u2    u   v          u      u   p        p    p      uv

Пxx  2                    u u      v            u vp x3    x   y          x      y   x        x    y      xy

u

x

uv    u  up

П        uu   v xy      x y           x      y x

uv

uv

up

yx

xy

uv

xy

uv    v  vp

П        uu  v yx      x y           x      y y

xy

v 2

uv

v2    u   v           v      vp

Пyy  2                    v uv y3    x   y          x      yy

uv

uvp x y   xy

Компоненты вектора теплового потока имеют вид

T qx            u

x

T qy            v

y

3 ( up

3 Л vp pu        pv

1 x           1 y            x            y

x

3 г vp pu        pv

1 x           1 y            x            y

3 ( up

x

Коэффициент динамической вязкости // определяется линейным подобием относительно величины температуры воздушного потока.

Коэффициент теплопроводности % и релаксационный параметр т определяются в зависимости от коэффициента динамической вязкости.

R 1

У =------- И Т — ---

,

(   1)Pr        pSc где Pr - число Панделя; Sc - число Шмидта. [4]

Система уравнений (1) дополняется законом сохранения момента импульса:

x U divj x U x F tx

t

x Pe ^j

,

где x - координатная составляющая, P j - портер тензор P , e - базис

(в условных координатах сетки e 1 , e 2 ). [4]

Система уравнений (1) дополняется Вторым законом термодинамики:

( s ) t

div ( js )   div

q

T

X

Для моделирования обтекания воздушным приведенным уравнениям (системе уравнений)

потоком отвала по вводятся начальные

граничные условия.

Начальные граничные условия:

плотность входящего воздух будем считать постоянной и равной нормальному состоянию р = а_тмм ;

• •    естественный воздушный поток движется в одном направлении и пренебрегая подъемными силами, в связи со втором порядком малости, принимаем скорость потока: и = и вет , v = 0;

• •    считаем, что статическое давление является постоянным и равно 1 атмосфере р = Р атм .

Конечные граничные условия будут выражаться в более мягкую up форму: — = 0, — = 0, v = 0, — = 0.

xy           x

При этом граничные условия дополнены условиями не протеканием и не прилипанием воздуха к поверхности земли и отвала: U n uU_t =0, где U n , U_t - нормальная и тангенциальная составляющая скорости. [5]

Постановка граничных условий определяется конкретной решаемой задачей.

Решая систему уравнений (1) с добавлением формул (2) и (3), с учетом граничных условий, получаем следующие схемы (рис. 1) распределения динамического давления, плотности и скорости вдоль основной оси протекания ветрового потока.

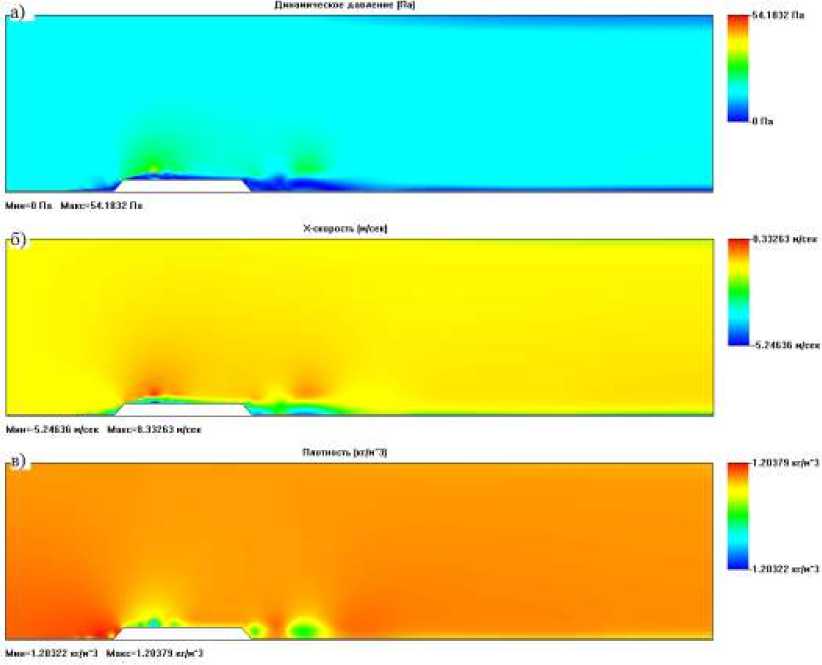
Рис. 1. Схема распределения динамического давления (а), плотности воздуха (б) и горизонтальных скоростей (в) при обтекании ветровым потоком одноярусного отвала.

Из схемы на рис. 1 следует, что при обтекании ветровым потоком отвала наблюдаются три циркуляционные зоны.

С наветренной стороны уступа отвала образуется отрыв потока, обращенный навстречу основному потоку, обусловленный положительным градиентом давления около поверхности перед уступом. Между точкой отрыва и точкой присоединения имеется турбулентный слой смешения. Течение в слое смешения между разделяющей линией тока и внутренней границей слоя поворачивает обратно перед уступом. Так как оно в дальнейшем вновь попадает в слой смешения вдоль его границы, то между стенкой и границей существует область течения воздуха с малой скоростью, то есть застойная зона. С наветренной части в точке присоединения потока образуется косой скачок уплотнения потока воздуха, обусловленный взаимодействием турбулентного слоя смешения, который направлен вдоль нулевой линии тока, с вязкой областью свободного потока. В ходе взаимодействия потоков образуется зона с отрицательным градиентом давления, который разворачивает движение воздушного потока в обратном направлении.

С подветренной стороны отвала поток отрывается у угловой точки (точка верхней бровки отвала) и присоединяется в точке вниз по течению, замыкая отрывную зону малых скоростей, где давление по существу постоянно и равно донному давлению за уступом. Внешний невязкий поток отделяется от вязкой области свободным слоем смешения, начало которого лежит в пограничном слое перед точкой отрыва. Кроме того течение в слое смешения аппроксимируется течением смешения при постоянном давлении турбулентного потока с покоящимся газом. Оторвавшийся слой смешения присоединяется в области больших положительных градиентов давления. Резкое возрастание давления разворачивает часть воздушного слоя смешения и этот слой в воздушном потоке течет в обратном направлении в застойную зону. Если сравнить воздушный поток с жидкостью, то жидкость, имеющая более высокую скорость, вытекает из донной области и продолжает движение вниз по потоку. [6]

Из описания циркуляционных зон следует, что перед началом циркуляционной зоны образуется характерное изменение давления и плотности воздуха, возникает начальная точка нулевой линии тока. В точки присоединения начинается восстановление всех параметров и оканчивается нулевая линия тока. Таким образом граничным условием для определение начала и конца циркуляционной зоны считается начальная и конечная нулевой линии тока. Граничные условия можно записать в следующей форме:

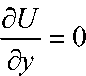
Для получения длины циркуляционной зоны построены графики зависимостей скорости и плотности в приземленных точках, которые находятся в пограничном слое (рис. 2). Из графиков определены длины циркуляционных зон, плотность ветрового потока и его горизонтальные скорости.

а)

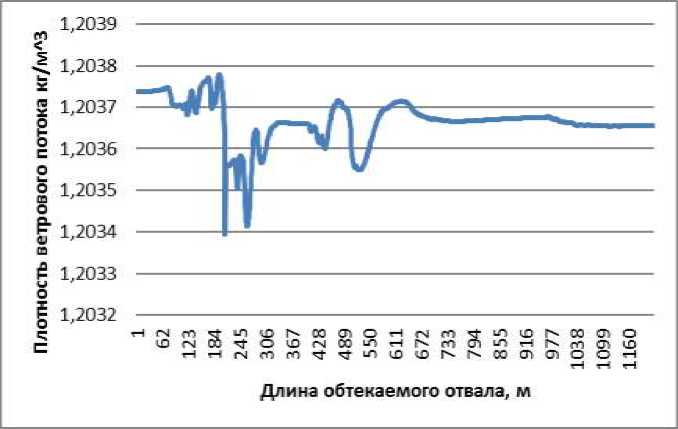
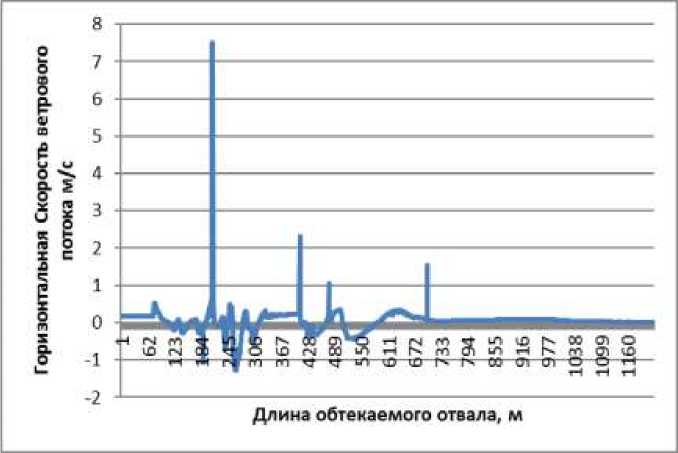
Рис. 2. График изменения ветрового потока при обтекании им отвала вскрышных пород: а - плотности воздуха, б - горизонтальных скоростей.

По результатам моделирования было получено следующее положение для расчета параметров второй и третей циркуляционной зоны: при малых числах Рейнольдса основными параметрами, влияющие на длину циркуляционной зоны, являются геометрические параметры отвалов (высота отвала, результирующий угол откоса отвала и ширина отвала поверху. [7]

Для уточнения зависимостей были рассмотрены графические модели четырех видов (рис. 3).

Рис. 3. Модели для расчета зависимости циркуляционных зон от геометрических параметров отвала: а – модель с изменяющейся высотой отвала; б - модель с изменяющимся наветренным углом отвала; в - модель с изменяющейся длинной отвала; д - модель с изменяющимся подветренным углом отвала.

На основании моделирования с использованием вариантов моделей (см. рис. 3) были установлены закономерности влияния циркуляционной зоны от высоты отвала, со стороны наветренного и подветренного угла, а также была выявлены возможные сочетания второй и третей циркуляционных зон при достаточно малой длине отвала. Графики зависимостей длины циркуляционных зон от технологических параметров отвала изображены на рис. 4.

На основе полученных из графиков зависимостей получены функции длины циркуляционной зоны от технологических параметров отвала.

l 11 H ^0.5 sin a

l ( ^l   l ) sin a

2H l 1   8H sin p l 2   5H1.15sinP где H - высота отвала, l - длина отвала, α – угол откоса отвала с наветренной стороны, β – угол откоса с подветренной стороны.

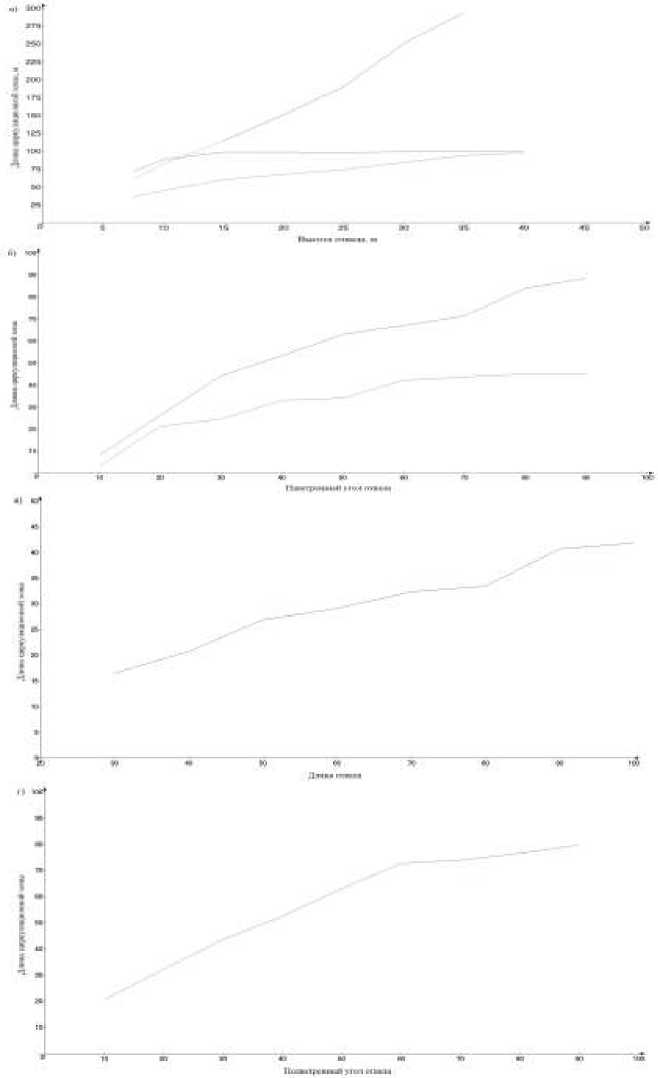
Рис. 4. Графики зависимости длины циркуляционной зоны от технологических параметров отвала: а – зависимость от высотой отвала; б - зависимость от наветренного угла откоса отвала; в - зависимость от длины отвала; д - зависимость от подветренного угла откоса отвала (зеленый график - первая циркуляционная зона, красный график - вторая циркуляционная зона, коричневый график - третья циркуляционная зона без взаимодействия со второй зоной, синий график - третья циркуляционная зона с взаимодействием второй зоной)

Основные выводы по результатам численного моделирования выбора места расположения внешних отвалов с учетом проветривания карьера и минимизации выбросов пыли в его рабочую зону:

• •    установлено, что минимальное расстояние от борта карьера до отвала должно быть не менее длины циркуляционной зоны с подветренной стороны для прохождения свежего воздуха в карьер с минимальным содержанием пыли;

• •    выявлена возможность управлять долями сочетаний второй и третей циркуляционных зон и даже объединять их в одну циркуляционную зону;

• •    установлены зависимости длины циркуляционной зоны от технологических параметров отвала.

840 с.

ветровой поток, циркуляционная зона, обтекание, отвал, скорость, плотность, динамическое давление wind stream, circulating zone, flow, dump, speed, density, dynamic pressure