Выбор модели для оценки профильных потерь в лопаточном венце с помощью методов математической статистики

проектного расчета, тем ближе проектная геометрия окажется к наилучшей для проектируемого изделия, и тем меньшее число обращений к дорогой в вычислительном плане CFD модели потребуется. В конечном итоге это приведет к сокращению времени получения финального варианта турбины и уменьшению необходимых для этого средств.

Ключевым вопросом повышения качества проектирования турбин является достоверное предсказание потерь энергии в ее проточной части. На сегодняшний день известно более десятка комплексных моделей, позволяющих рассчитать потери в осевых турбинах и еще несколько десятков уравнений, позволяющих рассчитать различные компоненты потерь [2, 3, 5, 6]. Эти модели потерь и уравнения были получены в течение последних 70 лет разными исследователями в разных странах. Авторы статьи поставили себе цель выяснить, какая из известных моделей точнее всего позволяет определить значение профильных потерь и характер их изменения под действие различных геометрических и режимных факторов. В дальнейшем планируется провести подобные исследования для других видов потерь, и найти наилучшую комплексную модель потерь.

Краткие данные о выбранных моделях потерь приводятся ниже.

С помощью упомянутых выше моделей потерь были рассчитаны значения профильных потерь в более, чем 170 решетках осевых турбин, геометрические и режимные параметры которых были взяты из источника [1]. Данный источник представляет собой справочник, содержащий данные экспериментальных продувок незакрученных по высоте решеток турбин, полученных на различных моторо- строительных предприятиях бывшего СССР. Данная информация была собрана и обобщена в ЦИАМ. Пример, информации о решетке и данных ее экспериментального исследования приведен на рис. 1. Диапазоны варьирования основных параметров рассмотренных турбинных решеток представлены в табл. 1. Рассматриваемый массив решеток отражает все многообразие профилей лопаток осевых турбин, используемых в авиационном ГТД.

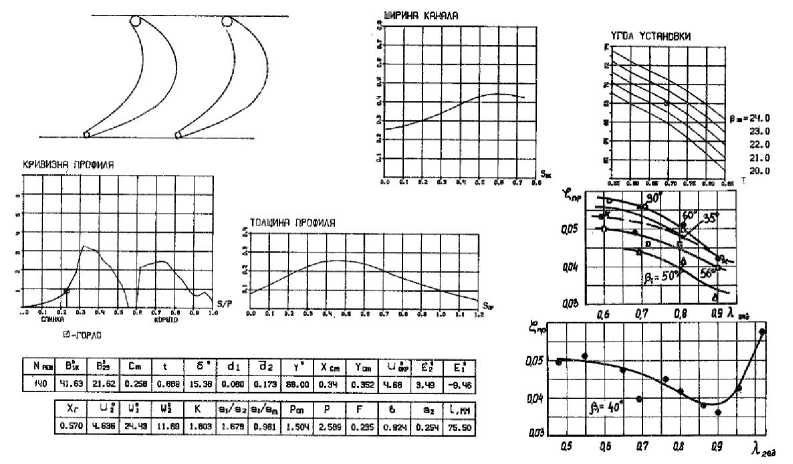
Рис. 1. Пример информации о решетке турбины и данные ее экспериментального исследования в источнике [4]

Таблица 1. Диапазоны варьирования основных параметров рассмотренных турбинных решеток

Название	Обозначение	Минимальное значение	Максимальное значение
приведенная скорость	■^-w2s	0,35	1,5
лопаточный угол на входе	ft,град	29	105
лопаточный угол на выходе	ft,град	7	44
угол поворота потока	Д / , град	61	137
относительная толщина лопатки	Г _ Ст! ^ т =    / b	0,08	0,36
относительное положение максимальной толщины	X с	0,09	0,47
угол отгиба профиля	8, град	-6	33
относительный шаг	t/b	0,505	1,05
относительная величина горла	аг /b	0,106	0,745
относительная толщина выходной кромки	2- Т2/ / а?	0,044	0,31
степень конфузорности канала	К	0,9	8,3

Примечание : величины углов потока в данной статье отсчитываются от фронта решетки

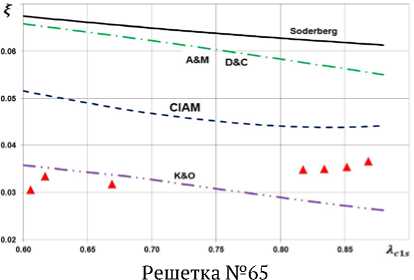
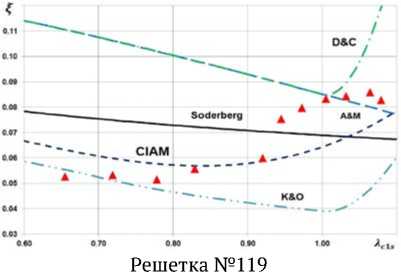
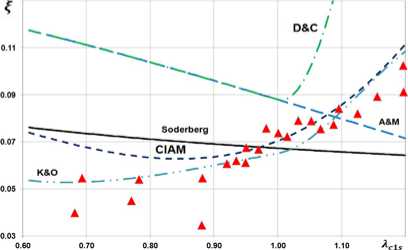
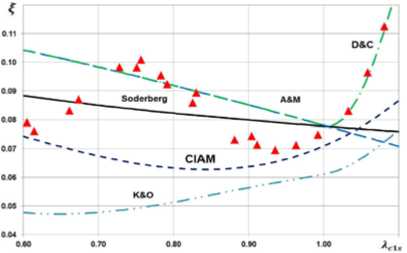
Среди экспериментальных данных для каждой рассмотренной решетки имеется зависимость значения коэффициента профильных потерь ξ от изоэнтропической скорости на выходе из решетки Aw2s. Подобные зависимости были получены для всех 170 решеток с помощью описанных выше моделей потерь и сопоставлены с экспериментальными данными. Результаты сопоставления для решеток №42, 65, 119, 135, 156, 174, выбранных случайным образом, показаны на рис. 2. Названные номера решеток соответствуют номерам в источнике [1]. Как видно из сравнения графиков на рис. 2, полученные данные не позволяют однозначно сказать, какая из моделей потерь является наилучшей. Любая из использованных моделей может для одной решетки давать практически полное совпадение, а для другой решетки показывать значение потерь, отличающееся от реального в 2 и более раза. Следует отметить, что чаще всего совпадение расчетных и экспериментальных данных наблюдается в около- звуковом диапазоне. При больших сверхзвуковых скоростях совпадения случаются существенно реже. В частности, модели Соделберга и Анлея и Метти-сона для сверхзвуковых скоростей потока в решетке принципиально неверно описывают тенденцию изменения потерь с ростом скорости течения. В дозвуковом диапазоне модели Анлея и Меттисона и Данхема и Кейма показывают идентичные результаты.

Для того, чтобы решить возникшую проблему и однозначно сказать, какая из моделей профильных потерь показывает лучшие результаты, был предложен следующий алгоритм. На первом этапе для каждой решетки массив экспериментальных данных был описан с помощью одного или нескольких регрессионных уравнений. Регрессионные уравнения представляли собой полиномы 3-6 степени вида fэксп = f(Xc1s). С помощью полученных регрессионных уравнений для каждой решетки были вычислены ожидаемые в эксперименте значения профильных потерь fэксп при значениях изоэнтропической приведенной скорости Xw2s от 0,6 до 1,2 с шагом 0,05. Аналогичным образом можно оценить ожидаемое значение профильных потерь при любом значении приведенной скорости Xw2s.

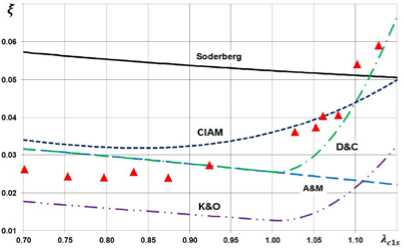
Решетка №42

Решетка №156

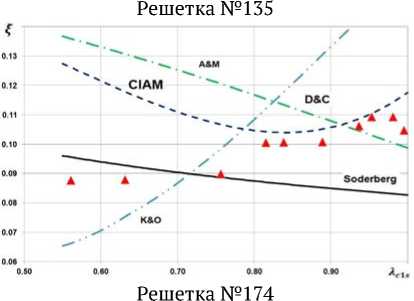
Рис. 2. Сопоставление результатов расчета профильных потерь с помощью разных моделей с данными эксперимента

Значения профильных потерь f _расч для тех же значений A _w2s были также рассчитаны для всех решеток с помощью выбранных моделей потерь. Затем для каждого вычисленного значения потерь было найдено его отклонение от ожидаемого экспериментального значения:

A f = (^{f pac4} —^f эксп ^ • 100%.

S расч

Таким образом, для каждой рассматриваемой модели потерь и для каждого рассмотренного значения приведенной скорости A _w2s было получено множество отклонений расчетных значений от экспериментальных данных A f . Каждое значение отклонения в каждом множестве соответствовало одной из рассмотренных решеток профилей (рис. 3-7).

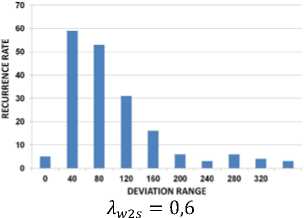
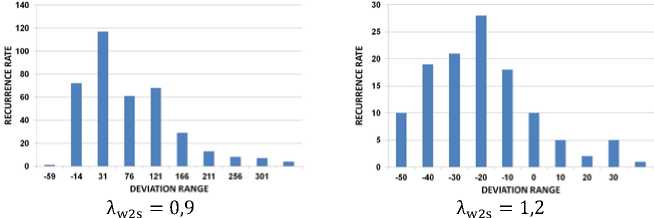
ис. 3. Гистограммы распределения значений отклонения для модели потерь Соделберга при разных значениях приведенных изоэнтропических скоростей потока

RECURRENCE RATE

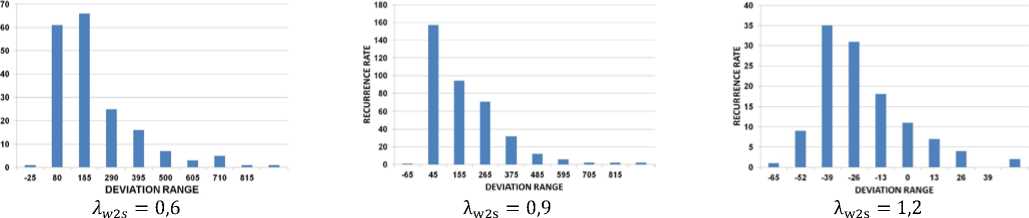
Рис. 4. Гистограммы распределения значений отклонения для модели потерь Анлия и Меттисона

при разных значениях приведенных изоэнтропических скоростей потока

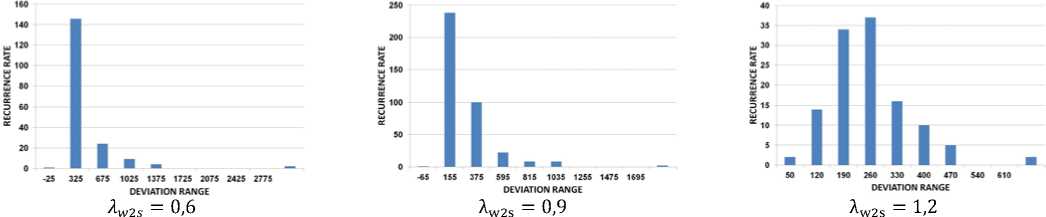
Рис. 5. Гистограммы распределения значений отклонения для модели потерь Данхема и Кейма

при разных значениях приведенных изоэнтропических скоростей потока

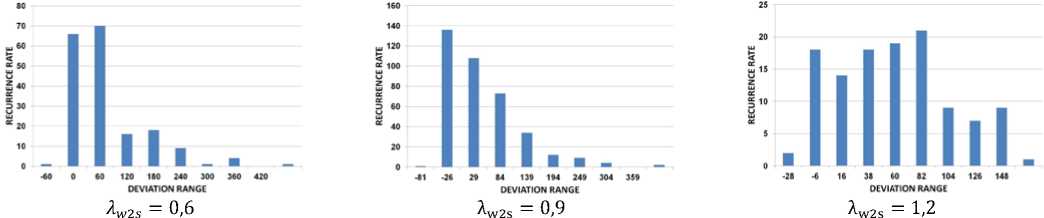
Рис. 6. Гистограммы распределения значений отклонения для модели потерь Какера и Окапу при разных значениях приведенных изоэнтропических скоростей потока

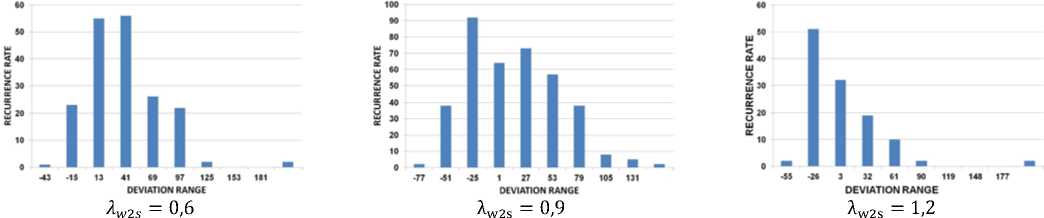
Рис. 7. Гистограммы распределения значений отклонения для модели потерь ЦИАМ при разных значениях приведенных изоэнтропических скоростей потока

Статистический анализ полученных данных показал, что внутри каждого полученного множества значение A f подчиняется нормальному закону распределения. Это позволяет для каждой рассмотренной модели потерь, для каждого рассмотренного значения изоэнтропической приведенной скорости A _w2s указать наиболее вероятное значение (математическое ожидание) д _А^ отклонения данных расчета от эксперимента A f , среднеквадратичное отклонение о а ^ , а также величину отклонения от среднего значения с вероятностью 95%, и найти численные значения д _А^ и о _а ^ .

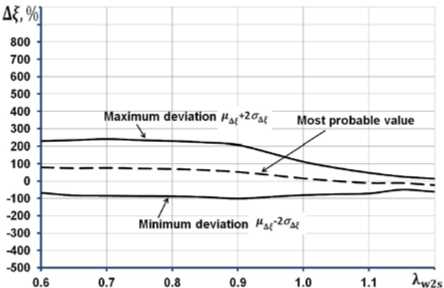
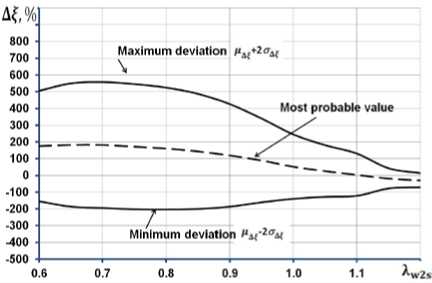
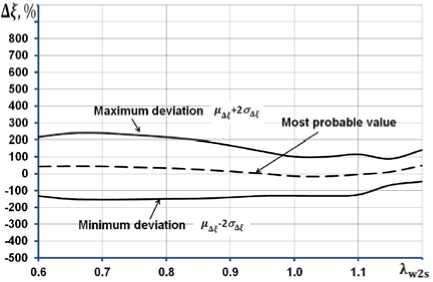
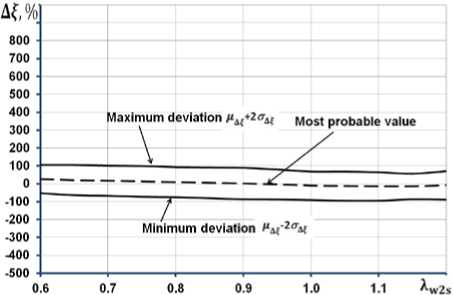
На рис. 8 показано, как изменяются наиболее вероятное значение отклонения расчетных данных от экспериментальных Af для разных значений изоэнтропической приведенной скорости Xw2s для всех рассмотренных моделей потерь. На том же рисунке обозначены найденные максимальные и минимальные возможные значения отклонений Af с вероятностью 95%, т.е. с указанной вероятностью отклонение вычисленного значения потерь от действительного значения на графиках рис. 3 будет лежать между кривыми, соответствующими максимальному и минимальному отклонениям.

Анализ данных на рис. 8 позволяет сделать вывод о том, что все рассматриваемые модели профильных потерь показывают наилучшие результаты (наименьшее отклонение наиболее вероятного значения и значение среднеквадратичного отклонения) в диапазоне приведенных скоростей от 0,8 до 1,2. Все рассмотренные модели потерь с большой вероятностью завышают значения профильных потерь при дозвуковых скоростях течения ( A_w2s менее 0,8). При этом отмечается большие, превышающие 200% среднеквадратические отклонения.

Soderberg mode

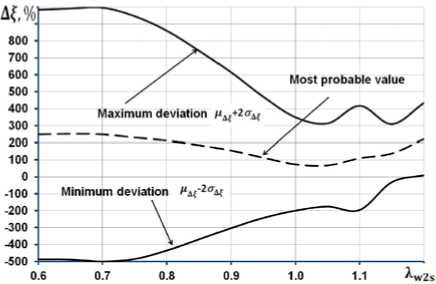
CIAM model

Рис. 8. Изменения наиболее вероятного значения отклонения расчетного значения профильных потерь от действительных значений и границ рассеивания с вероятностью 95% в зависимости от изоэнтропической приведенной скорости X _w2s для разных моделей потерь

По мере приближения скоростей к скорости звука уменьшается значение среднеквадратические отклонения, а значение наиболее вероятного значения уменьшается и для ряда моделей (Sodelberg, A&M, CIAM) становится отрицательным, что говорит о занижении расчетной оценки потерь. Наихудшие результаты из рассмотренных моделей показывает модель Данхема и Кейма, показывающая как большое математическое ожидание ^, так и среднекватичное отклонение од^. Их средние арифметические значения по всему рассматриваемому диапазону составляют 173% и 237% соответственно. Наилучшие результаты показывают модели Какера и Окапу (средние арифметические значения во всем в рассматриваемом диапазоне цд? = 20%; од^ = 73%) и ЦИАМ (средние арифметические значения во всем в рассматриваемом диапазоне ц^ = 2%; од^ = 41%). В целом обе указанные модели показывают близкие друг к другу статистические результаты, особенно в трансзвуковой области, однако предпочтение следует все же отдать модели ЦИАМ, поскольку у нее наименьшее значение как математического ожидания, так и среднеквадратичного отклонения из всех моделей. Более того, это значение стабильно, и мало меняется с величиной скорости течения. Также при анализе рис. 9 обращают на себя внимание неплохие статистические результаты показанные моделью Со-делберга. Несмотря на солидный возраст и свою некоторую примитивность, данная модель показывает в среднем следующие результаты (средние арифметические значения во всем в рассматриваемом диапазоне цд^ = 38%; од^ = 58%).

Представленная работа является первым этапом к поиску наилучшей модели потерь для осевой турбины и касается только профильных потерь. В дальнейшем аналогичным образом планируется проанализировать другие виды потерь, имеющие место в межлопаточном канале осевой турбины. В итоге планируется достоверно определить, какая модель является лучшей, либо разработать новую, превосходящую по точности существующие.