Выбор оптимального метода моделирования распространения импульсов в волоконных световодах

Волоконно-оптические линии передачи являются на сегодняшний момент основными каналами передачи информации. В волоконном световоде посредством модуляции лазерного излучения инфракрасного диапазона, (длина, волны излучения вблизи 1550 нм) работают наиболее широкие пропускные каналы информации. Промышленные волоконнооптические лазеры (длина волнві излучения вблизи 1064 нм) с КПД, приближающимся к 50% «от розетки», и не требующие значительного обслуживания, заняли лидирующее

«Московский физико-технический институт (государственный университет)», 2018

место в обработке материалов. Волоконно-оптические датчики по некоторым своим характеристикам сильно превосходят аналоги, спроектированные на базе предшествующих технологий.

Проектирование компонент и оптических систем, макетирование волоконно-оптических схем затрудняется без теоретического апробирования и сопровождения. В первом приближении линейной среды, когда показатель преломления считается постоянной величиной, возможно использовать аналитические оценки в расчётах. По мере приближения к границам возможностей технологий, эти оценки не дают достаточного представления о физических процессах. Появляется спрос на программные продукты, позволяющие учитывать большую часть физических процессов в случае распространения импульсов в волоконнооптических световодах. В большинстве случаев такие световоды имеют ступенчатый профиль показателя преломления [1]. Наиболее значимые эффекты, которые учитываются в расчётах: затухание, дисперсия, фазовая само- и кросс-модуляция, комбинационное рассеяние, нелинейные эффекты высших порядков.

Начиная с конца 90-х годов для системного решения описанных выше задач ведутся исследования и разрабатываются эффективные методы решения обобщённого управления распространения [1]:

ДА _ a    . х\ гпрп дпА dz      2     г n! dtn п=1

∞

A(z,t) [

R(t')IA(z, t — t')l 2 dt'

Многие проекты переросли в коммерческие продукты, когда, помимо самого решения уравнения, добавлены инструменты удобного задания начальных условий, визуализации физических процессов, подобно измерениям на измерительных приборах, таких как осциллограф, оптический анализатор спектра, анализатор ошибок, измеритель шумов и др. К таким продуктам относится программное обеспечение OptSim, VPItransmissionMaker, Optiwave Photonic. В большинстве случаев оно направлено на решение инженерных задач. Однако в применении к научному поиску такие программы не дают полного понимания механизма и критериев расчётов. Поэтому задача по эффективному решению уравнения (1) и анализа результатов актуальна.

В работах [3] 1984 г. и [4] 1999 г. показано преимущество фурье-метода расщепления по физическим процессам по сравнению с традиционными сеточными численными методами. Выбор модификаций и оптимизация этого метода позволяют существенно выиграть в скорости получения решения с заданной точностью [6-11]. Кроме того, в литературе встречаются работы, в которых предлагается использовать другие методы. Так, конкуретными по скорости являются вычисления методами на базе алгоритма Кренка-Николсона, сравнительный анализ и суть которого раскрываются в статьях [9], [11]. В другой работе [12] вместо гармонических функций предлагается использование вейвлетов.

2.    Постановка задачи и описание численного метода решения

Целью настоящего исследования является определение оптимального шага по переменной z для минимизации времени расчета и одновременного сохранения относительно высокой точности. Для описания распространения электромагнитных импульсов в волоконном световоде необходимо численно решить обобщенное уравнение распространения для медленно меняющейся амплитуды A(z,t) (1).

Произведем стандартную замену переменных:

^^Р ° ^Т 2 s ₌               ^A 3 . (2)

|A2| ,       ^оТо ,       6|А|Д)    ' '

и = А^, С = —, Т = t — Az, т = ^Т, N ² =

VP 0      L d ,         ¹¹ ,      Т о ,        L n

Перепишем уравнение (1) в новых переменных, оставив дисперсионные члены до 3 порядка включительно. В новых обозначениях получаем

= - ^U - ^sign^)    -      + i— ² (1+ is^- ) |U (4,т) [ R(f)\U (4,т - т ')|²dт '

04     2     2         от²    От³       \ от

Для расчетов будем пользоваться симметризованной схемой второго порядка точности по шагу. Для этого представим уравнение (3) в операторном виде:

=[^D+ ⁿ ( ^u )]^и

Здесь

и

^D = -^ ^- УтШ Д ^{- /!}Ф 2 2          от² от³

∞

U(4,т ) У R(t')|U (4,т - т')|²dт'

Функция отклика среды в нелинейном операторе может быть представлена в виде (1):

R(t = (1 - J rX^) + J r H r ,                           (7)

где первое слагаемое (с дельта-функцией) отвечает за мгновенный отклик, а второе - за рамановский (запаздывающий) отклик. Функция рамановского отклика определяется из эксперимента по спектру ВКР-усиления, здесь будем пользоваться моделью [2], в которой

-R = (т-2 + т—2)т1 exp(- —) exp( —), тг      ті где ті = 12,1 фс, т2 = 32 фс. Примем также Jr = 0,18 [1]. После подстановки (7) в (6) получаем

N(U ) = i(1 - J r )n ² u |² + і/rN²co nv(-R‘)-

-s(1 - J r —) Л [|U|²U] - sj r ) Л [Uconv(-R‘|U|²)].

Здесь com- (H _R ‘ |U|²) = ^f H r (т ')|U(т - т^r)|²dт '.

Решать уравнение (4) будем фурье-методом расщепления по физическим параметрам, то есть будем считать, что на каждом шаге дисперсия и нелинейность действуют независимо:

S + h

.                .               .Н                                                       Н                   .

^{U (}4 ^{+ H,t} ) = exp^D) ^exp⁽ J ^N((^,U )d( ^)exp⁽2D^)U(4,T ).             (8)

S

В этой схеме оператор нелинейности действует в середине шага, что позволяет сделать ошибку третьего порядка малости по Н [1].

Интеграл в (8) в некоторых случаях приблизим трапецией:

S + h

I N/(C,U)dC = |[7-(4 ) + N(4 + Н)].                         (9)

S

Так как в начале каждого шага мы не знаем, чему равно 1—(4 + Н), будем вычислять его по упрощенной схеме, в которой интеграл заменим просто на HN(4):

U '(4 + Н,Т ) = exp( -D) • exp(HN(4)) • exp( -D) • U(4,T ), 1—(4 + Н) = 1—(U').     (10)

3.    Определение оптимального метода расчета

Характерные длины, на которых проявляются нелинейные и дисперсионные эффекты, г 2

составляют L q = -g° и L n = z^- Логично выбирать шаг интегрирования много меньше каждой из этих длин. Можно, например, взять h = 0, 01 • min(Lp, L n ), однако по мере распространения импульса пиковая мощность импульса и его длительность могут существенно меняться. Так, в случае распространения солитона, например, третьего порядка, его пиковая мощность в разные моменты эволюции может различаться в 3 раза. Требуется менять шаг интегрирования по zb зависимости от текущей пиковой мощности. Данный метод известен и используется, например, в [6].

В ходе разработки программы расчета были опробованы различные схемы численного решения:

• 1)    Простая схема второго порядка точности по h с постоянным шагом (coarse; constant step):

U(е + h,T ) = exp(2 D) • exp(hNO • exp(2D) • U(e,T ),          (11)

h = co list.

• 2)    Улучшенная схема второго порядка точности по he постоянным шагом, описанная в (8), (9), (10) (precise; constant step):

U (£ + h,T ) = exp(2D) • exp(2[W(e) + W + h)]) • exp(2D) • U(e,T ),     (12)

W + h) = N(U ‘), hh

^{U (e + h,T} ) = ^exp⁽2^D) • ^exp^(hM^e)) • ^exp⁽2^D) • ^U(е,Т ), h = co list.

• 3)    Простая схема второго порядка точности по he переменным шагом (coarse; variable step):

h h

U(е + h,T) = exp(2D) • exp(h^v(e)) • exp(2D) •U(е,Т),            ид h =

(пиix | u (е)|)2.

• 4)    Улучшенная схема второго порядка точности по he переменным шагом (precise; variable step):

U(е + h,T) = exp(2D) • exp(2[W(e) + W + h)]) • exp(2D) • U(£,T),(14)

N(e + h) = N(U ‘), hh

U (e + h,T) = exp(2D) • exp(hMe)) • exp(2D) •U(e,T), h =

(in;ix|U(е) | )2 .

Были произведены расчеты по всем указанным схемам, а также по схеме, предложенной в [6], с целью определения оптимального по производительности метода. Для определения точности метода удобнее всего сравнивать численное решение с точным аналитическим. Так как уравнение распространения в общем виде (3) не имеет аналитических решений, для оценки точности методов будем решать уравнение в случае, когда a = 0. Проводя аналогию, его иногда называют обобщённым нелинейным уравнением Шредингера (ОНУШ):

= - l_Sign(/32) д^ + iN ²|U |²U.                         (15)

Аналитическое решение этого уравнения при начальном условии Uo = VP0 • ^seсһ(Т/Тз) и при таких P o и То, что 7P)Tq/|/32 | = N 2, является квадратом целого числа и солитоном порядка N. Оно периодично по z с периодом zg = 7 L d или, в безразмерных координатах, с периодом Eg = 7. В качестве функции ошибки будем использовать две метрики:

/ ||U₀|-|U (zg)H 2 dT ^err11-11 =       /|UoRT

т

и

СП-1.| = |max|Uo| - max|U (zg )||. (17)

Здесь Uq - комплексная амплитуда при z = 0. Как мы знаем из аналитического решения, она же - при z = zg. В качестве приемлемого у ровня ошибки выбираем егг||-|| = 10^-3 и ориентировочное время расчета приводим именно для такого уровня. В статьях также часто используется данное предельное значение. Графики приводятся вплоть до 10—4.

Будем рассматривать импульсы длительностью Т = 1 пс и центральной длиной волны Ао = 1550 нм, распространяющиеся в волокне с дисперсией групповых скоростей /З2 = -20 ^ и пара метром 7 = 26 _км1_В . Дисперсионная длина при таких параметрах составляет L d = 50 м, а период солитона примерно zg = 78, 5 м.

Разбиение по Т должно быть таково, чтобы выполнялось dT ^ T fwhm (z) V z Е [0, zg]. В наших тестах будем брать dT <  4 фс. Когда мы решаем уравнение (15), в таком мелком разбиении нет необходимости, однако при решении уравнения распространения (3) в общем виде необходимо, чтобы шаг по Т был меньше характерного времени изменения функции h _R ( t ).

4.    Результаты вычислений и их анализ

Начнем с метода (11), с самого простого. Рассчитаем точность метода в зависимости от шага интегрирования для солитонов различных порядков. Шаг в методе (11) постоянный, будем выбирать его в виде һ = е • ш in(Lp, Ln ), г де е ^ 1. Начнем с солитона первого порядка, для него L n = L d = 50 м.

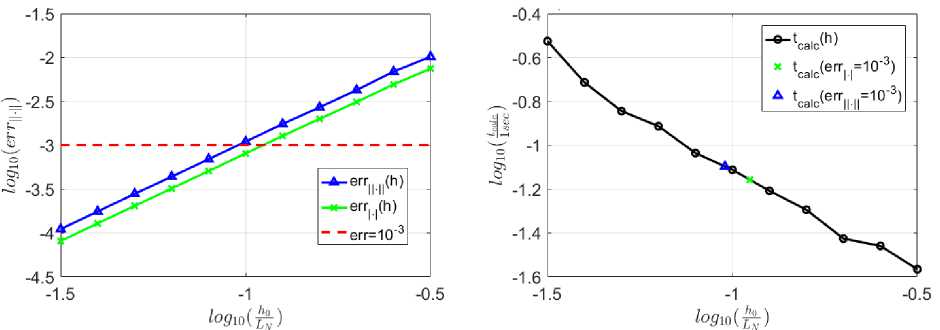
Рис. 1. Зависимость ошибки и времени вычисления от шага интегрирования по z при постоянном шаге для N = 1. Метод (11) (coarse; constant step). Время счёта 0,1 с

На графике слева в логарифмических координатах изображены ошибки вычисления (интегральные, после прохождения всех шагов по z) в зависимости от величины шага интегрирования. Пунктиром обозначен уровень ошибки 10-3. На графике справа в логарифмических координатах приведено время расчета с соответствующим шагом. Треугольником и крестиком обозначено время расчета с точностью 10-3 (на основе интерполяции по левому графику).

Как видно из рис. 1, уже при шаге ^о = 0,1 • min(Lp , L n ) достигается точность 10-3, при этом время расчета распространения на период солитона составляет всего ~ 0,1с. Из рисунка также видно, что метод имеет второй порядок точности по ^о, так как в логарифмических координатах функции ошибки линейно зависят от шага, а тангенс угла наклона прямой равен 2. Приведем также аналогичный рисунок для солитона пятого порядка.

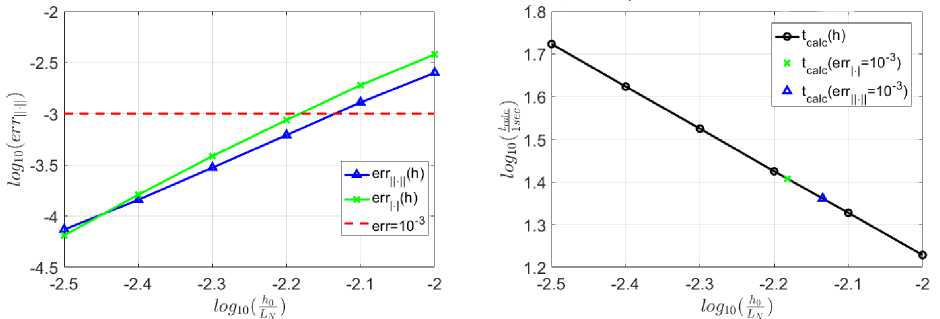
Рис. 2. Зависимость ошибки и времени вычисления от шага интегрирования по г при постоянном шаге для N = 5. Метод (11) (coarse; constant step). Время счёта 23 с

Здесь заданная точность достигается при шаге ^о ~ 0, 0073 • Ln, время расчета с заданной точностью уже около 23 секунд. Аналогичные расчеты были произведены для солитонов 1-10 порядков, время расчета с заданной точностью приведено на рис. 3.

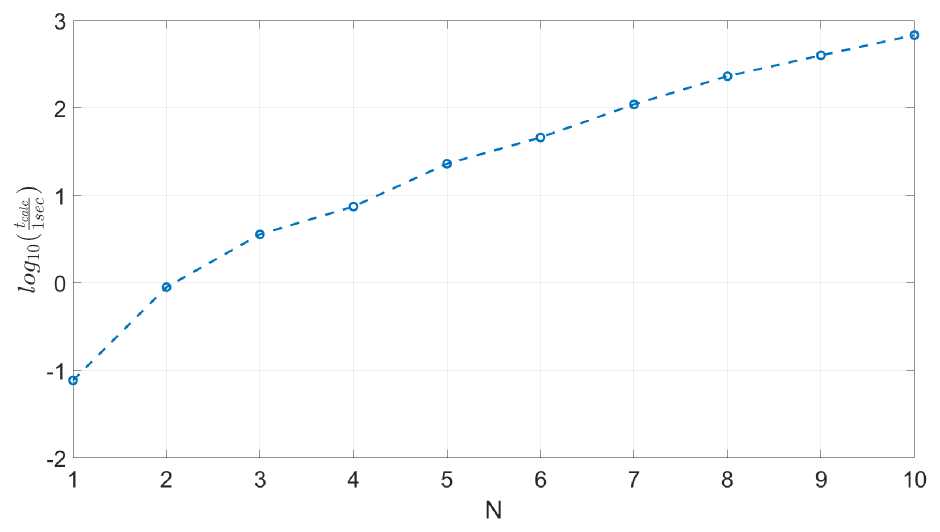
Рис. 3. Время расчета распространения солитонов различных порядков на расстояние zg ~ 78, 5 м с заданной точностью. Результаты метода. (11) (coarse; constant step)

Из рис. 3 видно, что время расчета, например, солитона 10 порядка составляет более 11 минут.

Метод (12) или precise; constant step, оказывается более медленным для солитонов порядка вплотв до 4, а начиная с 5 уже дает выигрыш во времени расчета с заданной точностью. На рис. 3 приведена точноств метода в зависимости от шага интегрирования при расчете распространения солитона 5 порядка.

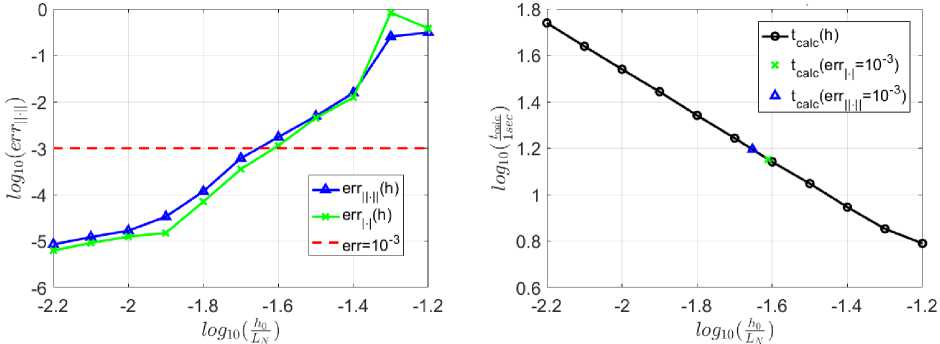
Рис. 4. Зависимость ошибки и времени вычисления от шага интегрирования по z при постоянном шаге для N = 5. Метод (12) (precise; constant step). Время счёта 15,7 с

Как видно из рис. 4, метод имеет более высокую точность по Һ, так как средний угол наклона кривых на левом графике составляет около 4, что соответствует методу 4 порядка точности. Однако для солитонов более высоких порядков средний наклон кривой уменьшается и составляет около 3. На рис. 5 приведена аналогичная зависимость для солитона 9 порядка.

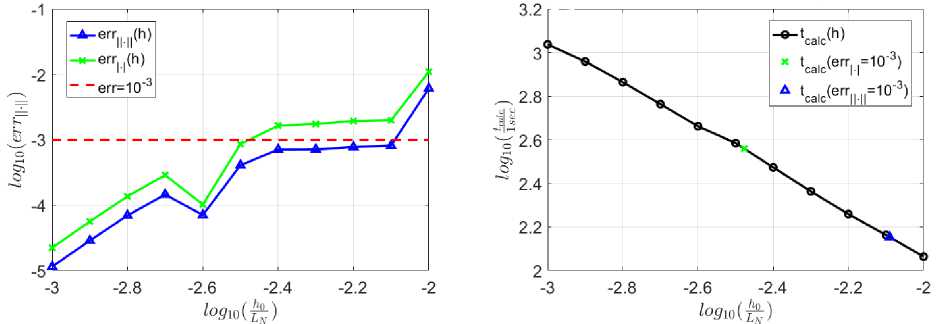
Рис. 5. Зависимость ошибки и времени вычисления от шага интегрирования по z при постоянном шаге для N = 9. Метод (12) (precise; constant step). Время счёта 142,3 с

На следующем рисунке приведем зависимость времени вычисления с точностью 10-3 для солитонов различных порядков.

Время расчета распространения солитона 10 порядка методом (12) с точностью 10-3 составляет 211 секунд, что более чем в 3 раза быстрее метода (11).

Метод (13) или coarse; variable step, дает очень хорошие результаты по производительности. Этим методом также было рассчитано распространение солитонов 1-10 порядков. Начиная с солитона второго порядка, он быстрее метода (11) и для солитонов всех порядков быстрее метода (12). Зависимость времени вычисления с точностью 10-3 по схеме (13) для солитонов различных порядков приведена на рис. 7.

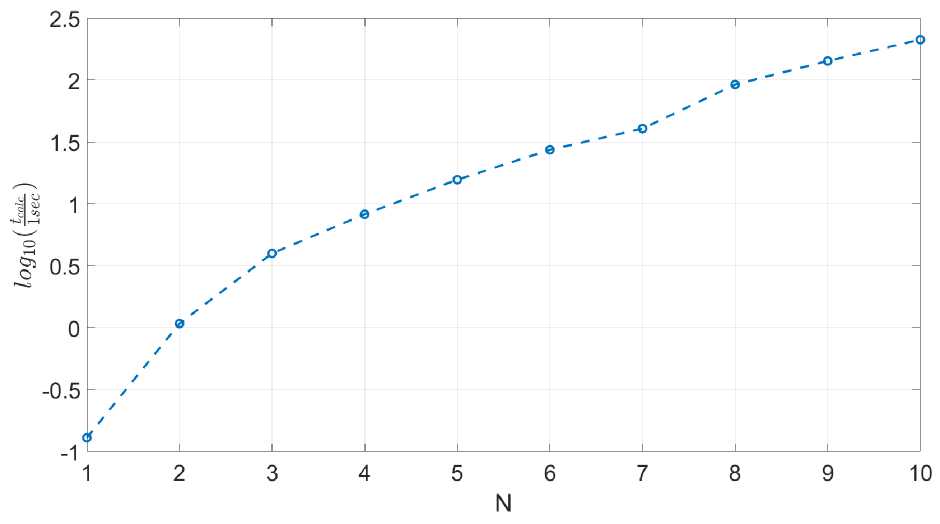
Рис. 6. Время расчета распространения солитонов различных порядков на расстояние zg ~ 78, 5 м с заданной точностью. Результаты метода. (12) (precise; constant step)

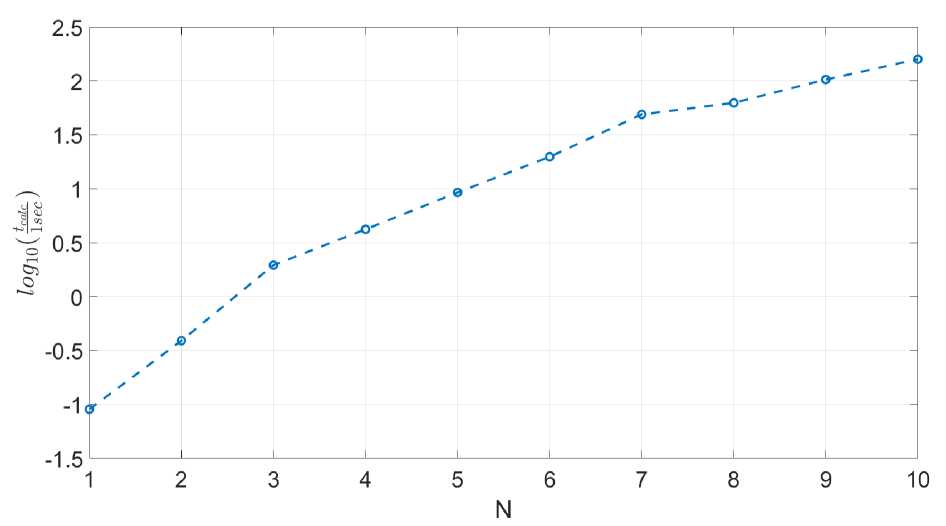
Рис. 7. Время расчета распространения солитонов различных порядков на расстояние zg ~ 78, 5 м с заданной точностью. Результаты метода. (13) (coarse; variable step)

Метод (14) или precise; variable step, является комбинацией методов (12) и (13). Можно было ожидать, что этот метод окажется наиболее эффективным.

Однако, как оказалось, это не так. Он проигрывает методам (12) и (13) и выигрывает лишь у метода (11). По крайней мере, при вычислении с точностью 10-3. На следующем рисунке приведена, производительность метода. (14) для солитонов различных порядков.

Вполне может оказаться, что этот метод эффективнее (вследствие теоретически более высокой точности) при расчете распространения более мощных импульсов. На практике практически не встречаются ситуации, когда, энергия импульса, в волоконном световоде соответствует энергии солитона таких высоких порядков (более 100 энергий фундаментального солитона).

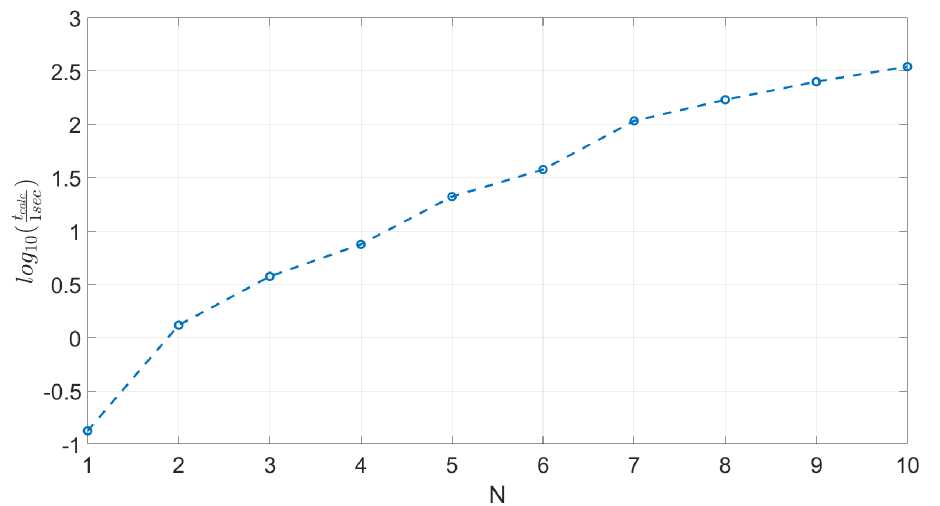
Рис. 8. Время расчета распространения солитонов различных порядков на расстояние zg ~ 78, 5 м с заданной точностью. Результаты метода. (14) (precise; variable step)

Приведем сравнительный график производительности всех четырех методов.

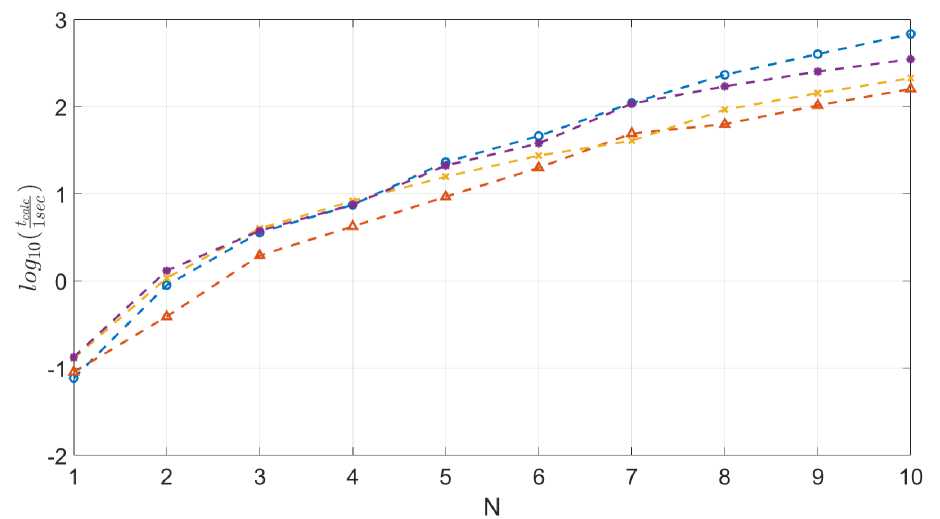
Рис. 9. Результаты сравнительного теста, всех четырех методов: о - метод (11) (coarse; constant step), △ - метод (12) (precise; constant step), x - метод (13) (coarse; variable step), • - метод (14) (precise; variable step)

Время расчета, с заданной точностью в упрощенной модели (4) и время в полной модели (12) существенно различаются, так как в полной модели каждый шаг содержит больше вычислений. Можно ожидать, что шаг интегрирования по z, при котором достигается заданная точность, будет тем же самым.

Расчет задачи распространения в среде с положительной дисперсией требует гораздо меньше времени для достижения заданной точности, так как амплитуда резко снижается, также снижается роль нелинейности, а именно расчет нелинейного оператора является преимущественным местом накопления ошибок. Таким образом, при расчете задачи в среде с положительной дисперсией можно пользоваться любыми методами, хотя предпочтительными являются методы (12) и (13).

Таким образом, показано, что оптимальный выбор метода вычисления позволяет в несколько раз уменьшить время вычислений, что дает возможность получить рабочий приемлемый инструмент для теоретических исследований.