Выбор оптимального плана использования системы лесомелиоративных машин

Введение . Необходимость разработки научно обоснованных рекомендаций по рациональному использованию систем лесомелиоративных машин в зависимости от конкретных природно-хозяйственных условий не вызывает сомнений. Проводимые в этом направлении исследования должны базироваться на оптимальном расчете сложной системы «объект лесозаготовок – лесная машина», чтобы обеспечить надежную, эффективную и универсальную методику, которая бы позволяла на основе системного подхода, математического моделирования и оптимизации еще на стадии планирования произвести оценку и прогнозирование основных технико-экономических параметров.

При рассмотрении задачи лесомелиорации априорно можно принять, что в существенной степени на величину осушенных площадей, которые можно будет перевести в лесопользование с целью получения товарной древесины, оказывает влияние принятая технология, базирующаяся на том или ином комплексе (системе) гидролесомелиоративных машин. Очевиден и следующий тезис о том, что максимальное вовлечение в активное лесопользование площадей можно обеспечить в том случае, если эффективность функционирования лесомелиоративных машин будет определяться величиной прибыли от реализации полученной товарной продукции при обязательном обеспечении экологических и производственных норм.

Цель исследований . Произвести расчет оптимального плана использования системы машин непосредственно на объекте гидролесомелиорации. При этом постановка задачи может заключаться в следующем. Имеется несколько видов специальных машин для строительства открытой осушительной сети, различных по технико-экономическим показателям, и несколько участков с различными природнопроизводственными условиями. Целевой функцией для оптимизации является общая прибыль, определяемая разницей ожидаемой прибыли от эксплуатации осушаемого участка и стоимости работ по его осушению.

Методика и результаты исследований. Неуклонно растущая производительность вычислительной техники предопределяет возможности по применению принципиально новых более точных методов анализа таких сложных систем, которые могут учитывать в своей работе огромные объемы входной информации. Например, в настоящее время быстрыми темпами растет рынок услуг по предоставлению картографической информации, получаемой с помощью обработки данных дистанционного зондирования земли (ДЗЗ). Исполь- зование таких данных в качестве экономически доступного и объективного источника информации позволяет полностью решить вопрос дешевого получения актуальной цифровой карты местности (ЦКМ).

Введенные в данный момент в эксплуатацию спутники позволяют получать исходные ортофотопланы сверхвысокого разрешения с плотностью до 0,5 м на пиксель. Например, космический аппарат (КА) WorldView-2 по информации сайта оператора обеспечивает пространственное разрешение в надире 46 см [1] . Причем, помимо ортофотопланов в видимом диапазоне волн, требуемых для построения базовых топографических слоев – лесных массивов, дорожной и гидрографической сетей, населенных пунктов и инженерных объектов, линий ЛЭП, трубопроводов и других, а также данных о высотной модели рельефа, такие спутники получают ДЗЗ и в мультиспектральном диапазоне волн. Их дальнейшая обработка позволяет получить множество тематических данных о природно-хозяйственных условиях интересующих участков.

Так, например, мультиспектральная съема обеспечивает данные в следующих диапазонах [3] : зона 0,52–0,60 мкм соответствует максимальному коэффициенту отражения зеленой (здоровой) растительности, зона 0,63–0,69 мкм содержит полосу поглощения хлорофила, что позволяет различать множество разновидностей растений. Зона 0,76–0,90 мкм особенно чувствительна к количеству вегетационной биомассы, что позволяет определить потенциальную урожайность почвы. Зона 1,55–1,75 мкм позволяет определить содержание воды в растительности и почве, а с помощью зоны 2,08–2,35 мкм можно выделить границы почв, а также степени увлажненности почв и растительности.

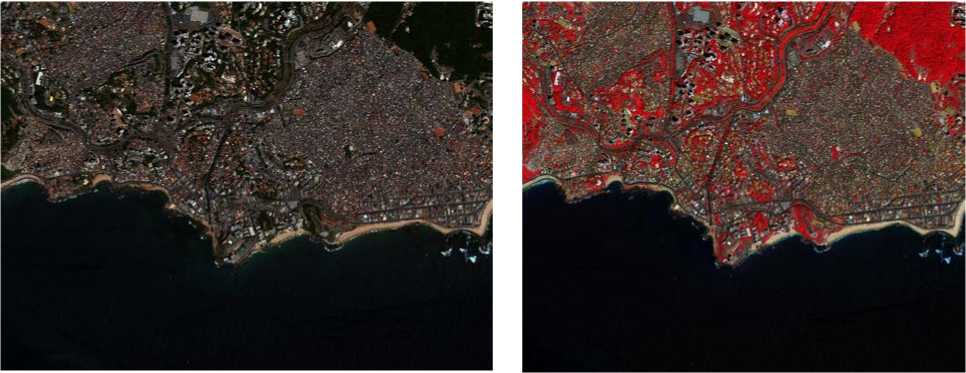
Рис. 1. Пример спутникового снимка в видимом диапазоне волн (слева) и спектральном (справа)

Так, на рис. 1 приведены два спутниковых снимка, снятых КА WorldView-2 [4] в видимом диапазоне, и с того же ракурса в спектральном диапазоне, на котором красному цвету соответствует диапазон волн 0,76–0,90 мкм, интенсивность которого показывает количество вегетационной массы.

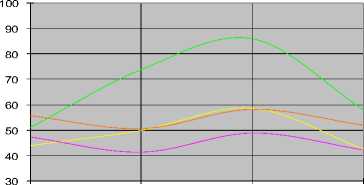
Ближний инфракрасный канал (Near Infrared Band - 720 nm)

МАЙ / MAY ИЮНЬ / JUNE     АВГУСТ      СЕНТЯБРЬ /

/AUGUST     SEPTEMBER

Лиственница (Larch)      Ель (Spruce)

Береза (Birch)             Сосна (Pine)

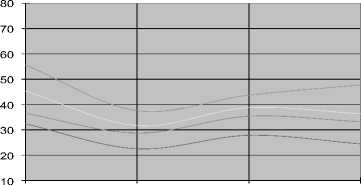
Средний инфракрасный канал (Medium Infrared Band - 1550 nm)

МАЙ / MAY ИЮНЬ / JUNE     АВГУСТ      СЕНТЯБРЬ /

/AUGUST     SEPTEMBER

Лиственница (Larch)      Ель (Spruce)

Береза (Birch)             Сосна (Pine)

Рис. 2. Динамика спектральных яркостей лесных пород в течение вегетационного сезона

На рисунке 2 [1] приведены графики динамики спектральных яркостей лесных пород в течение вегетационного сезона в ближнем и среднем инфракрасных диапазонах, по которым можно произвести дифференциацию породного состава. Применяя такие комбинированные данные, можно автоматически провести инвентаризацию лесного фонда [5] по таким параметрам, как:

• •    определение категорий (лиственные, хвойные) и породного состава лесов;

• •    подразделение лесов на категории по возрасту, степени спелости, запасу древесной массы, биологической продуктивности;

• •    определение высоты лесных массивов;

• •    изучение природных условий, способствующих или препятствующих активной лесохозяйственной деятельности (выявление плоских пониженных заболоченных участков, бессточных котловин, резких перегибов рельефа с применением цифровых моделей рельефа);

• •    изучение негативных процессов, воздействующих на лесные массивы (влияние вредителей и болезней, иссушение или переувлажнение лесов, приводящих к их деградации и гибели);

• •    оценка состояния лесных насаждений с хронической формой ослабления деревьев болезнями, промышленными выбросами, чрезмерной рекреационной нагрузкой и т.п.

Необходимость учитывать все эти данные при построении математической модели не вызывает сомнений. Определим математическую модель задачи оптимального плана использования машин на объекте лесомелиорации следующим образом. Будем считать, что модель объекта лесомелиорации задается с помощью ЦКМ, на которой на соответствующем тематическом слое определены участки осушения с обозначением планируемой схемой осушительной сети. Будем считать, что количество таких участков равно М. Используя описанные выше данные ЦКМ, можно автоматически вычислить для каждого такого участка следующие величины:

Q j – ожидаемая после осушения прибыль в рублях от эксплуатации j-го участка, полученная исходя из оценки запасов биомассы в насаждениях, j=1..М;

W j – объем работ по строительству каналов в метрах, необходимых для осушения j-го участка, вычисленная исходя из обозначенной схемы осушительной сети и определенного в ней объема работ, j = 1..М.

При построении математической модели мы не будем проводить декомпозицию функционирования системы лесомелиоративных машин, решая лишь задачу определения оптимального их числа, рассмотренную с точки зрения обеспечения согласованности их взаимодействия в рамках выделенной системы. Таким образом, будем считать, что у нас имеется N однотипных по виду работы машин, разных по своим характеристикам, определяемым как моделью машины, так и ее особенностями. Также рассмотрим последовательный период из D дней, выделенных для проведения осушительных работ.

Для упрощения введем естественное ограничение, что каждая машина за один день работает одну смену на одном участке, т.е. машина не может работать в один день на двух участках сразу или работать в несколько смен.

• В ведем еще 2 набора входных параметров:

w ijk и p ijk – это объем работ в метрах в день, которые можно выполнить, назначив i-ю машину на j-й участок в k-й день, и стоимость в рублях (i=1..N, j=1..M, k=1..D).

Определим план-график X через набор величин X jk e {0, 1} (i=1..N, j=1..M, k=1..D). Примем X jk =1, если i-я машина работала на j-м участке в k-й день, или x ijk =0 в противном случае.

Для любого определенного таким образом плана-графика X выполняются два следующих ограничения. Первое ограничение определяет невозможность назначения одной машины на два участка в один день. При этом мы оставляем возможность иметь простои:

M

X x*

J = 1

V i = 1.. N

< 1,               .

V k = 1.. D

Второе ограничение определяет необходимость проведения полного цикла работ по осушению j-го участка или полного отказа от его разработки:

W

V j = 1.. M .

ND

XX w k x k i = 1 k = 1

Введем величину T j следующим образом:

ND

T j =

EE ^wj X k

, V j = 1.. M .

i = 1 k = 1 ____________

W j

Отметим, что T j =1 в случае, если j-й участок принят к осушению, и T j =0 в противном случае. Используя данную величину, можно для каждого плана графика вычислить полную ожидаемую прибыль П(X) и планируемые затраты C(X):

M

П ( X ) = E QT

J = 1

MDN    .

C ( X ) = EEE p jk X jk j' = 1 k = 1 i = 1

Тогда задачу оптимизации совокупной прибыли R(D) можно поставить следующим образом:

R ( D ) = MAX [ П ( X ) - C ( X )] .

Вычисление совокупной прибыли R(D) для всех возможных D и дальнейший анализ этой величины позволяет определить оптимальный план работ и сроки. Отметим, что ввиду введения ограничения о возможности получения прибыли с участка только при выполнении полного цикла работ по его осушению функция R(D) будет ярко выраженной негладкой функцией, т.е., например, незначительное увеличение сроков работ может привести к значительному изменению совокупной прибыли. Поэтому финальный выбор оптимального плана лучше проводить вручную в зависимости от имеющихся совокупных факторов. Рассмотрим математическую постановку этой задачи. Очевидно, что образуя свертку декартова множество количества машин и количества дней S=NxD в линейное заменой индекса (i,k) на s = (i – 1) * D + k (s = 1..S), и обозначив через wsl      Vj = 1.. M

Q sj

• ¹    WX~^PsJ, V s = 1.. S ’

мы можем свести задачу оптимизации совокупной прибыли к следующей задаче:

MAX IE E Csjxsj, xsj e {0,1}, если s =1 j=1

E x_sj < 1, V s = 1.. S               .

j = 1

W

E wsjxsj=\ Л V j = 1..M s =1                I 0

Физический смысл искомой величины x sj – будет ли выбранная s-я машинная смена назначена на j-й участок. Поставленная таким образом задача относится к классу комбинаторных задач типа обобщенной задачи о назначении (General Assignment Problem - GAP) [6] . Ее решение путем полного перебора всех возможных план-графиков X потребует временных затрат O(M^S), что неприемлемо для диапазона входных данных. Считая, что количество участков M~100, количество машин N~50 и максимальный срок D~300, получим количество вариантов для перебора M^ND~10^{30 000}.

Таким образом, для реализации данного метода на практике необходимо использовать эффективный алгоритм, работающий за полиномиальное время. К сожалению, доказано [6] , что GAP является NP-полной задачей, т.е. относится к целому классу сводимых друг к другу за полиномиальное время задач, для каждой из которых не известен алгоритм решения полиномиальной сложности. Более того, существует гипотеза, что открытая проблема нахождения алгоритма решения полиномиальной сложности хотя бы для одной NP-полной задачи (что автоматически определяет существование полиномиального алгоритма решения для всех NP-полных задач) не решаема в принципе [9] .

Большинство NP-полных задач эффективно решаются с помощью приближенных алгоритмов, которые по любой наперед заданной погрешности строят алгоритм решения задачи за полиномиальное время, причем полученный результат гарантированно будет отличаться от оптимального не более чем на заданную погрешность. Однако для GAP доказано [6] , что она также является и APX-трудной, т.е. не известен и приближенный алгоритм ее решения полиномиальной сложности для любого наперед заданного коэффициента аппроксимации. Лучшая известная на данный момент оценка аппроксимации [7] :

OPT

e e - 1

+ ε

≤ RES ≤ OPT .

Учитывая вышеизложенный подход, рассмотрим возможный подход к его реализации для построения программно-аппаратного комплекса по автоматизированному планированию лесомелиоративных работ (ПАК ПЛР). При построении такого комплекса будем использовать современные промышленные информационные технологии. Будем строить такой комплекс на основе принципов открытой архитектуры, модульности, наращиваемости, максимальном использовании существующих промышленных решений.

Представим ПАК ПЛР в виде портала с набором веб-сервисов по клиент-серверной архитектуре «тонкий клиент», т.е. обеспечивая многопользовательский авторизованный доступ к функциям ПАК ПЛР по каналу Интернет с любого устройства, в т.ч. не обладающего большими вычислительными мощностями, такого как ноутбук, или планшет, организовав выполнение большей части вычислительных задач на сервере.

Необходимо, чтобы предложенная архитектура серверной платформы обеспечивала сетевое взаимодействие между модулями системы с помощью семейства IP-протоколов и позволяла реализовать механизмы кластеризации и виртуализации на уровне операционной системы для повышения устойчивости, управляемости и балансировки нагрузки системы.

Определим следующие требования к функциональности ПАК ПЛР:

• 1)    отображение исходной ЦКМ в различных режимах с функцией управления слоями;

• 2)    ввод и сохранение исходной информации о планируемых участках и планах по строительству осушительной сети;

• 3)    ввод и сохранение информации о парке машин, в т.ч. возможность ввода автоматизированной информации в систему путем снятия ее с бортового компьютера по поддерживаемому техникой протоколу;

• 4)    расчет и построение графиков прибыли по заданным диапазонам сроков работы с возможностью печати план-графика работ;

• 5)    возможность обновления ЦКМ или внесения ручной корректировки в геопространственные данные.

С учетом вышеизложенного целесообразно рассмотреть следующую архитектурную схему устройства ПАК ПЛР, приведенную на рис. 3. Важно отметить, что для большинства компонентов для создания такой системы (операционной системы с поддержкой кластеризации и виртуализации, системы управления базы данных (СУБД) для управления хранилищем, расширений для СУБД для поддержки геопространственных данных, гео-сервера, HTTP-сервера с контролем прав доступа) существуют промышленные решения на базе открытого программного обеспечения, позволяющие обеспечить ее быстрое конструирование.

В качестве операционной системы оптимальное всего рассмотреть решение на базе Linux, которое обеспечивает высокую производительность, удобность администрирования, возможности по кластеризации и виртуализации.

ПАК ПЛР

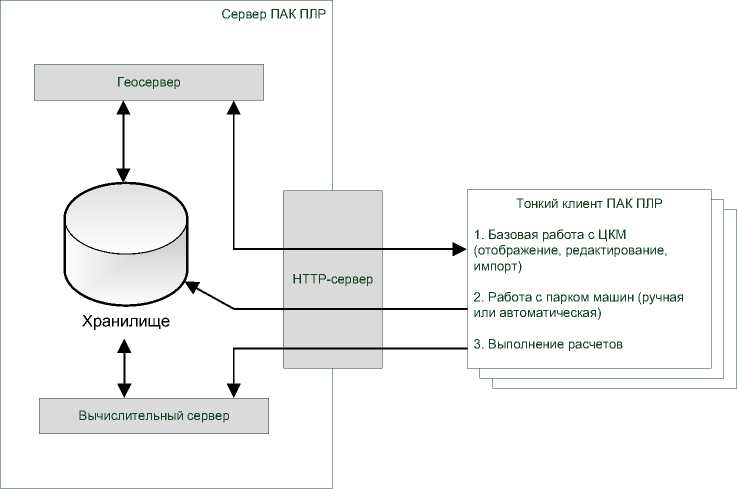
Рис. 3. Архитектурная схема ПАК ПЛР

Для организации HTTP-сервера рациональнее всего использовать Apache HTTP-сервер, который на декабрь 2013 г. использовался на 55,75 % от «Топ 1 000 000», наиболее загруженных сайтов Интернета [9] .

В качестве надежного решения по хранению данной и реализации быстрых запросов целесообразнее всего использовать системы управления на основе реляционных баз данных. Наиболее известным промышленным решением на базе открытого программного обеспечения является PostgreSQL. Следует также отметить, что важным преимуществом PostgreSQL является наличие специализированного модуля расширения PostGIS, добавляющего в PostgreSQL поддержку для работы с геопространственной информацией.

В качестве геосервера наиболее подходящим решением является решение GeoServer, построенное на базе открытого программного обеспечения. GeoServer обеспечивает доступ к геопространственной информации, ее отображение на тонком клиенте через протоколы WMS/WFS, возможность загрузки данных и создания пользовательских слоев.

Вычислительный сервер оптимально реализовать на языке программирования C/С++, что позволит использовать объектно-ориентированный подход при разработке, при этом обеспечивая непревзойденную производительность и возможность по контролю ресурсами.

Выводы

• 1.    Модель, представленная в статье, позволяет:

• -    математически обоснованно определить экономически невыгодные к осушению участки при имеющихся ограничениях на ресурсы;

• -    заложить входные данные (p ijk ) по реальной стоимости выполнения работ не только для каждого типа машин, но и для каждой машины в отдельности. Например, эта возможность может быть учтена при использовании одинаковых машин разных лет выпуска или наличии соответствующей статистики по ремонту машины, которую можно учесть при вычислении реальной стоимости или реальному среднему расходу ГСМ, данные о котором могут быть получены с бортового компьютера. Также она может учитывать регулярные отчисления за использование машин, например, ежемесячную арендную плату или необходимость прохождения ТО;

• -    заложить входные данные (p ijk ) по реальной стоимости выполнения работ в зависимости от участка, опираясь на взятые с исходной ЦКМ данные по грунту. В том числе возможен частный случай задания бесконечной стоимости работ в случаях, когда работа выбранной машины на заданном участке невозможна в

принципе. Также можно задать изменение стоимости в зависимости от смены сезона, например, замерзание грунта может позволить более эффективно проводить отложенные работы;

• -    заложить реальные возможности машин по выработке (w ijk ), также опирающиеся на геопространственную информацию, имеющуюся на ЦКМ. Аналогично в модель могут быть заложены параметры, влияющие на сезонную эффективность производимых работ.

• -    заложить динамические во времени изменения в парке машин, для чего необходимо лишь указать объем выработки w ijk =0 на те дни, когда машина будет недоступна для выполнения работ.

• 2.    Основным преимуществом описанного ПАК ПЛР является то, что комплекс при решении задач оптимизации оперирует огромным количеством информации, большинство которой поступает автоматически и не требует ручного ввода. При этом, опираясь на эти данные, комплекс на основе методов математического моделирования и оптимизации позволяет обеспечить при планировании прогнозирование прибыли, близкое к реальной.

• 3.    Дальнейшие планируемые шаги по изучению поставленной проблемы состоят в обобщении задачи для получения методики, планирования всего цикла работ, включая построение плана осушения, выбора участков для осушения, реализацию полученных результатов на практике.