Выбор оптимального угла наклона солнечных панелей для размещения их в произвольном регионе

Развитие технологий, основанных на возобновляемых источниках энергии, в России идет хорошими темпами [1–3]. Несколько регионов России вышли в лидеры по объему выработки солнечной и ветровой энергии. Ростовская область, например, является лидером по ветряной энергии с общей установленной мощностью ветро-генераторов 170 МВт. При этом Оренбургская область является одним из лидеров по выработке солнечной энергии [4] с общей установленной мощностью солнечных панелей 330 МВт. Энергетические характеристики солнечных станций очень сильно зависят от угла падения солнечных лучей на поверхность солнечных панелей (СП) [5–7]. В данной работе рассмотрено несколько методик расчета углов наклона СП с целью получения максимально возможной выработки электроэнергии. Расчеты выполнены для общего случая в зависимости от даты, угла падения солнечных лучей и географического местоположения солнечной станции.

Моделирование

В работе рассматривается модель для определения почасовой солнечной инсоляции на наклонных поверхностях, имеющих различный угол наклона и ориентацию. Примем допущение, что расчет ведется без учета диффузии, отражения и рассеяния солнечных лучей. Для выбора оптимального угла наклона СП, вычисленного по разным методикам, можно не учитывать влияние атмосферных явлений, которые сказываются только в ко- нечном итоге на объеме выработки солнечной энергии. Это допущение будет устранено в следующих исследованиях.

Поток излучения на горизонтальную поверхность по [8] с учетом зенитного угла, даты и времени суток определяется как

I              ( ³⁶⁰ n II

G„ I = ст 1 + 0,033 cos         cos 6„ _k,    (1)

n , k       sc                                             n , k

V            V 365 77

где ст sc - солнечная постоянная, принимаемая в расчетах равной 1367 Вт/м² [8];

n – порядковый номер дня в году, начиная с 01 января;

6 n k - зенитный угол, т. е. угол падения солнечного луча излучения на горизонтальную поверхность согласно рис. 1;

k – количество точек расчета в промежутке времени между восходом и закатом солнца.

На рис. 1 показан зенитный угол θ, угол солнечной высоты α _s , угол наклона СП β, угол солнечного азимута γ _s , азимутальный угол расположения поверхности СП γ относительно направления – юг.

Зенитный угол согласно [8] определяется по выражению

6 _nk = arc cos ( cos 5 _n cos ф cos го _k + sin 5 _n sin ф ) ,   (2)

где ф - широта расположения СП;

δ _n – координата солнца на небесной сфере (угол склонения), определяемая по выражению (3) для n -го дня в году;

го к - часовой угол, рассматриваемый в дан-

Зенит

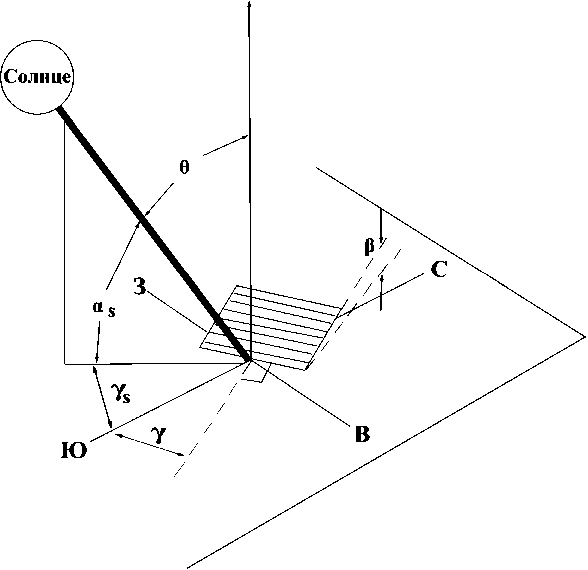
Рис. 1. Наглядное изображение солнечной панели в пространстве Fig. 1. A representation of a solar panel in space

ный момент времени в течение светового дня, определяемый по выражению (4).

Угол склонения δ n равен угловому расстоянию на небесной сфере от плоскости небесного экватора до светила, и определяется согласно [8–10]

по уравнению

5 n = 23,45sin l 360

284 + n n ^ 365 180 J ^.

Часовой угол – это угловое расстояние, измеренное вдоль небесного экватора на запад от небесного меридиана (той его части, которую светила пересекают в момент верхней кульминации) до часового круга, проходящего через избранную точку на небесной сфере. Он определяется согласно [11, 12] как

ю k = 15 7^ t a — 12 ) , 180

где t_а – это видимое или истинное солнечное вре-

мя, которое определяется ежедневным видимым движением истинного или наблюдаемого солнца, которое находится по выражению (5), ч.

Используя [12, 13], выполнив некоторые преобразования, получим

t

а

= t k

+ EOT n ± 4 Г5 T .. -X )

где t_k – местное время в рассматриваемый мо-

мент, ч;

EOT n – разница во времени между кажущимся солнечным временем и средним солнечным временем, определяемая по выражению (6) (значение зависит от номера дня в году), мин;

T_GMT – часовая разница между нулевым меридианом и рассматриваемой местностью, ч;

λ – долгота местности, град.

Отрицательное значение перед скобкой в выражении (5) принимается при положительном ме-

ридиане, а положительное – при отрицательном.

Уравнение времени согласно [8] определяется

EOT n = 9,87 sin ( 2 B _n ) - 7,53cos ( B _n ) -

-1,5sin (Bn), где Bn – число, зависящее от номера дня и находится по выражению

в

(6) году,

на юг. Если СП ориентирована строго на юг, то угол γ = 0 (см. рис. 1) .

Согласно [14] угол наклона СП β в зависимости от номера дня и широты местности может быть определен как

Р„=ф- 1,55-^n^.(8)

n180

Оптимальный угол наклона СП β в час, когда солнце находится в зените, для любого дня согласно [8] можно вычислить по выражению

Pn = Mn|.(9)

Выражения (8) и (9) могут быть использованы в математических моделях, если СП стационарно закреплена и направлена строго на юг, а угол наклона СП β не изменяется в течение всего дня. По истечении суток (или реже) его можно изменить (подкорректировать), предварительно вычислив по выражению (8) или (9) для нужного номера дня.

Если регулирование угла наклона поверхности СП не планируется, то при монтаже солнечной станции его выбирают в зависимости от широты местности согласно [15] равным:

P = 2 ф при 1 ° < ф <  6 °

P = 1,75 ф при 6 °<ф< 9 °

<Р = 1,5 ф при 9 °<ф< 12 ° .             (10)

Р = 1,25 ф при 12 °<ф< 15 °

Р = ф при ф >  15 °

В случае если необходимо получить максимальное фотоэлектрическое преобразование, нужно поверхность СП регулировать в двух плоскостях. Поэтому необходимо СП вращать относительно и второй оси – азимута (при этом угол азимута будет всегда равным у = у _s ), одновременно изменяя угол наклона β СП относительно склонения солнца в течение всего светового дня. Такой угол будет находиться по выражению для произвольного дня:

Р _nk = arccos ( cos ф cos 5 _n cos ю _k + sin ф sin 5 _n ) , (11)

360 ( n - 81 ) П

B„ =-- n 365    180

.

Для получения максимального фотоэлектрического преобразования в СП необходимо, чтобы лучи солнца падали прямо перпендикулярно ее поверхности. Поэтому СП необходимо располагать в любой момент времени под прямым углом к лучам солнца в течение всего светового дня. Для ориентации СП относительно солнца можно использовать две оси регулирования. Одна ось – это ось регулирования относительно склонения (угол β), другая ось – относительно азимута (угол γ _s ). При этом текущий угол СП относительно азимута будет равен γ , при условии, что СП не ориентирована

где ю _k - часовой угол, определяемый по выражению (4) для произвольного момента времени t_k

межу восходом и закатом солнца;

5 _n - склонение солнца в n -й день.

Времена восхода t ₁ и заката t ₂ солнца находят-

ся по выражению

t 1,2

12 ±Ю ^ ^- ^EOTn ± 4^a ( ^15OTGMT -^X) ₍₁₂₎

15 180             60           ,

где ω s – часовой угол на закате солнца, рад.

Минус в выражении (12) перед ω s соответствует нахождению времени восхода солнца. Плюс – заката за горизонт. Отрицательное значение перед скобкой в выражении (12) 4 ° ( 15 ° T G_MT -X )

принимается при положительном меридиане, а положительное – при отрицательном. Часовой

угол на закате находится по следующему выражению [8]

to s = arccos ( - tg 5 tg ^ ) .                      (13)

Азимутальный угол находится по выражению [16]

Y s = sign ro k

[ cos 9 sin ф- sin 5„ arccos I------------------ (     sin 9 cos ф

где sign to _k - функция, определяющая знак перед

выражением.

Тогда поток излучения с учетом зенитного

угла на горизонтальную поверхность, угла наклона СП β, даты и времени суток, общем случае, будет

определяться как

G_{n к} = gJ 1 + 0,033cos I      I I cos(9„_k-p„_k), (15)

n , k      sc                                           n , k     n , k

где P _n , _k - угол наклона СП в зависимости от но-

мера дня n при его изменении в течение суток от времени для времени восхода t ₁ и заката t ₂ солнца. При нахождении потока для углов, не зависящих от времени суток, индекс k в формуле (15) можно опустить.

вычисленный по формуле (8), будет изменяться от 80 до 9,8°. Для оценки влияния этих углов на эффективность работы СП на рис. 3 представлен результат расчета потока солнечной энергии на наклонную плоскость СП для дня летнего солнцестояния без учета влияния атмосферных явлений. В день летнего солнцестояния продолжительность светлого времени суток для г. Оренбурга составляет 16 ч 27 мин 32 с.

Среднесуточное глобальное солнечное излучение на горизонтальной поверхности можно найти согласно [8, 17] по среднемесячному ежедневному глобальному излучению. Среднесуточное глобальное солнечное излучение, падающее на поверхность СП, в периоде между восходом и закатом солнца, с учетом ее угла наклона и без учета влияния атмосферных явлений может быть найдено по выражению

12 I            ( 360 и п ||

I = о    1 + 0,033 cos             х

°’n п sc I             I 365 180 JJ x^cos (ф-Рn k) cos 5n (sin to2 - sin ro1) +

+

Результаты исследования

На рис. 2 представлена зависимость углов наклона β СП, вычисленных по вышеприведенным выражениям от номера дня в году для момента времени, когда солнце находится в зените (солнечный полдень).

Из расчетов видно, что угол наклона β СП, вычисленный по формулам (9) и (11), совпадает и в полугодие меняется от 74 до 28°. В другое время суток эти углы будут разными. Угол наклона,

n ( to ₂ -to 1 )

sin ( ф-Р n , k ) sin 5 n

где ω 1 , ω 2 – часовые углы, определяемые по выражению (4) для времени восхода t 1 и заката t 2 солнца.

Формула (16) справедлива в случае, когда угол СП β в течение суток не изменяется.

На рис. 4 приведено значение солнечной инсоляции в зависимости от номера дня в году в г. Оренбурге, приходящейся на горизонтальную поверхность СП, с различными, неизменными в течение суток, углами наклона.

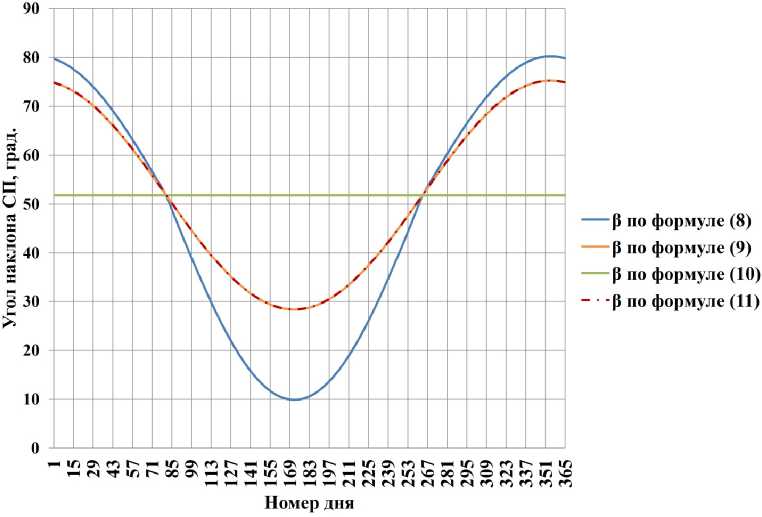
Рис. 2. Зависимость угла наклона СП от номера дня в солнечный полдень

Fig. 2. Dependence of the angle of inclination on the day of the year on a sunny afternoon

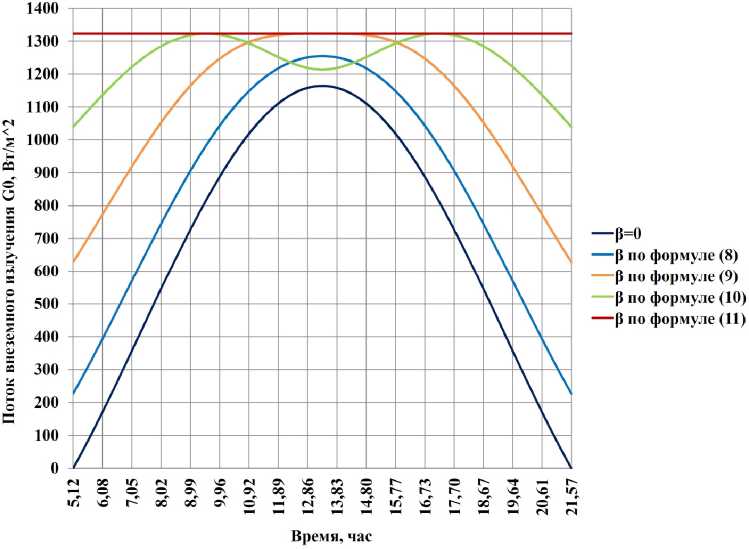
Рис. 3. Зависимость потока излучения от времени суток для дня летнего солнцестояния (171-й день) с учетом угла наклона

Fig. 3. The dependence of the radiation flux on the time of day for the summer solstice (day 171), taking into account the angle of inclination

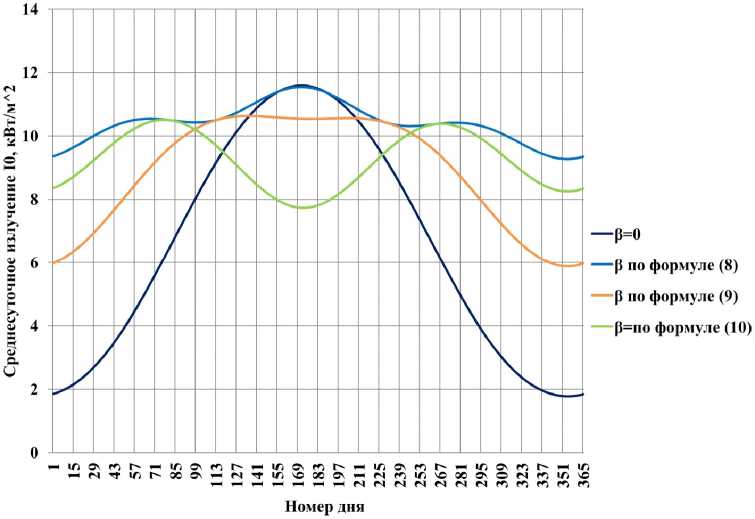
Рис. 4. Зависимость среднесуточного солнечного излучения от номера дня в году с учетом угла наклона

Fig. 4. The dependence of the average daily solar radiation on the day of the year, taking into account the angle of inclination

Выполнив расчеты, получаем, что наиболее оптимальным углом является изменяемый угол наклона СП по двум осям, вычисленный по формуле (11). Расчеты показывают эффективность работы СП при ежесуточной установке угла на- клона СП, вычисленного по формуле (8). В результате исследования установлено, что эффективность работы СП, установленной под углом, вычисленным по формуле (8), незначительно ниже, чем при угле, вычисленном по формуле (11)

(разница больше в зимние месяцы). Угол наклона СП, вычисленный по формуле (8), можно использовать для СП, не имеющих возможностей двухосевого регулирования. В зимние месяцы оптимальным углом можно считать и угол, вычисленный по формуле (10), но в летние месяцы выработка электроэнергии СП, расположенной под этим углом, будет значительно меньше. С некоторым допущением можно считать, что углы наклона СП, вычисленные по формуле (9), являются оптимальными в течение всего года, если нет возможности регулирования углов наклона ни по одной из осей.

Заключение

В работе был выполнен анализ способов вычисления оптимального угла наклона СП по различным литературным источникам. По результатам исследования можно сделать вывод о том, что регулирование угла наклона по двум осям является наиболее эффективным способом повышения эффективности работы СП независимо от сезона. Поэтому задача создания экономичных, простых в управлении и эксплуатации двухкоординатных систем слежения за солнцем является актуальной.