Выбор оптимального управления перелетом космического аппарата с электроракетной двигательной установкой к точке либрации L1 системы Земля-Луна

Луна - это естественный спутник Земли, исследование и освоение ресурсов которого может приносить не только новые научные знания, но и практическую выгоду. Одной из главных проблем освоения Луны является высокая стоимость доставки грузов на селеноцентрические орбиты. Применение перспективных электро-ракетных двигателей в качестве базы для маршевой двигательной установки на космических аппаратах, функционирующих в системе Земля-Луна, позволит повысить эффективность транспортных операций. Высокая скорость истечения реактивной струи, характерная для двигателей малой тяги [1], обеспечивает значительно меньший расход рабочего тела по сравнению с двигателями на химическом топливе. Это позволяет уменьшить массу рабочего тела и объем баков для его хранения а, следовательно, стартовую массу космического аппарата (КА) и затраты на осуществление перелетов. Некоторые технические особенности двигателей малой тяги и теоретические аспекты поиска оптимальных законов управления описаны в статьях [2-6].

Однако, низкий уровень тяги, создаваемый двигательными установками такого типа, приводит к значительным длительностям перелётов. Например, перелет КА SMART-1 Европейского космического агентства с низкой околоземной на низкую окололунную орбиту длился более 450 суток. При выборе типа двига-

тельной установки для осуществления миссий, необходимо знать какова будет минимально возможная длительность манёвра, не превысит ли она заданные ограничения? Решение задачи об оптимальном по быстродействию перелёте позволит ответить на эти вопросы.

В статье рассматривается методика оптимизации перелётов c заданной околоземной орбиты к точке либрации L1, в окрестности которой планируется размещение посещаемой международной станции. На движение космического аппарата в окрестности точек либрации гравитационные поля Земли и Луны оказывают практически равнозначное воздействие, поэтому законы программного управления необходимо получать в рамках ограниченной проблемы трех тел.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ КА И ОПТИМАЛЬНОЕ ПО БЫСТРОДЕЙСТВИЮ

УПРАВЛЕНИЕ

Движение аппарата описывается в инерциальной полярной барицентрической системе координат (рис. 1). Основная плоскость совмещена со средней плоскостью движения Луны, центр координат находится в барицентре системы Земли-Луна, полярная ось направлена в сторону точки весеннего равноденствия. Считается, что КА движется под действием гравитационных полей Земли и Луны, которые вращаются вокруг общего барицентра по плоским круговым орбитам с постоянной угловой скоростью. Влияние нецентральности Земли и Луны, а также атмосферы Земли и гравитации других небесных тел не учитывается.

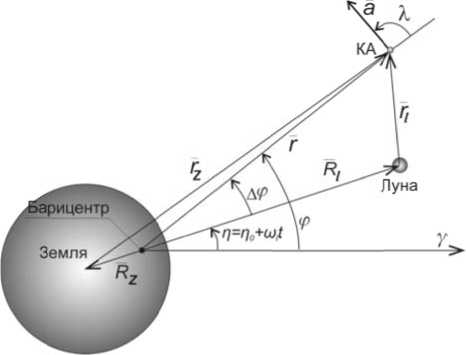
Рис. 1. Инерциальная полярная барицентрическая система координат

где p l = 0,0123 - отношение массы Луны к суммарной массе системы Земля-Луна; a ₀ – номинальное безразмерное ускорение от тяги двигателей; с – безразмерная скорость истечения рабочего тела; 5 - функция включения-выключения двигателей; m = m _PT/ m ₀ - относительный расход топлива.

Заменим в (1) угол ф на угол Луна - барицентр - КА по формуле Д р = р-ц . Дифференциальное уравнение, описывающее изменение этого угла примет вид:

d (.^ф- Ф_т из.

dt r

В этих обозначениях расстояния от КА до

Вектор реактивного ускорения от тяги двигателей лежит в основной плоскости, его величина зависит только от массы КА. Не учитываются изменения величины тяги при изменении светотеневой обстановки на орбите, деградации энергоустановки, а также особенностей углового движения КА. Направление реактивного ускорения задается углом Х ( ) , который отсчитывается от барицентрического радиус-вектора против часовой стрелки. Положение Земли и Луны определяется постоянными по величине радиус-векторами R z и R l и углом ц, имеющим постоянную скорость изменения щ , равную средней угловой скорости движения Луны относительно барицентра. Положение центра

Земли r _z и Луны r_l равны соответственно: r_Z = д/ r ² + R Z + 2 • r • R Z • cos ( Д ф ) , r l = д/ r ² + R 2 — 2 • r • R l • ео8 ( Д ф ) .

Выбор программного управления проводится с использованием в качестве критерия оптимальности минимального времени перелёта:

T

T _ J dt ^ min .             (3)

масс КА определяется радиус-вектором r и полярным углом ф .

Все фазовые координаты системы приводятся к безразмерному виду. Для этого все линейные расстояния относятся к среднему расстоянию между центрами Земли и Луны d _z - _l = 3 84400 км, скорости – к средней скорости Луны относительно барицентра, ускорения – к гравитационному ускорению на орбите Луны, время – к среднему периоду обращения Луны, угловые величины переводятся в радианы. В этом случае уравнения движения имеют следующий вид:

[ dr = v dt     rъ а- _ Уф

Введем в ра с смотрение вектор фазовых координат КА X = ( r, Дф , V_r, У _ф , m ) , который подчиняется граничным условиям, соответствующим цели перелёта и возможным о граничениям; вектор функций управления u ( t ) = ( Л (t ), 5 (t )) T g U , где U - область воз м ожных значений функций управлений и p = ( a ₀, c ) T - вектор проектных параметров КА.

Формально задача оптимизации описывается следующим образом: требуется определить вектор функций управления, удовлетворяющий граничным

условиям, уравнениям движения (1-2) и доставляю-

щий минимум критерию опти м аль н ости (3):

( t ) = arc min T ( u\p, X ₀, X K = fixe ) .

и . opt

u ( t ) g U

В соответствии с формализмом принципа максимума Понтрягина вводим вектор сопряженных переменных P = ( P r , Р дф , P_v , Р_{У ф} , P m ) и формируем функцию Гамильтониана

dt dVr dt

, r у 2

r ф

r

—

( 1 ^— R i ) "

r + R Z • cos ( — — n )

r z

—

R i '⁽ r — R i • cos ⁽ - — n ))

• P . Из условия максимума Гамиль-

аУ ф dt

—

r3

у .у

V-V- + ( 1 — R i ) "

+ a r ,

R z ' sin ^- ф -n )

—

r

R l • R ■ sin (уф — n )

3 r_Z

dm _ a ₀ • 5

dt c

rl ar _ a5

^{+ a} ф ^,

^ao "  ⁵

• cos Z, a _ -    " sin Z, ф   (1 — m)

тониана определим оптимальное направление вектора ускорения X _opt ( t ) и функции включения- выключения двигателей:

PV                    PV sin ^opt = /    . ф . , cos ^opt = ,    . r , , (5)

Py + P          P^ + Pv r        фр                           r        фр

5 = ^

0), . 1,

Д< 0 p   J Pv ² + Pv ²

, Д = P m +     r ^ф

Д >  0 c 1 - m

Система сопряжённых уравнений, согласно

принципу максимума определяется соотноше-

dP  дH нием —— = -—= и имеет вид: dt    дX

dP dP = — . dt     ^Vr

^ V » ²1 .Pi 3. ( ^{1 -} P i M ^{r +} R z ' cosA ^ ) ² ~⁺~+~-----

^ r г r              r z

3. P i •( ^{r -} R i ■ ^{cos A} » ^{) 2} ) p V »

5           ⁺ P » 2 ⁺

Г ) r

+ P

V »

( V V » 3. R_z . ( 1- p_i ) -sinA » - ( r + R_z ■ cosA » )

Г ^ ⁺             r ⁵

3. p_i . R sinA » . ( r - R . cosA » )

dP » = P . dt     ^Vr

r ⁵

I. R z ^"^,A » ₊ r z

-

+

3. ( 1 - p_i ) . r . R_z ■ sinA » . ( r + R_z ■ cosA » )

^r z

+

p -R . sinA » 3. p . r . R . sinA »■ ( r - R ■ cosA » )

r ³

r ⁵

+

+ -

V »

R_z . cosA » p . R_i . cosA »

^r z

r ³

+

+

rz5

r ⁵

dP         V

-= =- P + P -» dt             » r

ЯР P .V -7.p -V -P

^UP V » = ^P V » V ² P V r V » ^r » dt             r

dP- m dt

a ₀ -3

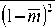
² -vp² V PV r ⁺ PV » ’

Значение относительного расхода рабочего тела в момент старта равно нулю (рабочее тело еще не израсходовано). Для задачи на оптимальное быстродействие расход рабочего тела в конечный момент времени не фиксирован и согласно условию трансверсальности P m (T ) = 0 .

dP

Согласно уравнениям (5-7) ---< 0, при всех dt

t е ( 1 0 , T ), поэтому при всех t е ( 1 ₀, T ) , P m ( t ) >  0 . Поэтому, согласно (6), при всех t е ( 1 ₀, T ) функция включения-выключения двигателей § ^ 1 , то есть двигатель работает без выключений, кроме, может быть, конечной точки траектории, в которой возможно § ( T ) = 0, что соответствует выключению двигателя в момент завершения движения.

Кроме того, в силу монотонного убывания функции P m ( t ) , удобно использовать эту сопряженную переменную для выхода из интегрирования. Остальные сопряженные переменные и фазовые координаты могут изменяться немонотонно, а минимальная длительность перелета для заданных проектных параметров заранее неизвестна.

Таким образом, задача об оптимальном по быстродействию плоском движении в системе Земля-Луна сводится к следующей двухточечной четырехпараметрической краевой задаче: требуется найти такие начальные значения сопряженных переменных, чтобы на концах оптимальной траектори и выпол н яли с ь нача л ьное и конечное условия X ( t ₀ ) = X ₀ , X ( t ) = X K . Для задачи достижений точки либрации L1 конечные значения вектора фазовых координат задаются с ледующим образом:

X . = ( R l 1 , Д » , = 0, V r, = 0, V„ = V » L 1 ) ^T , здесь V ^ L 1 = 0,8477 - безмерная скорость точки либрации L1, R L 1 = 0,8369 - безразмерное расстояние между точкой либрации L1 и барицентром.

Для решения поставленной краевой задачи использовалась модификация метода Ньютона, описанная в работе [5], и метод продолжения по параметру [6]. В качестве начального приближения для решения краевых задач использовались значения, вычисленные по аппроксимационным зависимостям, полученным в [5] в рамках задачи двух тел (без учета гравитации Луны) при не фиксированной суммарной угловой дальности перелета. Метод продолжения по параметру, подробно описанный в [6], был использован для получения требуемых решений в рамках ограниченной задачи трех тел. В качестве изменяемого параметра использовался параметр p l - отношение массы меньшего притягивающего центра к суммарной массе системы.

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ И ОПТИМИЗАЦИИ ДЛЯ ЗАДАЧИ

ДОСТИЖЕНИЯ ТОЧКИ ЛИБРАЦИИ L1

Проектные параметры аппарата выбраны близкими к параметрам исследовательского КА Европейского космического агентства SMART-1: m = 400 кг, P = 0,1 Н, c = 15 км/с. Рассматривается перелет КА с круговой барицентрической орбиты радиусом r₀ = 100000 км в точку либрации L1 системы Земля-Луна. Система уравнений (1-2, 5-7) интегрировалась методом Рунге Кутты четвертого порядка. Краевая задача решалась до достижения суммарной погрешности по краевым условиям 0,001%.

При решении задачи использовалась следующая методика.

1. В качестве начальных приближений для сопряженных множителей использовались значения, полученные в результате решения задачи об оптимальном по быстродействию перелёте между круговыми, компланарными орбитами без учета гравитации Луны [5]. В этом случае, согласно условию трансверсальности для угловой дальности Р _{Д р} ( T ) = 0, что при p l = 0 в любой

момент времени, согласно второму уравнению (7) приводит к Р^_ф ( t ) = 0 и порядок краевой задачи снижается до трёх.

• 2.    Используя метод перемещения по параметру ^ l от ^ = 0 до ^ = 0,0123, определяется изменённый вектор начальных значений сопряжённых множителей, соответствующее управление и траектория движения с учетом гравитации Луны с нефиксированной конечной угловой дальностью КА-Луна (достигается значение А ф ( Т ) = Аф* ).

• 3.    Условие трансверсальности в конечный момент времени Р _{А ф} ( Т ) = 0 заменяется на условие достижения требуемой угловой дальности КА-Луна Аф(Т ) = Аф , осуществляется процедура метода продолжения по параметру Аф (Т ) от А ф к А ^_ = 0 и получаются оптимальное управление и соответствующая траектория движения при требуемых граничных условиях.

На рис. 2 -5 приведены полученные с использованием этой методики оптимальная програм- ма управления, изменение компонент скорости КА и соответствующая траектория движения.

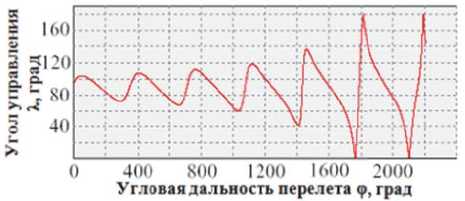
Рис. 2. Оптимальная программа управления углом направления вектора тяги

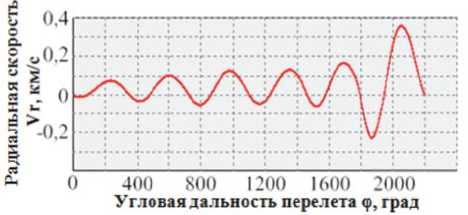
Рис. 3. Изменение радиальной составляющей скорости Vr

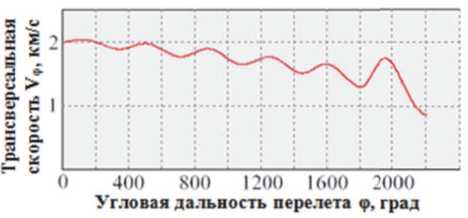
Рис. 4. Изменение трансверсальной составляю- щей скорости Vф

Длительность оптимального перелёта зависит от относительного углового положения

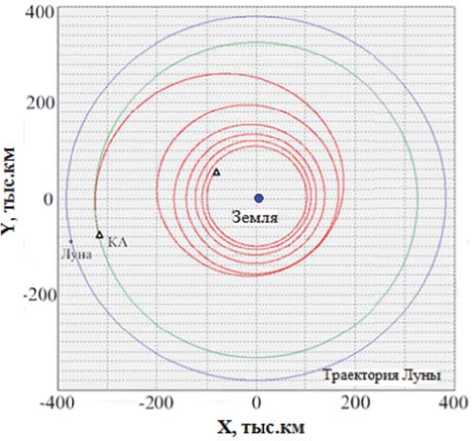
Рис. 5. Оптимальная траектория достижения точки либрации L1

между Луной и КА в момент старта, на рисунке 6 приведена эта зависимость. Полученные данные показывают, что наилучший результат для КА с такими проектными параметрами 41,95 сут достигается, когда начальный угол между КА и Луной равен 147,7 град.

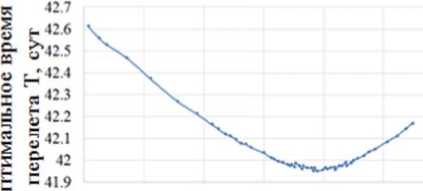
О 70     90     110     130     150    170     190

Начальное угловое положение КА <ро. град

Рис. 6. Зависимость оптимального времени перелета от начального углового положения КА

Найденное оптимальное относительное угловое положение КА и Луны позволяет определить наилучшую дату начала движения, которая в рамках рассматриваемой круговой ограниченной задачи трех тел будет повторяться один раз за лунный месяц.

ЗАКЛЮЧЕНИЕ

Предложенная авторами методика, основанная на формализме принципа максима Понтрягина и методе продолжения по параметру, продемонстрировала свою эффективность при решении задач об оптимальных по быстродействию перелётах КА с электроракетными двигателями к точке либрации L1 системы Земля-Луна для различных граничных условий и проектных параметров КА. Кроме того, данная методика легла в основу разработанного программного комплекса, позволяющего автоматизировать процесс выбора оптимального по быстродействию управления и соответствую-  3.

щей траектории движения, которые могут быть использованы для проектно-баллистического анализа транспортных операций КА с ЭРДУ в системе Земля-Луна.                             4.

Результаты, представленные в статье получены в рамках выполнения государственного задания Минобрнауки России 9.5453.2017/8.9.