Выбор оптимальной структуры автокодировщика с применением методой байесовской оптимизации
Автор: Бишук А.Ю., Бахтеев О.Ю.
Журнал: Труды Московского физико-технического института @trudy-mipt
Рубрика: Информатика и управление
Статья в выпуске: 3 (67) т.17, 2025 года.
Бесплатный доступ
В работе рассматривается задача выбора структуры модели автокодировщика. Под автокодировщиком понимается дифференцируемая по параметрам модель, представимая в виде композиции двух функций: кодировщика, представляющего входной объект в виде скрытого векторного представления, и декодировщика, преобразующего скрытое векторное представление в исходное признаковое пространство. Структура модели автокодировщика представляется в виде набора гиперпараметров, для выбора которых предлагается применять методы байесовской оптимизации. Предлагается двухэтапная модификация метода байесовской оптимизации: на каждой итерации поиска выбирается множество точек с наилучшей оценкой качества модели, а затем из них отбирается наилучший с учетом динамики обучения. Приводится теоретическое обоснование алгоритма, а эксперименты на выборках CIFAR и Fashion-MNIST подтверждают эффективность предложенного подхода.
Байесовская оптимизация, оптимизация гиперпараметров, нейронные сети, AutoML, KDE, TPE, автокодировщик, выбор структуры модели
Короткий адрес: https://sciup.org/142245834
IDR: 142245834 | УДК: 519.25, 519.7
Текст научной статьи Выбор оптимальной структуры автокодировщика с применением методой байесовской оптимизации
Оптимизация архитектуры и гиперпараметров автокодировщиков остается важной и сложной задачей в области машинного обучения. Под автокодировщиком понимается нейронная сетв, состоящая из двух частей — кодировщика и декодировщика, которая используется для обучения эффективных представлений данных без учителя. В фундаментальном
(с) Вишук А. Ю., Бахтеев О.Ю., 2025
(с) Федеральное государственное автономное образовательное учреждение высшего образования
«Московский физико-технический институт (пациопальпый исследовательский университет)», 2025
2. Постановка задачи
исследовании трудностей обучения глубоких сетей [1] было показано, что выбор гиперпараметров существенно влияет на качество работы модели. Для автокодировщиков эта проблема особенно актуальна, поскольку качество получившихся сжатых представлений сильно зависит от выбранной структуры сети, характеризующейся количеством слоев и их параметрами, размером скрытого представления и другими.
Ранее было предложено несколько специализированных методов оптимизации гиперпараметров глубоких сетей. Например, был разработан алгоритм поиска архитектуры на основе мета-обучения [2], а также для этой задачи были адаптированы [25] древовидные структуры Парзена и разработан подход [4], использующий экстраполяцию кривых обучения для предсказания конечного качества модели. Однако эти методы либо требуют значительных вычислительных ресурсов, либо не учитывают важные особенности динамики обучения конкретных моделей, например, автокодировщиков.
Классические методы оптимизации гиперпараметров, такие как полный перебор [5] и случайный поиск [16], демонстрируют ограниченную эффективность при работе с большими пространствами гиперпараметров. Более перспективным направлением стала байесовская оптимизация [7], которая строит вероятностную модель целевой функции. Развитие этого подхода привело к созданию различных модификаций, включая гауссовские процессы [8] и методы на основе древовидных структур [25].
Несмотря на значительный прогресс в области байесовской оптимизации и нейроархи-тектурного поиска (NAS) [11], существующие методы имеют несколько принципиальных ограничений применительно к задаче настройки автокодировщиков. Во-первых, большинство подходов, включая современные методы NAS [12], разрабатывались преимущественно для однонаправленных архитектур и не учитывают специфику двунаправленной структуры автокодировщиков [13]. Во-вторых, традиционные методы требуют полного обучения модели для точной оценки качества, что вычислительно дорого для глубоких автокодировщиков. В-третьих, они не учитывают динамику изменения функции потерь на ранних этапах обучения, которая содержит важную информацию о потенциальном качестве модели [14]. Следует отметить, что существуют альтернативные подходы к оптимизации архитектур автокодировщиков, такие как эволюционные алгоритмы [23], однако они требуют значительных вычислительных ресурсов и не обеспечивают теоретических гарантий сходимости.
В нашей работе предлагается новый метод байесовской оптимизации, специально разработанный для настройки гиперпараметров автокодировщиков. Данный подход сочетает двухэтапный отбор кандидатов с анализом динамики обучения на ранних итерациях. На первом этапе отбирается множество перспективных наборов гиперпараметров, на втором — производится их уточнение на основе признаков, извлекаемых после одной эпохи обучения.
Эксперименты на стандартных наборах данных CIFAR [9] и Fashion-MNIST [10] 1 показывают, что предложенный метод превосходит по эффективности базовые подходы байесовской оптимизации для автоэнкодера. В частности, предлагаемый алгоритм демонстрирует более быструю сходимость и позволяет экономить до 60% вычислительных ресурсов при сохранении качества результатов. Эти преимущества особенно важны для практических применений, где требуется частая настройка гиперпараметров автокодировщиков в условиях ограниченных ресурсов. Основной вклад работы заключается в разработке специализированного алгоритма оптимизации гиперпараметров автокодировщиков, его теоретического обоснования, а также экспериментального подтверждения эффективности на стандартных наборах данных.
В данной работе рассматривается задача выбора гиперпараметров модели автокодировщика, задающих его структуру. Пусть задана выборка X С R”, где R” — признако- вое пространство. Выборка разделена на обучающую частв Xtrain и валидационнуто частв Xvalid- Обучающая частв выборки Xtrain исполвзуется для оптимизации параметров автокодировщика, а валидационная частв Xvaiid, размера М, для ввйора гиперпараметров. Под автокодировщиком понимается параметризованная моделв fh, заданная композицией двух отображений:
fh(w)= f^(wd) о fh(we): Rn ^ R”, где fe : Rn ^ Rm — кодировщик с параметрами we и структурой, задаваемой вектором гиперпараметров he, fd : Rm ^ Rn — декодировщик с параметрами wd и структурой, задаваемой вектором гиперпараметров h^, Rm — скрытое пространство (т ^ п). Оптимизационная задача для базовой модели автокодировщика выглядит следующим образом:
ОД= Е ||fh(x) - xl2 ^ w.R , хеХи™ где w — вектор параметров автокодировщика, образованный конкатенацией векторов we и wd, h вектор гиперпараметров, образованный конкатенацией векторов he и hd. Заметим, что к модификациям базовой модели автокодировщика относятся также порождающие модели различных классов, включая вариационные автокодировщики [25] и диффузионные модели [26].
Задача оптимизации гиперпараметров формулируется как задача выбора вектора гиперпараметров h* G H, минимизирующего целевую функцию L(h) для валидационной вы борки Xyaiid- характеризующую качество работы модели на данных. Здесь H представляет пространство допустимых гиперпараметров, которое может включать как непрерывные, например, скорость обучения, так и дискретные параметры, например, количество слоёв.
Ключевая сложность задачи заключается в том, что функция L(h) не имеет аналитического выражения, а её оценка требует дорогостоящей процедуры обучения модели. Кроме того, L(h) в общем случае является невыпуклой, многоэкстремальной и может содержать шум, связанный со стохастичностью обучения. Эти свойства исключают применение базовых методов оптимизации и требуют специальных подходов.
2.1. Байесовский выбор гиперпараметров
В рамках байесовского подхода задача оптимизации гиперпараметров модели формулируется как задача нахождения апостериорного распределения:
P(h|Xva lid)
P(Xvalid|b)Xh) p(Xval id)
где p(h) — априорное pаспределение, p(Xvaiid|h) _ правдоподобие данных, p(Xvalid) _ маргинальное правдоподобие.
Оптимальные гиперпараметры находятся как:
h* = arg maxheHp(h|Xvai i(l).
На практике прямое вычисление апостериорного распределения затруднительно, поэтому используются различные методы аппроксимации, включая методы Монте-Карло [15] и суррогатные модели [16]. Для оценки плотности многомерной величины p(h|Xvaпа) применяется ядерная оценка плотности KDE [25], которая позволяет аппроксимировать распределение p(h|Xvaы) без строгих предположений о его форме. Для выборки {hi}”=1 опенка плотности имеет вид
1 \Д vhh — h* ^ p(h) = —h X K — ’ nwn ^^ \w i=1
где K : Rh ^ R+ — ядерная функция (обычно гауссова), w > 0 — шири на окна, h — размерность пространства гиперпараметров. KDE находит применение как для построения априорных распределений, так и для анализа пространства гиперпараметров [17].
Основные преимущества KDE в контексте байесовской оптимизации включают непараметрический характер оценки и способность адаптироваться к сложным многомодальным распределениям, что особенно важно при работе с нерегулярными пространствами гиперпараметров.
2.2. Метод Tree-structured Parzen Estimator (ТРЕ)
В контексте байесовской оптимизации с использованием KDE возникает ключевая проблема: традиционные методы оценивают единое распределение p( h | Xvai id); что может быть неэффективно для многоэкстремальных функций. Метод Tree-structured Parzen Estimator (ТРЕ) [25] формулирует задачу оптимизации гиперпараметров в терминах условных вероятностей. В отличие от стандартного байесовского подхода, ТРЕ строит раздельные распределения для векторов гиперпараметров с низким значением функции потерь и с высоким. Пусть у — квантиль, разделяющий наблюдения на две группы: 5+ = { h j|T( h j) < Т7} и S- = { h j|T( h j) > Т7}. Алгоритм моделирует распределения:
P(h|T) = |
если T (h) < Т7, иначе,
h
new
= argmaxhE1! (h) = arg maxh
p+( h )
P-(h)
Это позволяет эффективно балансировать между исследованием новых областей и уточнением уже найденных перспективных наборов гиперпараметров.
3. Предлагаемый метод
В данном разделе представлен новый алгоритм байесовского выбора гиперпараметров автокодировщиков, сочетающий идеи стохастической оптимизации и слабоконтролируемого обучения [18]. Метод основан на двухэтапной процедуре, где сначала отбираются кандидаты для старта обучения, а затем по первым эпохам определяется лучший вариант для полного обучения. Основной вклад заключается в использовании промежуточных показателей после короткого обучения моделей-кандидатов, что позволяет сократить общие вычислительные затраты по сравнению с базовым подходом.
3.1. Описание метода
Предлагаемый метод решает ключевую проблему традиционных подходов к подбору гиперпараметров — необходимость полного обучения множества моделей-кандидатов перед принятием решения об их качестве. Вместо этого мы предлагаем адаптивную стратегию, где решение о перспективности тех или иных гиперпараметров принимается на основе их поведения после ограниченного числа шагов обучения.
Основная гипотеза, лежащая в основе метода, заключается в том, что динамика изменения функции потерь на ранних этапах обучения содержит достаточно информации для прогнозирования конечного качества модели. Это позволяет существенно сократить вычислительные затраты, избегая полного обучения заведомо неперспективных наборов гиперпараметров.
Пусть задано пространство гиперпараметров H С Rh и функция потерь L( h , T), оценивающая качество модели после T эпох. Для каждого кандидата h вычисляются динамические признаки u = u ( h , k) G Rs после k ^ T эпох обучения. Метод решает задачу:
h* = arg шт^н- Е^Ь , T )]
с ограничениями на вычислительный бюджет и частичное обучение (Алгоритм 1). Ключевая гипотеза заключается в том, что динамика изменения L на ранних этапах содержит информацию для прогнозирования конечного качества, что позволяет избегать полного обучения моделей с бесперспективными наборами гиперпараметров.
Алгоритм 1 Двухэтапный выбор гиперпараметров с раширенным признаковым простран ством ____________________________________________________________________________ Require:
H — пространство гиперпараметров
I — число кандидатов на итерацию
-
п — число эпох частичного обучения
L — функция потерь
-
u — функция вычисления признаков
Ensure:
-
h* — оптимальные гиперпараметры
1: Инициализация: 2: Генерировать начальную популяцию {hj}^1 ~ Po(h) 3: for i = 1.. .N do 4: Обучать модель c hj в течение п эпох, получить Li 5: Вычислить признаки Ui = u(hj,Lj) 6: end for 7: Построить ТГЕ p(h, u|L) 8: Основной цикл: 9: while критерий останова не достигнут do 10: Отбор кандидатов: 11: Выбрать I точек {hj}j=1 из argmaXhp(h, u|L) 12: Частичное обучение: 13: for j = 1 . ..Z do 14: Обучить модель hj на п эпох 15: Обновить Lj. ВЫЧ11 СЛИТЬ uj 16: end for 17: Обновление модели: 18: Пересчитать p(h, u|L) на основе расширенного пространства признаков 19: Выбрать h* = argminh ^2[L|h, u]
x
20: end while
21: Возврат: h*
3.2. Анализ предложенного метода
Таким образом, предложенный алгоритм подбора гиперпараметров, легко встраивается в существующие методы путем повторного вызова метода ранжирования объектов, например, ТРЕ. Это делает его гибким с точки зрения использования.
Рассмотрим задачу байесовской оптимизации гиперпараметров модели, где целью является нахождение значений h G H, минимизирующей итоговую функцию потерь L( h ). Предположим, что к каждому набору гиперпараметров h могут быть сопоставлены два типа признаков: znajve(h ) — базовые признаки (например, сами гиперпараметры) и
Пусть на базе этих признаков строятся ядерные оценки плотности pu p(h ) и pdo^ vn(— ) — оценки плотности элементов с низким (top-25%) и высоким (bottom-75%) значением функции потерь соответственно, а за функцию ранжирования примем EI (1).
Обозначим:
„naivc( h ) hybrid 7, Ч
Rn;iiV(,(h ) = ^-фф, Rhvl )ri(l(— ) = „V^-), , ,
„0 7Л,Г— pdoWm (-)
где плотности вычислены по соответствующим признакам.
Теорема (об асимптотическом неухудшении ранжирования при расширении статистики)
Пусть для — G H да;ты Т1 = znaive ( — ) — базовые признака и Т2 = ( znaive ( — ), gh ) — расширенные признаки, где gh — результат частичного обучения.
Разобьём множество моделей на два класса:
U = {£(—) в top-25%}, В = {£(—) в bottom-75%}.
Определим для i G {naive, hybrid}
Ri ( — )
„S( — ) j,dL(—),
где плотности pUp и pdOwn оцениваются по Ti с помощью KDE.
Если М ^ ж и выполняются стандартные условия консистентности KDE (М ^ от и стандартных условиях [28] на гладкость, бм ^ 0 и MhM ^ отф то для любых — 1 , — 2 G H с L( — 1 ) < L( — 2 ):
p(^ hybrid ( — 1 ) > R hybrid ( — 2 ) I L( — 1 ) < £( — 2)) % p(R naive ( — 1 ) > R naive ( — 2 ) | M— 1 ) < L( — 2)) •
Доказательство:
При выполнении стандартных условий консистентности KDE:
p®(*) --^ p ( ^ I U ), p dOwn W --> P(t I В).
Следовательно, Ri ^ R*.
По построению T1 проекция T2: T1 = 7r(T2), поэтому из неравенства обработки информации [27]:
I (L; T2) % I (L; T1).
Если записать взаимную информацию через энтропии:
I(L; Ti) = В (L) - П(L | Ti) ^ П(L | T 2 ) ф П(L | T 1 ).
Значит, T2 даёт не меньшую апостериорную определённость о L, чем T1.
Рассмотрим задачу попарной классификации: для фиксированной пары — 1 , — 2 определим бинарную метку:
у
= (1, L(
—
1
)
I 0 , иначе.
Байесовский классификатор по T'i минимизирует риск p(Y = Y ) и основан на тесте отношения правдоподобий ^Z0|^.
Так как T2 информативнее (Н(L | T2) ф П(L | T1)), минимальный риск при T2 не больше, чем при T1 [27]. Значит, вероятность правильного решения p(Y = Y) пр и T2 не меньше.
Наконец, при М ^ от KDE-оценки сходятся к истинным плотностям. Поэтому процедура, использующая Ri, реализует оптимальный байесовский классификатор на Ti. Следовательно, в пределе вероятность корректного ранжирования, реализуемая практической процедурой на основе T2 (то есть Rhybrid), не меньше, чем у процедуры на основе T1 (то есть Rnaivc)' Это формально даёт требуемое неравенство:
p(Rhybrid( h l ) > Rhybrid( h 2 ) | T( H 1 ) < T( h 2 )) > p(Rnaivc( h i ) > Rnaivc( h 2 ) | T( H 1 ) < T( h 2 )).
Замечание (о чувствительности к выбору признаков): Эффективность метода существенно зависит от информативности используемых признаков и. На практике рекомендуется включать в U не только значения функции потерь, но и производные показатели, например, скорость уменьшения функции потерь, совместную информацию между входом и выходом и т.д.
4. Вычислительный эксперимент
В данном разделе представлены результаты экспериментальной оценки предложенного алгоритма подбора гиперпараметров нейронных сетей - вариационного и обычного автокодировщиков. Эксперименты проводились на стандартных наборах данных CIFAR и Fashion-MNIST и заключались в сравнении предложенного метода с базовым алгоритмом ТРЕ.
4.1. Наборы данных
Для проверки эффективности предложенного метода использовалось два набора данных CIFAR-10 [9] и Fashion-MNIST [10]. CIFAR-10 — набор данных для задач классификации изображений, содержащий 60 000 цветных изображений размером 32 х 32 пикселей, разделённых на 10 классов. Набор включает 50 000 обучающих и 10 000 тестовых изображений. Fashion-MNIST — набор данных, содержащий изображения одежды и аксессуаров размером 28 х 28 пикселей в градациях серого. Набор включает 60 000 обучающих и 10 000 тестовых примеров, разделённых на 10 классов.
Оба набора данных широко используются для оценки алгоритмов машинного обучения, что позволяет сравнивать предложенный метод с существующими подходами.
4.2. Параметры автокодировщика и дополнительные признаки
В процессе оптимизации рассматривались следующие гиперпараметры: количество слоев в кодировщике и декодировщике, размерность скрытого пространства, характеристики свёрточных слоев, включая размеры отступов, размеры ядер и шагов свёртки , а также статистические показатели количества фильтров в свёрточных слоях — максимальное, минимальное и среднее значения, наряду со средним изменением. Дополнительно учитывались общее число весов модели и степень сжатия данных.
Для формирования расширенных признаков zhyb rid (ж), извлекаемых в ходе начальных этапов обучения, использовались различные признаки динамики обучения: значения функции потерь, а для вариационных автокодировщиков дополнительно KL-дивергенция. Также вычислялись показатели совместной информации и канонической корреляции между входными данными, выходными данными и скрытыми представлениями. Дополнительно анализировались квантильные распределения весовых коэффициентов кодировщика и декодировщика вместе с коэффициентами эксцесса для этих распределений.
Замечание: Для минимизации затрат на вычисления дополнительных признаков можно использовать только функции потерь на k-ой итерации и динамику их изменения, если к > 1.
4.3. Протокол эксперимента
Эксперимент проводился следующим образом:
Инициализация: На каждой итерации выбиралась случайная подвыборка из 5 элементов обучающего множества и обучалась на 100 эпохах. Рассчитывалось среднее значение функции потерь на получившихся элементах.
Обучение ТРЕ: По этой подвыборке вычислялись целевые значения для обучения ядер-ной оценки плотности (ТРЕ). Отбор кандидатов:
• Классический метод: выбирались кандидаты на основе исходного ранжирования ТРЕ.
• Предложенный метод: изначально отбиралось к кандидатов при помощи ранжированием базовым ТРЕ, затем эти кандидаты дообучались на одной эпохе. После чего на основе их функций потерь и дополнительных признаков проводился финальный отбор через ранжирование ТРЕ.
4.4. Результаты
Обновление обучающего набора данных: Выбранный кандидат обучался на 100 эпохах и добавлялся в множество для обучения. После чего перерассчитывалось среднее значение функции потерь на размеченных элементах. Критерий качества: Динамика средней функции потерь отслеживалась в течение N итераций эксперимента. Кроме того, по окончании эксперимента рассчитывалась средняя площадь под графиком средней функции потерь для базового алгоритма ( Snaive) и предложенного (Shybrid)- Разница между площадями от первой до 150 итерации алгоритма, а также число шагов, необходимое для достижения минимального значения функции потерь базового алгоритма, также использовались как критерий качества. Алгоритмы для сравнения: В эксперименте сравнивались базовый алгоритм ТРЕ, предложенный метод Proposed(Z), где I — число кандидатов на первом этапе, и метод Full, который заранее имел доступ ко всем базовым и рассчитанным статистикам. Стоит отметить, что алгоритм Full является исключительно теоретическим и не может быть использован на практике, а в работе представлен исключительно для сравнения.
Эксперимент повторялся 256 раз, а результат для каждого номера итерации усреднялся для получения статистической значимости результатов.
Для демонстрации эффективности предложенного алгоритма были построены графики (рис. 1) со средним значением функции потерь в зависимости от числа размеченных элементов. Использование среднего значения функции потерь, а не лучшего предсказанного на итерации, вызвано тем, что графики становятся более гладкими и интерпретируемыми. Резкое падение функции потерь вызвано тем, что инициализация первых элементов случайна. Поскольку эксперимент проводился на ограниченном наборе гиперпараметров, то рост среднего значения функции потерь в размеченных данных вызван тем, что после выбора лучших кандидатов алгоритмы выбирали из оставшихся, на которых ошибка была выше.
Результаты эксперимента подтвердили эффективность предложенного метода. На обоих наборах данных среднее значение функции потерь размеченных моделей при использовании предложенного алгоритма оказалось ниже, чем при базовом ТРЕ-подходе.
Как видно из таблиц 1 и 2, предложенный алгоритм демонстрирует статистически значимое улучшение по сравнению с базовым методом. На рисунке 1 графики динамики изменения среднего значения функции потерь на размеченных данных также показывают, что предложенный метод быстрее сходится к меньшим значениям функции потерь.
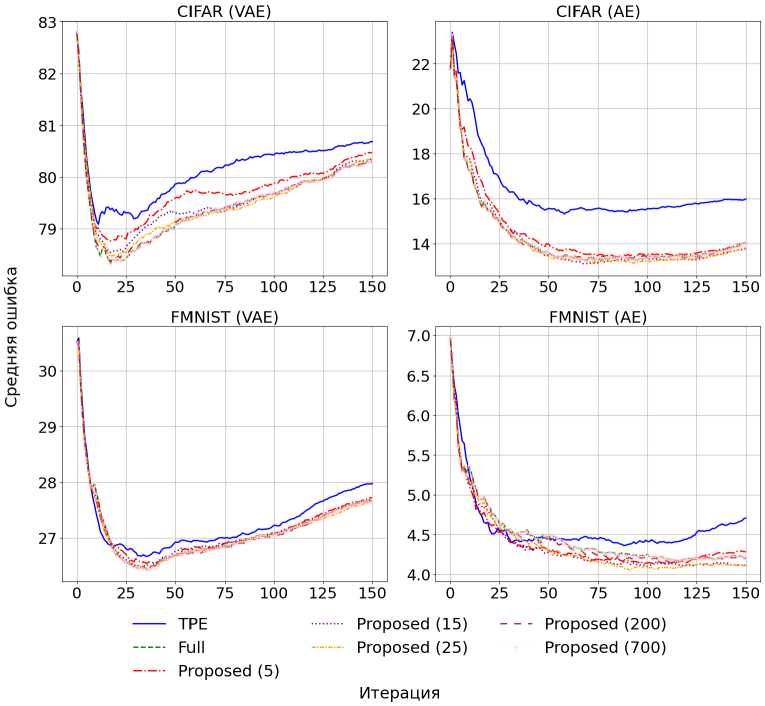
Рис. 1. График среднего значения функции потерь на наборе данных из отобранных алгоритмом и обученных моделей
Таблица!
Разница площадей под графиками среднего значения функции потерь размеченной выборки от числа итераций. Рассмотрено на числе итераций, равным 150
|
Набор данных |
Модель |
^T P E | — I S fuII | |
^TPE | — lSprOposed(5)1 |
^TPE | — lSprOposed(15)1 |
|
Fashion-MNIST |
AE |
24.10 ± 8.13 |
31.42 ± 7.58 |
41.25 ± 7.53 |
|
Fashion-MNIST |
VAE |
29.28 ± 6.91 |
19.16 ± 7.03 |
25.46 ± 7.02 |
|
CIFAR-10 |
AE |
314.59 ± 21.97 |
277.53 ± 19.35 |
325.72 ± 20.72 |
|
CIFAR-10 |
VAE |
101.19 ± 10.65 |
50.42 ± 10.88 |
86.38 ± 10.35 |
Т а б л и ц а 2
Число шагов для достижения лучшего значения функции потерь базового метода с процентным уменьшением относительно ТРЕ. SBTB — это Steps Best То Baseline, число шагов для достижения лучшего результата базового алгоритма
|
Набор данных |
Модель |
SBB TPE |
SBB Full |
SBB Proposed(5) |
SBB Proposed(15) |
|
|
Fashion-MNIST |
AE |
88 |
61 |
(-30%) |
36 (-59%) |
34 (-61%) |
|
Fashion-MNIST |
VAE |
35 |
22 |
(-37%) |
26 (-25%) |
23 (-34%) |
|
CIFAR-10 |
AE |
58 |
22 |
(-62%) |
25 (-57%) |
23 (-60%) |
|
CIFAR-10 |
VAE |
11 |
8 ( |
-27%) |
10 (-9%) |
9 (-18%) |
5. Заключение
В данной работе представлен новый алгоритм байесовского подбора гиперпараметров авторегрессионных сетей, основанный на двухэтапной процедуре отбора. Теоретическая значимость исследования заключается в разработке формальной постановки задачи, доказательстве соответствующей теоремы об условиях эффективности метода, а также введении нового класса алгоритмов, объединяющих байесовскую оптимизацию с ранним прогнозированием качества моделей. С практической точки зрения предложенный метод демонстрирует существенные преимущества, показывая сокращение вычислительных затрат до 60% по сравнению с базовыми подходами в экспериментах на стандартных наборах данных.
Перспективные направления дальнейших исследований включают разработку оптимальных стратегий выбора признаков для различных классов моделей, создание адаптивных схем определения числа эпох частичного обучения, применение метода для архитектурного поиска (NAS) и его интеграцию с методами метаобучения для эффективного переноса знаний между задачами.
Следует отметить, что основное ограничение метода связано с необходимостью тщательного подбора характеристик частичного обучения, таких как число эпох п и состав признаков й, для каждой новой задачи. Однако экспериментальные результаты подтверждают, что на практике для настройки этих гиперпараметров достаточно небольшого числа пробных запусков.


