Выбор оптимальных режимных параметров в областях взаимного поглощения линий равного значения показателя качества изделий

Процессы термообработки композиционных изделий протекают в условиях действия большого числа случайных факторов, поэтому и показатель качества изделий носит случайный характер.1

Для процесса термообработки изделий присуща противоречивость показателей качества, например, стоимость и точность, прочность изделий и однородность прочности. Если в качестве показателя эффективности принять производительность, то можно упустить вопросы, связанные с качеством изделий, экономией цемента и энергии, сохранностью оборудования и т. п.

Таким образом, при исследовании сложных процессов мы имеем дело с несколькими частными показателями, которые оценивают их работу, являются случайными функциями и могут быть противоречивы с точки зрения управления системой.

При определении эффективности управления в пространстве параметров настройки возможны следующие частные случаи:

• 1.    Значения управляющих параметров и показателя качества изделий функционально связаны. В этом случае эффективность управления строится в соответствии с требованиями, предъявляемыми к выходной переменой – прочности изделий. Вы-

• ходная характеристика системы классифицируется по определенным классам, сортам и т. д. или по степени совмещенности линий равных значений целевой функции. Каждому сорту или классу может соответствовать определенная оценка по прочности изделий или отпускная цена. В этом случае, как правило, решается задача максимизации нахождения параметров в заданном классе (например, максимизация вероятности получения изделий заданной прочности при минимальном расходе тепловой энергии на термообработку).2

• 2.    Между управляющими параметрами и прочностью изделий имеет место вероятностная связь. При этом предполагается, что при каждом значении управляющего параметра U известно распределение показателя качества изделий R_k и заданы интервалы значений этого показателя, соответствующие некоторым установленным классам или, например, трем маркам изделий после их термообработки.

• 3.    Как отмечалось выше, при исследовании данного сложного процесса приходится иметь дело с несколькими частными критериями качества. Известно, что задача управления процессом решается намного проще, если рассматривается единственный обобщенный показатель эффективности,

который является количественной оценкой всех требований, предъявляемых к результату функционирования процесса.

Обобщенный показатель учитывает многие требования, предъявляемые к результату функционирования подсистемы термообработки в условиях неопределенности, а именно стоимостные показатели, качество и количество изделий и т. д. Можно поэтому считать, что обобщенный показатель имеет единственный экстремум в некоторой рабочей области пространства параметров настройки, т. е. эффективность управления унимодальна. Изделия равной прочности могут быть получены при различных значениях управляющих параметров, т. е. при различных режимах термообработки. Однако режимы оказываются неоднозначными с точки зрения энергозатрат при получении одинаковой прочности изделий. Результаты исследований позволяют предложить ряд функциональных зависимостей, которые полезно использовать при построении эффективности управления по экспериментальным данным. Точнее, речь идет о выборе структуры уравнения регрессии обобщенного показателя эффективности по параметрам технологического процесса. Процедура выбора регрессии обобщенного показателя эффективности не может быть выполнена чисто формальным путем математическими методами, а опирается на имеющийся опыт термообработки изделий, знание технологических особенностей объекта управления и анализ его статистических свойств. Естественно, что данные о процессе термообработки композиционных изделий охватывают почти квазиоптимальную область, в которой не проявляются полностью характерные свойства целевой функции - ее резкий спад, переход в область отрицательных значений и т. п. Применение же активных методов на реально действующем объекте обычно невыполнимо из-за необходимости пробных воздействий большой величины, что может привести к браку изделий. Эти положения еще раз подтверждают целесообразность и полезность неформальных подходов при формировании целевой функции - эффективности управления.

На основании выполненных исследований и результатов решения конкретной задачи в данной работе определено, что эта функция является дискретной. Она предусматривает разбиение допуска (или в целом области качества D ) на непересе-кающиеся подмножества значений параметров и ставит в соответствие каждому подмножеству (области взаимного поглощения линий равного значения целевой функции) определенное значение показателя качества изделий, или эффективности управления. Это облегчает классификацию изделий по качеству при минимальных энергозатратах на термообработку. Метод разбиения на непересе-кающиеся подмножества представлен на рис. 1.

Опыт изучения технологических процессов термообработки композиционных изделий показывает, что на практике чаще всего используются дискретные целевые функции. Однако устанавли-мая действующими на предприятиях нормами классификация выходного продукта носит слишком общий характер. Часто заданы лишь предельные значения прочности изделий, определяющие

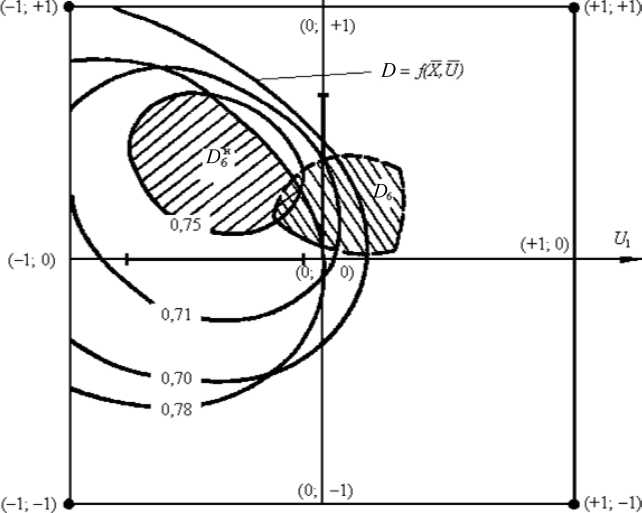
Рис. 1. Область взаимопоглощения изолиний критерия D = f ( X,U в j -х ситуациях «внешней среды»

годность изделия, иногда ограничения носят односторонний характер.

Детерминированная целевая функция обычно имеет место при низком уровне помех в подсистемах смесеприготовления и термообработки и при совпадении управляющих параметров и показателя качества изделий. В зависимости от полученной характеристики результата функционирования подсистемы термообработки композиционные изделия разделены на K ( к = 1, ..., 5 ) сортов или классов по прочности и каждому из них ставятся в соответствие определенные области взаимного поглощения, в которых управляющие параметры инвариантны к соотношению компонент векторов контролируемых возмущений. Тогда множество значений управляющих параметров в подсистеме термообработки можно разделить на подмножества по числу областей взаимного поглощения (сортов изделий) и определить тем самым детерминированную дискретную целевую функцию.

Как показали исследования, результаты которых представлены в данной работе, подсистема термообработки композиционных изделий в условиях неопределенности является стохастическим объектом управления, т. е. она характеризуется неоднозначностью отклика на одни и те же входные и управляющие воздействия. Поэтому все показатели качества функционирования подсистемы термообработки являются случайными функциями ее параметров.

Вид полученных гиперповерхностей при различных сочетаниях параметров подсистемы смесе-приготовления на основных уровнях говорит о том, что процесс термообработки можно вести на различных режимах, выбор одного из них определяется минимумом энергозатрат при получении максимальной прочности при равных условиях со стороны параметров подсистемы сырьевого передела.

Построение многомерной дискретной целевой функции можно осуществить с помощью алго- ритмов назначения допусков на параметры подсистемы термообработки при фиксированных текущих параметрах подсистемы смесеприготов-ления. Как показано в данной работе, показатель F = F(x1, ..., xn; u1, u2, u3), оценивающий качество функционирования системы управления, имеет s градаций сортов изделий, т. е.

0 <  F ( x 1 , ..., x n ; u 1 , u 2 , u з ) <  F 1 - I сорт;

..........                           (1)

F_s _ 1 <  F ( x 1 , ..., x n ; u 1 , u 2 , u 3 ) < F₅ - 5 -й сорт.

Каждому сорту изделий будет соответствовать область Dk (к = 1, ..., 5) допустимых вариаций параметров. Аппроксимируя каждую из областей Dk (к = 1, ..., 5) брусом, получим, используя его координаты, многомерную функцию цели. Выбор дополнительного критерия при аппроксимации области Dk (к = 1, ..., 5) брусом Вк опре- деляется исходя из вероятности получения изделий данного сорта.

Многомерную дискретную функцию цели можно записать в виде b1, если x j < xj < x2 j; u1 i < ui < u2i;

Ф ( X , U ) = ^                 ........ (2)

b5, если x5j < xj < x2j.; u5 < ui. < u5, где bk – оценка изделия k-го сорта (например, прочности после термообработки).

Взаимное положение областей Dk различно для частных критериев y4 и y 28 , как это показано в результате проведенных исследований (см. рис. 1), и может определяться качественными характеристиками сырья даже для каждой из областей в отдельности. На рис. 2 представлены случаи построения многомерной дискретной функции цели. В случае а низший сорт включает в себя высший, и при настройке САУ можно определить вероятность по- u232 u222 1 u22

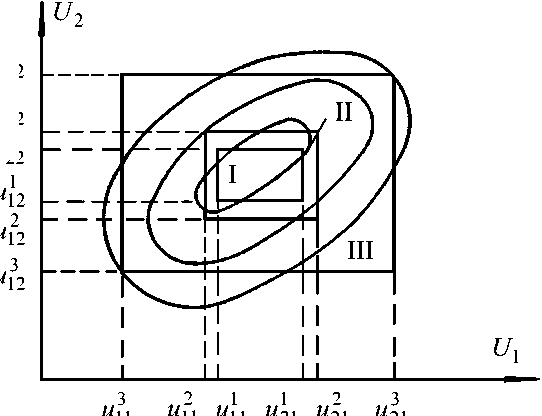
а)

Рис. 2. Виды многомерной дискретной функции качества: а – низший сорт включает в себя высший; б – с учетом ограничений по участкам

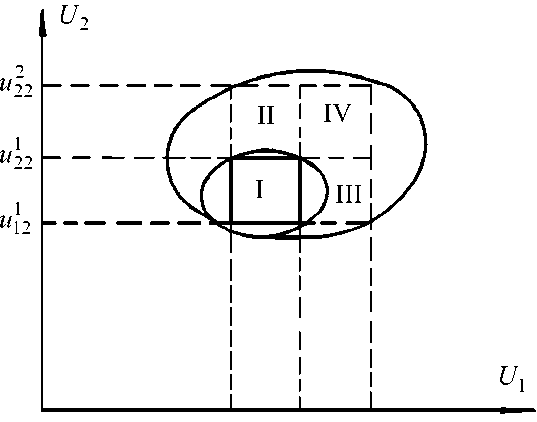
б)

лучения изделий k -го сорта. В случае б различают четыре участка, которые определяют ограничения на параметры u i ( i = 1, ..., n ) при управлении или настройке САУ на определенный режим работы. Участок I определяет ограничения на параметры, при которых выпускается продукт I сорта. Участки II–IV определяют ограничения на параметры u_i ( i = 1, ..., n ) , при которых выпускается продукт II сорта. Однако, исходя из условия, что коэффициент вариации прочности бетона допускается до 12 %, можно отдать предпочтение участку, в котором обеспечивается минимум расхода тепла на термообработку. Например, при ограничениях на параметры u_i согласно участкам II или III лучше показатели качества изделий II сорта из-за того, что параметры u 1 и u 2 находятся в допуске, соответствующем I сорту. Возможно, предпочтительнее участок IV, например, из-за меньшего расхода цемента. Все эти факторы учитываются при формировании оценки b_k и способствуют принятию оптимального решения.

В большинстве практических случаев нахождение обобщенных показателей не может быть выполнено формальными математическими методами и представляет собой творческую задачу выбора наилучшей характеристики результата функционирования технологического процесса. Задача многокритериальной оптимизации на практике встречается весьма часто, поэтому ее решению в последнее время уделяется много внимания. Например, разработана теория антагонистических игр, в которой успешно работает доказанный фонНейманом принцип «минимакса». В случае неантагонистических игр применим принцип согласованного оптимума В. Парето, который предполагает, что улучшение одного критерия не допускается за счет ухудшения другого, т. е. использование этого принципа является наилучшим с точки зрения всех критериев.

Исследования показали, что при стремлении в равной степени удовлетворить всем показателям существует оптимальная точка, определяемая решением уравнения

D Fl D X = 0, (3)

где F – вектор, составленный из критериев F_i ( i = 1, ..., m ) , а D/D X - якобиан векторного преобразования.

Построение и решение уравнения (3) часто затруднительно из-за неопределенности критериев и различного их физического содержания.

Решение многокритериальной задачи упрощается, если каждый из частных показателей качества функционирования системы может изменяться лишь в некотором диапазоне своих значений. В этом случае для построения обобщенной целевой функции могут быть использованы методы назначения допусков.

В данной работе рассматривается задача построения обобщенного показателя качества функционирования подсистемы термообработки композиционных изделий в условиях неопределенно- 4      28

Рассмотрим оба случая:

• 1.    Результат функционирования подсистемы термообработки оценивается m критериями каче- 4        28

• 2.    Результат функционирования подсистемы термообработки оценивается m критериями качества. По каждому из критериев различаются k сор-

• тов (к = 1, ..., 5), как это показано в результате проведенных исследований на рис. 2. Задача сводится к определению в пространстве параметров областей Dk (к = 1, ..., 5), соответствующих каждому k-му сорту, т. е. m

ства, т. е. прочностью изделий y и y или прочностью изделий и однородностью прочности. По каждому из критериев в пространстве R n определена односвязная область допустимых вариаций параметров Di (i = 1, ..., m) так, что для всех точек множества Di соответствующие оценки качества изделий не выходят за пределы ГОСТа. Задача сво- m дится к определению D = Q Di . Считаем, что об-i=1

ласть D существует, если система уравнений

Fi (x1, ..., xn , u1,... , um )   Fi i = 1, ..., m, в = 1,2

совместна и ее решение не вырождается в точку.

Для управления процессом термообработки с целью обеспечения заданных показателей качества y 4 и y 28 необходимо назначить допуски на настроечные параметры u так, чтобы выполнялись все критерии.

Решив задачу построения вложенного бруса, с помощью его вершин определим допуски на параметры u_i , т. е. u 1 _i и u 2 _i , в пределах которых обеспечиваются требуемые значения всех критериев качества. Иллюстрация рассмотренной задачи построения многокритериальной дискретной целевой функции представлена на рис. 2.

D k = Q D ki .                             (5)

к = 1

Для определения допусков на параметры u_i ( i = 1, ..., n ) , в пределах которых подсистема термообработки работает с требуемым показателем качества y 4 и y 28 , т. е.

F 1k <  F ( X , U ) < F , ik ,                     (6)

проведем аппроксимацию области D_k брусом B ₀ или B_v , или B_n . После решения S задач дискретная обобщенная функция цели запишется как выражение (2).

Номинал, доставляющий максимум критерию оптимальности Q , будем называть оптимальным номиналом и обозначать u_n 0 .

Основываясь на теоретических положениях В.В. Здора, рассмотрим подсистему термообработки, математическая модель которой имеет вид (7)

y = f ( 0 , X , U ) ,                          (7)

где y – показатель качества изделий; X – k -вектор контролируемых параметров; U – l -вектор управления. Векторы 0 , X и U удовлетворяют ограничениям 0 е 0 ; X е X ; U е U , где 0 , X , U ^ˆ – заданные ограниченные множества. Случайные отклонения значений компонент 0 , X , U приводят к неопределенности показателя качества изделий y . Учитывая это обстоятельство, на показатель качества y устанавливаем ограничения [ у 1 , У 2 ] , так как реализация всей партии изделий с одним и тем же значением показателя качества их невозможна. Область допустимых значений показателя качества, отображенная в пространстве компонент 0 , X , U , определяет множество их допустимых отклонений

D j = { 0 , X , U е R " ^{+ 1 + к}/ у ! <  f ( 0 , X , О ) <  у ₂ } . (8)

Математическое решение проблемы управления качеством композиционных изделий состоит в том, чтобы определить область D_j и выбрать принадлежащие ей 0 _н, X _н , U _н, которые с учетом возможных случайных отклонений обеспечивали бы для всей партии изделий лучшие в среднем значения показателя качества. Эту проблему можно записать как задачу стохастического программирования.

На основе предпосылок работ В.В. Здора выделим два уровня параметрического управления: нижний, реализующий параметрическое управле- ние с помощью компонент 0 , X , U , и верхний, определяющий критерий управления в зависимости от полноты информации об изменении показателя качества изделий у. Информация о показателе качества имеется следующая: заданы допустимые пределы изменения показателя качества y1 , y2 ; построена функция качества ф(h,у), характеризующая изменение качественных оценок изделий в зависимости от изменений значений у; определена плотность распределения показателя качества p(y). На основании этой информации и в зависимости от ее сочетания вырабатывается стратегия управления процессом термообработки и определяется оптимальное задание на управление.

При этом следует различать две ситуации:

• 1.    Функция качества ф ( h , у ) определена на

• 2.    Функция качества определена на нижнем уровне, т. е. определена функция ф ( у , й ) . Тогда

верхнем уровне параметрического управления качеством изделий. Тогда оптимальное задание на управление y0 определяется также на верхнем уровне, а выбор оптимального управления u 0 с учетом погрешности измерения X и отработки U осуществляется из условия обеспечения мак симальной вероятности выполнения у е [у1, у2 ].

выбор оптимального й ⁰ осуществляется по критерию эффективности.

Рассмотрим выбор стратегии на верхнем уровне параметрического управления качеством композиционных изделий.

Заданы только допустимые пределы изменения показателя качества, т. е. функция качества определена в виде

ф ( » , у ) = | 1, если ^{у е[}, ^{у 1 у} 2 ] ;

^{v 1} [ 0, если у й [ у ! , у 2 ] .

Такое управление определим как безусловное, и одна из возможных рекомендаций для выбора оптимального задания заключается в определении

0 = у 1 + у ^ 2 y 2

где y 0 – оптимальное задание на управление. Выбор управления осуществляется по модели у0 = f (0, JX, t/).                            (11)

Учитывая, что в результате проведенных экспериментов на объекте определена плотность распределения вероятности p(y) и установлены ограни- чения y1 , y2 , то по критерию параметрической надежности y2

p ⁰ ( 1 ⁰ ) = m l ax J P [^ ( у , 1 ) ] dy (12)

y 1

при у 1 <  1 <  у ₂ определим оптимальное задание

У 0 = У p + 1 0 , (13)

где y p – расчетное задание до проведения экспериментов.

Из (11) следует, что настраивая процесс термообработки на оптимальное задание y 0 , мы обеспечиваем получение максимального количества изделий с однородным показателем качества y e [ y 1 , y 2 ] . Принимая во внимание, что функция качества ф ( h , у ) в допуске [ y 1 , у 2 ] построена, то оптимальное задание определим из решения задачи

ф ( h , у 0 ) = extr ( h , y ) . (14)

Введение функции качества ф ( h , y ) дает возможность из множества допустимых управлений, обеспечивающих y e [ y 1 , y 2 ] , выбрать такое, при котором достигается выпуск изделий с однородным показателем качества при минимуме энергозатрат на термообработку.

Используя функцию качества ф ( h , y ) , можно корректировать ограничения [ y 1 , у 2 ] из условия

ф ( h , у р ) = Рф ( h , у ⁰ ) , ⁽¹⁵⁾ где 0 < р <  1; в = 1,2.

Рассмотрим решение задачи автоматической классификации. Из-за чувствительности оптимальных процедур к вариации лежащих в их основе ограничений на практике часто более эффективными оказываются эвристические методы решения проблем классификации и распознавания. Основными преимуществами эвристических процедур являются их работоспособность в ситуациях с максимальной априорной неопределенностью, алгоритмическая простота, наглядность интерпретации полученных результатов при максимально возможной их точности. Большинство имеющихся методов недостаточно полно удовлетворяют перечисленным требованиям.

В данной работе предлагается новый подход к решению задачи автоматической классификации и распознавания образов. Идея, лежащая в его основе, базируется на принципе взаимного поглощения номиналов, расположенных в гиперпараллелепипедах, аппроксимирующих гиперповерхности отклика с плоскостями параллельными координатным осям настроечных параметров [1–3]: группу составляют только те номиналы, которые попадают в область взаимного поглощения с учетом их допуска.

В зависимости от характера исследования формальные процедуры могут быть применены либо для группировки объектов, либо для выделения классов идентичных условий (наблюдения по набору параметров объекта).

Рассматриваемые объекты имеют n векторов, координатами которых являются номинальные значения параметров состояния при n различных условиях Хн ={хн(1), хн(2), ..., хн(N)}, i = 1, n . Мера близости между этими векторами задана метрикой d (хн, хн), i, j = 1, n в N-мерном пространстве координат. Квадратная матрица D ={d (хн, хн)}, i, j = 1, n, определяет совокупность всех возможных парных связей на Xн ={хн}, i = 1, n . Необходимо разбить Xн на K классов Cs, s = 1, k. В общем случае их число может быть неизвестным. Кроме того, не обязательным является условие непересекаемости классов, т. е. Cs П Ct *0 , s, t = 1, k .

Для каждого вектора с вершиной в x_i н проведем радиусом р i гиперсферу Z i , которую аппроксимируем описанным или вписанным брусом B_i . Векторы Х н , t * i , попавшие внутрь гиперпараллелепипеда B_i , будем считать поглощенными x_i н , а гиперпараллелепипед B_i назовем областью поглощения. Введем следующие понятия.

Определение 1. Областью взаимного поглощения D_i назовем пересечение гиперпараллелепипедов B_i при условии, что центры x_i н этих гиперпараллелепипедов являются номиналами параметров и принадлежат указанному пересечению, т. е. D i = J В . ^ х н U B i . qq

Определение 2. Центры x_i н гиперпараллелепипедов B_i , образующих область взаимного поглощения D_i , назовем классом С .

Классификация заключается в поиске K областей взаимного поглощения D_s , s = 1, k , и соответствующих им классов C_s , s = 1, k . В общем случае C_s П C_t *0 , s , t = 1, k , s * t .

Задание решающего правила в явном виде требует определения аналитического выражения для радиуса гиперсферы рi. Одним из способов задания радиусов рi гиперсфер поглощения является выбор постоянного радиуса для всех гиперсфер, т. е. рi = р , i = 1, n . Это сводит задачу классификации к известным методам, основанным на задании жесткого порога дискриминации, в соответствии с которым не рассматриваются все меры близости, меньшие порога, как недопускающие объединение в классы. В этом случае принцип взаимного поглощения теряет смысл, так как xiн , поглотивший xнj , всегда оказывается поглощенным объектом xнj . Именно различная степень поглощения объектами друг друга определяет гибкость процедуры классификации, т. е. появляется возможность определять области качества управ- ления в допуске ±Axн на выходную координату.

Целесообразным представляется выбор выра- жения

Р i

в виде Pi = Рi (d (хн, xн)), i, j = 1, n, i * j. В частности, одним из способов задания этой функции является рi = maxd(хн, xн)-8,                    (16)

где 8 = ±А и н - некоторая постоянная величина, выбираемая из эвристических соображений исследователем, например, допуск на параметр. Выбор 8 позволяет путем ее выравнивания добиваться тех или иных желаемых свойств разбиения на классы.

Радиус р i в нашем случае выбирается равным малой полуоси эллипсоида качества при аппроксимации его квадратом (в n -мерном пространстве – гиперпараллелепипедом).

В случае аппроксимации гиперсферы Zi гипер- параллелепипедом определяются центр гиперпараллелепипеда, длины малой и большой полуосей.

Предлагается способ, основанный на выборе р i как среднего значения элементов i -й строки матрицы близости D по номиналам параметров

1n р 1 = ”[ Е d(xi , xj ). n 1 j=1, j *i

К интерпретации рi, определяемой из (17), можно подойти с других позиций, представляя эту величину как центр тяжести единичных масс, удаленных от нулевой точки отсчета на величину, равную степени близости d (xiH, xн), и располо- женных для xiн на одной прямой. В общем случае, когда массы точек равны mij , уравнение для опре- деления центра тяжести рi имеет вид

n

Е mijd (xiH, xj р i =

n

∑ ^mij

Принимая в (18) m ij = 1, приходим к (17). Выбирая m ij = d ( x i' , x н ) , получаем

n

Е d 2 ( x - , j j = 1, j * i

n

Е d ( x f , x j ) j = 1, j * i

Величины m_ij в (18) можно задавать из априорных соображения либо использовать их как набор настроечных параметров алгоритма классификации.

Проиллюстрируем подход к классификации на основе принципа взаимного поглощения применительно к исследуемому объекту управления.

В двумерном пространстве (см. рис. 1) определены номиналы настроечных параметров u_i н в областях D_i ^н при фиксированных на основных уровнях компонентах вектора параметров сырьевого передела X_i ^н , которые необходимо объединить в группы. С центрами в точках наибольшего удаления номиналов u_i н построены линии равного значения целевой функции и обобщенного критерия с радиусами, равными малым и большим полуосям эллипсоидов качества. Оценим радиусы по формуле (16), т. е. возьмем расстояние до ближайшего к и н объекта u н , i * j , и это расстояние увеличим на величину допуска ±А и н . Аппроксимируем гиперэллипсоиды вписанными прямоугольниками B_i . Области взаимного поглощения D_i получены в соответствии с определением 1. По определению 2 классы составляют номиналы настроечных параметров и н ± А и н . Номиналы и н ± А и н области D 4 поглотили номиналы u_i н областей D 1 , D 2 и D 3 (они попали внутрь области взаимопоглощения D 4 ), но взаимное полное поглощение номиналов произошло только с учетом допусков ±А и н .

Обычные алгоритмы классификации (типа процедур кластерного анализа), выделив класс C ₁ , не объединили бы в группу остальные объекты. Из вышесказанного видно, что принцип взаимного поглощения с учетом допусков дает возможность осуществлять классификацию на группах номиналов параметров или объектов различной компактности. Области взаимного поглощения могут быть пересекающимися.