Выбор оптимальных зазоров в калибре при совмещенной прокатке-прессовании

Одним из глобальных направлений в современной мировой металлургии является создание модульных технологий, которые заключаются в совмещении нескольких металлургических переделов в одном агрегате для производства заданной продукции [1]. Формы совмещения технологических операций весьма многообразны. В области обработки металлов давлением одно из перспективных направлений – совмещение процессов литья, прокатки и прессования. Особенно эффективен процесс СПП для производства длинномерных профилей небольшого поперечного сечения из цветных металлов и сплавов [2]. Однако при реализации процесса СПП сталкиваются с рядом проблем. С одной стороны, при минимальном зазоре увеличивается сила трения на границе контакта подвижных валков и неподвижной матрицы и возрастает абразивный износ инструмента, а с другой – при увеличении зазора возможно появление заусенца, что нарушает стабильность протекания непрерывного процесса СПП, ухудшает качество изделия и снижает выход годного. Поэтому задача выбора оптимального зазора в калибре, с учетом технологических и конструктивных параметров процесса СПП и реологии деформируемого металла, актуальна.

Процесс образования заусенца при СПП аналогичен обратному прессованию с «рубашкой», когда диаметр пресс-шайбы несколько меньше (на 2÷4 мм) диаметра контейнера, и во время прессования отделяется периферийный продольный слой заготовки от основной массы металла, образуя «рубашку». Механизм образования «рубашки» и силовые условия данного

процесса подробно рассмотрены в работе И.Л. Перлина [3]. При этом силовой анализ данного процесса проведен на основе совместного решения приближенных уравнений равновесия и пластичности. Методика расчета давления для закрытой прошивки, которая сопоставима с процессом обратного прессования с «рубашкой», представлена в работе М.В. Сторожева [4], где удельное усилие определено на основе метода баланса работ. Разработанные методики требуют проведения дополнительного анализа и создания новой методики для проведения силового анализа образования заусенца в калибре при СПП с учетом особенностей данного процесса и реологии деформируемого металла.

Методика расчета оптимальных зазоров в калибре для СПП

Процесс образования заусенца в калибре при СПП аналогичен процессу обратного прессования, в котором роль пресс-штемпеля выполняет матрица, а давление прессования создается за счет активных сил трения подвижными валками в калибре. В начальный момент времени заусенец будет образовываться в том случае, если удельное давление прессования будет больше, чем удельное давление при образовании самого заусенца. При определении силовых условий образования заусенца в калибре при СПП вначале рассмотрим данный процесс для цилиндрического пуансона и контейнера и примем, что изменение сил трения подчиняется закону Зибеля, а напряжения трения и напряжения сдвига одинаковы и равны:

т = ^^s , где μ=0,5 – коэффициент трения; σs – сопротивление деформации металла.

При выдавливании (рис. 1) происходит течение металла в кольцевой зазор между торцом пресс-штемпеля 1 и контейнера 3. При этом в образовавшемся заусенце 2 деформации не происходит, и эта часть лишь передвигается под воздействием деформируемого металла 4, непрерывно поступающего в заусенец на уровне 5 торца пресс-штемпеля. Только при коническом пресс-штемпеле деформация будет охватывать также и объем образующегося заусенца. При цилиндрическом пресс-штемпеле металл не обтекает края его торца по направлению к оси пресс-штемпеля, и форма последнего может быть такой, какая представлена на рис. 2. Удельное усилие на пресс-штемпеле, необходимое для образования заусенца, определим методом баланса работ, взяв за основу схему процесса, представленную на рис. 2 . Для какого-то момента процесса цилиндрическая зона 1 диаметром d =2 r и высотой h осаживается пресс-штемпелем, а кольцевая зона 2 с наружным диаметром D =2 R = d +А и той же высотой h подвергается внутреннему давлению, и некоторое количество металла из этой зоны вытесняется вверх в жесткую зону 3 деформированного металла, увеличивая объем последней. Зона 4 в этот момент рассматривается как жесткая. При этом высота деформируемых зон 1 и 2 в течение всего процесса деформирования остается постоянной и равной h .

Малые перемещения пуансона и ₀ будут направлены вниз, а перемещения прошитой части или заусенца u – вверх:

u 0

1 4                          ,

( Rr )² -1

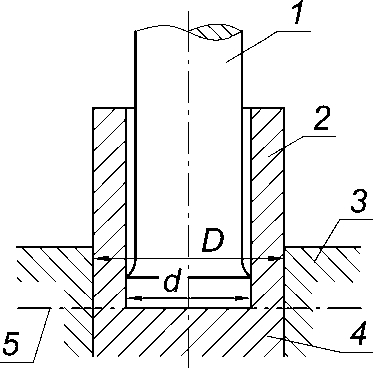
Рис. 1. Процесс образования заусенца при обратном прессовании: 1 – пресс-штемпель; 2 – заусенец; 3 - контейнер; 4 - деформируемый металл;

5 – уровень торца пресс-штемпеля

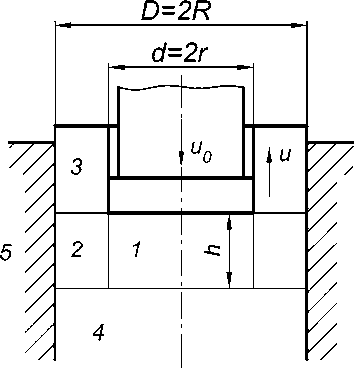
Рис. 2. Схема к расчету силовых условий образования заусенца

Удельное усилие на пресс-штемпеле p_ПР можно представить как сумму:

Р пр = Е P i ,                                                ⁽³⁾

i = 1

где p_i – доли удельного усилия, необходимые для:

• p i - деформирования осадкой зоны 1;

• p 2 - деформации кольцевой зоны 2;

• p 3 = p 1,2 - p 2,5 - преодоления трения по цилиндрической контактной поверхности между зоной 2 и контейнером и осуществления сдвига по цилиндрической поверхности разрыва между зонами 1 и 2;

• p ₄= p 1, _P + p 1, ₄ - преодоления трения между торцом пресс-штемпеля и зоной 1 и сдвига по поверхности разрыва между зонами 1 и 4;

• p ₅= p ₂ , ₃+ p ₂ , ₄ - осуществления сдвига по кольцевым поверхностям разрыва между зоной 2 и зонами 3 и 4;

• p 6 = p ₃ , P + p ₃ , ₅ - преодоления трения по цилиндрической контактной поверхности между зоной 3 и пресс-штемпелем и контейнером.

Далее определяем составляющие p , удельного усилия на пресс-штемпеле. При определении перечисленных составляющих удельного усилия для зон, которые граничат с контейнером 5 (рис. 2), следует учитывать, что контейнер образован подвижными валками. Поэтому на границе контакта зоны 2 и контейнера, где скорость движения валков больше скорости перемещения деформируемого металла, будут действовать активные силы трения (p ₂₅ < 0), а на границе контакта зоны 3 с контейнером, наоборот, скорости истечения заусенца превышают скорости движения валков, поэтому силы трения будут реактивными ( p _{3 5} > 0).

Удельное усилие p 1 при осадке зоны 1 будет равно p 1 =во _$ , где 0-1,1

Деформация кольцевой зоны 2 будет осесимметричной, а деформацию eZ можно принять при малых перемещениях постоянной, тогда:

Из условия постоянства объема получим:

	du t + р + h "0                                  (5)
Тогда:	d ( pu p )     pu =      .                                                         (6) dp     h

Учитывая, что у стенки контейнера при ρ= R перемещение u ρ =0, то после интегрирования

£ z =

u h ^;

^

dup dp ’

e_e =

U p

P

и определения постоянной интегрирования получим:

, = u0L 1 R 2 - P^{2 P} 2 h ⁽ Rr )^{2 -} 1     ^p

Тогда компоненты деформации будут равны:

	du	u 0        1	R 2
е р	= —^ d p u	2 h ( Rr )2 u 0         1	-1» 0 р' 2	(8)
ев	= —р = р u	2 h ( Rr )2 - u	1(1 - р 2 );	(9)
£ Z Z	h	—0 h ( Rr )2 -1	.	(10)

Учитывая, что ( R/p )² > 1, то деформации e _Z, e ₆ будут положительны, а деформация е _р - отрицательна и максимальна по абсолютной величине. Так как интенсивность деформаций ε в ¹

данном случае мало отличается по абсолютной величине главной деформации, то s i = P\s\ .

max

Уравнение баланса работ для данного случая деформирования можно записать в следующем виде:

βσπu ^R   R ²

Р₂лги о = ^a I SidV =    , S 2 ⁰ I (1 + —) pdp,                 (11)

V(Rr)-1rρ где dV = 2n hp d p.

После интегрирования, подстановки пределов и замены радиусов диаметрами окончательно получим:

1 D

p ₂ = βσ_S (0,5+         ₂ ln ).

• 1 - ( d D )²    d

"ГТ                                        .                                                                                                           .           .                                                                                                                    .       .

При нахождении удельного усилия p3 следует принять во внимание, что перемещение верхней границы зоны 2 относительно контейнера равно и, т. е. перемещению зоны 3, а нижняя граница зоны 2 относительно контейнера неподвижна. Так как осевая деформация зоны 2 2 будет изменяться линейно. Поэтому при расчете работ трения можно взять среднее перемещение:

0,5 u =

0,5 u ₀ ( Rr )²-1^.

Тогда уравнение баланса работ для удельного усилия p ₂ , ₅ примет следующий вид:

2                     0,5u p2 5nr и0 = 0,5 всs 2nRh —;—20—.

^,                           (R r) - 1

Откуда

h Dd ^{p 2,5 = βσ S ⋅} d ^⋅ ( Dd )²-1^.

Аналогично находим удельное усилие p 1 ₂, где в качестве среднего перемещения в уравнение баланса работ подставляем полусумму перемещений и и и ₀:

p 1,2 πr ² u 0 =0,5 βσ S 2 πrh 0,5 u 0 (    ¹₂   +1).

( R r ) -1

Откуда

h 1 ^{p 1,2 = βσ S}d ^⋅ 1-( dD )^2.

Далее окончательно получаем:

h 1

p ₃ = p _{1 2} - p _{2 5} = βσ_S ⋅ ^{,     ,} d 1+ dD

.

Расчет удельного усилия p ₄= p 1 _P + p 1 ₄ на преодоление трения между торцом пресс-штемпеля и зоной 1 и сдвига по поверхности разрыва между зонами 1 и 4 представлен в работе [4]:

=+= βσ ⋅ ^d

4      1, P     1,4         S _{6 h}

p ₅= p ₂ , ₃+ p ₂ , ₄ - осуществления сдвига по кольцевым поверхностям разрыва между зоной 2 и зонами 3 и 4;

Сдвиг по кольцевым поверхностям разрыва между зоной 2 и зонами 3 и 4 происходит в результате перемещения и р , которое не является линейной функцией координат. Поэтому необходимо выполнить интегрирование по площадям разрыва. Уравнение баланса работ для двух поверхностей будет следующего вида:

βσ 2 πu  ^R R ²

p ₅ πr ² u ₀ =       ^S ₂ ⁰ ∫

2 h [( R r ) -1] ^∫ _r

-

ρ

^ρ ) ρdρ .

После интегрирования и преобразований получим:

d ( d D )³ -3 d D +2 p, = e<7_s ---,-----------~ .

• ^{5    S}h 6 dD [1-( dD )²]

Уравнение баланса работ для преодоления трения по цилиндрической контактной поверхности между зоной 3 и пресс-штемпелем и контейнером будет следующего вида:

2 ^u p ₆ πru ₀=0,5 βσ_S 2 π ( R + r ) l_PΠ     ⁰₂   .

( R r ) -1

Откуда

2βσ lD p6=p3,P+p3,5=1-SdPΠD , где lP – высота рабочего пояска пресс-штемпеля.

Просуммируем найденные значения составляющих удельного усилия на пресс-штемпеле:

ln( D d )  2 l PП Dhd        dh

РпР ~ P^S [1,5 ++**] • ^ПР S^s     1 - ( d/D ) 2   1 - d/D 1 + d/D 3( d/D )(1 + d/D )

В данном уравнении неизвестна глубина очага деформации под пресс-штемпелем h , которая находится на основании принципа минимума энергии деформации:

h=^=IdL где a =-----— и b =--------------сомножители h/d и d/h последних членов уравнения (24).

¹ + d/D      3⁽ d/D )(1 + d/D )

Тогда hd      dh2

+ ^— 2 ab ^— •

1 + d/D 3( d/D )(1 + d/D )        1 + d/D 3dD

Подставляя найденное значение h в уравнение (24) и учитывая (26), окончательно найдем удельное давление в объеме деформируемого металла при выдавливании заусенца:

Р зс = _R. ₍ d ₎ 2 _[1 5 ₊ ln( D/d ) ₊ 2 1 рп ₊         2        ]

ct _s       D ’ 1 - ( d/D )²    A   (1 + d/D)^3 d/D '

Определим удельное давление при выдавливании заусенца на основе совместного решения приближенных уравнений равновесия и пластичности по методике И.Л. Перлина [3]. Решение данной задачи сведем к определению удельного давления при прессовании с обратным истечением трубы или «стакана» на пресс-штемпель. В рассматриваемом процессе в соответствии со схемой, приведенной на рис. 3, общая сила прессования может быть представлена в виде суммы следующих сил:

Р пр = R m - Т 1,2 + 7 2,3 - T 34 + T ₅ ,6 + Т б,7 + T 8,9 ,                      (28)

где R_M – сила, необходимая для осуществления основной деформации без учета сил трения;

T 1,2 - сила для п реодоления трения на участке 1-2 боковой поверхности контейнера;

T_{2 3}+T 5 6 - сила для преодоления трения на участке контейнера 2-3 и на рабочем участке ^,                 '

пресс-штемпеля -^,_

• T ₃ , ₄ - сила для преодоления трения на участке контейнера 3-4, соответствующем высоте пластической зоны h_n3 ;

• T 6,7 – сила для преодоления трения на торцовой поверхности пресс-штемпеля;

• T 8,9 – сила для преодоления трения по дну контейнера.

Силы T],2 и T3,4 будут отрицательными, т.к. на границе контакта с контейнером, который образован подвижными валками, в начальный момент образования заусенца будут действовать активные силы трения. Силу T1 2 в расчет можно не принимать, т. к. давление на внутрен-, нюю поверхность трубы отсутствует, а силы, вызываемые упругими деформациями трубы, несоизмеримо малы по сравнению со всеми прочими силами, действующими на прессуемый металл.

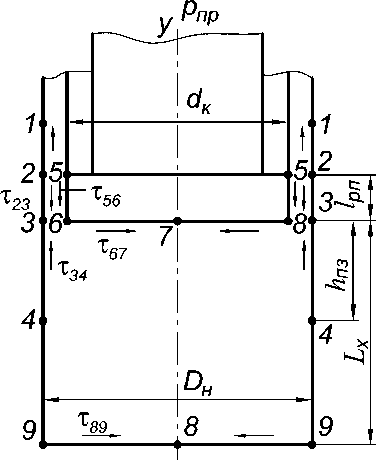
Рис. 3. Схема сил контактного трения, действующих на прессуемый металл при обратном истечении трубы на пресс-штемпель

Силу R M можно определить исходя из следующих соображений: при отсутствии контакт -ного трения течение металла в пластической зоне в рассматриваемом процессе аналогично процессу обратного истечения круглого сплошного профиля через плоскую матрицу, кроме направления течения относительно оси симметрии Y-Y . В рассматриваемом процессе металл течет от этой оси к периферии, тогда как при прессовании круглого сплошного профиля – от периферии к оси. Такое изменение направления течения при отсутствии контактного трения не может повлиять на величину искомой силы, поэтому для ее определения может быть применена формула , в которой следует принять а ПР ~п/2:

F H ^ S ln ^ ЗС

R^M = cos² a J 2 = ² F H ^ S ln ^ ЗС ^{,                          (29)}

где Х зс

F

H

F

ЗС

F

FH

F -F

FH FПР

– вытяжка при выдавливании заусенца;

FH

= ^{n D}H _и f

4 ^ПР

nd 2К

К

- площади поперечного сечения контейнера и пресс-штемпеля со-

ответственно.

Сумма сил T ₂ , ₃+ T ₅ ,6 на участках 2-3 и 5-6 можно рассматривать, как поверхности калибрующего пояска длиной l ПР :

^T 2,3 ^{+ T} 5,6   ^{П ( D}H ^{+ d}K )M s ^ s X 3c l pn

где Ц _s □ 0,5 - коэффициент трения, которое подчиняется закону Зибеля, принимается для всех зон равным максимальному значению.

Скорость скольжения металла по контейнеру на окружности, определяемой точкой 3, равна vМ=λЗС vПР (где vПР – скорость движения пресс-штемпеля). Скорость скольжения металла по – 417 – контейнеру на окружности, определяемой точкой 4, находящейся на границе упругой и пластической зон, можно считать равной нулю. Среднюю скорость скольжения по участку 3-4 можно считать равной λЗС vПР/2. Отсюда, имея в виду равенство мощностей активных и реактивных сил, определяем силу T3,4 по следующей формуле:

^{где h}n3

D H +dK

2 '

—

^Т 3,4    4 ^DH ^U S^/ЗС'ЧЗЗ ,

– высота пластической зоны.

Сила T6 7 определяется на основании того же положения равенства мощностей соответ, ствующих активных и реактивных сил. Учитывая, что средняя скорость скольжения по торцовой поверхности пресс-штемпеля может быть определена по формуле

V cp ( L x ) = v-^ ,                                      (32)

6LX где DX и LX - текущие высота деформируемого металла до дна контейнера и диаметр контакт -ной поверхности, а также, что максимальное сдвигающее напряжение металла в его состоянии на контактной поверхности с пресс-шайбой и коэффициент трения не могут сколько-нибудь заметно отличаться от таких же параметров на боковой поверхности контейнера, применяя уравнение мощностей, определяем силу T6,7:

T67 = -(.l ^S.

,48

Силу T _8,9 определяем на основе тех же рассуждений, что силу T _6,7: _тnD

T89 = 48hD ^S, где hD определяем в зависимости от текущей длины заготовки:

при L X >^h n3 , h d =^h n3 , и ^h D =^Ю; при L X >^h n3 , h d =^h D = L X ■

Для непрерывного процесса СПП заготовка имеет бесконечную длину, поэтому T ₈ ,9 =0.

Подставляя найденные силы в уравнение (28), окончательно найдем удельное давление в объеме деформируемого металла при выдавливании заусенца:

о Р

¹  = -A™P

^ S   ^ S^FH

= 2ln X_3C + 2X_3C (1 + — K -) ^ P - - X_{3C    +} d ( d ^ )2.

D_HD_H     D_H  12 h_ΠЗ D_H

В установке СПП валок с ручьем и валок с выступом образуют рабочий калибр прямоугольного сечения шириной b_K , на выходе из которого установлена матрица также прямоугольного сечения высотой h M . Поэтому преобразуем полученные формулы (27) и (35) для расчета технологических и конструктивных параметров процесса СПП. Пусть зазор Δ между матрицей и валками равномерно расположен по всему периметру. Тогда площади калибра F K , матрицы F M и заусенца (зазора) F ЗС будут соответственно равны:

F _K = ( b_K +А)( Н м +А), F m = Ь_кН м , F 3C = F_K - F m - А( b_K + Н м ). (36)

Вытяжка при выдавливании заусенца λ ЗС будет равна:

FK         bKhM

F k — F m " ⁺ А( Ь к + Н м ).

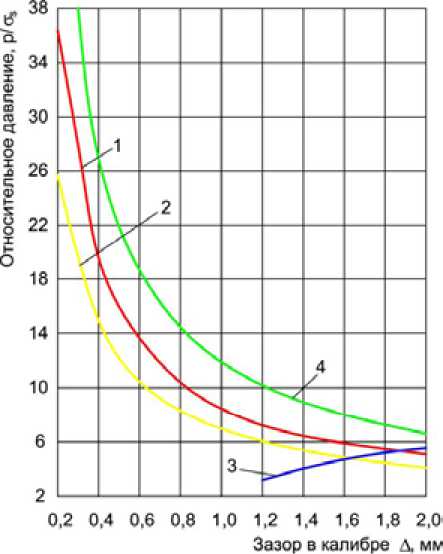
Рис. 4. Изменение относительного удельного давления при выдавливании заусенца

Кроме того, учтем следующие соотношения:

₍ D ) 2 = F = 1 ₊ ^А( b K ⁺ h ) = ^А _п _ 2( Ь к + h M + 2А) d     F m      Ь к + h M     ^ зе -1,            п

С учетом вышеприведенных выражений получим следующие зависимости для определения удельного давления при выдавливании заусенца из калибра прямоугольного сечения:

• -    по методике М.В. Сторожева [4]

Рзе _ вА — 1)             Азе. , 2 U    1,15 Ке _ъ

^s "   А зе        ^ ⁽ А зе — 1) ⁺ А ⁺ J^ + .    ]’

• -    по методике И.Л. Перлина [3]

Р зе               2 пА зе 1 рп /Ь_{к          +} ( А зе — 1) 32

= 21П А_г + А_г +

^ S           1 + h M/ Ь к + 2 А/ Ь к ^N         6 А зе

На рис. 4 представлены графики относительного удельного давления в начальный момент 1

и (40) - кривая 2, а также кривая 3 – изменение удельного давления прессования в зависимости от вытяжки прессования, которая изменялась в пределах А_ПР = 4 + 12, при изготовлении прутка из алюминиевого сплава АД31 на установке СПП. При этом калибр имел ширину b =20мм, высота матрицы h =22 мм, а длина контакта матрицы с калибром l ПР =3,0 мм. Кривая 4 – это изменение относительного удельного давления при образовании заусенца, рассчитанное по формуле (40) и при длине контакта матрицы с калибром l ПР =6,0 мм.

Выводы

Анализируя полученные результаты, можно отметить следующее:

• 1.    При определении удельного усилия для образования заусенца на основе метода баланса работ по методике М.В. Сторожева [4] более высокие результаты расчетов (на 20÷30 %), чем рассчитанные по методике И.Л. Перлина [3].

• 2.    С увеличением длины контакта матрицы с калибром удельное усилие для образования заусенца возрастает.

• 3.    Оптимальный односторонний зазор при СПП должен составлять 5 < А/2 < 0,7 мм. При меньшем значении возможно образование надиров [5], при большем – появление заусенца.

Статья опубликована при поддержке Программы развития Сибирского федерального университета

Siberian Federal University, 79 Svobodny, Krasnoyarsk, 660041 Russia

The report presents the design procedure of the optimal choices in fixed gage for the process of combine rolling-and extrusion with a glance of the rheology of the deformed metal. The example of calculation of optimal choice in fixed gage for combine rolling and extrusion for making the profiles from aluminum alloy is resulted.