Выбор параметров LC-фильтра для ШИМ сигнала

Широтно-импульсная модуляция (ШИМ) в последнее время находит все большее применение при осуществлении регулирования систем электроснабжения [1–3]. Поскольку источник ШИМ сигнала не удовлетворяет требованиям системы по коэффициенту гармоник, то между системой и источником ШИМ сигнала используют фильтры. Наиболее простой и удобной схемой такого фильтра является Г-образная схема LC-фильтра (рис. 1). Выбору его параметров посвящено большое количество публикаций [1, 4–6].

Z

Рис. 1. Схема LC-фильтра

В работе [1] выбор параметров фильтра L = 2 - 10 ^-4 Гн и C = 2 - 10 ^{- 2} Ф был выполнен по частоте среза f_c = 159 Гц фильтра. Фильтр с такими параметрами безусловно будет подавлять высшие гармоники, но на основной гармонике работает фактически в режиме резонанса f ₀ = 79 Гц, что отрицательно сказывается на габаритных размерах элементов фильтра.

В работе [4] подбор параметров фильтра осуществлялся только по коэффициенту гармоник, что дает неоднозначное решение задачи и не учитывает важных для практики свойств фильтра. В работе [5] предложена, а в работе [6] усовершенствована методика подбора параметров фильтра. Фильтр должен удовлетворять требованиям: по коэффициенту гармоник, жесткости характеристики фильтра под номинальной нагрузкой и соотношению между действующими значениями входного тока и тока нагрузки.

Методика начинается с подбора фильтра, удовлетворяющего требованиям по коэффициенту гармоник. При этом многие фильтры потом отбраковываются из-за недостаточной жесткости характеристики фильтра под нагрузкой. Поэтому в настоящей работе предложен другой алгоритм подбора параметров фильтра. На первом этапе определяются требования к индуктивному X_L и емкостному X_C сопротивлениям элементов фильтра, обусловленные энергообменом на первой гармонике при заданном сопротивлении Z H = Z H e^ ⁰ номинальной нагрузки фильтра. На втором этапе определяют коэффициент гармоник.

Чтобы потеря напряжения в фильтре составляла не более а , = 1 процента от входного напряжения, сопротивления элементов фильтра должны удовлетворять соотношению X L / X_C <  0,01 а 1 .

Чтобы уменьшение напряжения U_H фильтра под номинальной нагрузкой составляло не более а 2 = 1 процента от напряжения U xx в режиме холостого хода, должно выполняться соотношение X L / Z H <  0.01 а ₂.

Указанные требования можно записать через А-параметры четырехполюсника в виде

|А\ - 1 <  0,01 а ! и | Р | < 0,01 а ₂ Z H . (1)

Для каждой конкретной нагрузки Z = Ze ⁰ задача на соответствие параметрам жесткости ( U xx - U_H )/ U_H <  0,01 а ₂ имеет более сложное решение, но во всем диапазоне нагрузок Z >  Z H 0 <ф< 30 ° оценка (1) дает простую аналитическую запись требований к параметрам фильтра.

Численным экспериментом несложно проверить, что в указанной области требуемые величины для жесткости характеристики под нагрузкой действительно удовлетворяются. При расчетах потери в катушке и конденсаторе приняты равными tg( ^ j ) = 0,01 и коэффициент мощности нагрузки cos( ^ ) = 0,8.

В таблице (строка 1) представлена зависимость изменения напряжения под нагрузкой K = 100 % (U xx - U_H ) / U_H от относительного изменения индуктивного а L = X L /0,01 Z H и емкостного а C = X C / Z H сопротивлений фильтра. Зависимость изменения напряжения может быть аппроксимирована функцией K ( а L ) = K ₀ а L , где K ₀ - значение коэффициента при а L = 1 и а C = 1.

Следующим практическим требованием к параметрам фильтра является минимизация его габаритов, т. е. минимизация суммы модулей реактив- ных мощностей его элементов. Это требование было исследовано путем численного моделирования. В области допустимых значений параметров (1) было рассчитано отношение суммы модулей реактивных мощностей QS = XLI12 + U2 / XC к полной мощности нагрузки S2 = U212. Отношение W = QS / S2 показывает энергетическую эффективность фильтра. Чем меньше это отношение, тем лучше фильтр как звено в энергообмене между источником и нагрузкой. Численный эксперимент показал, что с увеличением емкостного сопротивления XC фильтра отношение QS / S2 уменьшается во всем диапазоне нагрузок. При этом изменение индуктивного сопротивления XL фактически не сказывается на данном процессе.

Результаты численного эксперимента представлены в таблице (строка 2). Параметр W = Q S / S 2 вычислен при нескольких относительных изменениях индуктивного а _L = X L /0,01 Z_H и емкостного а C = X C / Z H сопротивлений фильтра. Зависимость коэффициента энергоэффективности может быть аппроксимирована функцией W ( а C ) = W ₀ / а C , где W ₀ - значение коэффициента при а L = 1 и а C = 1.

Потери активной мощности на элементах фильтра в основном происходят на основной гармонике. Потери в элементах фильтра учитывались при помощи коэффициента потерь, равного отношению K P = A P / S ₂: активной мощности потерь Д Р = Re( Z L ) I 1² + Re( Y C )U 2 к полной мощности нагрузки S ₂ = U ₂ 1 ₂. Результаты численного моделирования представлены в таблице (строка 3). Зависимость коэффициента потерь может быть аппроксимирована функцией

Результаты численного моделирования

Зависимость изменения напряжения под нагрузкой	а C /а L 0,5     1     2 0,5 0,31 0,308 0,307 1 0,625 0,619 0, 616 2 1, 276 1, 249 1, 236
Зависимость коэффициента энергоемкости фильтра	а C (a L   0,5    1     2 0,5 2, 013 1, 004 0,503 1 2, 026 1, 008 0, 507 2 2, 052 1, 016 0,513
Зависимость потерь активной мощности в элементах фильтра	а C /а L 0,5 1    2 0,5 0,04 0,02 0,01 1     0, 041 0,2 0,01 2    0,042 0,02 0,01
Зависимость амплитуды передаточного коэффициента по напряжению для 50-й гармоники	а C /а L 0,5     1     2 0,5 0,036 0,075 0,16 1 0, 018 0, 036 0, 075 2 0,009 0,018 0, 036

Сафонов В.И.

K P ( a C ) = K P ₀/ a C , где K P ₀ - значение коэффициента при a L = 1 и a C = 1. Зависимости коэффициентов энергоэффективности W ( a C ) и потерь K P ( a C ) совпадают. Следовательно, увеличивая емкостное сопротивление фильтра X C можно не только уменьшить габаритные размеры фильтра, но и уменьшить потери активной мощности в элементах фильтра.

Далее проведем численное исследование зависимости коэффициента гармоник от сопротивлений элементов фильтра. Нормированная АЧХ коэффициента передачи по напряжению K U ( k ) = U ₂ ( _к ) / U 1( _к ) представлена на рис. 2. Нормировка выполнена на значение коэффициента для основной гармоники.

Графики построены при значениях параметров: 1) X L = 0,01 Z H , X C = Z H (крестики); 2) X L = 0,01 Z H , X C = 2 Z H (плюсики); 3) X L = 0,02 Z H , X C = Z H (точки); 4) X L = 0,02 Z H , X C = 2 Z H (линия). Построение выполнено для гармоник к >  50 в предположении, что тактовая частота ШИМ сигнала f_c >  2500 Гц более чем в 50 раз больше, чем частота основной гармоники f ₁ = 50 Гц.

При численном эксперименте были учтена зависимость потерь в конденсаторе и катушке индуктивности от частоты. Согласно [7] активная проводимость конденсатора для высших гармоник G k = G ₀ к , где G ₀ - активная проводимость для основной гармоники. Также согласно [7] активное сопротивление катушки для высших гармоник R k = R ₀ J k , где R - активная проводимость для основной гармоники. Учет зависимости потерь от частоты приводит к уменьшению коэффициента гармоник на несколько процентов.

Данные численного расчета нормированного АЧХ коэффициента передачи по напряжению представлены в таблице (строка 4) для 50-й гармоники. Зависимость может быть аппроксимирована функцией N(aC, aL) = N0aC / aL, где N0 - значе ние коэффициента при aL = 1 и aC = 1. Из рис. 2 видно, что полученное для 50-й гармоники зависимость для параметров элементов фильтра сохраняется и для гармоник к > 50 . Следовательно, для коэффициента гармоник KГ = /^ U2(к) / U2(1)

• V к = 2

также будет выполняться аппроксимационная формула K Г ( a C , a _L ) = K Г ₀ a C / a _L .

В результате численного анализа были получены аппроксимационные формулы для относительных изменений основных характеристик фильтра:

K(aL) = K0aL (коэффициента жесткости);(2)

W(aC) = W0 / aC (коэффициента энергоэффективности);(3)

KГ (aC, aL) = KГ0aC / aL (коэффициента гармоник);(4)

KP (aC) = KP0/ aC (коэффициент потерь).(5)

Формулы (2)-(5) справедливы при незначительном (не более чем в 2 раза) отклонении параметров фильтра от базовых значений и являются фактически результатом условной аппроксимации характеристик фильтра. Формулы (2)-(5) применимы только в области допустимых значений параметров фильтра, когда индуктивное сопротивление фильтра много меньше сопротивления номинальной нагрузки X L <<  Z H , а емкостное сопротивление сравнимо или больше номинального сопротивления 0,5 Z H <  X C . Формулы (2)-(5) удобны при инженерном расчете фильтра, когда необходимо подобрать оптимальное соотношение свойств фильтра.

Таким образом, алгоритм синтеза фильтра состоит из двух основных этапов:

• 1)    определение предварительных параметров фильтра по соотношениям (1),

• 2)    уточнение параметров фильтра по аппроксимационным формулам (2)-(5).

Если в результате не будут получены требуемые характеристики фильтра, необходимо изменить параметры предварительной оценки и повторить п. 2 алгоритма.

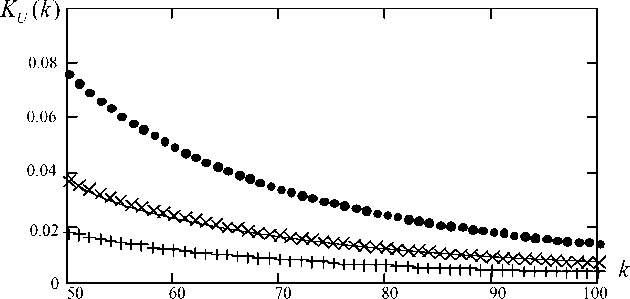
Рис. 2. Зависимость коэффициента гармоник

По сравнению с работой [6] данный алгоритм намного проще. Следует отметить, что при получении аппроксимационных формул (2)–(5) было введено обязательное требование k >  50 для высших гармоник. Т. е. предложенный алгоритм может использоваться только для высокочастотных ШИМ источников. Алгоритм, рассмотренный в работах [5, 6] позволяет синтезировать фильтры при произвольном наборе частот высших гармоник.

На рис. 3 показана область возможных значений индуктивных и емкостных сопротивлений фильтра.

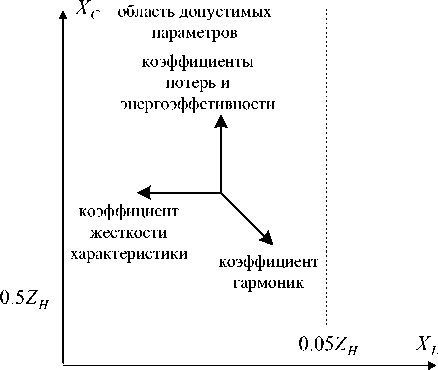
Рис. 3. Диаграмма свойств фильтра

Стрелками показаны направления улучшения каждой из обозначенных ранее характеристик фильтра. Из рис. 3 видно, что одновременное улучшение всех характеристик фильтра невозможно. Требования к коэффициенту гармоник закреплены в ГОСТ 13109-97 и не могут быть пересмотрены. В случае использования источника ШИМ для регулирования систем энергоснабжения напряжением 10 кВ [1–3] или 0,4 кВ существенным становится требование к габаритным размерам, которое в рассмотренном алгоритме учтено коэффициентом энергоэффективности. Улучшение энергоэффективности фильтра невозможно без одновременного ухудшения жесткости характеристики фильтра под нагрузкой или коэффициента гармоник.

Снижение жесткости характеристики под нагрузкой может быть устранено усложнением системы управления. Введя датчики тока и напряжения нагрузки, возможно по определенному алгоритму изменять глубину модуляции ШИМ сигнала, увеличивая амплитуду источника и компенсируя тем самым снижение напряжения под нагрузкой.