Выбор параметров накопителя энергии для нового периферийного стыковочного механизма

ЯСКЕВИЧ А.В.

ЧЕРНЫШЕВ И.Е.

Кинематика нового периферийного стыковочного механизма

Во всех известных системах стыковки, доведенных до практического применения, первичная механическая связь агрегатов — сцепка — обеспечивается расположенными на буферных звеньях стыковочного механизма (СтМ) механическими защелками, которые зацепляются за механические упоры на пассивных стыковочных агрегатах (СтА). Для относительного выравнивания стыковочных интерфейсов, т. е. приведения СтМ в определенное положение, а также для срабатывания защелок, необходимо затратить механическую энергию. Пассивная сцепка осуществляется за счет кинетической энергии активного космического аппарата (КА), и после ее достижения оставшуюся часть этой энергии необходимо демпфировать [1]. В настоящее время разработан международный стандарт систем стыковки (IDSS) [2], который определяет использование периферийного типа СтМ. В новых, соответствующих этому стандарту, СтМ IBDM [3, 4] и NDS [5–7] используется активная сцепка, когда стыковочное кольцо с защелками при первом контакте СтА выдвигается вперед навстречу пассивному агрегату. Эти механизмы имеют сложное управление, приводятся в движение шестью электродвигателями (ЭД), пассивные устройства демпфирования в их управляемых кинематических цепях отсутствуют. Поэтому поглощение энергии сближения производится этими же ЭД, работающими в генераторном режиме, в котором они создают малые моменты сопротивления. Частично это компенсируется большой величиной приведенной к кольцу инерции ЭД и трением в передачах.

Скорость выдвижения кольца периферийного СтМ и эффективность поглощения энергии сближения можно значительно увеличить, если использовать пассивные механические устройства — пружинные механизмы (ПМ) с управляемой блокировкой их отдачи. Принцип действия такого СтМ основан на аккумулировании энергии сближения активного КА, т. е. на реализации стыковки как одноударного, однонаправленного процесса. Ее отличают следующие основные особенности:

• •    кинематической основой СтМ является платформа Гью–Стьюарта (ПГС) [8, 9], конструктивная реализация параллельных кинематических цепей которой далее называется штангами;

• •    штоки, поступательно перемещающиеся вдоль продольных осей штанг, представляют собой винты, и их движение через шарико-винтовую передачу (ШВП) преобразуется во вращение валов спиральных ПМ, расположенных на корпусах штанг;

• •    при максимально выдвинутых штоках платформа имеет наименьшую подвижность, что ухудшает сцепку. Поэтому

СтМ имеет три фиксированных положения: конечное (КП) — в котором штоки штанг полностью втянуты; переднее (ПП) — штоки максимально выдвинуты и исходное (ИП) — промежуточное перед началом стыковки. При нахождении в КП и ИП отдача сжатых ПМ и, соответственно, выдвижение штоков блокируются включенными управляемыми обгонными муфтами (УОМ);

• •    СтМ втягивается в КП тремя тросами, приводимыми в движение одним электроприводом. При этом ПМ штанг накапливают энергию, которая впоследствии используется для приведения СтМ из КП в ИП, а затем и из ИП в ПП;

• •    для улучшения сцепки используется быстрое выдвижение кольца из ИП вперед, в сторону ПП, оно обеспечивается освобождением оставшейся потенциальной энергии ПМ. Для этого при первом контакте кольца с пассивным агрегатом УОМ выключаются, снимая блокировки отдачи всех ПМ, штоки всех штанг выдвигаются, и кольцо быстро перемещается навстречу пассивному агрегату для сцепки с ним. Подстройка кольца СтМ под положение кольца пассивного СтА осуществляется за счет различной закрутки валов ПМ;

• •    УОМ после сцепки вновь включаются, блокируя отдачу ПМ, которые после этого при просадке кольца и втягивании штоков аккумулируют энергию сближения КА, не возвращая ее в механическую систему;

• •    низкое энергопотребление обеспечивается использованием только одного привода, работающего при выдвижении и стягивании СтМ, а также тем, что УОМ не потребляют энергию при сохранении любого из двух своих состояний.

Упрощенная кинематическая схема пары штанг нового периферийного СтМ показана на рис. 1. Подробное описание функционирования СтМ приведено в работе [10].

Сигнал с устройства контактного (УК) каждой штанги формируется, когда ход штока достигает величины, соответствующей ИП СтМ. Перед началом стыковки при выдвижении в ИП появление сигналов с УК в каждой штанге включает соответствующую УОМ, и отдача ПМ блокируется. При блокировке ПМ всех штанг СтМ фиксируется в ИП. В начале стыковки потеря хотя бы одного сигнала с УК вследствие изменения длины штока интерпретируется как наличие первого контакта СтА и приводит к выключению всех УОМ для снятия блокировки отдачи ПМ всех штанг и быстрому выдвижению кольца навстречу пассивному СтА.

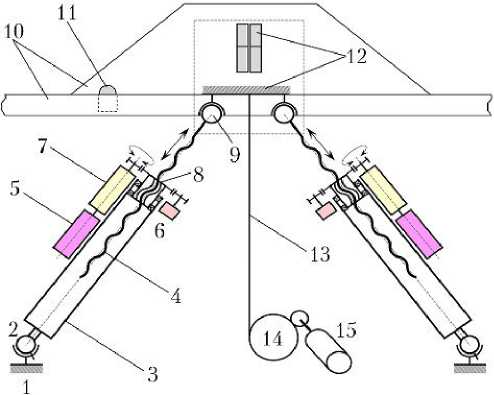
Рис. 1. Упрощенная кинематическая схема пары штанг стыковочного механизма (СтМ): 1 — основание СтМ; 2 — универсальный шарнир; 3 — корпус штанги; 4 — винт (шток); 5 — управляемая обгонная муфта; 6 — устройство контактное; 7 — пружинный механизм; 8 — шариковинтовая передача; 9 — сферический шарнир; 10 — стыковочное кольцо с направляющими выступами; 11 — датчик совмещения колец; 12 — корпус механизма защелок; 13 — трос; 14 — барабан намотки троса; 15 — электропривод устройства стягивания

Факт сцепки определяется по срабатыванию трех датчиков совмещения колец и вызывает включение УОМ и блокировку отдачи ПМ всех штанг. После этого штоки штанг могут только втягиваться, а ПМ — накапливать потенциальную энергию, преобразованную из кинетической энергии сближения активного КА. Через фиксированный интервал времени после сцепки, достаточный для полного поглощения энергии сближения, блок управления СтМ подает сигнал на электропривод устройства стягивания, которое уменьшает свободную длину тросов, прикрепленных к стыковочному кольцу, приближая его к плоскости стыка. Схема этого устройства в данной работе не рассматривается.

Шесть штанг с поступательно движущимися штоками и ПМ, отдача которых блокируется УОМ, представляют собой накопитель энергии сближения активного КА. Хотя энергия накапливается в спиральных ПМ, их валы связаны со штоками через ШВП и редукторы, передаточное отношение которых может изменяться в процессе конструирования. Поэтому на этапе проектирования энергоемкость этого накопителя определяется параметрами, задающими изменение создаваемой ПМ силы сопротивления перемещению штока штанги (далее для краткости — силы сопротивления штанги).

Три фиксированных положения СтМ — КП, ИП и ПП — определяют наличие двух областей в его рабочем пространстве. В области между ИП и ПП механизм должен иметь максимальную податливость для обеспечения подстройки кольца под кольцо пассивного СтА и облегчения сцепки. Минимальная величина осевой силы сопротивления штанги должна быть реализована в ПП и создавать сопротивление, необходимое для срабатывания механических защелок на кольце. Поглощение кинетической энергии сближения активного КА осуществляется в основном при движении СтМ в области между ИП и КП. Часть энергии, поглощенная в области между ИП и ПП, составляет проектный запас. Движение СтМ от начала стыковки до завершения поглощения энергии сближения является неуправляемым, и поэтому оно не должно приводить к контактам звеньев между собой и с корпусом СтА и, соответственно, к неконтролируемым нагрузкам. Вследствие случайного характера изменения параметров начальных условий стыковки и априорно неизвестного их распределения должна быть обеспечена возможность поглощения максимально возможной величины энергии сближения активного КА до появления контактов.

Это обусловливает необходимость реализации нелинейной зависимости создаваемой спиральным ПМ силы f_S сопротивления штанги от величины t_S хода ее штока (рис. 2).

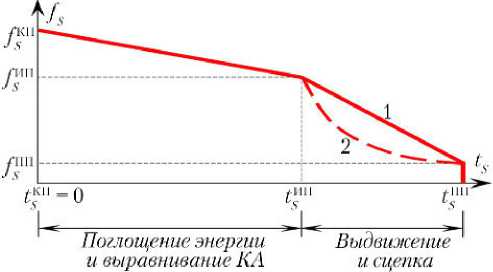
Рис. 2. Изменение силы сопротивления ходу штока штанги стыковочного механизма: 1, 2 — различные варианты изменения Примечание. f_S — сила сопротивления штанги; t_S — ход штока штанги; КП — конечное положение; ИП — исходное положение; ПП — переднее положение.

Изменение силы f_S в области между ИП и ПП уточняется по результатам моделирования динамики стыковки. Оно должно обеспечивать приемлемое время выдвижения кольца и сцепки. При смещении от ИП в КП сила f_S нарастает линейно, что позволяет реализовать этот участок спиральной пружиной с постоянными конструктивными параметрами.

Основные этапы выбора параметров накопителя энергии

Стыковочный механизм может использоваться для стыковки КА с различными инерционными характеристиками. Двумя граничными вариантами можно считать стыковку активного КА к значительно более массивному пассивному объекту (например, транспортный корабль — к МКС), и обратный ему, когда масса пассивного КА меньше активного. В первом случае , в соответствии с работой [11], эквивалентная масса двух тел будет максимальной и близкой к массе активного КА. Тогда при максимальной скорости сближения максимальной будет и кинетическая энергия, которую необходимо поглотить СтМ. При этом время от первого контакта СтА до сцепки (время сцепки) будет минимальным и, по экспертной оценке, не превысит 1 с. Во втором граничном случае эквивалентная масса двух тел будет близка к меньшей массе пассивного объекта. Вследствие этого может значительно увеличиться время сцепки и, если для ее ускорения предполагается включение двигателей активного КА, то возрастет и скорость сближения последнего. В то же время контактное взаимодействие СтА до сцепки приведет к нарастанию скорости пассивного КА малой массы в направлении движения активного, что уменьшит относительную скорость сближения. Поэтому величина кинетической энергии, которую должен будет поглотить СтМ, будет в этом случае меньше, чем в первом. В обоих случаях считается, что сцепка достигается. Условия, которые этому способствуют, а также время сцепки не являются предметом рассмотрения в данной работе.

Исходя из всего вышеизложенного, при выборе параметров силы сопротивления штанг используется расчетная схема, в которой активный КА стыкуется к пассивному, имеющему бесконечную массу.

Пружинные механизмы штанг должны быть способны поглотить кинетическую энергию, соответствующую максимальным значениям инерционных характеристик и скоростей активного КА, в т. ч. с учетом включения его реактивных двигателей до сцепки.

Данная расчетная схема представляет собой замкнутую систему тел, в которой перераспределение энергии осуществляется от первого контакта СтА до ее полного поглощения. При расчете параметров накопителя энергии трение в СтМ не учитывается, что создает определенный запас энергоемкости.

Перед стыковкой СтМ находится в ИП, которому соответствуют одинаковый ход t_S ^ИП штоков всех штанг. Если в процессе контактного взаимо-дейс_–твия СтА ход t_Si штока i -й штанги ( i ∈ 1, 6 ) меньше t_S ^ИП, то это означает, что эта штанга накопила часть кинетической энергии КА. При увеличении хода i -го штока (например, при сцепке), т. е. при t_S,i >  t_S ^ИП, освобождаемая часть энергии ПМ должна быть вновь аккумулирована при последующем поглощении энергии сближения активного КА и возврате к t_S ^ИП. Это позволяет считать, что каждая штанга накапливает энергию сближения активного КА только при уменьшении хода ее штока от ИП, т. е. при t_S,i ≤ t_S ^ИП .

В ПГС возможно 36 различных относительных перемещений в шарнирах. Только 6 из них —–поступательные перемещения tS,i, i = 1, 6 штоков штанг — являются независимыми, управляющими. Это объясняется тем, что без учета внешней нагрузки управляемое тело, в данном случае стыковочное кольцо, приводится в д–вижение внутренними силами fSi, i = 1, 6 СтМ, действующими на штоки вдоль их продольных осей. Ходы tS,i определяют зависимые переменные — угловые перемещения в шарнирах вращения. Поэтому совокупность значений этих ходов далее для краткости называется конфигурацией платфор–мы. Независимые переменные tS,i, i = 1, 6 образуют пространство, границы которого обусловлены наличием их недопустимых сочетаний. Помимо этого, перемещения СтМ ограничены контактами его звеньев, являющихся объемными телами, между собой и с корпусом СтА. Таким образом, внутри пространства независимых, управляющих переменных платформы существует пространство такой же размерности, которое называется далее рабочим пространством (РП) СтМ. Выходы на его границы могут привести к неконтролируемым нагрузкам и поэтому должны быть исключены в процессе функционирования механизма. Приближению к ним противодействуют силы сопротивления штанг, создаваемые расположенными на них ПМ. Предполагается, что СтМ, вследствие случайного характера изменения параметров начальных условий стыковки, может оказаться в любой точке своего РП, поэтому на первом этапе проектирования накопителя энергии определяются и запоминаются границы этого пространства.

Далее с учетом линейного изменения силы сопротивления каждой штанги при ее движении между КП и ИП необходимо было бы определить три параметра, например, силы f_S ^ИП и f_S ^КП, создаваемые ее ПМ в ИП и КП, и ход штока t_S ^ИП между этими положениями. Для повышения обоснованности выбора число изменяемых параметров уменьшается до двух на основе дополнительного ограничения f _R ^К _x ^П = f _R ^И _x ^П (рис. 3), что обеспечивает примерно одинаковую нагрузку на привод стягивания СтМ. При этом появляется возможность контролировать максимальную величину силы сопротивления СтМ при его продольном осевом движении, когда при сохранении одинаковой длины всех штанг центр стыковочного кольца перемещается из ИП в сторону КП. Это ограничение обусловлено тем, что кинетическая энергия КА определяется в основном его осевой продольной скоростью сближения.

При осевом продольном движении выровненного кольца СтМ из ИП в КП все штоки втягиваются на одинаковую величину, спиральные пружины ПМ закручиваются, увеличивая силы сопротивления штанг. Но одновременно с этим по мере движения уменьшается проекция этих сил на продольную ось механизма вследствие увеличения по отношению к ней углов наклона штанг. В результате, в некоторой промежуточной точке xRmax осевого перемещения сила сопротивления кольца достигает своего максимума fmax (рис. 3), который должен удовлетворять , заданному проектному огра- ничению max ≤ fпро ект. R,x R,x

С учетом условия параметры tSИП, fSИП и штока i-й штанги fRК,xП = fRИ,xП через текущий ход tS,i выражаются сила

сопротивления f_S,i ( t_S ^ИП, f_S ^ИП, t_S,i ) при ходе t_Si штока i -й штанги и сила осевого сопротивления f_R,x ( t_S ^ИП, f_S ^ИП, t_S,i ) выровненного кольца. Используя f_S,i ( t_S ^ИП, f_S ^ИП, t_S,i ), через t_S ^ИП и f_S ^ИП выражается работа сил сопротивления всех штанг при различных ходах их штоков, и в итоге — зависимость силы f_S ^ИП сопротивления штанг в ИП от величины поглощаемой энергии сближения КА и величин текущих ходов штоков. Выражение для f_R,x ( t_S ^ИП, f_S ^ИП, t_S,i ) позволяет определить максимум f _R ^m _,x ^ax осевой силы при заданных f_S ^ИП, t_S ^ИП и ход штоков, при котором он достигается. Это дает возможность контролировать выполнение ограничения f _R ^m _x ^ax ≤ f _R ^п _, ^р _x ^{о ект}.

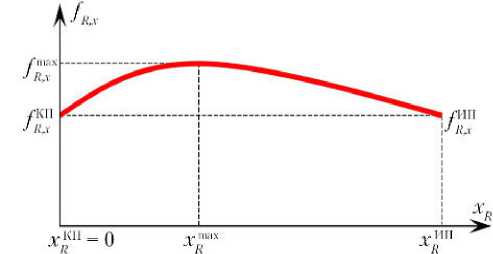
Рис. 3. Изменение силы сопротивления осевому перемещению кольца стыковочного механизма при одинаковых ходах штоков его штанг и при равенстве этой силы в исходном (ИП) и конечном (КП) положениях

На основе полученных зависимостей реализуется процедура выбора параметров накопителя энергии СтМ — минимального значения t_S ^ИП, при котором f_S ^ИП такова, что зависящая от них f _R ^m _x ^ax удовлетворяет заданному ограничению. В результате обеспечивается максимальный ход штоков и кольца из ИП в ПП, что улучшает условия сцепки.

Определение границрабочего пространства СтМ

Границы пространства независимых переменных ПГС соответствуют таким значениям длин штанг, которые несовместимы с положением управляемого тела — стыковочного кольца. Если эти границы определять варьированием значений независимых переменных, то для проверки нарушения условия сборки необходимо вычислять декартовы координаты стыковочного кольца, соответствующие сочетаниям этих длин, т. е. решать прямую задачу кинематики параллельного манипулятора. Вследствие угловых движений кольца имеет место нелинейное уравнение связи fR(rR, αR, lM) = 0, в котором rR = [xR, yR, zR]T — вектор перемещения центра кольца; αR = [ψR, θR, ϕR]T — вектор, составленный из углов поворота кольца по рысканию, тангажу и крену; lM = [lS,1, …, lS,6]T — вектор, составленный из поступательных перемещений штоков штанг.

Решение прямой кинематической задачи, если оно существует, может быть найдено итерационным способом

[ r _R , α _R ] _k ^T = [ r _R , α _R ] ^T _{k –1} – J _R ^–1 f _R ( r _{R,k –1}, α _{R,k –1}, l _{M,k –1}), где k — номер итерации;

J _R = ∂ f _R ( r _{R , k –1}, α _{R,k –1}, l _M )/∂ l _M — (6×6) — матрица Якоби.

При недопустимых сочетаниях независимых переменных решение отсутствует, и итерационный процесс не сходится. Границе пространства соответствуют также сингулярные (вырожденные) конфигурации ПГС, в которых определитель матрицы Якоби J _R равен нулю. Это означает, что проекции некоторых направляющих векторов штанг, вдоль которых осуществляются бесконечно малые виртуальные перемещения δ l _M , хотя бы на один из векторов бесконечно малых декартовых виртуальных перемещений δ r _R и δ α _R стыковочного кольца, равны нулю. Сингулярной, например, является конфигурация, при которой пара штанг лежит в плоскости, параллельной стыковочному кольцу. При переходе через нее ПГС может потерять свою функциональность. Сингулярность обусловлена геометрией платформы, т. е. может иметь место при определенных соотношениях размеров звеньев и относительных перемещений в шарнирах. При проектировании СтМ сингулярность, в случае ее выявления, исключается корректировкой конструкции.

Определение границ РП ПГС можно производить более простым способом с помощью решения обратной кинематической задачи (ОКЗ) — расчета величин ходов штоков штанг по заданному положению управляемого тела — стыковочного кольца. Решение ОКЗ существует даже в сингулярных конфигурациях, если положение кольца соответствует ходам штоков, допустимым конструктивными ограничениями.

С учетом этого, при определении границ рабочего пространства СтМ выполняется полный перебор всех возможных сочетаний шести декартовых координат стыковочного кольца, каждая из которых изменяется в заданном с некоторым запасом диапазоне с дискретностью, соответствующей заданной точности. Для каждого сочетания координат кольца решается ОКЗ, и если решение существует, то вычисляются определитель матрицы Якоби, значения зависимых шарнирных переменных, и выполняется проверка наличия контактов звеньев. Если при очередном положении стыковочного кольца в декартовой системе координат имеет место выход ходов штоков штанг за пределы допустимого диапазона или контакт звеньев, то непосредственно предшествующее ему сочетание независимых переменных соответствует границе РП СтМ и запоминается для последующего выбора параметров изменения сил сопротивления штанг. Если СтМ имеет сингулярные конфигурации, то, с учетом конечной величины шага дискретизации декартовых координат кольца, вероятность попадания в точку РП, в которой det( J _R ) = 0, мала. Поэтому на наличие сингулярности указывает смена знака этого определителя при переходе к очередной точке. При обнаружении таких ситуаций выбор параметров накопителя энергии завершается, так как требуется коррекция конструкции СтМ.

Для каждого сочетания значений шести декартовых координат стыковочного кольца проверка принадлежности длин штоков границе РП СтМ осуществляется на основе следующих вычислений.

При решении ОКЗ для ПГС положение стыковочного кольца относительно декартовой системы координат (СК) O_B x_B y_B z_B , связанной с основанием СтМ, задается вектором координат центра r _R ^{( B )} и углами ориентации ψ _R , θ _R , ϕ _R кольца. Положение центров шарниров вращения на осно_–вании задается постоянными векторами l вВ ) ( i - 1, 6 ), а шарниров вращения на кольце — постоянными векторами l RRR ) , определенными в СК O_R x_R y_R z_R с началом в центре кольца (рис. 4).

Здесь и далее верхний индекс в скобках указывает на СК, в которой определен вектор. Преобразование координат из OB xB yB zB в OR xR yR zR определяет матрица τR, элементы которой вычисляются по значениям углов ψR, θR, ϕR в соответствии с принятой последователь- ностью поворотов. В соответствии с этим lRB) = т R lRR ).

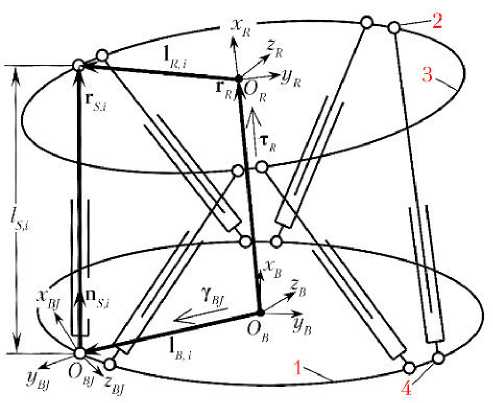
Рис. 4. Векторы и матрицы, используемые для решения обратной кинематической задачи платформы Гью–Стюарта: 1 — основание СтМ; 2 — сферический шарнир; 3 — стыковочное кольцо; 4 — универсальный шарнир

Расстояния между центрами нижних и верхних шарниров вращения, т. е. длины l_S,i штанг, равны модулям соответствующих векторов r _S,i из центров нижних шарниров в центры верхних ^^^^^^^^^^^^^^^^^^^^^™

S - I r 5В * I -I— 1 В‘ ¹ + r RB ) + 1 Rв ⁾ L i - 1,6.

Ходы штоков штанг определяются разностями ^^^^^^^^^^^^^^^^^^^^^™ tS,i = lS,i – lSКП, i = 1, 6, в которых lSКП — минимальное расстояние между нижними и верхними шарнирами (длина штанги) в КП СтМ. Если ходы не удовлетворяют условию 0 ≤ tS,i ≤ tSПП, то имеет место выход за границу РП платформы.

Попутным результатом решения ОКЗ являются единичные векторы штанг ^^^^^^^^^^^^^^^^^^^^^™

n ( В ) - r ( В ) / l_s, i - 1, 6,

S,i S,i S _, i которые используются для расчета матрицы Якоби и при расчете углов поворота в шарнирах вращения для последующего обнаружения контактов звеньев.

Матрица Якоби J _R может быть вычислена различными способами [12–14]. При этом определители различных вариантов этой матрицы могут отличаться на ненулевые множители, не влияющие на их близость к нулю. В работе использован наиболее простой способ [14], в соответствии с которым

J R =

П ( В ) п 5 ,1	n< В ) n 5 ,2	n< B ) n 5 ,3	n < B ) 5 ,4	( В ) n 5 ,5	n( В ) n 5 ,6
I ( в )п< в ) R ,1 n 5 ,1	f <  В )n< В ) R ,2 n 5 ,2	f <  В )n( В ) R ,3 n 5 ,3	T ( в )n< В ) R ,4 n 5 ,4	f ( в )n( В ) x R ,5 n 5 ,5	1 R’ б, п 5'В ’

T

•

Значения зависимых угловых шарнирных переменных ПГС необходимы для расчета матриц направляющих косинусов, с использованием которых вычисляется положение звеньев СтМ в общей СК при обнаружении их контактов. Далее решение описывается для углов в шарнирах одной из штанг СтМ. Ее индекс не указывается для упрощения записи получаемых соотношений.

Нижний шарнир штанги в основании платформы является универсальным, т. е. имеет две степени подвижности по углам тангажа и рыскания — ψ _B,y , θ _B,z , соответственно. Связанная с ним СК O_BJ x_BJ y_BJ z_BJ нижнего шарнира СтМ преобразуется в СК O_S x_S y_S z_S штанги с помощью матрицы направляющих косинусов α _BJ,S , которая выражается через углы следующим образом:

α = BJ,S	cosθ B,z cosψ B,y – s i n θ B ,z c o s ψ B ,y	sinθ B,z c o s θ B ,z	–cosθ B,z sinψ B,y s i n θ B ,z s i n ψ B ,y
	sinψ B,y	0	cosψ B,y

Столбцы транспонированной матрицы α _B ^T _JS составляются из единичных векторов СК O_Sx_Sy_Sz_S , выраженных в СК O_BJ x_BJ y_BJ z_BJ , т. е. ее первый столбец равен n ⁽ _S ^{BJ )} = γ _BJ n ⁽ _S ^{B )}, где γ _BJ — постоянная матрица преобразования из СК O_B x_By_Bz_B основания СтМ в СК O_BJ x_BJ y_BJz_BJ нижнего шарнира, а n ⁽ _S ^{B )} = [ n_B,x , n_B,y , n_B,z ] ^T . Поэтому компоненты вектора n ⁽ _S ^{BJ )} равны n_B,x = cosθ _B,z cosψ _B,y ; n_B,y = sinθ _B,z , n_B,z = –cosθ _B,z sinψ _B,y , а значения углов в нижнем шарнире определяются соотношениями ψ _B,y = –arctg( n_B,z / n_B,x ) и θ _B,z = arcsin n_B,y и позволяют рассчитать остальные элементы матрицы α _BJS .

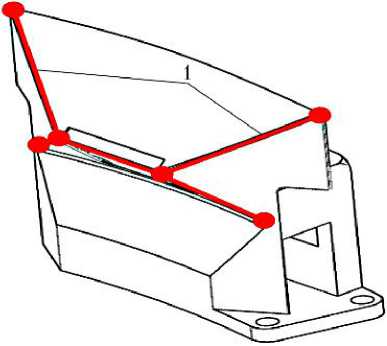
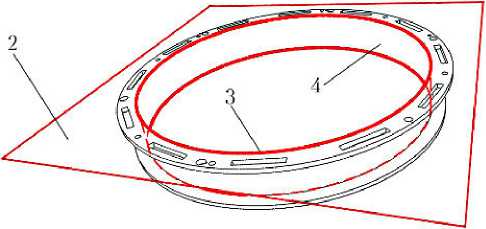
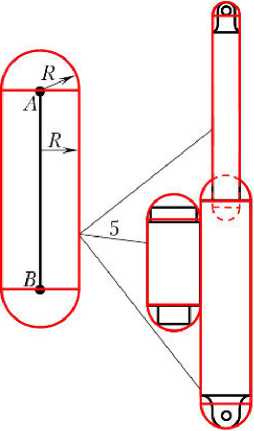
Для обнаружения контактов используются простые аналитические решения, основанные на представлении звеньев СтМ и корпуса СтА совокупностью геометрических примитивов. К традиционно используемым примитивам (отрезку прямой, плоскости, грани-окружности, цилиндру) добавлен новый — цилиндр со сферическими торцами (ЦСТ), в виде которого представляются поверхности штока, корпуса штанги, ПМ и УОМ, направляющих штырей и штырей электро- и гидросоединителей (рис. 5). Параметры всех примитивов определяются в общей СК, связанной с основанием СтМ. При этом используются матрица преобразования поворота стыковочного кольца и описанные выше матрицы αBJ,S.

а)

б)

в)

Рис. 5. Описание сложных поверхностей геометрическими примитивами: а — упор защелок на корпусе СтА; б — корпус СтА; в — штанга СтМ; 1 — отрезок прямой; 2 — плоскость; 3 — грань-окружность; 4 — цилиндр; 5 — цилиндры со сферическими торцами, аппроксимирующие поверхность штанги

При обнаружении контактов анализируются минимальные расстояния между следующими парами примитивов: «отрезок – окружность», «отрезок – отрезок», «отрезок – цилиндр», «отрезок – ЦСТ», «ЦСТ – ЦСТ», «ЦСТ – плоскость». Для пар, в которые не входит ЦСТ, используются алгоритмы, аналогичные описанным в работе [15]. Для нового примитива возможность контакта определяется следующим образом.

Обнаружение контакта двух ЦСТ, имеющих радиусы R ₁ и R ₂, основано на расчете минимального расстояния d ^min между их центральными отрезками по алгоритму, описанному в работе [16]. Контакт имеет место, если d ^min<  R ₁ + R ₂.

При обнаружении контакта ЦСТ, задаваемого концами A ₁, A ₂ центрального отрезка и радиусом R , с плоскостью P учитывается, что координаты A ₁, A ₂ определяются в расположенной на плоскости СК с началом в точке О и осью Х , направленной в сторону, обратную внедрению ∆ в эту плоскость (рис. 6). Поэтому контакт имеет место, если абсцисса хотя бы одного из концов ЦСТ меньше величины радиуса R .

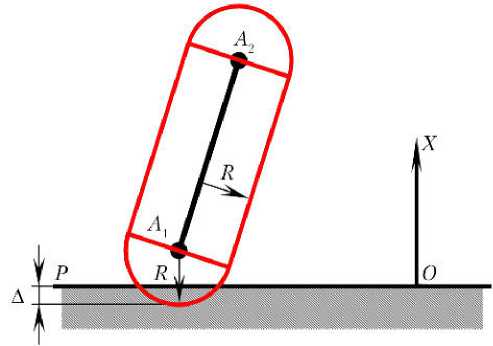
Рис. 6. Обнаружение контактов цилиндра со сферическими торцами с плоскостью