Выбор параметров симметрирующего устройства в зависимости от изменяющихся показателей несимметрии в распределительных сетях 0,38 кВ с сосредоточенной нагрузкой

Несимметрия токов вызывает появление тока в нулевом проводе, а вместе с тем и напряжения смещения нейтральной точки системы фазных напряжений. В результате напряжения фазы на зажимах электроприемников становятся несимметричными. Несимметрия напряжений, как следствие несимметрии токов, оказывает отрицательное влияние на электрооборудование. В частности, это ухудшает работу конденсаторных установок, оказывает отрицательное воздействие на работу защиты установок, приводит к существенным ошибкам при учёте электроэнергии, ухудшает работу электрических двигателей. Несимметрия токов является также причиной появления добавочных потерь мощности, что является одной из причин теплового повреждения изоляции. Кроме того, несимметрия токов обусловливает магнитное влияние линий 0,38 кВ на проходящие вблизи линии связи. Среди основных последствий появления несимметрии токов можно также назвать снижение надежности системы электроснабжения.

Наиболее эффективным средством снижения несимметрии токов является применение симметрирующего устройства с минимальным сопротивлением нулевой последовательности. Существующие методы определения симметричных составляющих основаны на законах параметров изменяющейся нагрузки и заранее заданных параметров симметрирующего устройства.

Цель исследований . Определение параметров симметрирующего устройства для любого вида несимметрии в зависимости от заданных параметров нагрузки и показателей несимметрии.

Результаты исследований и их обсуждение . Основываясь на методе симметричных составляющих, система уравнений для токов будет выглядеть следующим образом:

f La — b. + Б + b'> \Lb — а² • L . + а • L 2 + L o ; \Lc ^— a • ^ + a ² • Ь + Ь,

где La,Lb,L: - токи соответственно фаз А, В, С; L i ,Ь,L o - токи соответственно прямой, обратной и нулевой последовательности; а - оператор поворота или фазный множитель (а — е ²²/ ^{3 3} — е~²⁴/ ^{3 3} — - . + i у).

Аналогичные соотношения можно получить для симметричных составляющих прямой, обратной и нулевой последовательностей напряжений:

Is

[^ — и . + 1^ + 1^;

— а² • U . + а • U + + Uq ;

— а^ U . + а ² -U+ + U,

Рассмотрим случай, когда узел нагрузки состоит из трёхфазных симметричных электроприёмников, включенных на междуфазное напряжение, образующих трёхфазную симметричную нагрузку, и однофазных электроприемников, включенных на фазное напряжение и образующих трехфазную несимметричную нагрузку. Предположим, что симметрирующее устройство включено непосредственно в узле нагрузки. Схема электроснабжения такого узла представлена на рис. 1.

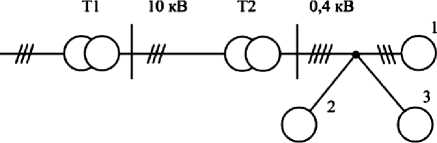
Рис. 1. Схема участка электрической сети с нагрузками и симметрирующим устройством:

1 – S s – полная мощность трехфазной симметричной нагрузки; 2 – S су – полная мощность симметрирующего устройства; 3 – S н – полная мощность трехфазной несимметричной нагрузки

Изобразим схему замещения для данной трёхфазной сети (рис. 2).

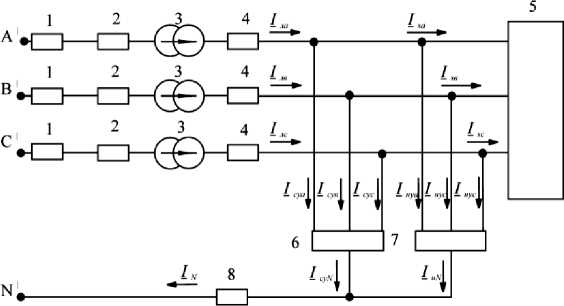
Рис. 2. Схема замещения участка электрической сети с нагрузками и симметрирующим устройством:

^{1 -} ? ЛВ 1 ; ^{2 -} ^ J i ^— Z j 2 ^; Z_ T 0 ; ^{3 -} Ц ; ^{4 -} ^H i ^— ^H 2 ^; ^H O ; ^{5 -} ?s l^; ?s 2^; ? sO ^{— М} ; ^{6 -} ? су 1 ^— ? су 2 ^; ? су О ;

^{7 -} ^ н ! ^— Z _H 2 ^; ^ н П ; ^{8 -}

Приняв фазу А за основную и заменив трёхфазную несимметричную нагрузку тремя источниками неизвестных напряжений U_Ha, U_Hb, U_HC , разложим эти напряжения на симметричные составляющие напряжений прямой U _{H i} , обратной U _{H 2} и нулевой и_нп последовательностей. В результате получим симметричную трёхфазную сеть, схема которой изображена на рис. 3.

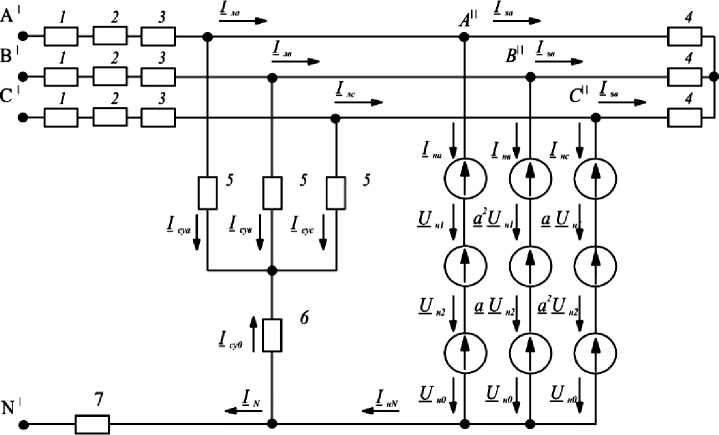
Рис. 3. Схема замещения участка электрической сети с трехфазным несимметричным источником напряжения и приведенными параметрами к сети напряжению 0,38 кВ:

1 –z ' _{лв г} =   ' _{лв 2} ; 2 –z ' _Т , =   ' _{Т 2}, Z ' _{Т 0}; 3 –Z лн 1=   лн 2, Z лн 0 ; 4 – Zsi , Zs2 ; 5 –Z су 1=   су 2 ; 6 –Z су о ; 7 – Zj

Проводимости симметрирующего устройства фаз А, В и С определяются следующими выражениями:

у _ I суА   у _ I суВ Y _ I суС

-суА⁼ U н ^у А ^; - суВ ⁼ и нВ ^; -суА⁼ U нС

где I_{суА , В , С} – ток в фазах А, В и С соответственно симметрирующего устройства, А; U_{нА , В , С} – напряжение фаз А, В и С соответственно.

Токи в фазах симметрирующего устройства можно представить с помощью симметричных составляющих:

{     су A = су 1⁺ L су 2⁺ / су 0^;

I су В =    _∙ L су i⁺ a ^∙ I су 2⁺ L су 0^;

/ суc =    ^∙ L су i⁺ H _∙ I су 2⁺ I су 0^,

где токи 7 су 1 , 1 су 2 , 1 су Q – это токи прямой, обратной и нулевой последовательностей и вычисляются они из следующих выражений:

{ су 1= су 1∙1 су 1; l су2= су 2∙I су 2;

I су 0=    су 0^∙I су 0^․

По исходной схеме и суА = инА , и суВ = инВ , и суС = и_нС , поэтому симметричные составляющие этих напряжений также должны быть равны соответственно.

Таким образом, подставляя выражение (5) в формулы (4) и учитывая равенства напряжений, получим:

г    LсуА= н ∙X су 1+ и. н ∙X су 2+ино∙X су о; су В=    ∙ин ∙X су 1+И∙ У. н  ∙X су2+ IX но∙X су о;

XLсу с =    ^∙ LL н ^∙ X су 1+ «^{2 ∙} LL н  ^∙ X су 2 + LL н о^∙ X су о^․

Полученные выражения (6) подставляем в формулу (3):

У су ⁼

и н ∙ 2 су 1 + и н ^∙ X су 2 + U н О ^∙ X су о ин ⁺ ин + ин о

Ц^{2 ∙} ^ н ^∙ X су 1 + ^ ^∙ и н ^∙ X су 2 + и н О ^∙ X су О

су ^{В =}             ∙ ин + а ∙ Uн ⁺ Uн о         ^;

= ∙ ^н ∙2 су 1+    ∙ н ∙I су 2+ ^нО∙I су О а∙Uн + а2 ∙Uн +ин0

В выражении (7) неизвестными для нас величинами при заданных исходных данных, а именно напряжении и сопротивлениях всех элементов схемы, остаются сопротивления симметрирующего устройства. Для этого произведем дальнейшие преобразования, представленные на рис. 4.

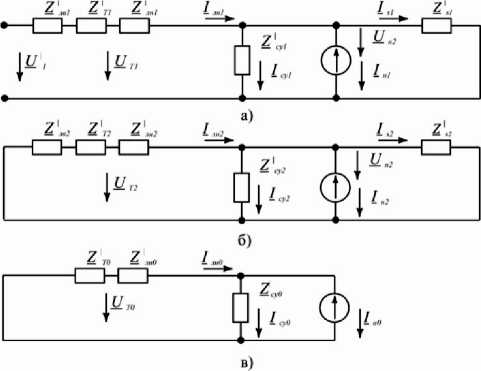
Рис. 4. Схемы прямой (а), обратной (б) и нулевой последовательностей (в) для основной фазы трехфазной симметричной цепи с симметрирующим устройством

В схеме прямой последовательности заменим активную и две пассивные параллельные ветви одной эквивалентной ветвью с источником напряжения U_э 1 и проводимостью У _э ^:

ь^∙ и '

иэ 1⁼ — Y ^; Xэ =   ⁺ bi ^․

+ Lpi

В выражении (3):

+ 2 ' _{Т г}+ 2 лн i^,

где Xpi = су 1 + bl – суммарная комплексная проводимость прямой последовательности симметрирующего устройства и трёхфазной симметричной нагрузки.

В схеме обратной последовательности (рис. 4, б) заменим три пассивные параллельные ветви одной эквивалентной ветвью с проводимостью э2=   + b2 ․

В выражении (9):

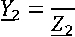
где z_? = ' + z ' + z лн 2; 1^2 = су 2+ 1^2 – суммарная комплексная проводимость обратной последовательности симметрирующего устройства и трёхфазной симметричной нагрузки.

В схеме нулевой последовательности (рис. 4, в ) заменим две пассивные параллельные ветви одной эквивалентной ветвью с проводимостью

В выражении (11):

Y э о= су 0+ Zo ․

, где ^0 =  'Т 0+2 лн 0․

После проведённых преобразований схем (рис. 4) получим одноконтурные расчётные схемы замещения прямой, обратной и нулевой последовательностей, изображённые на рис. 5.

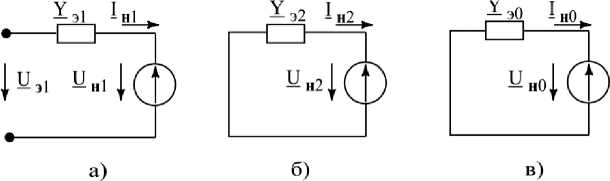
Рис. 5. Эквивалентные схемы прямой (а), обратной (б) и нулевой (в) последовательностей

Для схем прямой, обратной и нулевой последовательностей (рис. 5) составим по второму закону Кирхгофа следующие уравнения:

^н - + U н  = э ; = ^н - + н

J 4 1                        I 4 2

=0; ^{н 2}+ U н0 =0․

Lэ о

С учетом исходной схемы и параметров трехфазной цепи:

U =_Ү ( І н1+ І _н2 + І _н0);

■ U В =_Ү( а ² ∙ І _н1+ а ∙ І _н2 + І _н0 );

⎪1                  2

^⎪ U С = _Ү ( а ∙ І н1 + а

∙ І _н2 + І _н0)․

⎩      Ү С

Подставив уравнения (13) в систему (14), получим:

_⎪ ⎧ Ү ₁ (( U э ‘ - U н ■ )∙ Ү э - U н ■ ∙ Ү э - U н ■ ∙ Ү э • )= U

( а ²∙( U э1 - U _н 1 )∙ Ү э - а ∙ U н2 ∙ Ү э - U н0 ∙ Ү э0 )= U В                (15)

^{⎪ 1} ( а ∙( U э1 - U _н1 )∙ Ү э ^{- а 2} ∙ U н2 ∙ Ү _э - U _н0 ∙ Ү _э0 )= U В ․

⎩ Ү С

Таким образом, после некоторых преобразований, получаем следующую систему уравнений:

( U э - U н ) ∙    - U н         U н ⎧     Ү     ∙ Ү э - Ү ∙ Ү э - Ү ∙	Ү э О = U
⎪ а ∙(U э -U н ) ∙    - а ∙ U н Ү       ∙ Ү э - Ү   ∙ Ү э	- Ү J ∙ Ү э О = U в
⎪ а∙(U э -U н ) ∙   - а ∙U н ⎩ Ү   н ∙ Ү э -   Ү н ∙ Ү э	- Uн 2 ∙ Ү э О = U с․ Ү с

Систему уравнений (16) решим методом Крамера. Данный метод основывается на последовательном вычислении (n+1) определителей матрицы, имеющей размерность (nxn).

Главный определитель системы уравнений:

3∙ а ∙( U э1

	( U э 1 - U н1)	U н 2	U н 0 1
	Ү	Ү	- Ү
	а 2∙( U э1 - U н1)	а ∙ U н2	U н 0
=
	Ү	Ү	Ү
	а ∙( U э1 - U н1)	а 2 ∙ U н2	U нО
	Ү с	Ү С	Ү с
- U н 1	)∙ U н2 ∙ U нО-3∙	а 2∙( U э1-	U н 1)∙ U	н2

∙ U но

3∙(Uэ 1 -U_н 1 )∙Uн 2 ∙Uн О Ү∙Ү∙Ү

∙( а - а ² )․

Далее найдем дополнительные определители системы Δ 1 , Δ 2, Δ 2.

U н2 ∙ U н О

Ү ∙ Ү В ∙ Ү С

U н2 ∙ U н О Ү ∙ Ү В ∙ Ү С

| Δ =	U     - U Ү н :    - U Ү н ’ 1 U   - а ∙ U н2   - Uн - U ҮҮ а 2 ∙U     U н           н
	U - Ү С  - Ү с
U ∙ Ү ∙(	а- а 2)+ U В∙ Ү ∙( а 2-	1)+ U с ∙ Ү с∙(1- а ))-

∙( U ∙ Ү + а ∙ U В∙ Ү + а ² ∙ U с ∙ Ү с)∙( а - а ²)․

(U э 1 -U _н 1 )∙U н о Ү ∙ Ү ∙ Ү с

(U э 1 -U _н 1 )∙U н о Ү∙Ү∙Ү

	( U э 1 - U н1)	U	U н °|
	Ү		- Ү
Δ =	а 2 ∙( U э1 - U н1)	U в	U н 0
	Ү		Ү
	а∙(Uэ 1 -Uн 1 )	U с	U н О
	Ү с		Ү с 1

∙( U ∙ Ү ∙( а ²- а )+ U в∙ Ү ∙( а -1)+ U с ∙ Ү с∙(1- а ² ))

∙(- U ∙ Ү - а ² ∙ U в ∙ Ү - а ∙ U с ∙ Ү с)∙( а - а ²)

( U э 1 - U н1)	U н 2	U
Ү	Ү
а 2 ∙(Uэ 1 -Uн 1 ) Ү	а ∙ U н2 - Ү	U В
| а∙(Uэ 1 -Uн 1 ) Ү с	а 2 ∙Uн 2 - Ү С	U с

( U э 1- U _н 1)∙ U н2∙(- а ∙ U С ∙ Ү с - а ∙ U в∙ Ү - а ∙ U ∙ Ү + а ²∙ U ∙ Ү + а ² ∙ U в∙ Ү + а ² ∙ U с ∙ Ү с)

Ү ∙ Ү В ∙ Ү С ^{= (U э} Ү ^- ∙ Ү ^{U н 3} ∙ ⁾ Ү ^{∙U н} - ∙(- U ∙ Ү - U В∙ Ү - U с ∙ Ү с)∙( а - а ²)․

Далее определяем эквивалентные проводимости прямой, обратной и нулевой последовательностей из системы (16) через найденные определители.

Δi U ∙Ү +а∙U в ∙Ү+а ² ∙U с ∙Ү с ⁼ Δ ⁼         3∙( U э1 - U _н1) ^;

Δ2   (-U ∙Ү -а ² ∙U в ∙Ү -а∙U с ∙Ү с )

⁼ Δ ⁼             3∙ U н₂

Ү =^Δ3  (- U ∙ Ү - U в∙ Ү - U с ∙ Ү с)

Ү э ° ⁼ Δ ⁼            3∙ U н ;           ․

Таким образом, получив формулы для нахождения эквивалентных проводимостей прямой, обратной и нулевой последовательностей, с помощью формул (8)–(12) можно найти требуемые проводимости симметрирующего устройства по формуле. Проводимости симметрирующего устройства прямой, обратной и нулевой последовательностей можно найти по следующей формуле:

^Ү су 1 { ^Ү су2

Ү суО

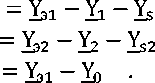
Благодаря полученной системе уравнений (18), можно определить параметры симметрирующего устройства в зависимости уровня несимметрии токов и напряжений исследуемой сети.

Так как мы исследуем вполне реальную систему, напряжения и токи прямой, обратной и нулевой последовательностей можно найти через коэффициенты несимметрии напряжений и токов соответственно для каждой последовательности. Поэтому с помощью формул (19)–(24) можно определить недостающие величины [2, 3].

- Напряжение прямой последовательности :

U а

U н ^{1 =} 1+ К ^а + К

-2ин   —Ouн

․

- Напряжение обратной последовательности :

U н 2 = U н1

∙

К ․

-2ин․

- Напряжение нулевой последовательности :

U нО = U нi      ^․

—ни   —Hl _QUH

- Ток прямой последовательности :

І _н ⁼

І _а

1+ К + К ^․

—21н   —Oiн

- Ток обратной последовательности :

І н ² = І н¹∙ К 2iн ^․

- Ток нулевой последовательности :

І н О = І н¹∙ К Oiн ^․

В формулах (19)–(24) К _н , К _н , К , К – коэффициенты несимметрии напряжений и токов соответственно индексам u и і по о^нбратн^ной и^ннуле^нвой последовательностям [3]. Пример расчета параметров симметрирующего устройства в распределительной сети 0,38 кВ. Для приведенного выше метода расчета параметров симметрирующего устройства, выполним расчет на примере схемы на рис. 1. Расчёт был произведён при следующих исходных данных. Проведённые расчёты потерь мощности и показателей несиммет-рии токов и напряжений в сети 0,38 кВ без симметрирующего устройства показали, что при среднем значении статистической несимметрии напряжений на зажимах электроприёмников, составляющей 7,3 %, несим-метрия вторичных напряжений трансформатора распределительной подстанции 35/10 кВ не превышает 2 %. Поэтому в расчётах показателей несимметрии токов и напряжений и потерь мощности в качестве условно симметричного источника питания можно принимать распределительную подстанцию 35/10 кВ.

Длина ВЛ 10 кВ взята по нормам надёжности электроснабжения, равная 16,7 км. Комплексное сопротивление прямой (обратной) последовательности этой линии, выполненной проводом марки АС-35, приведено к напряжению 0,4 кВ:

Ζ лв i = Ζ _лв2 =0,0243+ј0,01=0,0263∙ еj22 ^, 45 ° Ом.

Питание нагрузки осуществляется от потребительской подстанции ТП 10/0,4 кВ с трансформатором со схемой соединения обмоток “звезда-звезда с нулём” мощностью Ѕ _ном =40 кВА. Сопротивление прямой (обратной) последовательности трансформатора:

Ζ т i = Ζ т₂ =0,09+ј0,156=0,18∙еj60 ^, 02 ^° Ом․

Комплексное сопротивление нулевой последовательности трансформатора:

Ζ т0 =1,133+ј1,73=2,068∙ еj56 ^, 78 ^° Ом ․

Длина ВЛ 0,38 кВ составляет 0,5 км; линия выполнена проводом марки 4А-50. Сечение фазных и нулевого проводов приняты одинаковыми. Комплексные сопротивления прямой (обратной) последовательностей линии 0,38 кВ равны:

^Ζ лн i = Ζ лн₂ =0,315+ј0,148=0,348∙ еj25 ^, 24 ^° Ом ;

^Ζ лн0 =1,26+ј0,47=1,345∙ еj20 ^, 46 ^° Ом ․

Узел нагрузки в конце ВЛ 0,38 кВ содержит трёхфазные симметричные электроприёмники – асинхронные электродвигатели общей мощностью Ѕ_sс cοs φ =0,8 и однофазные электроприёмники мощностью Ѕ _н с cοsφ = 0,9 , неравномерно распределённые по трём фазам.

Методика применима для различных соотношений мощностей Ѕ_s и Ѕ_н при номинальной мощности трансформатора, т.е. соблюдено следующее условие:

рs +рн = const, s s s где рн=ра+рв+рс= Г а+ в+Гс․ ном   ^ном   ^ном

Полные мощности и комплексы проводимостей отдельных фаз трёхфазных симметричной и несимметричной нагрузок определены на основании статистических характеристик несимметрии токов в сельской сети по аналитическим выражениям в соответствии с [1, 2].

Относительные значения мощностей симметричной и несимметричной нагрузок изменяются в соответствии с таблицей.

Относительные значения мощностей трёхфазных симметричной и несимметричной нагрузок

ра	рв	рс	рs 1
0,0177	0,00425	0,003	0,225

Углы сдвига фаз трёхфазных симметричной и несимметричной нагрузок приняты в соответствии со среднестатистическими данными несимметрии токов в сетях и соответственно равны [1]:

φs = 36,87°; φa=φb =φc = 25,84°․

Основываясь на расчетах [1,2], значения коэффициентов несимметрии примем следующие:

Κ 2uн =0,00237∙еj217 ^, 9745 ^° = -0,0019 - ј0,0015;

Κ Ou^нн =0,03329∙еj254 ^, 5942^° = -0,0088 - ј0,0321;

Κ 2iл=0,03065∙еj27 ^, 3581 ^° = 0,0272 + ј0,0141;

Κ Oi^лл =0,05192∙еj20 ^, 8342^° =0,0485+ј0,0185․

Расчет начнем с нахождения напряжений фаз А, В и С через их составляющие прямой, обратной и нулевой последовательностей, найденные в свою очередь через имеющиеся коэффициенты несимметрии.

Uн i =      Uа      =222,2447∙еjl, 945°=222,1166+ј7,543; н =1+К2uн+КOuн

U н₂ = U нi∙ К 2uн =0,5267∙еj219 ^, 92^°=-0,4039-ј0,3379;

U н О = U н i ∙ К Ou н ^н=7,3985∙еj256 ^, 539^° =-1,7223-ј7,1953․

Таким образом, фазные напряжения будут равны:

U = U н i + U н₂ + U н О = 219,9904 + ј0,0098 = 219,9904 ∙ еjo ^, 0026 ^° В; U В = а ² ∙ U н i + а ∙ U _н2 + U н0 = -105,7535 - ј203,5063 = 229,4336 ∙ е-jll7 ^, 4593 ^° В; U С= а ∙ U н i + а ² ∙ U ^нн₂ + U ^нн0 = -119,4038 + ј181,9107 = 217,5977 ∙ еjl23 ^, 2804 ^° В․

Далее рассчитаем комплексные проводимости трехфазных несимметричной нагрузки:

Ү

^Ү Si = Ү

Ѕ ном ∙р_a    40000 ∙ 0,0177

Ү

Uф․ном ∙е]Фа = 220 2∙ 1 Ѕном ∙ рb 40000 ∙ Uф․ном ∙ еj

еj25,84°

∙ 0,003 еj25,84°

=0,0146∙е425 , 84 ° См;

=0,0035∙е425 , 84 ° См;

=0,0025∙е425 , 84 ° См;

Үэ 1 =Үэ

ЅI

Uл․ном ∙ е j=3802 ∙еj36 ^, 87 ^°

Ү +а∙UВ∙Ү+а² ∙Uc∙Үc

=0,0623∙е -j36 , 87°=0,0498-ј0,0374 См;

3∙(Uэ1

-

Uн 1)

=0,0875∙еjl50 , 8342 ° = -0,0764 + ј0,0426 См;

Үэ О=_∙          ∙Ү^с-⁾=0,1152∙еJ148 ^, 3617^°=-0,0981+ј0,0604 См․

3∙U_нО

Проводимость прямой, обратной и нулевой последовательностей:

Ү =   =                  =1,8801∙е-J36 ^, 1826^°=1,5175-ј1,1099 См;

Ζ      лв ; +Ζ_Τ ; +Ζ_лн     ,       е              ,        ј,       м;

Ү=Ү;

Ү =   =           =0,3076∙е-J42 ^, 5938^° =0,2264-ј 0,2082 См․

_Ζо   Ζ′_То +Ζ_лн      ^{,                        ,            ,}

Үсу i =Үсу₂=Үэi-Ү-ҮSi =-1,6437+ј1,1899=2,0292∙еjl44 ^, 0986 ^° См;

• ^Үсу О ₌ с_Үу_э О-Ү^су=-0^э,3245+ј0,2686=0,4212∙еjl40 ^, 3843 ^° См․

Заключение. Получив экспериментальным путем данные по несимметрии токов и напряжений на заданном участке действующей сети 0,38 кВ, с помощью формулы (18), можно определить необходимость применения симметрирующего устройства, а также его параметры для каждого конкретного участка этой сети.