Выбор порога чувствительности для систем диагностики

По мере накопления и расширения знаний об окружающем мире все актуальней становятся задачи диагностики в различных областях человеческой деятельности: техника, медицина, экономика и д.р. По своей сути диагностика – это процесс установления диагноза или распознавания проблемы. В процессе диагностики проводится сравнение текущего состояния объекта исследования с его моделью. Если совпадение оказывается неудовлетворительным, выдается предупре- ждающее сообщение, инициирующее предусмотренные действия. Своевременная диагностика нежелательных событий позволяет минимизировать затраты, связанные с лавинообразным накоплением нарушений в сложных системах. Безусловно, к сложным системам относятся и атомные станции, для которых эффективным признается использование диагностических средств, позволяющих быстро обнаруживать симптомы отказов и ухудшение рабочих характеристик, что непосредственным образом связано с повышением безопасности, надежности и экономической эффективности эксплуатации АЭС и ядерной энергетики в целом.

1 – Национальный исследовательский ядерный университет «МИФИ».

внутриреакторного контроля и своевременного выявление отказов оборудования и ошибок в исходных данных программ сопровождения эксплуатации ЯЭУ [1, 2, 3].

Однако, как это часто бывает, если программа не является достоянием сообщества людей, которое непрерывно бы поддерживало и совершенствовало ее работоспособность, то программа устаревает и через какое-то время становится неработоспособной. К сожалению, такая судьба постигла и ПС непрерывной диагностики ECRAN.

Тем не менее реализованные в программе алгоритмы не были утеряны, а возможность живого контакта с авторами и разработчиками позволила восстановить заложенный в программу научный потенциал. Использование современных кодов, методов и подходов к разработке программного обеспечения позволило вдохнуть в программу новую жизнь, сделало ее код работоспособным под современными операционными системами на современной компьютерной технике. Проведенные усовершенствования диагностических алгоритмов позволили повысить их точность и скорость работы.

Таким образом, была создана расчетно-измерительная диагностическая система ECRAN 3D [4 – 8], основу которой составляют аттестованные программные средства сопровождения эксплуатации (POLARIS [9], КОНТУР-М [10]), а также апробированные методы обработки экспериментально-расчетной информации о состоянии активной зоны и базы данных РБМК.

Однако при работе любой системы диагностики могут возникать ошибки первого и второго рода. Ошибки первого рода и ошибки второго рода в математической статистике – это ключевые понятия задач проверки статистических гипотез. Тем не менее данные понятия часто используются и в других областях, когда речь идет о принятии «бинарного» решения (да/нет) на основе некоего критерия (теста, проверки, измерения), который с некоторой вероятностью может давать ложный результат.

Пусть дана выборка X = (X₁,...,X_n)^T из неизвестного совместного распределения P^X , и поставлена бинарная задача проверки статистических гипотез: H₀ ,

H₁ , где H₀ – нулевая гипотеза, а H₁ – альтернативная гипотеза. Предположим, что задан статистический критерий:

f : R n → {H 0 , H 1 } , сопоставляющий каждой реализации выборки X = x одну из имеющихся гипотез. Тогда возможны следующие четыре ситуации.

• 1    Распределение P^X выборки X соответствует гипотезе H₀ , и она точно определена статистическим критерием, то есть f(x) = H₀ .

• 2    Распределение P^X выборки X соответствует гипотезе H₀ , но она неверно отвергнута статистическим критерием, то есть f(x) = H₁ .

• 3    Распределение P^X выборки X соответствует гипотезе H₁ , и она точно определена статистическим критерием, то есть f(x) = H₁ .

• 4    Распределение P^X выборки X соответствует гипотезе H₁ , но она неверно отвергнута статистическим критерием, то есть f(x) = H₀ .

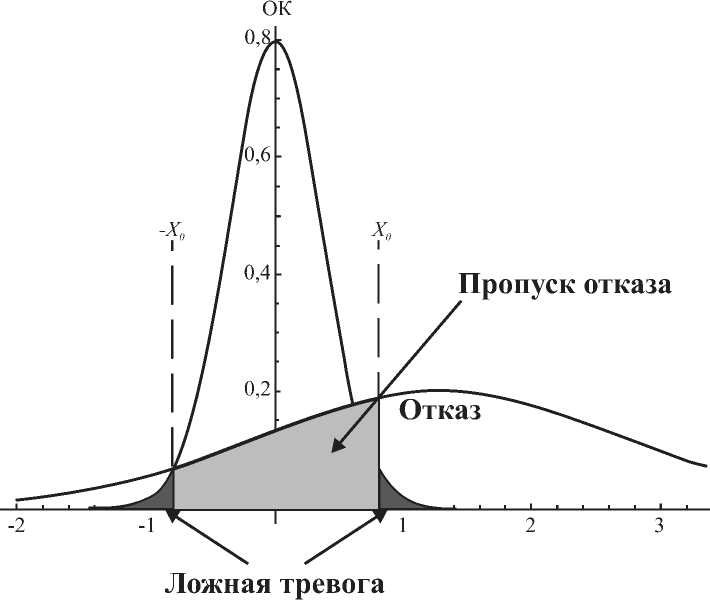
Во втором и четвертом случае говорят, что произошла статистическая ошибка, и ее называют ошибкой первого и второго рода соответственно. Пропуск отказа при его фактическом наличии назовем ошибкой первого рода. Регистрацию отказа при его отсутствии назовем ошибкой второго рода.

Как видно из вышеприведенного определения, ошибки первого и второго рода являются взаимно симметричными, то есть, если поменять местами гипотезы H0 и H1, то ошибки первого рода превратятся в ошибки второго рода и наоборот. Тем не менее в большинстве практических ситуаций путаницы не происходит, поскольку принято считать, что нулевая гипотеза H0 соответствует состоянию «по умолчанию» (естественному, наиболее ожидаемому положению вещей) – например, что исследуемый объект находится в работоспособном состоянии. Соответственно альтернативная гипотеза H1 обозначает противоположную ситуацию, которая обычно трактуется как менее вероятная, неординарная, требующая какой-либо реакции. С учетом этого ошибку первого рода часто называют ложной тревогой, ложным срабатыванием или ложноположительным срабатыванием – например, анализ положения регулирующего органа показал его обрыв, хотя на самом деле обрыва не произошло. Из-за возможности ложных срабатываний не удается полностью автоматизировать борьбу со многими видами ошибок. Как правило, вероятность ложного срабатывания взаимосвязана с вероятностью пропуска события (ошибки второго рода). То есть, чем более чувствительна система, тем больше опасных событий она детектирует и, следовательно, предотвращает. Но при повышении чувствительности неизбежно вырастает и вероятность ложных срабатываний. Поэтому чересчур чувствительно (параноидально) настроенная система диагностики может выродиться в свою противоположность и привести к тому, что побочный вред от нее будет превышать пользу. Соответственно ошибку второго рода иногда называют пропуском события или ложноотрицательным срабатыванием – объект не работоспособен, но анализ состояния этого не показал. Степень чувствительности системы защиты должна представлять собой компромисс между вероятностью ошибок первого и второго рода. Где именно находится точка баланса, зависит от оценки рисков обоих видов ошибок [11].

Экономический подход к принятию решения

Во время работы системы диагностики обычно приходится идти на компромисс между приемлемым уровнем ошибок первого и второго рода. Зачастую для принятия решения используется пороговое значение, которое может варьироваться с целью сделать тест более строгим или, наоборот, более мягким. Этим пороговым значением является уровень наличия отказа, которым задаются при проверке статистических гипотез.

Возможны разные подходы к оценке рисков обоих видов, а соответственно и к выбору уровня наличия отказа. Опишем один из них – экономический. Для этого выберем порог принятия решения так, чтобы минимизировать средний ущерб при эксплуатации системы.

Теперь рассмотрим модель работы диагностической системы. Диагностическая система работает, производя

периодические проверки с заданным шагом по времени dt . Если выходной сигнал для данного типа отказа превышает заданный порог, происходит принятие решения о наличии отказа. Также возможна альтернатива – принятие решения после N превышений порога подряд. После этого происходит проверка наличия отказа дополнительными средствами. При наличии отказа он устраняется мгновенно, с точки зрения системы диагностики.

Примем следующую модель шумов при нормальной эксплуатации системы:

- xL

Pok (x) = 777т e   2,

UN 2 Л причем отсутствуют корреляции по времени.

Модель отказов такова – отказы случаются с заданной равномерной плотностью по времени P_f . Плотность распределения в условиях наличия отказа тоже нормальна, но с другим законом:

P,(x)=

O_f al V2 ^

^(x-x 0 )²

–

e 2 ^

т.е. при появлении отказа возникает смещение и изменяется дисперсия сигнала оценки ошибки. В этих данных также отсутствуют корреляции.

Модель ущерба

Таблица 1. Ущерб в различных ситуациях

Величина	Отказ есть	Отказ зарегистрирован
0	0	0
check	0	1
C fail + C check + Crepare	1	0
f(t) ·Cfail + Ccheck + Crepare	1	1

В таблице 1:

• ♦    C check — стоимость проведения проверки на наличие отказа;

• ♦    C repare — стоимость ремонта;

• ♦    C fail — асимптотическая стоимость ремонта, вызванная несвоевременным обнаружением отказа;

• ♦    f(t) характеризует нарастание последствий при работе без принятия мер по ремонту, она равна нулю при t = 0 и равна 1 при t → ∞ .

В дальнейшем будем пренебрегать C_check + C_repare по сравнению с членом C fail .

Работа диагностической системы имеет смысл, если она позволяет обнаружить отказ на начальных этапах нарастания стоимости последствий. Чтобы упростить рассмотрение примем, что темп нарастания последствий невелик по сравнению с временным окном усреднения по времени в алгоритме поиска отказа. Тогда можно заменить: f(t) × C_fail → C_fail.

Рис. 1. Оценка вероятностей ошибок первого и второго рода

Посчитаем ущерб как функцию порога принятия решения о наличии отказа в предположении, что отказы – редкое явление.

Для дальнейших выкладок нам потребуется соотношение:

| 12

erfc ⎜ σ⎟             ∞

V V ¹ I и, ----т=— =         e ^{V V} dx .

2 V 2

Для упрощения примем экспоненциальную модель нарастания стоимости последствий отказа:

f(t) = 1 – e –λt.

Пусть вероятность нахождения в состоянии отказа равна Pf, а уровень тре- вог ξ. Тогда компонента стоимости С2, связанная с ложными тревогами, с учетом двухсторонних ограничений будет иметь вид:

.

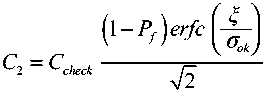
Обозначим вероятности ошибки первого рода P₁ , а вероятность ошибки второго рода P₂ :

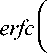
^x о + ^ fail ⎠

+ erfc

$ ^{- x} 0

fail

P i =

2V2

P 2 = 1 – P 1 .

Тогда средняя стоимость последствий отказа С₁ будет иметь вид:

( - 1 + e dt ) P

,

C1 Cffed* -P1 )(1 - P1)

а средняя стоимость С₂ , связанная с ложными тревогами:

TO

C2 = Cfaii • PflS (1 - e-lidt )• P1i I • i=1

Таким образом, изменяя ξ необходимо минимизировать функционал C₁ + C₂ , что легко осуществляется численными алгоритмами минимизации.

Заключение

В статье был изложен экономический подход, позволяющий выбирать порог чувствительности диагностических систем таким образом, чтобы минимизировать средний экономический ущерб при эксплуатации системы. Предложенный подход был применен для выбора порога чувствительности в системе ECRAN 3D, предназначенной для диагностики и мониторинга состояния активных зон и баз данных реакторов РБМК-1000. Проведенная расчетно-экспериментальная верификация созданного программного средства показала, что обеспечен требуемый уровень функционально-технических показателей системы диагностики