Выбор последовательности шагов для алгоритма сортировки Шелла

Автор: Сычв Птр Павлович

Журнал: Сетевое научное издание «Системный анализ в науке и образовании» @journal-sanse

Рубрика: Современные проблемы информатики и управления

Статья в выпуске: 1, 2023 года.

Бесплатный доступ

В работе приведены результаты эмпирического исследования нескольких последовательностей шагов для алгоритма сортировки Шелла. Показана достаточно высокая эффективность таких последовательностей в сравнении с другими, хорошо известными последовательностями.

Сортировка, сортировка шелла

Короткий адрес: https://sciup.org/14127897

IDR: 14127897

Текст научной статьи Выбор последовательности шагов для алгоритма сортировки Шелла

Sychov P. P. Choosing a sequence of steps for the Shell sorting algorithm. System analysis in science and education, 2023;(1):41–45 (in Russ). Available from:

Алгоритм сортировки Шелла ( ShellSort ) предложен в 1959 году [1] и занимает промежуточное положение между «медленными» алгоритмами сортировки с временной сложностью O(N²^, где N - размер сортируемого массива ( InsertSort , BubbleSort и т.д.) и «быстрыми» алгоритмами с временной сложностью O(NlogN) ( Quicksort, SortMerge и другие). Обычно временную сложность алгоритма ShellSort определяют как: O(N^K) где 1 < а< 2. Значение к зависит от выбора шагов алгоритма.

Алгоритм Шелла состоит в последовательном применении алгоритма сортировки вставками (InsertSort) с уменьшающемся шагом. Т.е. задается последовательность шагов (hm hm-1 … h1 ) такая что h1=1 и hk > hk-1. Массив, отсортированный с шагом p называется p-упорядоченным, т.е. все элементы этого массива, отстоящие друг от друга на расстояние, кратное p, упорядочены. Показано, что если р-упорядоченный массив отсортировать с шагом q, он останется p-упорядоченным, то есть он будет од- новременно и p и q-упорядоченным. Поэтому к последней сортировке с шагом 1 массив уже значительно упорядочен и сложность последнего этапа будет пропорциональна N, а общая сложность алгоритма – лучше, чем N2.

Хорошо изучены только некоторые последовательности шагов [2]. Генерация шагов можно производить либо по убыванию шагов, либо по их увеличению. Самый большой шаг должен быть сравним с размером массива, около N /2, чтобы на первом шаге сортировки в каждом подмножестве было только 2-3 элемента.

Методика

Для измерения характеристик различных последовательностей шагов была реализована функция сортировки массива целых чисел алгоритмом Шелла. Кроме массива чисел для сортировки в эту функцию передавался массив шагов, который использовался в алгоритме. Этот массив шагов готовился отдельно, в соответствии с выбранным алгоритмом генерации шагов, его размер зависел от размера сортируемого массива. Шаги располагаются в убывающем порядке.

Для каждого алгоритма генерации шагов сортировки генерировалось несколько массивов целых чисел разного размера, заполненных псевдослучайными значениями. Известно, что последовательность псевдослучайных чисел, генерируемых тем или иным генератором псевдослучайных чисел, полностью определяется начальным значением этого генератора. Чаще всего, в реальных программах, он инициируется текущим значением таймера, но его всегда можно задать явно. В нашем случае, для каждой серии прогонов использовалась одна и та же последовательность начальных значений.

Измерения

В таблице 1 приведены результаты тестовых прогонов программы для «медленных» последовательностей шагов. В первой строке приводится размер массива, в первом столбце – алгоритм генерации шагов. Элементы таблицы – усредненное по серии прогонов время работы функции сортировки для данного массива и данного набора шагов сортировки, округленное до целого числа миллисекунд.

Таблица 1. Результаты тестовых прогонов

Алгоритм	1000	2000	5000	10000	20000	50000	Линейный коэффициент
InsertSort	13	46	272	1092	4350	27131	1.97
h_k = 2^k	1	3	11	31	81	407	1.46
h_k = 3^k	1	3	11	36	77	262	1.46

Если временную сложность алгоритма ShellSort представить в виде t = CN^a , то логарифмируя это выражение получим logt = logC + alogN. Т.е. точки ( log t, log N ) должны аппроксимироваться прямой. Коэффициент ее наклона и будет представлять временную сложность в этом эксперименте. Коэффициент вычислялся по методу наименьших квадратов.

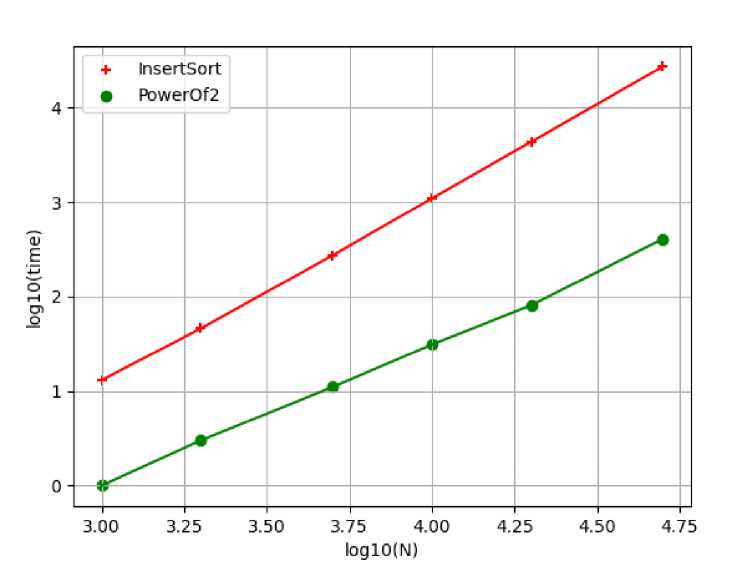
Рис. 1. График зависимости десятичного логарифма времени сортировки от размера массива

На рис. 1 приведен график зависимости десятичного логарифма времени сортировки от размера массива. Красный цвет соответствует обычной сортировке вставками, зеленый – последовательности шагов – степеней двух. График для последовательности шагов степеней трех не приводится, он практически совпадает с зеленым].

Временная сложность алгоритма сортировки вставками равна O(N²) , что согласуется с результатом в таблице 1. Средняя временная сложность для двух других алгоритмов тоже известна и равна 3

O(N 2 ) [2], что тоже соответствует результату в таб.1. Она относительно велика, так как последовательные шаги кратны друг другу, и при их использовании происходит слияние предыдущих подпоследовательностей, а не их перемешивание

Широко известные и часто используемые последовательности шагов приведены в таблице 2.

Таблица 2. Последовательности шагов

Алгоритм	10⁴	2 * 10⁴	5 * 10⁴	10⁵	2 * 10⁵	5 * 10⁵	10⁶	2 * 10⁶	Коэфф.
» к = 2 к	14	30	90	200	460	1372	3190	7071	1.18
N ^h k = 3 к	12	25	67	156	393	1084	2420	5504	1.17
Fibbo	16	35	100	230	541	1702	3902	8716	1.20
Sedgewick	10	22	60	131	270	731	1590	3363	1.09

Третий алгоритм в табл.2 – числа Фибоначчи, где очередной шаг равен сумме двух предыдущих, первые два равны 1 и 2.

Ряд нетривиальных последовательностей шагов предложено и изучено в работах [2,3,4]. Самой

лучшей, из известных на сегодня, является последовательность шагов, предложенная Седгевиком [4].

^ к

( 9 (2к( 8 • 2к —

+ 1, если к — четное

6 • 2(к+1)/2 + 1, если к нечетное

Средняя временная сложность для этой последовательности равна О(М б ) [4]. Результаты приведены в последней строке таблицы 2. На рисунке 2 приведены графики для последовательности 2 (на легенде графика – Div 3) и последовательности шагов Седгевика.

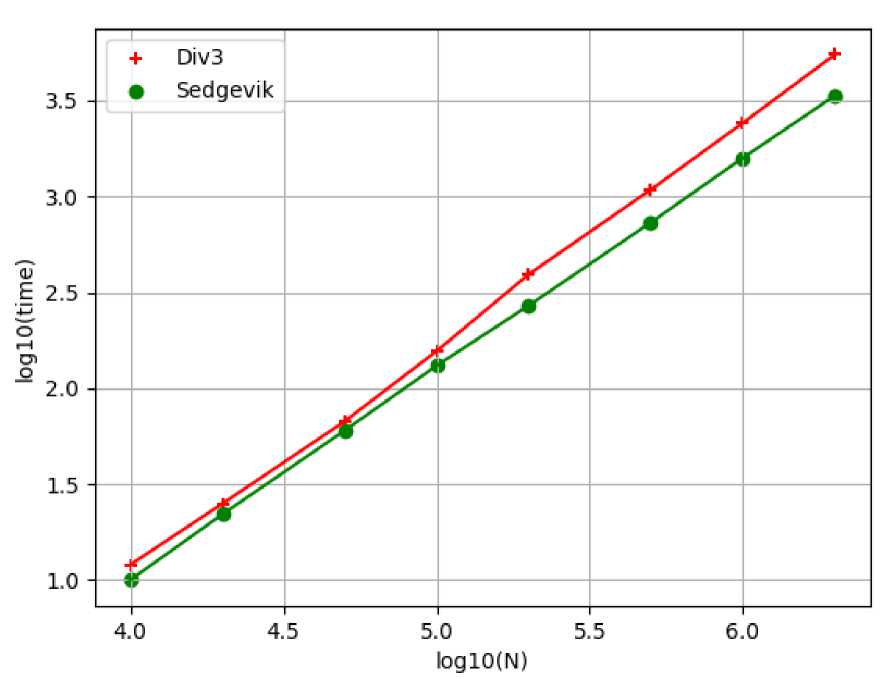
Рис. 2. Графики для последовательности 2

Рассмотрим последовательности, генерируемые формулой h_k+1 = L^h_kJ + 1, где a - некоторая действительная константа. Через L%J обозначена операция извлечения целой части числа. В таблице 3 приведены результаты прогонов для некоторых значений параметра а.

Таблица 3. Результаты прогонов

Параметр	10⁴	2 * 10⁴	5 * 10⁴	10⁵	2 * 10⁵	5 * 10⁵	10⁶	2 * 10⁶	Коэфф.
1.9	11	24	66	144	297	802	1738	3593	1.09
2.0	12	28	85	185	432	1267	2690	7192	1.17
2.1	10	22	61	132	283	754	1547	3356	1.09
2.3	9	20	59	127	282	743	1633	3387	1.09
2.5	10	22	60	130	271	736	1619	3421	1.10

Хорошо видно, что за исключением целочисленного значения a = 2, результаты вполне сравнимы с последовательностью Седгевика. График не приводится, так как эти линии почти сливаются.

Другая интересная последовательность шагов генерируется формулой h_k+1 = L^h_kJ. где a – некоторая действительная константа. В таблице 4 приведены результаты для этой последовательности при разных значениях параметра a.

Таблица 4. Результаты

Параметр	10⁴	2 * 10⁴	5 * 10⁴	10⁵	2 * 10⁵	5 * 10⁵	10⁶	2 * 10⁶	Коэфф.
2.1	11	24	65	138	287	784	1641	3515	1.09
2.3	10	22	63	134	289	771	1690	3511	1.09
2.5	10	23	62	135	283	787	1705	3638	1.11
2.7	11	22	61	127	274	755	1652	3447	1.09

И последняя серия шагов, порождаемая формулой h

k+i = ^", hi = — , где p, q - некоторые целые q 2

константы.

Таблица 5. Результаты

Параметры	10⁴	2 * 10⁴	5 * 10⁴	10⁵	2 * 10⁵	5 * 10⁵	10⁶	2* 10⁶	Коэфф.
p=13 q=31	10	22	60	132	282	750	1622	3544	1.09
p=15 q=31	11	23	62	135	286	754	1610	3418	1.09
p=17 q=31	11	24	68	138	297	785	1680	3551	1.09
p=19 q=31	12	25	68	146	302	847	1775	3752	1.10

Видно, что эти серии показывают очень неплохие результаты в рассмотренных условиях.

Результаты

Рассмотренные семейства шагов сортировки для алгоритма сортировки Шелла показывают хорошие результаты в практических тестах. Сами формулы для этих серий гораздо проще, чем, например, серия Седгевика. Однако, нужно отметить, что эти серии теоретически не изучены, и средняя сложность для них получена только эмпирически.

Список литературы Выбор последовательности шагов для алгоритма сортировки Шелла

Shell D. L. A high speed sorting procedure.Communications of the ACM. 1956. T. 2. № 7. С. 30-32.
Кнут, Д. Искусство программирования. Т 3: Сортировка и поиск. 3-е издание. Mосква: Вильямс, 2017.
Plaxton C. Greg, Suel Torsten. Lower Bounds for Shellsort. Journal of Algorithms. 1997. T. 23. № 2. C. 221-240.
Sedgewick R. A New Upper Bound for Shellsort. Journal of Algorithms. 1986. T. 7. № 2. С. 159-173.

Статья научная