Выбор рационального взаимного расположения несущих поверхностей экраноплана схемы "Утка"

Для каждого проектируемого летательного аппарата рациональность расположения несущих поверхностей (НП) определяется максимумом аэродинамического качества при соблюдении иных предъявляемых требований (условий технического задания и т. д.). Активно используются для этого численные методы (электронные продувки с использованием различных программных комплексов), продувки в аэродинамических трубах, буксировочные испытания в бассейнах и на открытой акватории. Однако используемые подходы для решения поставленной задачи приводят, фактически, к перебору вариантов взаимного расположения несущих поверхностей, что усложняет и удорожает процесс поиска решения, при значительном времени поиска. Аналитические методы существенно проще, но точность их существенно ниже, что не позволяет использовать их для решения подобных задач. Формирование нового подхода для определения рационального взаимного расположения НП экранопла-на схемы «утка» в сочетании с доработкой и интеграцией аналитических методов может позволить использовать последние для получения качественных результатов и, тем самым, существенно уменьшить число необходимых электронных продувок и экспериментов.

Для определения рационального взаимного расположения НП экраноплана схемы «утка» необходимо выполнение следующих задач:

1) определение поведения потока вблизи изолированной НП в зоне действия экранного эффекта:

– поведения потока за изолированной НП вблизи экрана;

– поведения потока перед изолированной НП вблизи экрана;

2) параметров потока в межкрыльевой области;

3) характеристик НП с учетом интерференции.

Для несущей поверхности вне экрана угол скоса потока считается определенным [1]:

c

s =     (1 + T),

n ■ К где т - коэффициент, учитывающий расстояние до НП, рассчитываемый по формуле

где L – расстояние по горизонтали от крыла до рассматриваемой точки А , лежащей в плоско сти сходящих вихрей; k – отношение размаха НП к расстоянию между свободными вихрями.

В инженерных расчетах угол скоса потока рассматривают в основном как функцию, определяемую коэффициентом подъемной силы и удлинения крыла ввиду малости значений коэффициента т .

Учет коэффициента т позволяет определить угол скоса потока в любой точке пелены, и, тем самым, определить ее траекторию.

Для моделирования экрана использован метод зеркального отражения (рис. 1), где h_a – отстояние рассматриваемой точки от экрана. При этом, для определения угла скоса потока в некоторой точке А , лежащей в плоскости вихревой пелены, необходимо учитывать также угол скоса, индуцируемый отраженной системой вихрей.

Для определения угла скоса потока принято относительное расстояни е от точки фокуса до рассматриваемой точки равным L . Начало координат находится в точке О , располагающейся между центрами давлений реальной и отраженной НП на экране. За положительное направление оси ОХ принято направление скорости набегающего потока U ₌ .

В результате выполнения необходимых преобразований, получена следующая зависимость:

( Л

2 пК

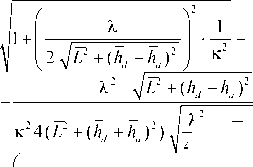
К

4к:

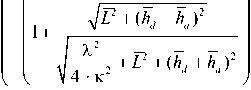
К

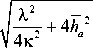
k ²

т = —

1 +

2 ■ L ^J k¹

где h_d – относительное отсто я ние точки центра давления НП по углу атаки от экрана; h_a – относительное отстояние вихревой пелены от экрана в рассматриваемой точке; к – коэффициент, определяемый по формуле:

к =

1+—

___ 2_X 1 - h

.

Таким образом, в свертке получим следующее:

y nV    экр) •

В формулу для определения угла скоса потока введена новая составляющая, отражающая, собственно, влияние экрана:

т экр

,             X2 V L 2 + ( К - h a. ) ²

+--1■ -

K ² 4( L + ( h d + h П     + L2 + ( h d + h_a ) ²

V 4к

XA

1+   УL2 + (hd - ha )2

1 1 ^{X +} L^{2 +} ( h d ⁺ h a ) ² K ²        + ⁴ h a²

Для решения использован метод максимальных приближений.

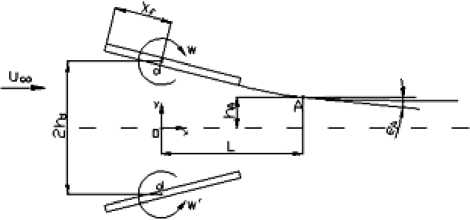
Рис. 1. Моделирование экрана методом зеркального отражения

Траектория вихревой пелены представлена состоящей из множества прямых отрезков. Пусть dL – элементар- ный горизонтальный отрезок, на котором вихревая пелена принимается движущейся прямолинейно (рис. 2). Угол скоса потока в i-й точке вихревой пелены имеет вид s,. = arctg

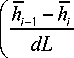
Для некоторой точки А, лежащей в плоскости вихре- вой пелены, используем формулу

n hA = hf -^ dL sin(s,_1),

= 1

где n – количество последовательно рассматриваемых точек при n –1 разбиении.

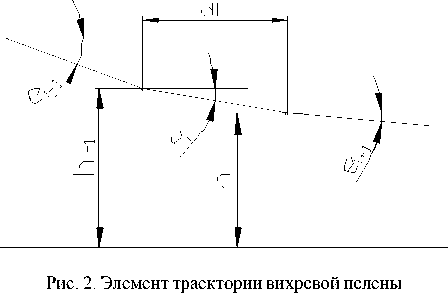
Определена траектория вихревой пелены за НП для различных значений удлинения НП, угла атаки и отстояния от экрана.

По представленным графикам (рис. 3, 4, 5) видно, что при увеличении угла атаки НП угол скоса потока пропорционально увеличивается; при приближении НП к экрану угол скоса потока уменьшается; при увеличении удлинения НП угол скоса потока уменьшается, что полностью согласуется с результатами исследований [2]. Кроме того, на расстоянии одной хорды от задней кромки НП поток условно можно принять горизонтальным ввиду малости значения угла скоса потока.

- 1.

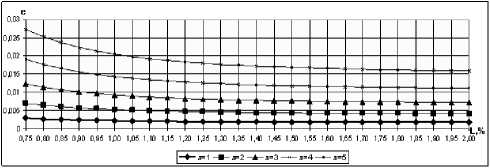
Рис. 3. Угол скоса потока при различных углах атаки при относительном отстоянии h = 0,1 и удлинении X = 2

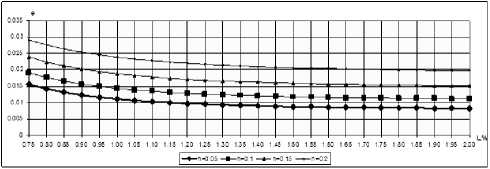
Рис. 4. Угол скоса потока при различных отстояниях при угле атаки a = 4 ° и удлинении X = 2

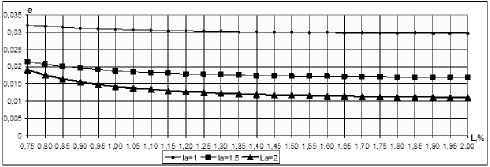
Рис. 5. Угол скоса потока при различном удлин е нии при угле атаки a = 4 ° и относительном отстоянии h = 0,1

Вследствие самоиндуцированного воздействия вихревая пелена обычно неустойчива и на некотором расстоянии от НП сворачивается в спираль. Важность представления вихревой пелены как распределения вихревых нитей состоит в том, что, используя конечный набор дискретных вихрей можно вполне адекватно моделировать разнообразные течения, в том числе и процесс сворачивания вихревой пелены. В отличие от бесконечно тонкой вихревой нити более приближенной к реальности [3] является модель цилиндрического вихря с конечным ядром круглого сечения радиуса r , в котором завихренность ю постоянна. Вне ядра течение полагается безвихревым. Для определения параметров вихря применена вихревая модель Ренкина, как одна из наиболее простых моделей, отражающая основные особенности концентрированных вихрей.

В работах [3] и [4] рассмотрен плоский ламинарный след за пластиной, расположенной параллельно потоку несжимаемой жидкости. Определено изменение полуширины следа и убывание дефекта скорости вниз по потоку. Дефект скорости

A u убывает по закону A u = U _о (4 x / r + 1)^-1/2, а полуширина следа нарастает по закону r = b [0,693 1 (4 x / b + 1)Re]^1/2. Ось x направлена вниз по потоку, а ось y – поперек; начало координат – на задней кромке НП.

В первом приближении принято, что ввиду небольших углов атаки передней НП при наличии экрана спутный след за ней практически прямолинеен. Данное упрощение при-

нято только для определения ширины следа для существенных отстояний при небольших углах атаки и неприменимо

при малых отстояниях, где ширина следа уменьшается за счет поджатия сходящих вихрей опорной поверхностью.

Так как полуширина следа есть условный радиус, то профиль давлений в ядре вихря на некотором расстоянии

зуется безотрывное обтекание (чем, собственно и обусловлено применение отклоняемого носка крыла). Таким образом, представляется целесообразным обеспечить безударное обтекание задней НП, что позволит, в свою очередь, улучшить ее аэродинамическое качество.

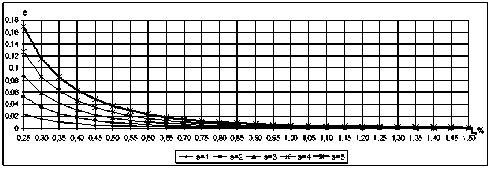
Рис. 7. Угол отклонения потока п ри различных углах атаки при относительном отстоянии h = 0,1 и удлинении X = 2

от вихря считается определенным.

Также рассмотрено поведение потока перед несущей поверхностью (рис. 6), для чего выполнено предположение о незначительности влияния свободных вихрей, сходящих с НП.

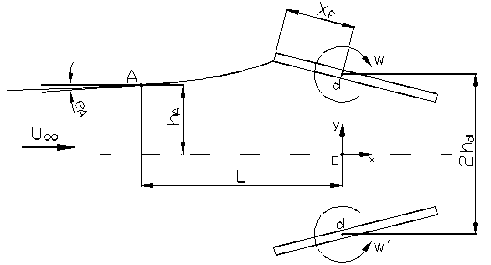
Рис. 6. Моделирование экрана для определения отклонения потока перед НП

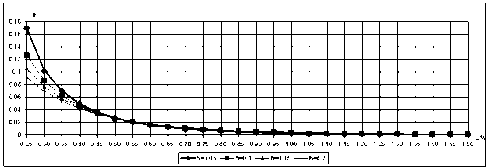
Рис. 8. Угол отклонения потока при различных отстояниях при угле атаки a = 4° и удлинении X = 2

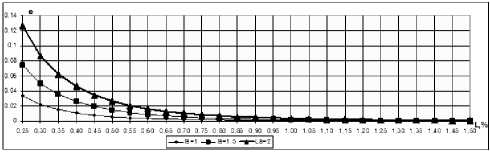
Рис. 9. Угол отклонения потока при различном удл и нении при угле атаки a = 4° и относительном отстоянии h = 0,1

Для определения угла отклонения потока перед НП расчетная формула принимает вид

cy

8 =—— К •

2пХ

X2                         )

^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^_  ^^^^^в

^4К У ^{L + (} h a ^- h d ) • ^4^ 2 ⁺ L ^{+ (} h a ^- h d )

X 2 У L + ( h a - h d ) 2

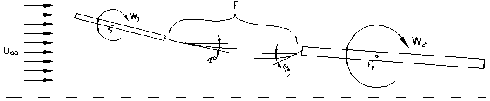
Рис. 10. Поток в межкрыльевой области

к ² 4 ( L² + ( h + h )²) •  ^Xy + L + ( h + h )^:

dada

V 4 к ²

Также методом максимальных приближений определена траектория потока перед НП для различных значений удлинения НП, угла атаки и отстояния от экрана.

По представленным графикам (рис. 7, 8, 9) видно, что при увеличении угла атаки НП угол скоса потока пропорционально увеличивается; при приближении НП к экра- ну угол скоса потока увеличивается; при увеличении удлинения НП угол скоса потока увеличивается, что полностью согласуется с реальной физикой явления. Кроме того, на расстоянии одной хорды от передней кромки НП по- ток условно можно принять горизонтальным ввиду малости значения угла отклонения потока.

Рассмотрено поведение потока в так называемой межкрыльевой зоне при обтекании комбинации несущих поверхностей как показано на рис. 10 (зона F ).

Для определения их рационального взаимного расположения подробнее рассмотрено обтекание носка задней НП.

Как известно [5], при безударном обтекании НП ее сопротивление существенно меньше притом, что реали-

Давление в критической точке А , где происходит расслоение потока, может быть представлено выражением

P a = P „ + q .

Сопротивление в данной точке максимально.

Для минимизации сопротивления использовано свойство вихревой пелены, сходящей с передней НП. Так как вихревая пелена характеризуется резким понижением давления, минимум которого наблюдается на оси вихря, то условие минимума давления в точке А запишется в виде

PAm „ = P™ + q , где Pmin – давление в центре вихря, сходящего с передней НП.

Физический смысл данной записи заключается в том, что точка А лежит на оси вихря, сходящего с передней НП. Именно при таком взаимном расположении НП поток, набегающий на среднюю поверхность, моделирующую профиль задней НП, не огибает переднюю кромку, а разделяется на ней на верхний и нижний. При этом такой режим обтекания возможен уже при различных уг- лах атаки задней НП, так как обеспечивается положением передней НП относительно задней НП. При данных условиях имеет место полная реализация подсасывающей силы и, как следствие, наименьшее аэродинамическое сопротивление НП.

Так как обтекание носка задней НП безударное, то в передней точке поток горизонтален ( ε ₂ = 0), то есть выполняется следующее условие:

c y 1                    c y 2

⁽ τ ^- τ экр1 ^{) =}       τ экр 2 ^,

λ ₁              2 λ ₂

где коэффициенты с индексом 1 характеризуют переднюю НП, а коэффициенты с индексом 2 характеризуют ных ранее условий не превышает половины толщины задней НП, а, следовательно, укладывается в область носка задней НП и оказывает влияние лишь на создание силы сопротивления.

Аэродинамическое качество задней НП рассчитыва- ется по формуле

K =

Cyρ ϑ2 Ky b, Kx∫(Pпер-Pзад)dx где Кх и Ку – коэффициенты интерференции сопротивления и подъемной силы соответственно:

заднюю НП.

В связи с вышеизложенным, принято, что определе- ние рациональных параметров взаимного расположения НП возможно при наличии такого начального условия, как h1 > (h2)0, где (h2)0 – отстояние носка задней НП от экрана.

Данным условием обеспечивается, собственно, возможность существования такой точи на вихревой пелене, в которой ε = 0 (поток горизонтален).

Угол скоса потока в межкрыльевой области с учетом интерференции имеет вид

где ϑ _возм и Р _возм – возмущенная скорость а давление соот-

ветственно.

Полный коэффициент интерференции НП:

K

инт

K y

K x

ϑ возм

P

P возм

.

ϑ

ε _i = ( ε ₁) _i - ( ε ₂) _{n - i} .

Пусть А – точка вихревой пелены, где ε = 0. Тогда:

Δ h = h_A - ( h ₂)₀.

Для приведения потока в носок задней НП описанные алгоритмы допускают множество вариаций:

( a ₁) _{i + 1} = ( a ₁) _i ^{( h A ) i} ;

h ₂

( h 1 ) i + 1 = ( h 1 ) i ^{( h A ) i} ;

h ₂

( L ) i + 1 = ( L ) i ^{( h A ) i} .

h ₂

Поиск решений ведется итеративно до получения удовлетворительной сходимости результатов.

Представленные алгоритмы позволяют определить искомое взаимное расположение НП, при котором может быть реализовано минимальное аэродинамическое сопротивление задней НП при относительно небольших потерях подъемной силы.

Вышеизложенные алгоритмы позволяют определять значение подьемной силы задней НП с учетом дефекта скорости, возникающим за передней НП. При этом, так как скорость в следе считается осредненной, то истинное значение скорости составляет среднее между рассчитанной в следе и скоростью невозмущенного потока. Изменение давления при определении подъемной силы не учтено, т. к. все значимые изменения укладываются в область ширины следа, что при выполнении поставлен-

Простота нахождения результата по изложенной методике позволяет рассмотреть в первом приближении большое число расчетных случаев за гораздо меньшее время с гораздо меньшими трудозатратами, при отсутствии необходимости в сложных измерительных комплексах и программных продуктах.

Кроме того, представленная методика применима для всего диапазона отстояний и не только для плоских НП, но и для телесных профилей, так как значения коэффициентов подъемной силы определяются вне данной методики (экспериментально, по атласу аэродинамических характеристик профилей, численными или иными методами).