Выбор упругих и геометрических параметров тонкостенной спицы зонтичной антенны

Большие развертываемые параболические антенны широко используются в системах спутниковой связи. Наибольшее распространение среди таких систем получили конструкции зонтичного типа с радиальными спицами-ребрами, соединенными одним концом с основанием (рис. 1).

Рис. 1. Радиальные спицы-ребра зонтичной антенны

К спицам с помощью вантовой системы крепится радиоотражающее сетеполотно. Зонтичная антенна в развернутом состоянии обладает значительными размерами, но перед установкой на космический аппарат она складывается в компактное стартовое положение (рис. 2).

В сложенном состоянии ребра касаются друг друга по всей длине. Это сделано для того, чтобы предотвратить биение и деформирование ребер на участке выведения, где сложенная антенна испытывает значительные перегрузки.

Спицы являются основными несущими элементами зонтичной антенны. Они должны обладать изгибной жесткостью, достаточной для раскрытия антенны и натяжения сетеполотна как при орбитальной эксплуатации, так и при наземных испытаниях конструкции.

Рис. 2. Стартовое положение спиц зонтичной антенны

Существует несколько подходов к конструктивному оформлению спиц зонтичной антенны [1...5]. Одной из перспективных конструкций спицы является тонкостенный стержень, состоящий из двух полуцилиндров и соединяющих их пластин (рис. 3).

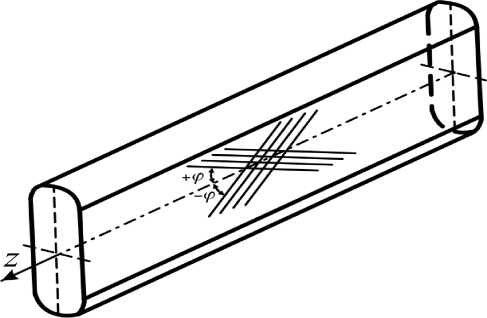
Рис. 3. Тонкостенная спица

Такой тонкостенный стержень изготавливается методом автоматической намотки, при котором лента композиционного материала укладывается на оправку под углом ± ф к образующей.

Решим задачу выбора упругих и геометрических параметров тонкостенной спицы зонтичной антенны, обеспечивающих требуемую изгибную жесткость конструкции.

Свяжем продольную ось спицы, проходящую через центры поперечных сечений с координатой z, отсчитываемой от основания (см. рис. 3) и отнесем поперечное сечение спицы к системе координатору (рис. 4).

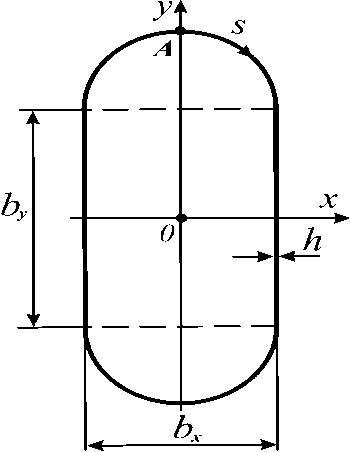
Рис. 4. Поперечное сечение спицы (обозначения см. в тексте)

Основными видами деформирования спицы являются изгиб в плоскости zoy и изгиб в плоскости zox . Изгиб в плоскости zoy происходит при нагружении спицы силами, возникающими в процессе натяжения сетеполотна, а изгиб спицы в плоскости zox - под действием силы тяжести при наземном кантовании антенны. Натяжение сетеполотна является основным расчетным случаем для спицы зонтичной антенны. Поэтому жесткость спицы при изгибе в плоскости zoy должна быть больше жесткости спицы при изгибе в плоскости zox.

Определим изгибные жесткости поперечного сечения рассматриваемой спицы. Обозначим через Ъ^ и Ъ_у размеры сечения вдоль осей x и у соответственно (см. рис. 4). Расчет тонкостенного стержня с замкнутым контуром поперечного сечения осуществляем на основе гипотез балочной теории [6], согласно которым поперечное сечение не деформируется и при изгибе поворачивается как жесткий диск. В рамках балочной теории изгибные жесткости поперечного сечения в плоскостях zoy и zox определяют следующим образом:

D x = J ^ВУ² ds D y = J Bx 2 ds , (1) где s - контурная координата, отсчитываемая от точкиИ; величина В обозначает жесткость стенки спицы при растяжении или сжатии в осевом направлении.

Стенка спицы состоит из большого числа тонких симметрично армированных (± ф ) слоев. Такую стенку можно считать однородной и ортотропной. В этом случае продольную жесткость определяем по формуле

B = ( An - A ²/ A 22 ) h , (2) где h - толщина стенки;

A 11 = E 1 cos⁴ ф + E ₂ sin⁴ ф + 2( Е 1 Ц 12 + 2 G 12 ) sin² ф cos² ф ;

A 12 = Е 1 ц ₁₂ + [ E 1 + E ₂ - 2( Е 1 ц ₁₂ + 2 С ₁₂)] sin² ф cos² ф ; (3)

A 22 = E 1 sin⁴ ф + E ₂ cos⁴ ф + 2( Е 1 ц ₁₂ + 2 C ₁₂)sin² ф cos² ф ;

которое сочетание этих параметров позволяет создать конструкцию, обладающую требуемыми жесткостями и минимальной массой.

Масса спицы может быть определена по формуле ms = рlh 2 пr(1 + - X),             (7)

π где / -длина спицы; р - плотность материала. Масса всех спиц m = nms,

где н - число спиц.

При реальном проектировании часть перечисленных выше параметров может быть вполне определена без решения общей оптимизационной задачи. В первую очередь это касается выбора материала и угла армирования. Анализ формул (3) показывает, что чем больше модуль упругости однонаправленного материала E_t и чем меньше угол армирования ф , тем большей жесткостью обладает поперечное сечение спицы зонтичной антенны. Поэтому из набора существующих материалов выбирают тот, у которого отношение E_t / р максимально. Как правило, таким материалом является углепластик.

Величина угла армирования определяется возможностями технологии намотки. При слишком малых углах намотки лента однонаправленного композиционного материала соскальзывает с оправки. Поэтому угол армирования, который может быть технологически реализован, как правило, не может быть меньше 15°.

Рассмотрим выбор параметров Ъ_х и Ъ_у, определяющих размеры поперечного сечения. Для этого воспользуемся тем обстоятельством, что значения изгибных жесткостей D_x и D_y , требуемых для раскрытия антенны, натяжения сетеполотна и кантования конструкции заданы. При известных D_x и D_y очевидно и их отношение n ⁼ D_x/ D_y.

Учитывая это, установим, как связаны между собой величины n и X . По уравнениям (5) будем иметь

E 2 ⁼

E 2 1 - µ ₁₂ µ ₂₁

E 1

; E i =;----------- ,

1 ^{- µ} 12 ^µ 21

здесь Е_р Е ₂ - модули упругости однонаправленного ком

позиционного материала вдоль и поперек волокон; G ₁₂ - модуль сдвига; ц ₁₂, ц ₂₁ - коэффициенты Пуассона.

Для стенки, чья продольная жесткость В не зависит от контурной координаты s, формулы (1) можно предста

1 + ⁸ λ+ 2 λ ² + ⁴ λ ³ η= ^π 3 ^{π η}

_{1 +} 4 _λ

.

вить в виде

D y = B J x² ds , D x = B J y ² ds .          (4)

Выполняя интегрирование по контуру поперечного сечения, будем иметь

D_x = n Br 3 (1 + ⁸ X + 2 X 2 + — X³ ), Dy = n Br 3 (1 + - X ) (5)

^x           π 3 π ^y           π

π

Представим равенство (9) в виде следующего полинома третьей степени:

4 . ,      . . 4

— X ³ + 2 X ² + -(2 -n ) X+ 1 -n = 0 .     (10)

3 ππ

где

b y

X=’

x

r = ^{b x} 2

.

Отметим, что при X = 0 ( Ъ_у = 0) рассматриваемое сечение превращается в круг.

Для выбранного материала, угла армирования ф , толщины стенки h и размеров сечения b_x, Ъ_у формулы (2), (3), (5) позволяют определить изгибные жесткости тонкостенной спицы зонтичной антенны. В общем случае не

Задавая различные значения n , для каждого из них можно найти три корня полинома. Установим диапазон изменения отношения изгибных жесткостей n в пределах от 1до 3. В этом диапазоне уравнение (10) имеет один вещественный положительный корень и два вещественных отрицательных корня. Значения интересующего нас положительного корня X для различных величин n приведены в табл. 1и на рис. 5.

Отметим, что используя метод наименьших квадратов, функцию X ( n ) можно представить в виде следующего аналитического выражения:

X = a ₀ + a 1 n + a ₂ n 2 + a ₃ n 3 , (11) где а₀- -0,905 49, а₁ - 1,064 57, а₂ - -0,1754 9, а₃ - 0,0176 3.

Таким образом, данные, приведенные в табл. 1 или формула (11) позволяют установить взаимосвязь между

заданным отношением изгибных жесткостей D_x и D_y и отношением подлежащих определению размеров попе

речного сечения b_x, b_y .

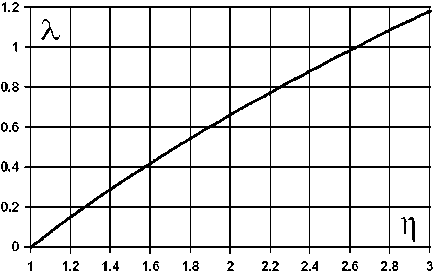
Рис. 5. Зависимость X^)

Покажем далее, что размер b_x может быть найден, если известен диаметр внутреннего пространства, образованного спицами в компактном стартовом положении (рис. 6).

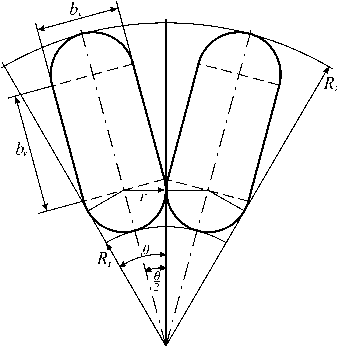
Рис. 6. Положение сечений спиц в собранном состоянии

Отметим, что величина радиусаR1 зависит в первую очередь от того, насколько компактно уложено сетепо-лотно во внутреннем пространстве, образованном спицами в стартовом положении.

При известном b второй размер поперечного сечения спицы b (см. рис. 4) может быть определен по выражению b y, = ^X b " .                        (14)

Напомним, что величина параметра X зависит только от заданного соотношения изгибных жесткостей спицы р . При рассматриваемом способе установки спиц в стартовом положении исходными данными для выбора b и b_y являются радиус внутреннего пространстваR₁, число спиц п и отношение изгибных жесткостей п .

Формулы (13), (14) и результаты решения уравнения (10) позволяют вычислить размеры b_x, b_y для любой ком-бинацииR₁, пи р .

При известных b_x , b_y можно определить радиус внешней окружности, внутри которой находятся спицы в собранном состоянии (см. рис. 6):

^R 2 = R i ^{+ b} x ⁺ b y .                (15)

Подставляя (13)и(14)в(15), окончательно получим

R 2 = R

• п sin

1 + 2(1 + X)----n- п

1 - sin — n

Определим далее массу спиц при найденных размерах поперечного сечения отдельной спицы. Подставим равенства (7) и (13) в формулу (8):

m = 2 п R 1 lh p f ,                 (17)

где

На самом деле по рис. 6 имеем

—r— = sin - , (12) r + R 1 2

где R ₁ - радиус внутренней окружности пространства, образованного спицами в собранном положении; с - центральный угол сектора, в котором расположено

п sin f = (1 + 2 X) n----n- •            (18)

^п     1 - sin ^П

n

Величина параметра/зависит от числа спиц п и от отношения изгибных жесткостей п (табл. 2).

Анализ формулы (17) и данных табл. 2 позволяет сделать выводы о влиянии различных параметров на массу набора спиц. Так, для выбранного материала масса будет тем меньше, чем меньше радиус свободного пространства между спицами R₁ и толщина стенки спицы п . Увеличение отношения изгибных жесткостей п приведет к увеличению мас

сечение спицы при соприкосновении с соседними сечениями спиц. Учитывая, что с = 2 п / п , по (12) будем иметь

сы спиц, а увеличение числа спиц п - к снижению массы.

. п sin r = b " = R----n-

2      1 - sin П

n

Таким образом, авторами решена задача выбора упругих и геометрических параметров тонкостенной спицы зонтичной антенны. Полученные результаты могут быть использованы при проектировании антенн для космических аппаратов.

Таблица 1

п	X	п	X	п	X
1,о	0,0	1,7	0,48342	2,4	0,88254
1,1	0,07680	1,8	0,54445	2,5	0,93497
1,2	0,15047	1,9	0,60398	2,6	0,98646
1,3	0,22142	2,0	0,66212	2,7	1,03705
1,4	0,28995	2,1	0,71896	2,8	1,08679
1,5	0,35633	2,2	0,77460	2,9	1,13572
1,6	0,42077	2,3	0,82910	3,0	1,18388

Таблица 2

п	№
	8	12	24	32
1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0	4,19 4,40 4,59 4,78 4,96 5,14 5,31 5,48 5,64 5,80 5,96 6,11 6,26 6,40 6,54 6,68 6,82 6,96 7,09 7,22 7,35	3,78 3,97 4,14 4,32 4,48 4,64 4,80 4,95 5,09 5,24 5,38 5,51 5,65 5,78 5,91 6,03 6,16 6,28 6,40 6,52 6,63	3,60 3,78 3,95 4,11 4,27 4,42 4,57 4,71 4,85 4,99 5,12 5,25 5,38 5,50 5,63 5,75 5,87 5,98 6,10 6,21 6,32	3,48 3,65 3,81 3,97 4,12 4,27 4,41 4,55 4,68 4,81 4,94 5,07 5,19 5,31 5,43 5,55 5,66 5,77 5,88 5,99 6,10