Выбор вариантов организации распределения запросов в системах предоставления информационных услуг

Развитие сферы услуг, в том числе информационного сервиса, сопровождается постоянным возрастанием требований к эффективности систем хранения обработки и передачи данных [1], одними из основных путей достижения высокой производительности, отказоустойчивости и надёжности которых являются кластеризация и динамическое распределение запросов [2 – 7].

Кластер представляет собой вычислительную систему, состоящую из нескольких связанных между собой компьютеров, используемых в результате диспетчеризации как единый, унифицированный компьютерный ресурс.

Обеспечение эффективности информационного сервиса требует выбора рациональных вариантов организации диспетчеризации запросов в распределенных системах, консолидирующих кластеры хранения и обработки информации.

Постановка задачи

Рассмотрим распределённую вычислительную систему, объ единяющую n серверов, m из которых реализуют функцию диспетчеризации. Запросы, приходящие в систему, попадают в один из серверов-диспетчеров (выбранный случайным образом), где случайно перераспределяются между серверами-исполнителями, выполняющими обработку запросов. При этом каждый сервер-диспетчер обрабатывает долю распределяемых им запросов g самостоятельно.

Ставится задача выбора вариантов организации распределения потока запросов между серверами кластера, при которых достигается минимум среднего времени пребывания запросов T в системе.

Оценка времени пребывания запросов в системе

Предположим, что поток запросов, поступающий в кластер, является простейшим, а длительности диспетчеризации, передачи дан- ных и обслуживания распределены по экспоненциальному закону. Исследуемую распределенную вычислительную систему представим сетью массового обслуживания, изображённой на рис. 1.

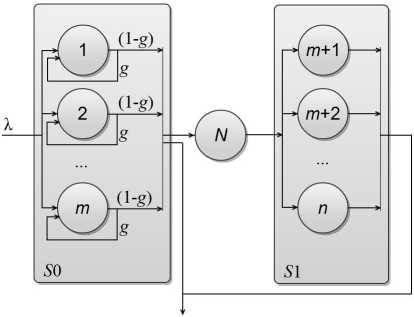
Рисунок 1. Модель массового обслуживания кластера

диспетчеризации при бесприоритетной ДО рассчитывается [8]:

_D _ ^д^  , ,

1    ,■ ХЬ .-b 0, где b0 — средняя длительность диспетчеризации запроса, b2 — средняя длительность обработки запроса.

При ДО с относительными и абсолютными приоритетами запросов на диспетчеризацию имеем:

d₂ = d₃ _ ^Хь2+дХ^ь2 + ь₀ .

• ^{2      3}     т-ХЬ₀     ⁰

Если запросы на обработку имеют относительный приоритет, то:

D 4 =

ХЬ2+дХЬ2

(1-^^(т-(ХЬ о +дХЬ 2 ))

+ й0.

В случае, когда запросы на обработку имеют абсолютный приоритет:

D s =

хь 2 +дхь 2

(1-^^(т-(ХЬ о +дХЬ 2 ))

д ^ХЬ2^ьо

+■ ”

Запросы, поступающие в группу серверов-диспетчеров S 0 с интенсивностью X, с вероятностью g обслуживаются в этих же серверах, а с вероятностью (1- g ) перераспределяются через сеть кластера ( N) на обработку в группу серверов-исполнителей S 1. Каждый сервер и сеть кластера представим одноканальными системами массового обслуживания (СМО).

Рассмотрим варианты организации распределения запросов, когда приоритеты запросов на диспетчеризацию и собственно решение функциональных задач одинаковы (бесприори-тетная дисциплина обслуживания, ДО); когда запросы на диспетчеризацию имеют относительный либо абсолютный приоритет над функциональными запросами и когда функциональные запросы имеют относительный либо абсолютный приоритет относительно задач диспетчеризации.

Среднее время пребывания запросов в системе вычисляется как:

T = D_tSQ ₊ (1^-_S№ ^{+ M}), ⁽¹⁾

где D — среднее время пребывания запроса в системе до окончания его диспетчеризации, Q — среднее время пребывания в системе запроса, обрабатываемого сервером-диспетчером, после окончания его диспетчеризации, L и М — среднее время пребывания перераспределённого запроса в сети кластера и в серв ер е-исполнител е соотв етств енно.

Для исследуемых вариантов организации распределения запросов среднее время пребывания запроса в системе до окончания его

Среднее время пребывания в системе

запроса,

обрабатываемого

сервером-

диспетчером, после окончания его диспетчеризации, при бесприоритетной ДО рассчитывается:

₉ _ Хь О +дХЬ₂²    , .

¹    m-(Хb о +gХb 2 )     ² ,

если реализуется ДО приоритетами запросов на то:

с относительными диспетчеризацию,

^{9 2} = (1

ХЬ2+дХЬ2

--^) ^{(т- (ХЬ} 0 ^+дХЬ2 ) )

+ ь2.

При ДО с абсолютными приоритетами запросов на диспетчеризацию имеем:

9 з =

ХЬ2+дХЬ2

(1 —~) ^(m- ( ^Хь о +д ^Хь2 ))

+ ^ + ^.

1 ^-ХЬ 0

В случае ДО с относительными или абсолютными приоритетами запросов на обработку:

9 4 = Q s _ ^дХт² + ^Й 2 .

т-дХЬ 2

Средние задержки перераспределённого запроса в сети кластера и в сервере-исполнителе получим на основе известной формулы для среднего времени пребывания запроса в СМО типа М / М /1 [8]:

L =---—--- М = —т"^²:—

L   1-(1-д)ХЬ1, M   1-1^2.’ где b 1 — средняя длительность передачи запроса по сети кластера.

Исследование проводится в условиях отсутствия в системе перегрузок:

^{ХЬо+дХЬ2} < 1, (1 - д)ХЬ_г<  1, ^^ < 1.

т               ¹       п-т

Выбор вариантов организации распределения запросов в системах предоставления информационных услуг

Выбор количества серверов-           запросов в системе является ДО с относитель- диспетчеров

Предположим, что n =10 шт., b 0 =0,2 с, b 1 =0,05 с, b 2 =1 с, g =0.1.

В результате расчётов, выполненных в системе математических расчетов Mathcad Prime 2.0, получены зависимости среднего времени пребывания запросов в системе от количества серверов, выполняющих функции диспетчеризации, представленные на рис. 2. На рис.2 кривые 1-5 соответствуют вариантам организации распределения запросов, когда приоритеты запросов на диспетчеризацию и собственно решение функциональных задач одинаковы; когда запросы на диспетчеризацию имеют относительный либо абсолютный приоритет над функциональными запросами и когда функциональные запросы имеют относительный либо абсолютный приоритет относительно задач диспетчеризации.

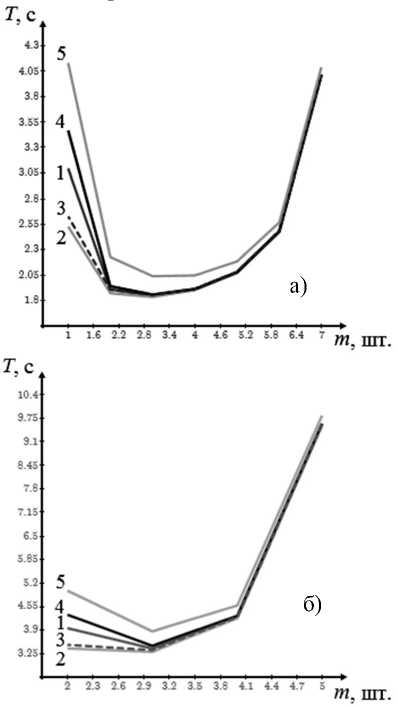
Рисунок 2. Количество серверов-диспетчеров: а) λ=2.5 1/с; б) λ=5 1/с

Из представленных графиков видно, что существует оптимальное количество серверов-диспетчеров, зависящее от ДО и интенсивности входного потока.

Наиболее эффективной с точки зрения минимального среднего времени пребывания ным приоритетом запросов на диспетчеризацию.

Выбор доли обрабатываемых серверами-диспетчерами запросов

В предположении, что m =3, получена зависимость среднего времени пребывания запросов в системе от доли обрабатываемых серверами-диспетчерами запросов, представленная на рис. 3. На рис.3 кривые 1-5 представляют варианты дисциплин диспетчеризации в порядке соответствующе предыдущему рисунку.

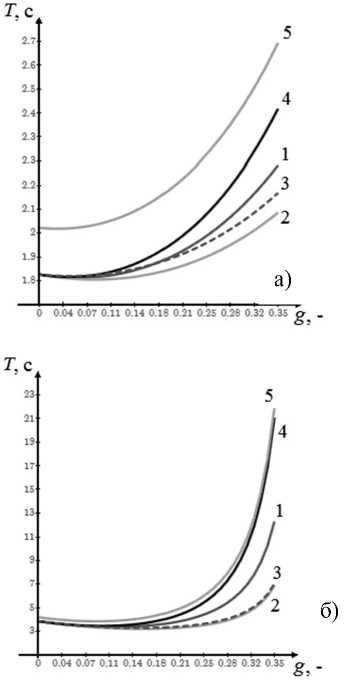
Рисунок 3. Доля обрабатываемых диспетчерами запросов: а) ^=2.5 1/с; б) ^=5 1/с

Из представленных графиков видно, что существует оптимальное значение g , зависящее от интенсивности входного потока.

Интенсивность потока может измеряться в реальном масштабе времени, в процессе функционирования исследуемой системы. Таким образом, задача оптимизации распределения запросов может решаться динамически. Измерение нагрузки замедляет работу системы, поэтому целесообразность адаптивной оптимизации требует обоснования.

Оптимизация распределения запросов

Поиск решения по оптимальному варианту распределения запросов проведем по критерию минимума среднего времени пребывания:

Т = mingT(m,s,A), где среднее время пребывания вычисляется на основании формулы (1).

В результате оптимизации находится количество серверов-диспетчеров m и доля запросов g , обрабатываемая в этих серверах, которые позволяют достичь минимума среднего времени пребывания запросов в системе.

Пров едём пример оптимизации распределения запросов для рассматриваемых ДО в серверах-диспетчерах при λ=5 1/c, n =10 шт., b 0 =0,35 c, b 1 =0,05 c, b 2 =1.

В результате расчётов установлено, что для бесприоритетной ДО оптимальным количеством диспетчеров является m 1 =3, а доля обрабатываемых ими запросов – g 1 =0.038, для ДО с относительными приоритетами запросов на диспетчеризацию – m 2 =10, g 2 =1, для ДО с абсолютными приоритетами запросов на диспетчеризацию – m 3 =3, g 3 =0.052, для ДО с относительными приоритетами запросов на обработку – m 4 =3, g 4 =0.03, для ДО с абсолютными приоритетами запросов на обработку - m 5 =3, g 5 =0.023.

Среднее время пребывания запросов в системе при указанных оптимальных значениях соответвенно равно: T 1 =4.312, T 2 =4.124, T 3 =4.34, T 4 =4.281, T 5 =4.495.

Заключение

Проанализировано влияние организации распределения запросов на эффективность вычислительного кластера информационного ceрвиca, показана эффективность разделения функций диспетчеризации между несколькими компьютерами кластера.

Показана эффективность организации в серверах-диспетчерах дисциплины обслуживания с относительным приоритетом запросов на диспетчеризацию над функциональными за-пpocaми.

Предложенные в статье рекомендации могут быть использованы при оптимизации дисциплин диспетчеризации и обслуживания запросов в системах распределенного предоставления информационного сервиса.