Выбор значимых факторов по результатам психологического эксперимента на примере исследования процесса измельчения листостебельной массы

Введение. При исследовании сложных процессов, в том числе характерных для сферы АПК, как правило, их рассматривают во взаимодействии множества факторов. Решение задачи по оптимизации или выбору их рациональных значений решают зачастую при недостаточном понимании «физики» этих явлений или процессов и не всегда поддающихся теоретическому описанию.

На практике для решения многочисленных задач моделирования различных предметных областей получили широкое распространение методы математической теории планирования многофакторного эксперимента [1–13]. Их реализация при экспериментальных исследованиях предполагает на основании изучения литературных источников, предварительных экспериментов, мысленного эксперимента, изучения объекта исследования находить совокупность факторов, определяющих искомый процесс (явление), в виде функционального соотношения

F = m* t , (i) где x i – факторы, определяющие искомый процесс; n – количество факторов.

Адекватность предполагаемой модели сложного процесса предусматривает использование только значимых факторов (параметров уравнения). Этот факт обуславливает временные и стоимостные затраты на организацию и проведение эксперимента, а также обработку экспериментальных данных. При этом возможно появление ошибок двух видов.

Первый вид ошибки – организация эксперимента с укороченным массивом значимых факторов. В этом случае «за бортом» могут оказаться факторы, которые оказывают значимое влияние на результирующий признак, а адекватность модели может подвергаться сомнению (особенно для значительного уровня доверительной вероятности при проверке нулевых гипотез).

Второй вид ошибки – включение в эксперимент значительного числа факторов, причем некоторые из них не являются значимыми. В этом случае возможны значительные затраты на организацию и проведение эксперимента, а в результате статистического анализа полученных экспериментальных данных выявится, что ряд факторов является незначимым и они не оказывают достаточного влияния на адекватность полученной модели.

Материалы и методы исследования. Вывод из указанного ранее следует такой, что при организации эксперимента для построения модели сложного процесса необходимо произвести предварительный анализ совокупности входных факторов и выявить множество факторов, являющихся значимыми.

Одним из возможных подходов решения указанной задачи является использование так называемого психологического эксперимента, основанного на методе экспертных оценок.

В результате осуществления анкетирования каждый специалист (эксперт), основываясь на своих знаниях, опыте, интуиции и т.п., указывает место каждого фактора в иерархии всех факторов от первого места до заключительного, равного их количеству. Ранговую оценку можно проводить, используя принцип «перевернутой шкалы» иерархии рангов. Это означает, что самому значимому фактору (номер 1) дают ранговую оценку, численно равную общему количеству из совокупности факторов с убыванием до наименее значимого, оцифрованного как 1.

Суммарную ранговую оценку каждого фактора представляют суммой его ранговых оценок у всех специалистов (экспертов).

Далее результаты такого ранжирования проверяют на согласованность мнений экспертов по критерию Кендалла (коэффициенту кон-кордации). Часто, как например в [1], делают вывод при значении коэффициента конкорда-ции, существенно отличающегося от нуля (между мнениями исследователей имеется достаточная согласованность [1, с. 58]), т.е. весьма неопределенно. Можно порекомендовать более точную оценку уровня согласованности мнений экспертов, основываясь на данных, приведенных в таблице 1.

Проверку нулевой гипотезы о значимости (не случайности) согласованности мнений экспертов определяют по критерию согласия Пирсона (χ ² ) [15]. При этом принята следующая градация лингвистической переменной – «уровень согласованности знаний экспертов»: согласованность слабая, умеренная высокая, очень высокая (рисунок 1).

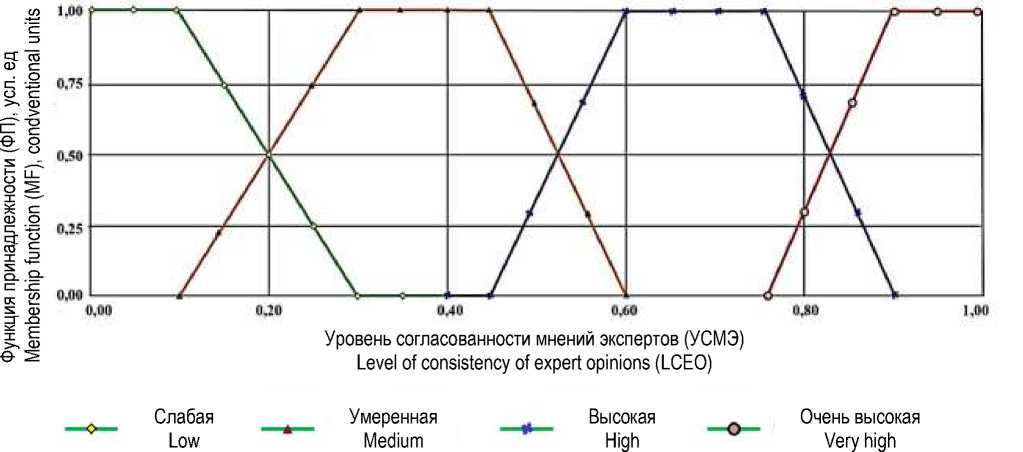
Рисунок 1 – Функция принадлежности (ФП) лингвистической переменной от «уровня согласованности мнений экспертов» (УСМЭ)

Figure 1 – Membership function (MF) of a linguistic variable from the «level of consistency of expert opinions» (LCEO)

После построения в порядке убывания суммарной диаграммы ранговой оценки факторов проводят оценку их значимости. В случае неравномерности убывания диаграммы при росте числа факторов (типа экспоненциального распределения) для дальнейшего исследования оставляют относительно небольшую часть так называемых «основных» факторов, но делают это, как например в [1], априори. Это может привести к тому, что из рассмотрения могут быть исключены весьма важные и значимые параметры и режимы.

Для придания обоснованного выбора анализируемых факторов для дальнейшего анализа можно использовать наработки, изложенные в [15, 16] и основанные на структуризации (выделение существенной, малосущественной и несущественной части) статистического массива значений идентификаторов.

Результаты исследования и их обсуждение. Для реализации этой задачи использовали данные психологического эксперимента по исследованию энергоемкости процесса измельчения листостебельной массы в молотковых дробилках агрегатов для приготовления витаминной травяной муки [1].

В результате анализа получили данные ранговой оценки факторов, влияющих на рассмотренный процесс (таблица).

Причем из дальнейшего рассмотрения авторы [1] исключили фактор x 1 , так как влажность листостебельной массы перерабатывают в дробилках в травяную муку в технологической цепи после сушильного агрегата, где эту массу доводят до относительной влажности 9–12% как в ГОСТ 18242-73 «Мука травяная», так и в настоящее время (ГОСТ 10242-2000 «Корма травяные искусственно выделенные»). Поэтому надо полагать, что авторы [3] включили фактор x 1 в рассмотрение (при всей его значимости) ошибочно, тогда как на самом деле он является ограничением.

Суммарная ранговая оценка факторов, определяющих энергоемкость процесса дробления листостебельной массы (по данным [1], с. 59, 60, 62, 63)

Total ranked assessment of factors determining the energy intensity of the process of crushing leaf and stem mass (according to [1], pр. 59, 60, 62, 63)

Обозначение Symbol	Фактор Factor	Уровень варьирования Range		Суммарная ранговая оценка, ед. Total ranked assessment, units
		нижний low	верхний high
1	2	3	4	5
х 1	Влажность измельчаемого материала, % Humidity of the crushed material, %	8	16	156
х 2	Окружная скорость молотков, м/с Peripheral speed of hammers, m/s	80	120	156
х 3	Степень измельчения материала Degree of material grinding	10	100	154
х 4	Диаметр отверстий, мм Hole diameter, mm	3	12	139
х 5	Коэффициент живого сечения решета Coefficient of sieve section	0,12	0,60	123
х 6	Подача материала в дробилку, кг/ч Material feed to the crusher, kg/h	300	800	116
х 7	Количество осей подвеса молотков, шт. Number of hammer suspension axles, pcs.	2	8	106
х 8	Количество молотков на молотковом поле ротора, шт. Number of hammers on the rotor hammer field, pcs.	16	48	105
х 9	Размер поверхности решета, град. Size of sieve surface, deg.	90	180	102
х 10	Рециркуляция крупной фракции при размоле Recirculation of coarse fraction during grinding	-	+	93
х 11	Крупность частиц сухой массы, мм Particle size of dry mass, mm	15	35	91
х 12	Форма отверстий решета Shape of sieve hole	круглая round	прямоугольная rectangular	90
х 13	Размер деки, град. Dize of deck, degrees	90	180	84

Окончание таблицы

1	2	3	4	5
х 14	Зазор между концами молотков и решетом, мм Gap between the ends of the hammers and the sieve, mm	5	45	78
х 15	Расход, воздуха: - минимум по всасыванию сечки; + максимум (по возможности) Air consumption: - minimum for chaff suction; + maximum (if possible)	–	+	73
х 16	Форма поверхности деки Shape of deck surface	контр. молотки rigid hammers	Рифленая Grooved	70
х 17	Толщина молотков, мм Hammer thickness, mm	2	10	70
х 18	Вентилирование дробилки (- воздушный поток не организован; + с организованным воздушным потоком по типу диаметрального вентилятора) Ventilation of the crusher (- the air flow is not organized; + with an organized air flow like a diametrical fan)	–	+	64
х 19	Форма концов молотков (- прямоугольные; + ступенчатые) Shape of hammer ends (- rectangular; + stepped)	–	+	60
х 20	Размер рифелей деки (высота), мм Size of deck riffles (height), mm	2	10	56
х 21	Диаметр камеры дробления, мм Siameter of crusher, mm	300	700	54
х 22	Место подачи материала в дробилку (- осевая, + тангенциальная) Place of material feed to the crusher (- axial, + tangential)	-	+	51
х 23	Плющение сухой сечки перед дроблением (- плющеная; + неплющеная) Flattening of dry chaff before crushing (- flattened; + unflattened)	-	+	37
х 24	Расположение патрубка отвода муки (- вертикальное; + наклонное под углом 45° против вращения ротора) Location of the flour outlet pipe (- vertical; + inclined at an angle of 45° against the rotor)	-	+	37
х 25	Наличие вентилирования большой деки Availability of large deck ventilation	-	+	34
х 26	Число молотков, проходящих по одному следу Number of hammers passing along one track	2	4	34
х 27	Значение установленной мощности электродвигателя (- малая; + большая) The value of the installed electric motor power (- small; + large)	–	+	34

Для снижения вероятности ошибок использовали специально разработанное программное обеспечение [17]. При структурировании статистического массива величин идентификаторов получили диаграмму интегральной функции F(x) накопленных частот доли значе- ний каждого фактора в общей совокупности (рисунок 2).

Так как ранговая оценка осуществлена в соответствии с частотой накопления, то резкое возрастание F(x) в начальный период перешло в относительно плавное протекание, приближаясь асимптотически на завершающем этапе к 1.

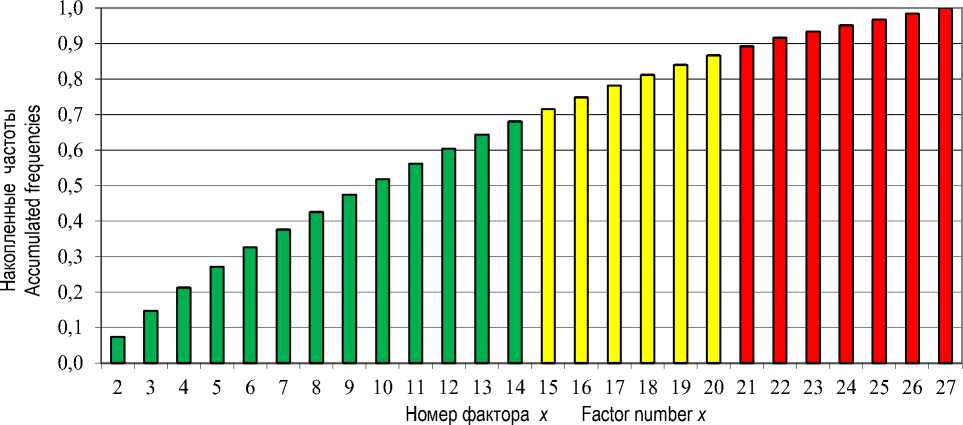
Рисунок 2 – Диаграмма интегральной функции F(x) накопленных частот доли значения каждого фактора в общей совокупности

Figure 2 – Diagram for the integral function F(x) of the accumulated frequencies of the share of the value of each factor in the totality

На рисунке 2 прямая линия характеризует средний темп формирования массива факторов в предположении, что каждый фактор вносит одинаковый вклад в общую совокупность, а ломаная линия выделяет три области. На рисунке четко прослеживаются три характерные области изменения функции F(x):

– там, где темп нарастания объема функции F(x) больше темпа нарастания объема факторов, формирующих этот объем;

– там, где темп нарастания F(x) примерно пропорционален темпу роста признаков;

– там, где темп нарастания F(x) меньше темпа увеличения признаков.

В соответствии с такой градацией все рассматриваемые факторы можно разделить на существенные (главные) – первая область, малосущественные – вторая область и несущественные – третья область

В результате установили, что к главным факторам, определяющим искомый процесс, можно отнести факторы (таблица) от х2 до х14, то есть 13 факторов, к малосущественным – от х15 до х20 и несущественным – от х21 до х27. В то же время в [1] отобрали только первые 9, произвольно предполагая [1, c. 61], что "... они наиболее сильно влияют на показатель энерго- емкости измельчения". Причем "Для дальнейшего исследования не был взят фактор х1 (важность исходного материала), так как величина его ограничена ГОСТом 18691-73" [1, с. 61]. Фактически оставили 8.

Таким образом, по данным исследований [1] не учли 38,5% главных факторов.

Выводы. Для объективного выделения количества значимых факторов, оставляемых после психологического эксперимента при реализации математической теории многофакторного эксперимента, использовали метод структуризации статистического массива, основанный на использовании интегральной функции накопленных частот доли значений каждого фактора в общей совокупности факторов.

На примере использования опубликованных ранее [1] результатов психологического эксперимента при исследовании процесса измельчения листостебельной массы в молотковых дробилках для приготовления витаминной муки установили, что главными факторами для дальнейших исследований должны быть как минимум 13 (со второго по четырнадцать включительно) [1] из таблицы, в то время, когда авторы опубликованной работы априори оставили 8, то есть не учли 38,5% главных факторов.