Вычисление геодезической высоты по прямоугольным пространственным координатам точек земной поверхности

Задача вычисления геодезической высоты Н определяемой точки Р по пространственным прямоугольным координатам X, Y, Z, измеренным с помощью спутниковых приемников, имеет широкие приложения.

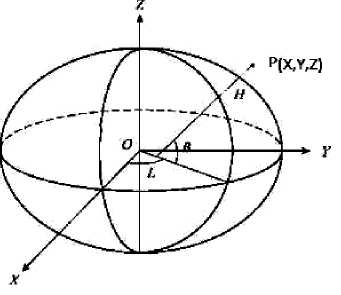
При решении главных геодезических задач в пространстве кроме геодезической высоты Н находят геодезическую широту В и геодезическую долготу L (рисунок) методом преобразований системы уравнений [1]:

X = ( N + H ) • cos B • cos L ;

< Y = ( N + H ) • cos B • sin L ;                 ⁽¹⁾

Z = [ N ( 1 - e ² ) + H ]• sin B ;

N =

a

V1 - e ² • sin² B

где N – радиус кривизны первого вертикала; е – первый эксцентриситет; a – большая полуось.

С помощью алгоритма высоты в работе [2] предлагается осуществить спутниковое нивелирование способом вычисления превышения Δ H = H 2 ‒ H 1 одной точки над другой. Такое нивелирование целесообразно использовать при трассировании железнодорожных путей, нефтегазопроводов и других протяженных объектов.

Для вычисления высоты применяют преимущественно алгоритмы

H = R / cos B - N ;       Н = Z / sin B - N (1 - e ²);       R = ^X² + Y² ,        (2)

по которым, как установлено в статье [3], при малой погрешности широты ДВ высота определяется с большой погрешностью.

Более стабильные по точности результаты получаются по формуле

Н = R • cos В + Z • sin В - а^1- е² • sin²B,                     (3)

погрешность которой оценивается по выражению [3]:

ДН = - 1 (а + ну ДВ² .

Однако для применения формул (2), (3) требуется предварительно вычислить геодезическую высоту В, что ведет к нерациональному пути решения задачи.

Результаты исследований

Чтобы получить алгоритм для прямого вычисления геодезической высоты Н по исходным координатам X, Y, Z, нужно в формуле (3) исключить функции широты В, как это выполнено в [4]. Только в качестве начального приближения возьмем более точную величину [5, с. 59]:

tg B о = Zc / R;    а₀ = ^R² + Z² / (1 - е²) ; c = 1 + ае² /( а ₀ ( 1 - е² )) ,         (5)

где ао - большая полуось вспомогательного эллипсоида, проходящего через точку Р (X, Y, Z) и имеющего одинаковый эксцентриситет с исходным эллипсоидом.

Погрешность формулы (3), вызванная неточной величиной широты В ₀ определяется по формуле (4). По начальному приближению (5) искомая широта В находится с погрешностью [5, c. 20]:

ДВ =

ае4Н

(а + Н)²

si'nB0cos3B0.

Подставляя (6) в (4), получим выражение для вычисления погрешности формулы (3) с начальным приближением (5):

ДН = -

а2е8Н2

2(-+Н)3•(sinBocos3вo)2■

В выражении (7) содержатся две функции Y1 = sinB • cos3B и v     а2н2

^Y 2 = ,,,■„< , которые

исследуем на экстремум.

Производная первой функции разлагается на множители Y{ = cos²B • (cos²B — 3sin²B).

Приравнивая эти множители к нулю, устанавливаем, что для функции Y 1 принимает наибольшее значение max Y 1 = 3^3/16 ~ 0,3248 на широте B = 30°.

Аналогично находим критические точки второй функции: Н = 0 и Н = 2a. Но при Н = 0 Y ₂ = 0, а при Н = 2a Y ₂ = 4a / 27.

Поэтому наибольшее значение погрешности (7) будет при Н = 2a и B = 30° и составит |ДH| = ae8/128 = 0,1 мм.

Однако для точек земной поверхности при |ДH| <10 ее погрешность не превосходит |ДH| < 0,0000016 мм = 1,6 • 10-6мм, что обеспечивает практически точный результат вычисления высоты.

Выведем теперь эту формулу для прямого вычисления высоты Н по исходным прямоугольным координатам X, Y, Z. Для этого с помощью выражения (5) tgB ₀ = Zc / R по тождествам cosB ₀ = 1/71 + tg²B₀ и sinB ₀ = tgB₀^cosB₀ определяем приближенные значения функции cosB и sinB , содержащиеся в уравнении (3).

Для удобства преобразований введем вспомогательные величины

D = 7R2 + (cZ)2;       R1 = R/D;       Z1 = Z/D.              (8)

Тогда

cosB0 = 1/71 + Z2c2/R2 = R/7R2 +Z2c2 = R/D = R1;

Zc

sinB0 = — = cZ1; ^1 — e2sin2B0 = 71- e2(cZ1)2

и формула (3) примет вид:

H = D(R2 + cZ12) — a71 —e2(cZ1)2 .                       (9)

Для предварительного вычисления точности и выбора вычислительной техники погрешность (7) формулы (9) выразим через исходные данные, полагая приближенно:

a + H = a0; a/(a + H) = a/a0;

H/(a + H) = a ₀ — 1;

sinB = Z/a0 ;      cosB = R/a0.

С этими обозначениями получаем:

ДH = — уй'

O- (ОНШ-®-

Закл ючение

Итак, по результатам исследований предлагается следующий алгоритм для вычисления геодезической высоты по пространственным прямоугольным координатам.

• 1)    R = 7^2 + Y2;

• 2)    a0=R71 + (Z/R)2/(1 — e2) ;

• 3)    c = 1 + ae2/(a0(1 — e2));

• 4)    D = R71 + (CZ/R)2;

• 5)    R1 = R / D; Z1 = Z / D;

• 6)    H = D(Rf + CZ-2) — a71 — e2(CZ1)2.

Для вычисления постоянных величин целесообразно использовать зависимости:

1 —e2 = ((/—1)//)2 ;       e2 = (2/ — 1)//2, где f - знаменатель сжатия a = 1 на эллипсоиде Красовского: f = 298,3; a = 6378245 м.

В геодезической системе координат 2011 г.: f = 298,2564151; а = 6378136,5 м.