Вычисление многомерных интегралов по криволинейным областям с гладкими границами
Автор: Шойнжуров Ц.Б., Санеева Л.И., Павлова Е.Б.
Журнал: Вестник Восточно-Сибирского государственного университета технологий и управления @vestnik-esstu
Рубрика: Естественные науки
Статья в выпуске: 2 (25), 2009 года.
Бесплатный доступ
В этой работе исследуются кубатурные формулы, содержащие значения функции с коэффициентами, зависящими от уравнения гладкой границы только в пограничном слое. Для решения данной проблемы был использован функционально-аналитический подход.
Кубатурные формулы, границы области, пограничный слой
Короткий адрес: https://sciup.org/142142089
IDR: 142142089 | УДК: 518.332
Calculation multivariate integral on curvilinear area with smooths border
n this work are researched cubatumye of the formula, containing importances of the function with factor, hanging from equation smooth borders in border layer only. For decision given problems was used function-analytical approach
Текст научной статьи Вычисление многомерных интегралов по криволинейным областям с гладкими границами
В данной работе построены кубатурные формулы с пограничным слоем на решетке с коэффициентами, зависящими от уравнения границы области только в пограничном слое.
Пусть j f (xdx - многомерный интеграл, у = ( y1, у2 ) и A'h^ - куб, сдвинутый на век-п тор hp и Ahe - криволинейный параллелограмм, Q - ограниченная область с гладкой границей Г =r(Q) на плоскости, начало координат (0,0) cQ, все пространство E2 и область Q де-k лятся на k частей, Q = U®., уравнение границы имеет вид x2 = Л(Х1) .
j = 1
Для разбиения единицы используем следующие многочлены [1]
Пусть ф ( 1 ) ( t ) =
' tm (1 -t) m, t g( 0,1), _ 0, t ^( 0,1), t1
^ (t) = j^ (tdT j^ (t)dT и ^(t) = ^ (2 + 21)• ^ (2-21).
Тогда ^ ( t ) G C ” , supp ^ ( t ) = [ - 1,1 ] ,
ф ( t ) = 1 при t < 1 и ^ ( t ) = Chm , C > 0, при | t | < Lh , L > 0. Разложение единицы в E n имеет следующий вид:
n _да_
n Z Ax - 3 A i=1 в^=-да l е 2
= 1, где е > 0.
Слагаемые, носители которых пересекаются с ® j , в сумме сгруппируем в отдельные функции ф . ( x ) , j = 1, 2, к , к . Если слагаемое попадает в несколько группировок, то относим его в какую-нибудь из них.
k
Пусть S j = SUpp Ф j ( x ) , to j cQ j и Q i= j = 1
k
Z Sj• j=1
Для каждой функции Ф j ( x ) , j = 1, 2, к , к построим свой функционал р ( x ) так, чтобы функционал l Q ( x ) с пограничным слоем получился по следующей формуле k
l Q ( x ) = Е ф ( x p j ( x ) .
j = 1
Рассмотрим построение кубатурной формулы на примере вычисления двойного интеграла
N
JJ f (x1,x2 ) = Z Ckf (xk), где Q {
Q к = 1
1, x 2 e E 2}.
Для построения кубатурных формул используется следующее разложение единицы: 1 = V 0 ( x ) + V 1 ( x ) , V x e E 1 = ( - да , + да ), где v 0 ( x ) = 1 - V 1 ( x ) V 1 ( x ) = v ( x ) и
V( x) = <
0, x < 0;
^2 m + 1 ) k ( 1 - 1 ) mdt , 0 < x < 1;
(m!)2 i
1, x > 1.
При m = 2 функция v ( x ) принимает вид:
I
v ( x ) = < 10 x 3 - 15 x 4 + 6 x 5,
1 = V 0
Графики ' x - 0,25'
I 1, функций v о ( x ) и V 1 ( x )
< x - 0.25 )
x < 0;
0 < x < 1
x > 1.
показаны на рисунке
1, где
0,5
+ Vil------
1 1 0.5
.
Построим разбиение области Q (рис.2) на : to 1 , а 2, to 3, ю 4. Рассмотрим финитные функции Ф 1 ( x ) , Ф 2 ( x ) , Ф 3 ( x ) , Ф 4 ( x ) , соответствующие разбиениям to 1 , ю 2, (У 3, to 4, и функцию 4
v(x), где x = (x1, x2) и Zфj = 1.
.j = 1
С помощью функции у ( x ) , полученной из формулы (1), при различных m получаем
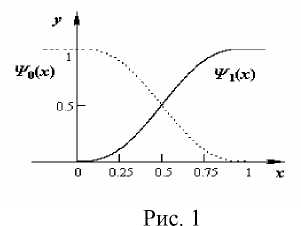
Разложение единицы
нужное разбиение единицы:
Ф i ( x 1 , x 2 ) = у
( x
V
е
a А
,
( x
Ф 2 ( x 1 , x 2 ) = у -1- 1 [ 1 — Ф з ( x 1 , x 2 ) — Ф 1 ( x 1 , x 2 )],
V е
Ф з ( x , , x 2) = у
(— x 2
—
a А
V е 7
,
[ 1 -Ф з ( x i , x 2 ) — Ф 1 ( x i , x 2 ) ], (5)
Ф 4( x 1 , x 2 ) = 1 — у -1
L V е где a - начало полосы, е - ширина полосы между областями.
Для области ю1 построим кубатурные формулы.
При замене переменных J У 2 x 2
—
М x 1 ) , криволинейные параллелограммы I переходят
l У 1 = x 1
в прямоугольники II (рис.3). Так как производим линейные преобразования, то финитная функция переходит снова в финитную функцию, решетка лежит в вершинах криволинейных параллелограммов.
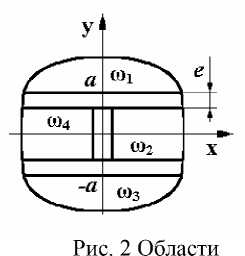
ю 1 , ® 2, <У 3, ® 4
Элементарный функционал погрешности для куба II имеет следующий вид:
Е Cy5(У1 — Y1 )Е CY 2 5( У 2 — Y 2),
m
m
Y 1 = 0
Y 2 = 0
где коэффициенты C Y и C Y определяются из систем
m
Е C y Y =--- -, a 0,1 = к , m , j 1,2 =
j a +1
Y j
В прямоугольнике II (рис.3) узлы на решетке заменяем узлами, лежащими на криволинейной решетке, сдвинутыми на дробную часть ^ ( h y ) = < ^( h Y 1 ) I Выполненные преобразования l h
проводились для определения коэффициентов Ks .
Построена вспомогательная формула для куба II с узлами в точках с крестиками.
Ф 1 (У) A (У ) =
Xi
-Ф1 (У) е< (У) —Е5(У1 — hY1 )ЕKY2 (Y1)5(У2 — hY2 + hn(hY1 ))h2 ,
Y 1
Y 2 = 0
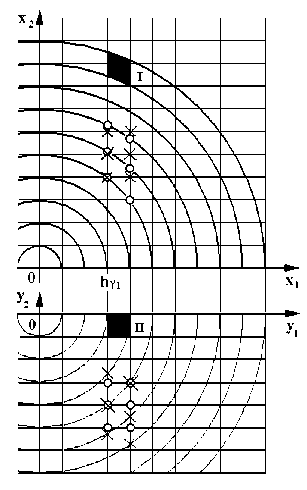
Рис. 3 Замена: < y 2 x 2 ^ ( X i ) , y i = x i
где
A he
.
min ( m , y 2 ) min ( m , y 2 - s )
Z K s ( Y i ) Z C r i, если 0 < Y 2 < m ,
K Y 2 ( Y 1 )=<
Теперь
= У 2 + 4У ) , x i = У
s = 0
m
Y i = 0
min ( m , y 2 - s )
Z Ks (/1) z
s = 0
Y i = 0
C Y , если 0 < у 2 < 2 m ,
1,
делаем
если у 2 > 2 m.
обратную
(9) замену
,
и криволинейный параллелограмм
переходит в куб A h p .
В формуле (5) переходим к переменным x :
ф1 (x) Pi (x ) =
to
= Ф 1 ( x ) M x ) - Z 5 ( x i - h P i ) Z К в 2 ( P i ) 5 x 2 - в
P i
в 2 = 0
-
Я ( h P i ) h
h
По формуле (10) вычисляется площадь параллелограмма с узлами, лежащими на решетке, а коэффи-
циенты зависят от уравнения границы. Это следует из построения вспомогательной кубатур-ной формулы в переменных у. Построена кубатурная формула для области ® 1. Для остальных областей основные формулы строятся аналогично.
В таблицах 1-4 показаны результаты вычисления интеграла с помощью формулы (10). Из таблиц видно, что при уменьшении шага h результаты улучшаются при различных параметрах m .
Зависимость погрешностей от параметра m для разных h a) h = 0.01, b ) h = 0.001, c ) h = 0.0001 b)
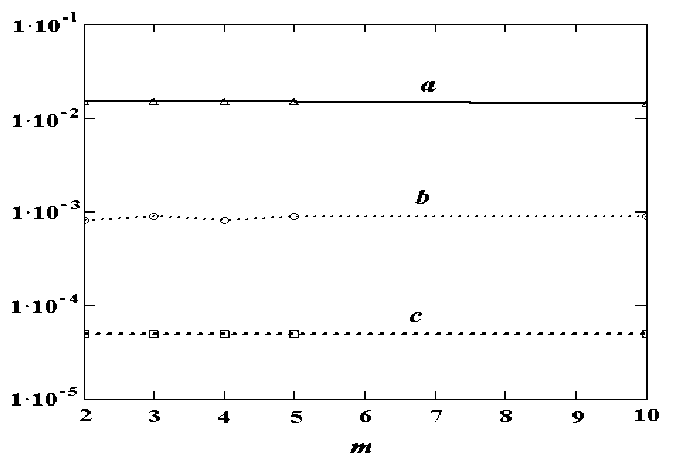
( x 2 + x 2 ) 2 4
Результаты вычисления интеграла I e dx 1 dx 2 , где □ область x T + x 2 < i .
n
.
|
m |
h |
а |
£ |
результат |
погрешность |
|
2 |
0,01 |
0,5 |
0,1 |
6,441 |
0,015 |
|
2 |
0,001 |
0,5 |
0,1 |
6,4545 |
0,0008 |
|
2 |
0,0001 |
0,5 |
0,1 |
6,45527 |
0,00005 |
|
3 |
0,01 |
0,5 |
0,1 |
6,441 |
0,015 |
|
3 |
0,001 |
0,5 |
0,1 |
6,4545 |
0,0009 |
|
3 |
0,0001 |
0,5 |
0,1 |
6,45527 |
0,00005 |
|
4 |
0,01 |
0,5 |
0,1 |
6,441 |
0,015 |
|
4 |
0,001 |
0,5 |
0,1 |
6,4545 |
0,0008 |
|
4 |
0,0001 |
0,5 |
0,1 |
6,45527 |
0,00005 |
|
5 |
0,01 |
0,5 |
0,1 |
6,441 |
0,015 |
|
5 |
0,001 . |
0,5 |
0,1 |
6,4545 |
0,0009 |
|
5 |
0,0001 |
0,5 |
0,1 |
6,45527 |
0,00005 |
|
10 |
0,01 |
0,5 |
0,1 |
6,441 |
0,014 |
|
10 |
0,001 |
0,5 |
0,1 |
6,4545 |
0,0009 |
|
10 |
0,0001 |
0,5 |
0,1 |
6,45527 |
0,00005 |
Точный результат – 6,45531727527116
Результаты вычисления интеграла J ( x 1 + x 2 dxxd dx 2 ), где Q область x 12 + x 4 < 1
n
Таблица 2
|
m |
h |
а |
£ |
результат |
погрешность |
|
2 |
0,01 |
0,5 |
0,1 |
1,952 |
0,005 |
|
2 |
0,001 |
0,5 |
0,1 |
1,9571 |
0,0003 |
|
2 |
0,0001 |
0,5 |
0,1 |
1,957376 |
0,000017 |
|
3 |
0,01 |
0,5 |
0,1 |
1,952 |
0,005 |
|
3 |
0,001 |
0,5 |
0,1 |
1,9571 |
0,0003 |
|
3 |
0,0001 |
0,5 |
0,1 |
1,957376 |
0,000017 |
|
4 |
0,01 |
0,5 |
0,1 |
1,952 |
0,005 |
|
4 |
0,001 |
0,5 |
0,1 |
1,9571 |
0,0003 |
|
4 |
0,0001 |
0,5 |
0,1 |
1,957376 |
0,000017 |
|
5 |
0,01 |
0,5 |
0,1 |
1,952 |
0,005 |
|
5 |
0,001 . |
0,5 |
0,1 |
1,9571 |
0,0003 |
|
5 |
0,0001 |
0,5 |
0,1 |
1,957376 |
0,000017 |
|
10 |
0,01 |
0,5 |
0,1 |
1,952 |
0,005 |
|
10 |
0,001 |
0,5 |
0,1 |
1,9571 |
0,0003 |
|
10 |
0,0001 |
0,5 |
0,1 |
1,957376 |
0,000017 |
Точный результат – 1,9573939495758
Результаты вычисления интеграла J e ( x 1 + x 2 ) dx 1 dx 2 , где □ круг x 12 + x 22 < 1 n
|
m |
h |
а |
£ |
результат |
погрешность |
|
2 |
0,1 |
0,5 |
0,1 |
5.53 |
-0.13 |
|
2 |
0,01 |
0,5 |
0,1 |
5.3995 |
-0.0013 |
|
2 |
0,001 |
0,5 |
0,1 |
5.39803 |
0.00011 |
|
2 |
0,0001 |
0,5 |
0,1 |
5.398139 |
0.000002 |
|
3 |
0,1 |
0,5 |
0,1 |
5.54 |
-0.14 |
|
3 |
0,01 |
0,5 |
0,1 |
5.3995 |
-0.0014 |
|
3 |
0,001 |
0,5 |
0,1 |
5.39803 |
0.00011 |
|
3 |
0,0001 |
0,5 |
0,1 |
5.398136 |
0.000006 |
|
4 |
0,1 |
0,5 |
0,1 |
5.58 |
-0.18 |
|
4 |
0,01 |
0,5 |
0,1 |
5.3995 |
-0.0013 |
|
4 |
0,001 |
0,5 |
0,1 |
5.39804 |
0.00011 |
|
4 |
0,0001 |
0,5 |
0,1 |
5.398136 |
0.000006 |
|
5 |
0,1 |
0,5 |
0,1 |
5.6 |
-0.2 |
|
5 |
0,001 |
0,5 |
0,1 |
5.39804 |
0.00011 |
|
5 |
0,0001 |
0,5 |
0,1 |
5.398136 |
0.000006 |
|
10 |
0,01 |
0,5 |
0,1 |
5.3962 |
0.0019 |
|
10 |
0,001 |
0,5 |
0,1 |
5.39804 |
0.00011 |
|
10 |
0,0001 |
0,5 |
0,1 |
5.398135 |
0.000006 |
|
Точный результат - п ( e - 1 ) « 5,39814156908377 f ( x2 + x 2 V] 1 2 Результаты вычисления интеграла 1 e ux 1u x 2 , где □ эллипс x L + x 2 < 1 a 4 2 |
|||||
Таблица 4
|
m |
h |
а |
£ |
результат |
погрешность |
|
2 |
0,01 |
0,5 |
0,1 |
37.487 |
0.005 |
|
2 |
0,001 |
0,5 |
0,1 |
37.4914 |
0.0014 |
|
2 |
0,0001 |
0,5 |
0,1 |
37.49284 |
0.00005 |
|
3 |
0,01 |
0,5 |
0,1 |
37.488 |
0.005 |
|
3 |
0,001 |
0,5 |
0,1 |
37.4914 |
0.0014 |
|
3 |
0,0001 |
0,5 |
0,1 |
37.49283 |
0.00006 |
|
4 |
0,01 |
0,5 |
0,1 |
37.487 |
0.006 |
|
4 |
0,001 |
0,5 |
0,1 |
37.4914 |
0.0014 |
|
4 |
0,0001 |
0,5 |
0,1 |
37.49284 |
0.00005 |
|
5 |
0,01 |
0,5 |
0,1 |
37.487 |
0.006 |
|
5 |
0,001 . |
0,5 |
0,1 |
37.4914 |
0.0014 |
|
5 |
0,0001 |
0,5 |
0,1 |
37.49284 |
0.00005 |
|
10 |
0,01 |
0,5 |
0,1 |
37.4916 |
0.0013 |
|
10 |
0,001 |
0,5 |
0,1 |
37.4914 |
0.0014 |
|
10 |
0,0001 |
0,5 |
0,1 |
37.49284 |
0.00005 |
Точный результат – 37,492890939765296285
